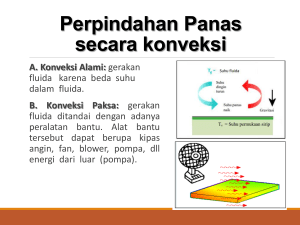
Perpindahan Panas secara konveksi A. Konveksi Alami: gerakan fluida karena beda suhu dalam fluida. B. Konveksi Paksa: gerakan fluida ditandai dengan adanya peralatan bantu. Alat bantu tersebut dapat berupa kipas angin, fan, blower, pompa, dll energi dari luar (pompa). Konveksi Alamiah Pada konveksi alamiah kita sering bertemu dengan bilangan tak berdimensi yang disebut angka Grashof (Gr). Konveksi Alamiah Rumus Empirik ALIRAN FLUIDA aliran laminer fluida bergerak menurut lapisan-lapisan tertentu dan tiap partikel mengikuti lintasan yang kontinyu. Tidak terjadi penyimpangan diantara garis aliran. aliran turbulen tiap-tiap partikel fluida bergerak tidak teratur, dengan mengakibatkan pertukaran momentum dari satu bagian fluida ke bagian yang lain. Turbulensi membangkitkan tegangan geser yang lebih besar di seluruh fluida & mengakibatkan kerugian. Bilangan Reynold Re merupakan rasio antara inertia force dengan viscous force. Bilangan ini digunakan untuk mengidentifikasi jenis aliran yang berbeda, seperti dari transisi ke laminar dan dari laminar ke turbulen tergantung pada geometri permukaan, kecepatan aliran bebas, suhu permukaan, kekasaran permukaan, kecepatan aliran bebas, suhu permukaan, jenis fluida, dan lain sebagainya. Bilangan Reynold 1. Pada aliran melintas di atas plat datar ρ.U .x U .x dan Re x μ ρ. U .L U .L ReL μ Re < 5 x 105, adalah jenis aliran laminer Re > 1 x 106, adalah jenis aliran turbulen Bilangan Reynold 2. Untuk aliran melintas silinder dan bola ρ.U .d U .d Re d μ Bilangan Reynold 3. Untuk aliran di dalam pipa ρ.Um.d Um.d Re d 4 .m Re d . d . 4 .Q Re d . d . Saluran bukan penampang lingkaran Utntuk penampang segiempat atau bentuk lain, pada saluran udara, pada penukar kalor dsb. 4.A dh Pw 4.h.b dh 2(h b) 2.h dh 1 ar dh = diameter hidraulik A = luasan penampang saluran Pw = keliling basah segiempat b = lbr dan h = tinggi, A = h . b dan Pw = 2 ( h + b ) ar = h/b, utk ar = 1, dh = h. 1/3 < ar < 3 ρ.Um.dh Um.dh Re d Red < 2000 laminer Red > 4000 turbulen Bilangan Nusselt (Nu) Bilangan Nu adalah bilangan tanpa dimensi yang menyatakan perbandingan perpindahan panas antara konveksi (h) konduktivitas termal fluida (k). 1. Pada aliran melintas plat datar, h .x Nu x k dan h .L NuL k koefisien terhadap Bilangan Nusselt (Nu) 2. Untuk aliran melintas silinder dan aliran dalam pipa h .d Nu d k x = jarak dari tepi depan L = panjang plat d = diameter dalam pipa, m h = koefisien perpindahan kalor konveksi, W/m2.K k = koefisien perpindahan kalor konduksi, W/m.K Aliran melintas di atas plat datar h.x Nu x k h .L NuL k 1. Untuk aliran laminer ( Re < 5 x 105 ) Untuk plat yang dipanaskan seluruhnya, 1/2 Nu x 0,332 Pr1/3 Re x Bila fluk kalor tetap: 1/2 1/3 0,453 Nu x Pr Re x Catatan: sifat pd Tf dan suhu dinding dijaga tetap Nilai koefisien perpindahan kalor rerata : h .L NuL 0,664 Pr1/3 Re x1/2 k 2. Untuk aliran turbulen ( Re > 1 x 106 ) Untuk plat yang dipanaskan seluruhnya, oleh Nusselt 0,8 1 NuL Pr 3 ( 0,037 ReL - 850 ) dengan ketentuan: 0,6 < Pr < 60 5 x 105 < Re < 108 Sedangkan Whitaker menyatakan bahwa: NuL 0,43 ( Re 0,8 0,036 Pr L - 9200 1/ 4 μ ) μw dengan ketentuan: sifat fluida dievaluasi pada suhu film Tf kecuali dan w 0,7 < Pr < 380 105 < Re < 5,5 x 106 Aliran melintasi penampang bukan lingkaran Bil. Nusselt n Nud C . Re d Pr 1/3 Bilangan Prandlt (Pr) Bil. Prandlt merupakan parameter yang menghubungkan ketebalan relatif antara lapis batas hidrodinamik dan lapis batas termal. Bil. Prandlt juga merupakan perbandingan antara difusi momentum dan diffusivitas kalor di dalam fluida.