Konsep Fisika Modern

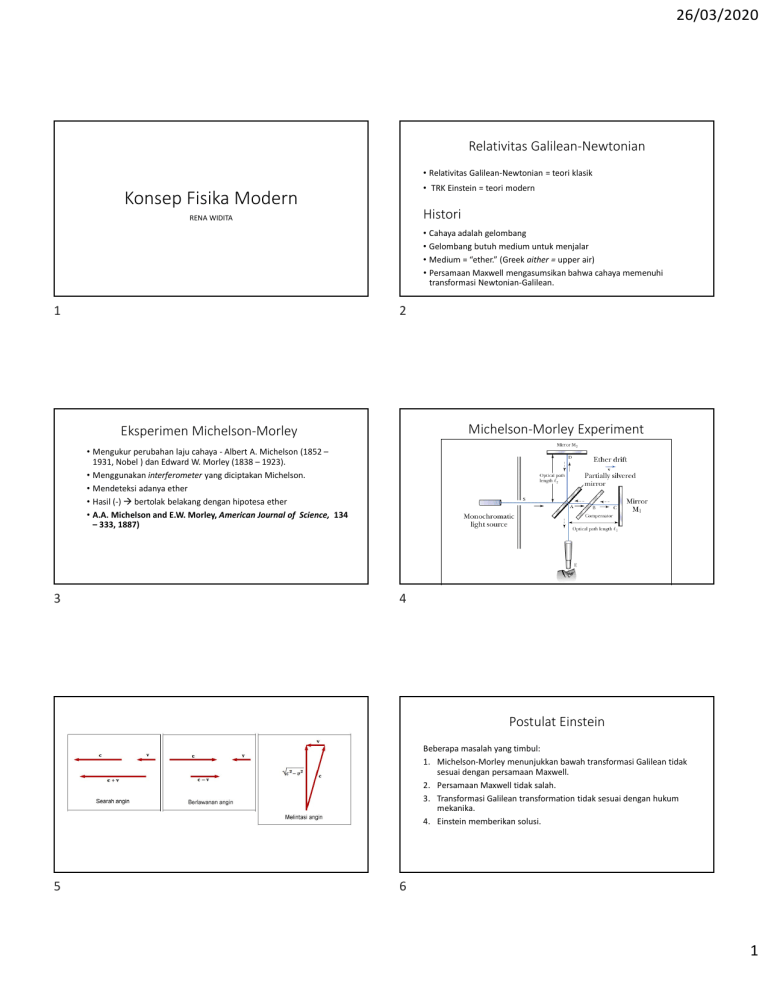
26/03/2020
Relativitas Galilean-Newtonian
• Relativitas Galilean-Newtonian = teori klasik
• TRK Einstein = teori modern
Konsep Fisika Modern
Histori
RENA WIDITA
• Cahaya adalah gelombang
• Gelombang butuh medium untuk menjalar
• Medium = “ether.” (Greek aither = upper air)
• Persamaan Maxwell mengasumsikan bahwa cahaya memenuhi
transformasi Newtonian-Galilean.
1
2
Michelson-Morley Experiment
Eksperimen Michelson-Morley
• Mengukur perubahan laju cahaya - Albert A. Michelson (1852 –
1931, Nobel ) dan Edward W. Morley (1838 – 1923).
• Menggunakan interferometer yang diciptakan Michelson.
• Mendeteksi adanya ether
• Hasil (-)  bertolak belakang dengan hipotesa ether
• A.A. Michelson and E.W. Morley, American Journal of Science, 134
– 333, 1887)
3
4
Postulat Einstein
Beberapa masalah yang timbul:
1. Michelson-Morley menunjukkan bawah transformasi Galilean tidak
sesuai dengan persamaan Maxwell.
2. Persamaan Maxwell tidak salah.
3. Transformasi Galilean transformation tidak sesuai dengan hukum
mekanika.
4. Einstein memberikan solusi.
5
6
1
26/03/2020
Kerangka Acuan Inersia
PRINSIP RELATIVITAS EINSTEIN
1. ‘Hukum-hukum fisika dapat dinyatakan dalam persamaan yang
berbentuk sama dalam semua kerangka acuan yang bergerak dengan
kecepatan tetap satu terhadap lainnya’
Kerangka yang
• Tidak ada percepatan jika tidak ada gaya luar
• Tidak dipercepat
• Hukum Newton berlaku pada semua kerangka inersia
 Tidak ada kerangka acuan yang universal.
2. ‘Kelajuan cahaya dalam ruang hampa sama besar untuk semua
pengamat, tidak bergantung dari keadaan gerak pengamat tsb’.
7
8
DILATASI WAKTU
a) Cahaya dikirimkan pengamat O’ yang diam
di dalam kereta ke kaca
b) Kaca dan pengamat O’ bergerak dengan laju
v relatif terhadap pengamat O yang diam di
luar kereta.
O mengukur lintasan yang dilalui cahaya > 2d.
Waktu yg diperlukan cahaya bergerak dari O’- cermin-O’:
∆t o =
2d
c
Untuk pengamat O, saat cahaya mencapai cermin, cermin telah bergerak ke
kanan sejauh v∆t/2, dimana ∆t adalah waktu yang diperlukan cahaya
bergerak dari O’ dan kembali ke O’.
2
2
 c ∆t   v ∆t 
2

 =
 +d
 2   2 
→ ∆t =
2d
c2 − v2
=
2d
c 1−
∆t =
v2
c2
∆to
1−
v2
c2
= γ∆t o
9
10
• Karena P2 mencapai bintang 2 dalam waktu ∆t0, ia menyimpulkan jarak antar
bintang:
∆t
L = v∆t o = v
RELATIVITAS PANJANG (KONTRAKSI PANJANG)
γ
• Kontraksi panjang merupakan konsekuensi dari dilatasi waktu
• Jarak antar 2 bintang tergantung dari kerangka acuan
Sedangkan panjang sebenarnya adalah L0 = v∆t, maka:
• Ada 2 pengamat : P1 di bumi
& P2 di pesawat
L=
• P1 mengukur jarak 2 bintang
L0  waktu yg dibutuhkan
pesawat untuk
menyelesaikan perjalanan ∆t
= L0/v
γ
= Lo 1 −
v2
c2
‘Jika sebuah benda mempunyai panjang sebenarnya Lo saat diukur oleh
pengamat yang diam terhadap benda, maka jika ia bergerak dengan kecepatan v
sejajar dengan panjangnya, maka panjang tersebut akan terukur lebih pendek’.
• P2 mengukur waktu tempuh
sebenarnya ∆t0 = ∆t/γ
11
Lo
12
2
26/03/2020
Seorang astronot menempuh perjalanan ke bintang yang jaraknya 8 thn
cahaya dari bumi. Ia mengukur waktu untuk 1 kali perjalanan 6 thn. Jika
pesawat bergerak dengan laju konstan 0.8c, berapakah waktu yang
diukur astronot tersebut?
Sebuah pesawat diukur panjang 120 m dan diameter 20 m saat diam
relatif terhadap seorang pengamat. Jika pesawat ini kemudian terbang
terhadap pengamat dengan kecepatan 0,99 c, berapakah panjang dan
diameter yang diukur pengamat tersebut?
L = Lo 1 −
v2
c2
= 120m 1 −
(0.99c )2
c2
Astronot melihat bintang mendekatinya, sehingga jarak sebenarnya akan menyusut
menjadi:
= 17m
8
γ
Diameter tetap (diameter adalah dimensi yang tegak lurus dengan
gerak, sedangkan kontraksi panjang terjadi hanya sepanjang arah
gerak).
= 8 1−
dan waktu tempuh diukur dengan jamnya adalah:
∆t =
13
v2
( 0. 8c )2
= 8 1−
= 5 thn chy
c2
c2
d
v
=
5
= 6thn
0. 8c
14
PERSAMAAN TRANSFORMASI LORENTZ
Pengamat di S (diam) melaporkan kejadian dalam
koordinat (x,y,z,t)
Pengamat di S’ (bergerak dengan laju v) melaporkan
kejadian dalam koordinat (x’,y’,z’,t’)
• Transformasi Galileo tidak berlaku jika v mendekati c.
• Persamaan yg berlaku untuk semua harga v (0≤v<c) adalah pers. Tranf. Lorentz:
x’ = γ(x – vt) ; y’ = y ; z’ = z ; t’ = γ(t – v.x/c2)
• Transformasi koordinat S’ menjadi koordinat S:
x = γ(x’ + vt) ; y = y’ ; z = z’ ; t = γ(t’ + v.x’/c2)
• Untuk v << c (v/c << 1 sehingga γ  1), persamaan ini menjadi persamaan Galileo
x’ = (x – vt) ; y’ = y ; z’ = z ; t’ = t
15
16
Jika obyek mempunyai kecepatan dalam komponen y dan z, maka komponen2 ini diukur
oleh pengamat S’:
PERSAMAAN TRANSFORMASI KECEPATAN LORENTZ
• Jika 2 pengamat yang saling bergerak relatif mengamati gerak suatu benda yg
kecepatannya mendekati c, anggap benda mempunyai komponen kecepatan ux’
terhadap kerangka S’:
′
′
′ =
=
−
→
=
−
→
= (
′ =
=
17
−
= (
(
(
−
′ =
)
−
−
1−
′ =
)
=
1−
′
′
−
)
′ =
)
)
(
′ =
′ =
=
(1 −
dan
1−
′ =
(
−
′ =
)
′
′
)
(1 −
=
1−
)
Transformasi dari kerangka S’ adalah:
−
=
−
′ +
′
1+
18
3
26/03/2020
Dua orang David dan Emily melakukan balap motor pada kecepatan
relativitas sepanjang jalur yang saling tegak lurus spt pd gbr. Seberapa cepat
Emily dilihat oleh David dari balik pundaknya?
Polisi (pengamat) berada di kerangka S, ia melihat:
David  ux = 0,75c dan uy = 0
Emily  ux = 0 dan uy = -0,99c
Untuk menghitung laju Emily dilihat oleh David, ambil S’ yang bergerak
bersama dengan David dan hitung ux’ dan uy’ untuk Emily.
u x '=
uy '=
u x −v
0 − 0. 75c
=
= −0. 75c
( 0 )( 0. 75c )
u xv
1−
c2
c2
1−
uy
γ  1 −

u '=
19
u xv 

c2 
=
(u x ')2 + (u y ')2
( 0. 75c )2
1−
(− 0. 9c )
2
c
( 0 )(
1−
=
0. 75c )
= −0. 6c
c2
(− 0. 75c )2 + (− 0. 6c )2 = 0. 96c
20
RELATIVITAS ENERGI
RELATIVITAS MOMENTUM LINIER DAN BENTUK RELATIVITAS
HUKUM NEWTON
Usaha yang dilakukan gaya ini:
=
⃗=
=
• Agar sesuai dengan postulat Einstein:
• momentum linier sistem terisolasi harus kekal untuk semua tumbukan
• harga relativitas
momentum linier harus mendekati harga klasik mu (dengan
Persamaan relativitas:
u mendekati nol)
⃗=
1−
⃗
⃗=
• Klasik: jika 2 partikel bertumbukan, momentum total pada sistem terisolasi dari
kedua partikel ini konstan.
=
=
1−
$
#
1−
=
/
=
=
!
/
1−
"
#
/
1−
=
=
1−
−
Konstanta mc2 tidak bergantung pada kecepatan partikel energi diam ER
E R = mc
Kembali ke persamaan klasik dengan u << c
21
2
γmc2 yang bergantung pada laju partikel  energi total E  penjumlahan energi kinetik dengan energi diam
Hubungan ini menunjukkan bahwa massa merupakan bentuk energi.
22
E = K + mc
E = mc = γmc
u
1−
c
2
2
2 pesawat A dan B bergerak dengan arah berlawanan spt pd gbr. Seorang
pengamat di bumi mengukur laju A 0.75c dan laju B 0.85c. Tentukan
kecepatan B oleh pengamat di dalam pesawat A.
2
2
2
Pada laju rendah, u/c << 1, dengan ekspansi binomial:
(1− β 2 ) 1/2 ≈ 1+ 1 β 2 + ... untuk
−
2
γ=
1
1−
u2
c2
 u2 
=  1 − 2 
 c 
−1/ 2
β << 1
1u2
≈ 1+
2c2

1u2   2 1
 − 1 mc = mu 2
K ≈  1 +
2 
2
 2 c  
→
ekspresi klasik
Dalam banyak situasi, lebih banyak digunakan ekspresi hubungan energi total E dengan
momentum linier relativistik p:
E
2
=
p c + (mc )
2 2
2 2
Pada keadaan diam maka p = 0  E = mc2
23
24
4
26/03/2020
Pengamat di bumi membuat pengukuran untuk kedua pesawat tersebut. Anggap
pengamat berada di S. Karena kecepatan B adalah yang ingin diukur, kita sebut lajunya
adalah ux = -0.85c. Kecepatan A adalah kecepatan pengamat tersebut terhadap kerangka
S’ ( v = 0.75c). Maka kecepatan B relatif terhadap A adalah:
Sebuah elektron bermassa 9,11x10-31 kg bergerak dengan laju 0,75c.
Tentukan momentum relativitasnya dan bandingkan harga ini dengan
momentum yang dihitung dengan cara klasik.
p =
me u
1−
( 9. 11x 10
v
2
c
2
=
−31
kg )(
8
3 x 10 m /s )
0. 75 )(
2
( 0. 75c )
1−
c
= 3. 10 x 10 −22 kgm /s
2
pklasik = meu = 2. 05 x 10 −22 kgm /s
Harga relativitas 50% lebih besar dibandingkan harga klasik.
ux '=
u x −v
− 0. 85c − 0. 75c
=
= −0. 977c
u xv
( −0. 85c )( 0. 75c )
1−
c2
c2
1−
25
26
Sebuah elektron di dalam tabung TV bergerak dengan kecepatan 0.25c.
Tentukan energi total dan energi kinetik elektron dalam eV (energi diam
elektron 0.511MeV).
a. Tentukan energi diam sebuah proton dalam eV jika diketahui massa
proton 1,67x10-27 kg.
b. Jika energi total sebuah proton 3 kali energi diamnya, berapakah laju
proton?
c. Tentukan energi kinetik proton dalam eV
d. Berapakah momentum proton?
m c = 0.511MeV = 0.528MeV
u 1−( 0.25c )
1−
c
c
K = E − m c = 0. 528MeV − 0. 511MeV = 0.017MeV
E
2
e
=
2
2
2
2
2
e
27
28
a.


1eV
 = 938MeV
E R = m p c 2 = (1.67 x10 − 27 kg )(3 x108 m / s )2 = 1.5 x10 −10 J 
 1.6 x10 −19 J 
2
b.
E = 3m p c 2 =
mp c
1−
→
1
3=
c2
1−
u2
c2
2
1
u
8
=
→
=
c2 9
c2 9
8
u=
c = 2.83 x10 8 m / s
3
1−
u
2
u2
c.
K = E − mp c 2 = 3m pc 2 − mp c 2 = 2m p c 2 = 1880MeV
d.
2
2
E 2 = p 2c 2 + m pc 2 = 3 m p c 2
(
(
p 2c 2 = 9 m p c 2
p= 8
mpc 2
c
) ( )
)2 − (mpc 2 )2 = 8(mpc 2 )2
= 2650MeV / c
Satuan momentum dalam MeV/c merupakan satuan yang umum digunakan dalam fisika partikel.
29
5