BAB II DASAR TEORI

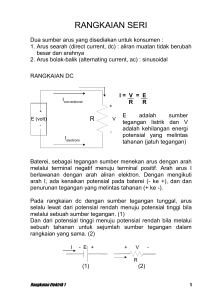
BAB II
DASAR TEORI
Beberapa kaidah dan konsep yang berlaku pada Eksplorasi Tahanan Jenis
(Taib, 1999 ) :
1. Kaidah Superposisi
Kaidah ini digunakan untuk menghilangkan kerancuan mengenai harga arus
listrik yang terjadi pada beberapa sumber arus listrik. Secara umum telah
disepakati bahwa arus listrik mengalir dari kutub positif (+) ke kutub negatif (-),
di mana besar arus listrik sama besarnya pada kedua kutub tersebut. Sehingga
apabila ada perbedaan ( ΔI ) maka digunakan perbedaan antara kedua sumber
tersebut.
2. Kaidah Resiprositas
Kaidah ini mengatakan bahwa potensial yang terukur dari suatu titik M akibat
dari suatu sumber arus pada titik A akan sama bila titik M tersebut menjadi
sumber arus dan titik A menjadi titik amat potensialnya.
3. Kaidah Potensial dan Arus Listrik
Medium homogen isotropik memiliki permukaan bidang isopotensial
berbentuk bola yang berpusat pada sumber arusnya, garis arus merupakan garis
radial tegak lurus terhadap garis isopotensial tadi. Untuk pasangan sumber arus
maka garis isopotensial ini akan menjadi lebih kompleks, namun tetap berbentuk
bola pada bidang dekat dengan sumber arus, sedangkan garis arus tetap tegak
lurus terhadap garis equipotensial tersebut. Namun untuk lapisan yang anisotropik
maka garis arus tidak harus selalu tegak lurus terhadap garis isopotensial tersebut.
6
4. Kaidah Kontroversi Kedalaman Penetrasi dan Resolusi
Kedalaman penetrasi akan bergantung kepada lebar jarak antara elektroda.
Semakin besar bentangan jarak elektroda maka akan semakin dalam penetrasi
yang diperoleh. Namun apabila semakin besar bentangan jarak antara elektroda
maka akan semakin kecil resolusi yang diperoleh.
5. Kaidah antara Tahanan Jenis dan Facies Batuan
Ada hubungan yang erat antara distribusi tahanan jenis batuan dengan
perubahan facies geologinya. Harga tahanan jenis biasanya akan mengalami
perubahan yang berangsur–angsur ke arah lateral, hal ini diakibatkan perubahan
porositas dan perubahan larutan pengisi. Perubahan facies geologi suatu Formasi
batuan biasanya merubah hubungan besar butir, porositas, dan salinitas larutan
pengisi pori yang terefleksi juga dari data tahanan jenis.
6. Kaidah Media Nonisometri
Eksplorasi tahanan jenis dilakukan dengan pendekatan media isometrik,
anomali dari media non isometri dipecahkan dengan menggunakan asumsi bahwa
perilaku tahanan jenis material bumi didekati dengan asumsi hubungan isotropi
dan anisotropi, homogen dan heterogen. Dengan demikian, pendekatan teori
tahanan jenis akan lebih mudah dikerjakan.
7. Media Isotropi dan Anisotropi
Secara definisi medium isotropi adalah medium yang memiliki harga tahanan
jenis yang sama untuk arah X, Y, Z. Sedangkan medium anisotropi adalah media
yang konduktivitas maupun harga tahanan jenisnya berubah pada arah tertentu,
umumnya ke arah pergerakan arus listrik. Grant dan West (1966) menyebutnya
sebagai medium Aelotropik.
8. Media Heterogen
Medium Heterogen Isotropi adalah suatu medium yang terdiri dari beberapa
gabungan media yang homogen isotropi yang berkontak dengan media homogen
isotropi lain dengan tahanan jenis ρ1, ρ 2, ρ3, dst. Kontak tersebut dapat berupa
7
kontak horizontal maupun vertikal, serta lensa yang secara keseluruhan
membentuk sifat heterogen untuk medium tersebut.
Metoda Tahanan Jenis merupakan suatu metoda yang bekerja dengan
mengukur beda potensial antara dua titik yang terjadi akibat adanya aliran arus searah
melalui bawah permukaan. Di mana tujuan dari metoda ini adalah untuk menemukan
distribusi arus yang melalui bawah permukaan yang berguna untuk melakukan
interpretasi terhadap material bumi. Pada dasarnya metoda ini mirip dengan sebuah
rangkaian listrik sederhana dengan sebuah baterai sebagai sumber tegangan dan
sebuah resistor sebagai hambatannya.
Gambar 2.1 Rangkaian listrik sederhana ( Burger, 1992 ).
Beda potensial pada ujung baterai menyebabkan muatan–muatan elektron
mengalir dari kutub positif ke kutup negatif. Pergerakan dari muatan–muatan elektron
melalui kabel perdetik itulah yang disebut arus.
I=
q
t
(1)
I adalah arus dalam ampere ( A ), q adalah banyak muatan dalam coulomb ( c
), dan t adalah waktu dalam detik ( s ).
Sedangkan besarnya arus yang mengalir pada suatu luas permukaan disebut sebagai
rapat arus ( J ) .
8
J=
I
A
(2)
di mana, J adalah rapat arus dan A adalah luas permukaan. Konsep dari rapat arus
sendiri memiliki peran yang besar dalam eksplorasi tahanan jenis. Dengan demikian,
apabila kita memperkecil luas permukaan potong pada besar arus mengalir yang
konstan, maka kita akan memperoleh rapat arus yang besar.
Hukum Ohm yang dikemukakan pertama kali oleh seorang fisikawan Jerman
yang bernama Georg Simon Ohm menyatakan bahwa Arus ( I ) berbanding lurus
dengan tegangan ( V ) dan berbanding terbalik dengan hambatan ( R ).
I=
V
R
(3)
Sebelumnya telah dikatakan bahwa arus adalah besarnya muatan yang
mengalir perdetik. Maka dapat dianalogikan seperti air yang mengalir melalui pipa.
Apabila pada salah satu ujung pipa kita beri kerikil maka ujung yang diberi kerikil
tersebut akan menghambat aliran air yang datang dari ujung yang bebas. Dengan
demikian dapat dikatakan jika hambatan pada sisi tersebut besar. Demikian juga jika
kita menambah panjang sisi pipa yang terisi oleh kerikil, maka hambatan akan lebih
besar dari sebelumnya. Namun apabila kita memperbesar diameter pipa maka
hambatan akan berkurang dan air mengalir lebih lancar. Maka dari analogi tersebut
dapat dinyatakan :
R=ρ
l
A
(4)
R adalah hambatan ( ohm ), ρ adalah hambatan jenis ( ohmmeter ), l adalah panjang
bahan ( m ), dan A adalah luar pemukaan bahan ( m² ).
9
Dengan anggapan bahwa setiap material geologi memiliki nilai tahanan jenis
yang berbeda–beda, maka dengan mengukur nilai besar arus yang mengalir dan nilai
beda potensial yang ada, dapat diketahui besar tahanan jenis yang ada pula. Dengan
demikian diharapkan dapat diketahui material geologi apa yang dilalui arus dan
terukur beda potensial antara dua elektroda potensial yang digunakan. Namun perlu
diingat bahwa tahanan tidak hanya bergantung pada material namun juga geometri
dari material tersebut seperti analogi yang telah dijabarkan di atas.
2.1
Sumber Arus Tunggal
Pendekatan yang digunakan dalam beberapa bahasan ke depan adalah
homogen isotropik. Dan arus mengalir di dalam bumi melalui material yang memiliki
besar hambatan jenis yang seragam dalam semua arah. Selain itu arus mengalir
seolah–olah membentuk bola di dalam bumi, di mana besar arus adalah sama pada
setiap arah dengan jari–jari ( jarak tempuh ) yang sama. Karena besar arus pada tiap–
tiap titik di permukaan bola adalah sama, di mana jarak dari elektroda arus C1 adalah
‘ r ’, maka besar potensialnya sama dengan pada permukaan tersebut. Permukaan ini
yang dinamakan permukaan equipotensial dan arah aliran arus akan tegak lurus
terhadap kontur equipotensial tersebut. Jika ditentukan tebal permukaan adalah ‘ dr ‘
lalu dengan persamaan 3 dan 4 , maka dapat ditentukan besarnya beda potensial pada
bagian ‘ dr ’ tersebut.
dr ⎞
⎛ l ⎞ ⎛
dV = i ( R) = i ⎜ ρ ⎟ = i ⎜ ρ
2 ⎟
⎝ A ⎠ ⎝ 2π r ⎠
(6)
Dengan persamaan di atas kita akan mencari besar potensial pada titik P1 dengan
jarak D dari titik C1, seperti yang diperlihatkan pada gambar berikut:
10
Gambar 2.2 Sumber arus tunggal dan elektroda potensial tunggal dengan D adalah
jarak keduanya, dan r adalah jari – jari bola , serta dr pemisah dua permukaan
potensial ( Burger, 1992 ).
Untuk menemukan besar potensial pada suatu titik maka akan dibandingkan
dengan potensial dengan sumber yang jauh sekali ( ∞ ), yang mana dapat dianggap
nol. Kemudian dengan mengintegralkan persamaan 6 sepanjang jarak D hingga
sumber arus pada jarak tak terhingga.
∞
V = ∫ dV =
D
i ρ ∞ dr
iρ
=
2
∫
2π D r
2π D
(7)
( Van Nostran & Cook, 1966, op. cit. Burger, 1992 ).
2.2
Sumber Arus Ganda dengan Satu Elektroda Potensial
Gambar 2.3 Elektroda arus ganda dengan satu elektroda potensial ( Burger, 1992 ).
11
Besarnya tegangan pada titik P1 akan dipengaruhi oleh dua sumber arus listrik
yang ada. Di mana arus mengalir dari elektroda arus positif ke elektroda arus negatif.
Hal ini telah dibuktikan oleh Franz Neuman pada tahun 1887. Jika P1 adalah titik
ukur potensial dan C1 (+) dengan C2 (-) masing–masing adalah sumber arus, maka
akan diperoleh hubungan sebagai berikut,
⎛ ρ ⎞ ⎛
ρ ⎞
V p1 = ⎜ i
⎟ + ⎜ −i
⎟
⎝ 2π r1 ⎠ ⎝ 2π r2 ⎠
(8)
Persamaan 8 di atas ditransformasikan ke system kordinat x-z maka diperoleh
persamaan :
⎧
⎫
⎪
⎪
⎪
⎪
iρ ⎪
1
1
⎪
Vp1 =
−
⎨
1
1 ⎬
2π ⎪
2
2
⎡ d
⎤ 2 ⎡⎛ d
⎤2 ⎪
⎞
2
⎪ ⎢⎛⎜ + x ⎞⎟ + z 2 ⎥
⎢⎜ − x ⎟ + z ⎥ ⎪
⎪⎩ ⎢⎣⎝ 2
⎠
⎠
⎥⎦
⎢⎣⎝ 2
⎥⎦ ⎪⎭
(9)
Karena arus mengalir tegak lurus terhadap kontur equipotensial maka ingin
diketahui bagaimana caranya arus mengalir pada bidang yang berlapis. Jika
dihubungkan kembali dengan prinsip elektronika tentang arus yang mengalir pada
rangkaian seri maka akan diketahui bahwa arus yang mengalir bukanlah arus total,
melainkan arus yang terbagi – bagi menjadi beberapa fraksi. Jika dimbil pendekatan
ini pada arus yang mengalir darielektroda C1 ( + ) ke elektroda C2 ( - ) maka akan
diperoleh fraksi arus sepanjang bidang vertikal yang ada di tengah sumber arus.
Apabila ‘ i f ’ adalah total arus, z adalah kedalaman, dan d adalah jarak pisah elektroda
maka total arus yang mengalir diberikan oleh persamaan,
12
if =
⎛ 2z ⎞
tan −1 ⎜ ⎟
π
⎝ d ⎠
2
( 10 )
(Van Nostrand & Cook, 1966, op. cit. Burger, 1992 ).
2.3
Sumber Arus Ganda dengan Dua Elektroda Potensial
Gambar 2.4 Sumber arus ganda dengan dua elektroda potensial ( Burger, 1992 ).
Beda potensial yang terukur adalah beda potensial yang terjadi antara dua
elektroda potensial yang dipasang di tengah–tengah dua elektroda arus. Dengan
mengaplikasikan persamaan 8 untuk masing–masing titik ukur potensial maka akan
diperoleh,
⎛ ρ ⎞ ⎛
ρ ⎞
V p1 = ⎜ i
⎟
⎟ + ⎜ −i
⎝ 2π r1 ⎠ ⎝ 2π r2 ⎠
( 11 )
⎛ ρ ⎞ ⎛
ρ ⎞
Vp 2 = ⎜ i
⎟ + ⎜ −i
⎟
⎝ 2π r3 ⎠ ⎝ 2π r4 ⎠
( 12 )
Dengan demikian maka beda potensial antara P2-P1 adalah :
13
⎛ iρ
iρ ⎞ ⎛ iρ
iρ ⎞
ΔV = V p1 − V p 2 = ⎜
−
−
⎟
⎟−⎜
⎝ 2π r1 2π r2 ⎠ ⎝ 2π r3 2π r4 ⎠
( 13 )
⎛1 1 1 1⎞
⎜ − − + ⎟
⎝ r1 r2 r3 r4 ⎠
( 14 )
⎛
⎞
⎜
⎟
2πΔV
1
⎟
⎜
ρ=
i ⎜1−1−1+1⎟
⎜r r r r ⎟
⎝ 1 2 3 4⎠
( 15 )
ΔV =
iρ
2π
Maka diperoleh besar ρ,
( Burger, 1992 ).
2.4
Faktor Geometri
Pada metoda Eksplorasi Tahanan Jenis ada beberapa konfigurasi elektroda
atau susunan elektroda arus dan potensial yang digunakan. Perbedaan letak elektroda
potensial ( M-N ) dari letak elektroda arus ( A-B ) akan memengaruhi besar medan
listrik yang diukur. Besar faktor oleh perbedaan akibat letak titik pengamatan disebut
faktor geometri ( K ).
⎛
⎜
1
K = 2π ⎜
1
1
⎜ − −1+1
⎜r r r r
⎝ 1 2 3 4
⎞
⎟
⎟
⎟
⎟
⎠
( 16 )
Masing–masing aturan atau konfigurasi elektroda memiliki nilai K yang tetap.
Berikut merupakan penurunan faktor geometri dari susunan elektroda Schlumberger,
14
bila AB/2 = r dan MN/2 = m dan menyubsitusikannya dengan persamaan 16 akan
diperoleh,
⎛
⎜
1
K = 2π ⎜
⎜ 1 − 1 − 1 + 1
⎝ AM BM AN BN
⎞
⎟
⎟
⎟
⎠
⎛
⎞
⎜
⎟
1
K = 2π ⎜
⎟
⎜ 1 − 1 − 1 + 1 ⎟
⎝ r−m r+m r+m r−m ⎠
⎛
⎞
⎜
⎟
1
K =π ⎜
⎟
⎜ 1 − 1 ⎟
⎝ r−m r+m ⎠
⎛
⎞
⎜
⎟
1
⎟
K =π ⎜
⎜ r +m−r+m ⎟
⎜ ( r + m) + ( r − m) ⎟
⎝
⎠
Ks =
π
(r
2m
2
− m2 )
( 17 )
jika ditulis dalam MN,
Ks =
π
2MN / 2
(r
2
− 1/ 4MN 2 )
⎡⎛ r ⎞ 2 1 ⎤
K s = π MN ⎢⎜
⎟ − ⎥
⎢⎣⎝ MN ⎠ 4 ⎥⎦
atau
⎡ r2
MN ⎤
−
Ks = π ⎢
⎥
4 ⎦
⎣ MN
15
untuk r >> MN maka dapat ditulis
⎛ r2 ⎞
Ks ≈ π ⎜
⎟
⎝ MN ⎠
( 18 )
Jika diketahui besar kuat medan listrik ( E ) adalah
E=
ρi
2π r 2
maka besar medan listrik akibat pengaruh dua sumber arus adalah
E=
ρi
x2
2π r 2
E=
ρ i dV
=
π r 2 dr
( 19 )
dan dengan substitusi persamaan 18 sebagai faktor geometri untuk AB/2 ( r ) >> MN
kedalam persamaan 15, maka diperoleh:
ρa =
π r2
iMN
ΔV
( 20 )
di mana dari persamaan 17 dan 18 kita dapat memperoleh syarat perbandingan AB/2
dengan MN,
e=
k − kt
x100%
kt
π r2
⎛ r2
MN ⎞
−π ⎜
−
⎟
MN
MN
4 ⎠
⎝
=
⎛ r2
MN ⎞
−
π⎜
⎟
4 ⎠
⎝ MN
=
MN 2
( 4r 2 − MN 2 )
16
MN =
4e 2
L
e +1
( 21 )
( Taib, 1999 ).
Persamaan 21 di atas merupakan pendekatan untuk bidang isopotensial yang
berupa bola. Dengan demikian dapat dilihat bahwa persamaan ini berlaku pada media
homogen isotropi. Namun persamaan 21 dapat membantu dalam perencanaan akuisisi
data.
Berikut beberapa faktor geometri untuk beberapa susunan elektroda (Loke,
2004) :
Gambar 2.5 Faktor geometri untuk beberapa susunan elektroda ( Loke, 2004 ) .
17
2.5
Tahanan Jenis Semu
Tahanan jenis semu merupakan tahanan jenis yang terukur di permukaan yang
dilakukan dengan aturan elektroda yang ada. Besarnya tahanan jenis yang terukur
tersebut merupakan besarnya tahanan jenis pengganti untuk variasi tahanan jenis yang
ada. Di mana asumsi dasarnya diturunkan dari medium homogen isotropik,
sedangkan pada kenyataannya medium yang terukur adalah medium anisotropik yang
tidak sesederhana asumsi awal. Adanya perbedaan antara hasil pengukuran dengan
harga tahanan jenis yang teoritis itulah yang disebut anomali. Selanjutnya anomali ini
yang akan membantu interpretasi besar tahanan jenis sebenarnya dan kedalaman yang
sebenarnya pula.
⎛
⎞
⎜
⎟
2πΔV
1
⎜
⎟
ρ=
i ⎜1−1−1+1⎟
⎜r r r r ⎟
⎝ 1 2 3 4⎠
Dari persamaan
( 22 )
2 dan 3 maka dapat dilihat hubungan bahwa potensial
berbanding lurus dengan rapat arus. Maka bila diukur besar potensial antara dua
elektroda potensial maka perubahannya akan sebanding dengan rapat arus pada
silinder dari material dekat permukaan yang berada antara dua elektroda potensial itu.
Hal ini akan memengaruhi besarnya tahanan jenis semu yang terukur. Pada gambar
3.6 dapat dilihat bahwa pada kasus ( a ) maka akan diperoleh harga ρa = ρ1. pada
kasus ( b ) rapat arus akan meningkat pada ρ2 > ρ1 sehingga ρa akan lebih besar dari
ρ1. Pada kasus ( c ) pada keadaan ρ2 < ρ1, rapat arus akan berkurang sehingga besar
ρa akan lebih kecil dari ρ1. Kesemuanya terjadi akibat pengaruh besar rapat arus yang
sebanding dengan besarnya beda potensial yang terukur.
18
Gambar 2.6 Efek tahanan jenis medium pada tahanan jenis semu yang terukur ( Burger, 1992 ).
2.6
Sifat Tahanan Jenis Batuan Berpori
2.6.1 Porositas dan Faktor Formasi
Porositas adalah bagian dari volume batuan yang tidak terisi oleh benda padat.
Ada beberapa macam porositas ( Harsono, 1997 ) :
1. Porositas Total, merupakan perbandingan antara ruang kosong ( pori2,
rekahan, retakan, gerohong ) total yang tidak diisi oleh benda padat yang
ada di antara elemen – elemen mineral dari batuan dengan volume total.
φt =
Vt − Vs V p
=
Vt
Vt
( 23 )
Di mana :
Vp = volume ruang “kosong”, biasanya terisi oleh fluida ( air, minyak, gas ).
Vs = volume yang terisi oleh zat.
Vt = volume total batuan.
φ = porositas.
Porositas total meliputi :
ƒ
Porositas Primer, antar butir atau kristal.
ƒ
Porositas Gerowong, diperoleh dari proses mekanik ( rekahan ) dan
dari proses kimiawi ( dolomitisasi ).
19
2. Porositas Bersambung ( connected porosity ), merupakan bagian dari ruang
kosong bersambung di dalam batuan. Contohnya batu apung.
3. Porositas Potensial, berhubungan dengan ukuran jalur pori – pori pada
batasan tertentu di mana fluida tak dapat lagi mengalir.
Pada formasi air bersih faktor formasi = 1, faktor formasi dinyatakan sebagai berikut :
F=
ρ0
ρw
di mana, ρ 0 = tahanan jenis total batuan.
ρ w = tahanan jenis air pengisi pori.
Pada batuan dengan butir dan porositas terisi air maka faktor formasinya berdasarkan
percobaan di laboratorium, adalah :
F=
a
φm
maka,
ρ0 = ρ w
a
φm
( 24 )
persamaan 24 dikenal sebagai hokum Archie I, di mana :
a = koefisien yang tergantung pada litologi, antara 0.6 – 2.
m = faktor sementasi yang tergantung dari jenis sedimen, bentuk pori, macam
sambungan pori, jenis pori, dan distribusi juga kemampatannya.
2.6.2 Kejenuhan
Kejenuhan adalah rasio dari volume yang terisi oleh cairan tersebut dengan
volume porositas total, ditandai dengan S ( Harsono, 1997 ).
Jika fluidanya adalah air formasi :
Sw =
Vw
Vp
di mana : Vw = volume terisi cairan.
20
Vp = volume porositas total.
Jika air adalah satu – satunya fluida yang mengisi pori maka Sw = 1, jika tidak maka :
Sw =
V p − Vw
Vp
Banyak percobaan laboratorium menunjukkan kejenuhan air dapat ditulis dalam
bentuk,
Sw =
ρ0
ρt
jika persamaan 24 di substitusi ke dalam persamaan di atas maka akan diperoleh :
ρt =
aρw
φ m S wn
( 25 )
persamaan 25 dikenal juga sebagai persamaan Archie II untuk formasi bersih, di
mana :
ρt = tahanan jenis batuan tidak jenuh air.
S w = kejenuhan air.
n = eksponen kejenuhan yang ditentukan berdasarkan percobaan.
2.7
Sifat Anisotropi Bahan
Suatu bahan dikatakan memiliki sifat anisotropi bila besar parameter
listriknya berubah terhadap arah, umumnya ke arah pergerakan arus. Menurut Kunetz
(1966), biasanya tahanan jenis dari suatu batuan bergantung terhadap arah dari arus
yang mengalir melalui batuan tersebut, dalam kasus ini batuan dikatakan bersifat
anisotropi. Sifat ini mungkin disebabkan oleh struktur mikro dari batuan tersebut.
Sebagai contoh batuan sedimen yang pada umumnya lebih resistan pada arah normal
terhadap bidang lapisan. Tahanan jenis ini mungkin diukur di laboratorium. Namun
untuk volume yang lebih besar pada saat pengukuran dalam eksplorasi, merupakan
21
suatu anisotropi semu. Dengan demikian, sifat anisotropi terkait dengan arah dan
skala yang digunakan.
Bardasarkan geometrinya maka sifat anisotropi tahanan jenis dibagi dua, yaitu:
1. Anisotropi makro yang meliputi sifat anisotropi akibat keadaan geologi,
seperti bidang lapisan, perubahan facies, struktur, dll.
2. Anisotropi mikro yang disebabkan oleh susunan kristal pembentuk batuan,
dan lainnya yang bersifat mikro yang terukur di laboratorium.
2.8
Pendekatan Anisotropi Dengan “Parameter Dar – Zarrouk”
Gambar 2.7 Ketebalan ( h ) dan tahanan jenis sebenarnya ( ρ) dari masing – masing lapisan. S
adalah total kondukatansi longitudinal dan T adalah total resistansi transversal ( Reynold, 1997 ).
Raymond Maillet ( 1947 ) berhasil memecahkan masalah media anisotropi
dengan suatu parameter yang dikenal dengan Dar–Zarrouk Parameter atau biasa
disebut Dar – Zarrouk Function. Nama ini diambil dari nama desa Kartago di Sidi
Bon Said, Tunisia. Inti dari parameter ini adalah pengertian tentang Unit Tahanan
Listrik Transversal ( ρt ) dan Unit Tahanan Listrik Longitudinal ( ρl ), terutama untuk
media homogen anisotropi. Media homogen anisotropi sendiri merupakan suatu
media dimana media tersebut homogen dan isotropi untuk masing–masing
lapisannya, atau bisa dikatakan kalau media homogen anisotropi merupakan media
22
yang terdiri dari lapisan–lapisan media yang homogen isotropi dengan sifat
kelistrikan yang berbeda antar lapisan, namun tetap untuk lapisan itu sendiri.
Sehingga dengan demikian perubahan terbesar terjadi pada arah vertikal terhadap
bidang lapisan. Itulah sebabnya akan selalu diperoleh nilai Tahanan Listrik
Transversal yang lebih besar dari Tahanan Listrik Longitudinal.
Harga Tahanan Jenis terukur dari suatu media merupakan resultan dari total
sifat fisik media tersebut, seperti Tahanan Listrik dengan arah tegak lurus bidang
lapisan ( ρt ) dan Tahanan Listrik dengan arah sejajar bidang Lapisan ( ρl ). Bila suatu
bidang lapisan dengan luas permukaan 1 m dan memiliki ketebalan t dan besar
tahanan jenis transversal untuk lapisan ke-i adalah,
Ri = ρi
l
A
untuk luas permukaan 1 m 2 dan l = h, maka,
Ri = ρi h
atau bisa ditulis dengan T adalah tahanan jenis transversal yang merupakan tahanan
jenis normal terhadap bidang perlapisan.
T = hρ
( 23 )
Sedangkan konduktansi yang sejajar dengan bidang perlapisan disebut dengan
konduktansi longitudinal ( S ).
S=
h
( 24 )
ρ
Maka dengan demikian dapat ditentukan besarnya tahanan jenis transversal dan
konduktansi longitudinal pada tiap lapisan ke-n,
n
T = ρ1h1 + ρ 2 h2 + ρ3 h3 + ... + ρ n hn = ∑ ρi hi
( 25 )
i =1
23
S=
2.9
h1
ρ1
+
h2
ρ2
+
h3
ρ3
+ ... +
hn
ρn
n
=∑
i =1
hi
( 26 )
ρi
Barnes Resistivity Layers
Pendekatan ini berdasarkan asumsi bahwa besar tahanan listrik yang terukur
merupakan tahanan listrik pengganti yang terbentuk dari tahanan listrik total.
Sehingga bila dikombinasikan dengan parameter Dar – Zarrouk, dapat diketahui
bahwa total tahanan jenis transversal untuk Dar – Zarrouk merupakan perhitungan
seri dari seluruh nilai tahanan jenis lapisan yang ada, sedangkan total konduktansi
longitudinalnya merupakan perhitungan paralel dari seluruh nilai tahanan jenis yang
ada.
ƒ
Konduktansi Longitudinal
Dengan menganggap bidang potensial berupa bola maka dapat dihitung
tahanan jenis untuk tiap lapisan h1, h2, h3, hn menggunakan parameter Dar–Zorrouk
apabila diketahui
a1 = h1, a2 = h1 + h2,...an = h1 + h2 + ... + hn , di mana a = kedalaman dan h = tebal
lapisan, maka dapat ditulis
S =∑
hi
ρi
Diturunkan dari Dar – Zarrouk untuk 2 lapisan,
S=
a2
ρa 2
=
h1
ρ1
+
h2
ρ2
apabila h2 = a2 − a1 , h1 = a1 , ρ a1 ≈ ρ1 , dan besar ρl = ρt untuk lapisan pertama,
maka
24
a2
ρa 2
h1
=
ρ1
ρl 2 =
+
( a2 − a1 )
ρl 2
a2 − a1
a2
a
− 1
ρa 2
ρ a1
atau dapat ditulis besar tahanan longitudinal untuk tiap lapisan ke – n adalah
ρl n =
an − an −1
an
a
− n −1
ρ an
ƒ
( 27 )
ρ an −1
Tahanan Jenis Transversal
Diturunkan dari Dar – Zarrouk,
T = ∑ hi ρi
maka untuk kasus 2 lapisan
T = a2 ρ a 2 = h1 ρ1 + h2 ρ 2
Dengan asumsi yang sama dengan di atas maka diperoleh,
T = a2 ρ a 2 = a1 ρ a1 + ( a2 − a1 ) ρt 2
ρt 2 =
a2 ρ a 2 − a1 ρ a1
( a2 − a1 )
Maka untuk tiap lapisan ke–n dapat dihitung besar tahanan jenis transversalnya,
ρtn =
an ρ an − an −1 ρ an −1
( an − an−1 )
( 28 )
Dengan diketahuinya besar masing–masing tahanan jenis baik pada arah tegak
lurus ( transversal ) maupun sejajar ( longitudinal ) dari masing–masing lapisan,
25
maka dapat ditentukan besar hambatan jenis anisotropinya ( ρ m ), di mana
merupakan resultan dari keduanya,
ρ m = ρl ρt
( 29 )
besar koefisien anisotropinya adalah
m = ρt / ρ l
( 30 )
Bila harga masing–masing tahanan untuk tiap lapisan diplot untuk tiap tengah
ketebalan masing–masing, maka akan didapat log “True Resistivity” dari Barnes
Resistivity Layers (Taib, 1999).
2.10
Teori inversi
2.10.1. Least Square Inversion
Metoda least square merupakan metoda inversi dari persamaan yang memiliki
jumlah data lebih banyak daripada parameter persamaan yang akan ditentukan. Pada
kasus seperti ini, solusi dari parameter yang dicari bukanlah merupakan hasil yang
eksak untuk semua parameter dalam persamaannya, melainkan hasil minimalisasi
jumlah kuadrat (sum of square) dari error (Manthey, 2001). Untuk itu maka data yang
digunakan haruslah data yang bersifat diskrit.
Metoda least square dapat dibagi menjadi dua jenis berdasarkan jenis
persamaannya, yaitu:
1. Linear Least Square
Persamaan simple linear adalah persamaan dimana parameternya bersifat
linear dalam bentuk,
n
di = ∑ Gij .m j
( 31 )
j =1
dan penyelesaian persamaan ini bersifat langsung dan sederhana.
2. Non-Linear Least Square
Persamaan
non-linear
adalah
persamaan
yang
parameternya
tidak
berhubungan langsung (linear) dengan hasil, seperti:
26
d = G.e −2 m
( 32 )
dan penyelesaiannya bersifat iterative dan lebih kompleks.
2.10.2. Metoda Gauss-Newton
Penyelesaian masalah inversi pada metoda ini didekati dengan fungsi
Gaussian. Di mana suatu persamaan nonlinear didekati dengan persamaan linear
dengan mengekspansi fungsi f (m) ke dalam deret Taylor disekitar model awal.
Model awal ini didasari oleh suatu nilai tebakan awal dengan variabel m0 . Persamaan
dari model awal dapat ditulis sebagai berikut ( Meju, 1994, op. cit. Gerald, 2006):
di0 = fi ( m10 , m20 , m30 ,..., mn0 )
( 33 )
Dengan asumsi bahwa f (m) bersifat linear di sekitar m0 , maka persamaan tersebut
dapat diekspansi dengan menggunakan deret Taylor,
m k +1 = m k + ( AT A) −1 AT y
⎧⎪ n ∂f (m0 )
⎫⎪
f ( m) = f ( m 0 ) + ⎨ ∑ i
.∂m j ⎬ + 0(|| ∂m ||2 )
⎩⎪ j =0 ∂m j
⎭⎪
( 34 )
Jika hubungan nilai observasi dengan hasil perhitungan dengan fungsi f (m) adalah:
d = f ( m) + e
( 35 )
di mana e adalah besar kesalahan ( error ), maka dengan menggunakan persamaan 35
dan 36 dapat diperoleh besar error, yaitu:
0
⎪⎧ n ∂f (m )
⎪⎫
e = d − f ( m) = d − f ( m 0 ) − ⎨ ∑ i
.∂m j ⎬
⎩⎪ j =0 ∂m j
⎭⎪
( 36 )
27
jika y = d − f (m0 ) , menunjukkan besar beda antara data observasi dengan hasil
perhitungan dan jika ∂fij / ∂m j = A , dan ∂m = x , maka dapat ditulis sebagai berikut:
e = y − Ax
( 37 )
Di mana A adalah turunan parsial dari f (m) terhadap variabel m yang berupa matrik
Jacobian. Karena matrik Jacobian bukan merupakan matrik yang simetris maka
fungsi yang akan diminimalisasi berupa:
q = eT .e = (d − f (m))T .(d − f (m))
q = ( y − Ax)T ( y − Ax)
( 38 )
Dengan menggunakan metoda Gauss-Newton maka persamaan nonlinear ini dapat
diselesaikan dengan menentukan turunan q terhadap x adalah 0:
∂q ∂ ( y T y − xT AT y − yT Ax + xT AT Ax)
=
=0
∂x j
∂x j
− AT y − yT A + AT Ax + xT AT A = 0
2 AT Ax − 2 AT y = 0
x = ( AT A) −1 AT y
( 39 )
x merupakan besar penambahan terhadap variabel awal yang akan selalu dicari untuk
tiap iterasi hingga besar x ≈ 0 . Jika ditulis dalam bentuk persamaan maka:
m k +1 = m k + ( AT A) −1 AT y
( 40 )
28
2.11
Kedalaman Penyelidikan pada Metoda Arus Searah ( Depth Of
Investigation )
Kedalaman penyelidikan (Depth Of Investigation ) merupakan kedalaman
dimana suatu lapisan tipis horizontal ( paralel dengan permukaan bumi ) memberikan
jumlah kontribusi maksimum terhadap total sinyal yang terukur pada permukaan
(Evjen, 1938). Depth of investigation ditentukan oleh posisi dari dua elektroda arus
dan elektroda potensial dan tidak hanya dari penetrasi arus maupun distribusinya
sendiri. Ada sebuah ide yang sudah menyebar luas, di mana untuk sumber arus dua
titik dengan spasi L pada susunan elektroda Wenner atau Schlumberger kedalaman
efektif adalah sama dengan L / 3 ≡ a ( Roy & Apparao, 1971 ). Avjen menemukan
bahwa kedalaman penyelidikan absolut pada susunan elektroda wenner bukanlah L/3
melainkan L/9. Akan tetapi kembali lagi, yang dimaksud dengan kedalaman
penyelidikan di sini bukanlah kedalaman dimana nilai tahanan jenis semu terukur
saja. Pada keadaan sebenarnya, nilai tahanan jenis semu yang terukur adalah
kontribusi (dipengaruhi) dari seluruh kedalaman, hanya saja dicari distribusi dari
besar kontribusi pada tiap kedalaman. Dengan demikian yang dimaksud dengan
kedalaman penyelidikan (depth of investigation) adalah kedalaman yang memberikan
kontribusi maksimum terhadap besar nilai tahanan jenis yang terukur dengan spasi
elektroda arus L tertentu yang kemudian disebut kedalaman absolut.
Dengan menggunakan kesamaan antara medan statis dan stasioner. Besarnya
perubahan medan potensial yang disebabkan oleh perubahan tahanan jenis dari suatu
lapisan tipis dapat diperoleh dengan mengasumsikan lapisan tipis horizontal tersebut
memiliki batas x dan y dari - ∞ sampai ∞ . Sehingga fungsi sensitivitas untuk lapisan
tersebut
pada
susunan
2
elektroda
sederhana
dapat
diperoleh
dengan
mengintegrasikan persamaan yang disebut Frechet Derivative dibawah terhadap x
dan y ( Loke, 2004 ).
F3 D ( x, y, z ) =
⎧
⎫
1 ⎪
x( x − a) + y 2 + z 2
⎪
⎬
1.5
1.5
2 ⎨
4π ⎪ ⎡ x 2 + y 2 + z 2 ⎤ ⎡ ( x − a ) 2 + y 2 + z 2 ⎤ ⎪
⎣
⎦
⎣
⎦
⎩
⎭
29
FID ( z ) =
1
4π 2
+∞ +∞
∫ ∫ ⎡x
−∞ −∞
⎣
x( x − a) + y 2 + z 2
2
1.5
1.5
+ y 2 + z 2 ⎤⎦ ⎡⎣( x − a) 2 + y 2 + z 2 ⎤⎦
dxdy
( 41 )
Persamaan diatas memiliki solusi yang sederhana ( Roy & Apparao, 1971, op.cit
Loke, 2004 ) berikut,
FID ( z ) =
2
z
π (a + 4 z )1.5
2
( 42 )
30
Nilai fungsi diatas kemudian diplot seperti yang ditunjukkan oleh gambar dibawah,
Plot Nilai Sensitivitas Untuk Tiap Z/L
Grafik kesensitifan untuk beberapa konfigurasi elektroda. Sumbu x adalah
perbandingan kedalaman dengan spasi elektroda arus (z/L) dan sumbu y adalah nilai
kesensitifannya, l = spasi elektroda potensial, dan L = Spasi elektroda arus.Panah
biru adalah kedalaman untuk sesitifitas maksimum Schlumberger array dan panah
jingga adalah nilai median depth of investigation Schlumberger array (Roy &
Apparao, 1971).
Beberapa penulis mengambil nilai maksimum dari grafik tersebut sebagai
kedalaman penyelidikan untuk masing–masing susunan elektroda. Namun Edward
(1977) dan Barker (1991) memberikan pendekatan dengan konsep Median Depth of
Investigation (Loke, 2004). Median Depth of Investigation adalah kedalaman di mana
area yang berada di bawah kurva sama besarnya dengan setengah dari total luas area
dibawah kurva. Dengan menggunakan konsep ini maka dapat didekati variasi
kedalaman dari masing–masing susunan elektroda.
31
A.Roy & Apparao, 1971 telah menemukan beberapa nilai maksimum dari
fungsi sensitivitas untuk beberapa susunan elektroda sebagai berikut :
Tabel 2.1 Besar perbandingan Depth of Investigation Characteristic terhadap spasi elektroda arus (
Roy & Apparao, 1971).
Two electrode
0.35L
Equitorial or azimunthal dipole( θ1 = π / 4 )
0.25L
Perpendicular dipole ( θ1 = π / 4 )
0.20L
Polar or radial dipole ( θ1 = π / 4 )
0.195L
Parallel dipole ( θ1 = π / 4 )
0.18L
Modified unipole
0.18L
Surface lateralog ( O1O2 = 0.1L )
0.17L
Surface lateralog ( O1O2 = 0.2 L)
0.135L
Schlumberger
0.125L
Wenner
0.11L
Di bawah ini merupakan besarnya perbandingan Median Depth of Investigation (Ze)
untuk susunan elektroda Wenner Schlumberger ( gambar 3.5.g ). Dimana L adalah
jarak antara elektroda arus ( AB ), a = 1, dan k adalah faktor geometri ( Loke, 2004 ) :
32
Tabel 2.2 Besar perbandingan Median Depth of Investigation terhadap spasi elektroda arus ( Loke,
2004 ).
Wenner Schlumberger
Ze/L
Faktor Geometri ( k )
n=1
0.173
6.2832
n=2
0.186
18.850
n=3
0.189
37.699
n=4
0.190
62.832
n=5
0.190
94.248
n=6
0.191
131.95
n=7
0.191
175.93
n=8
0.191
226.19
n=9
0.191
282.74
n = 10
0.191
345.58
Besarnya kedalaman dari penyelidikan berbanding terbalik dengan resolusi
vertikal yang didapatkan, jika diurutkan dari susunan elektroda dengan resolusi
vertikal terbesar hingga yang terkecil maka akan diperoleh :
1. Wenner
2. Schlumberger
3. Parallel dipole ( θ1 = π / 4 )
4. Polar ( radial dengan θ1 = π / 4 ) dipole
5. Perpendicular dipole ( θ1 = π / 4 )
6. Surface lateralog ( O1O2 = 0.2 L)
7. Surface lateralog ( O1O2 = 0.1L ) dan Modified unipole
8. Equatorial ( azimunthal dengan θ1 = π / 4 ) dipole
9. Two electrode
33