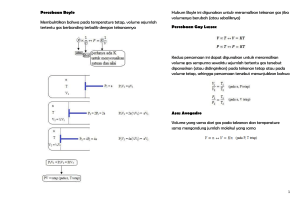
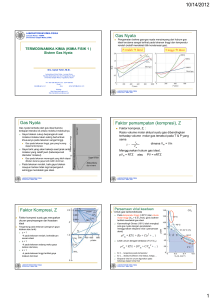
BAB I PENDAHULUAN 1.1 Latar Belakang Gas merupakan satu dari tiga wujud zat dan walaupun wujud ini merupakan bagian tak terpisahkan dari studi kimia, bab ini terutama hanya akan membahasa hubungan antara volume, temperatur dan tekanan baik dalam gas ideal maupun dalam gas nyata, dan teori kinetik molekular gas, dan tidak secara langsung kimia. Bahasan utamanya terutama tentang perubahan fisika, dan reaksi kimianya tidak didisuksikan. Namun, sifat fisik gas bergantung pada struktur molekul gasnya dan sifat kimia gas juga bergantung pada strukturnya. Perilaku gas yang ada sebagai molekul tunggal adalah contoh yang baik kebergantungan sifat makroskopik pada struktur mikroskopik. Maka dari itu semua jenis gas terbagi menjadi dua tipe, yaitu : gas ideal dan gas nyata. Gas ideal merupakan sebuah gas yang mematuhi persamaan gas umum dari PV = nRT yang disampaikan secara singkat, sedangkan gas nyata adalah gas yang tidak mematuhi persamaan gas umum dan menggunakan hukum-hukum gas hanya pada saat tekanan rendah. (Maron, Samuel Herbert : 5). Gas nyata (real gas) bersifat menyimpang dari gas ideal, terutama pada tekanan tinggi dan suhu rendah. Teori Kinetika gas menjelaskan Postulat 1: massa gas dapat diabaikan jika dibandingkan dengan volume bejana. Pada tekanan tinggi, atau jika jumlah molekul banyak, volume gas harus diperhitungkan à volume ideal sebetulnya lebih kecil dari volume real. Gas nyata hanya mengikuti persamaan gas ideal hanya pada suhu dan tekanan standar, sedangkan pada keadaan suhu dan tekanan tinggi, gas nyata tidak mengikuti persamaan gas`ideal. Kita dapat dengan mudah menentukan gas nyata harus dengan hipotesa gas, seperti semua gas mengandung molekul yang pasti menempati sebuah volum dan menggunakan saling tarik menarik satu sama lain. Bagaimanapun, faktor yang mempengaruhi menjadi diabaikan, dan kemungkinan tersebut ditinjau menjadi gas ideal. Kekuatan tarik antara molekul gas dianggap diabaikan. Asumsi ini hanya berlaku pada tekanan rendah dan suhu tinggi karena dalam kondisi molekul berjauhan. Tetapi pada tekanan tinggi dan suhu rendah volume gas kecil dan sehingga kekuatan menarik meskipun sangat kecil. 1 1.2 Rumusan Masalah 1.2.1 Apa itu gas nyata ? 1.2.2 Sifat-sifat gas nyata ? 1.2.3 Persamaan Van Der Walls ? 1.2.4 Apa itu Faktor Kompresibilitas ? 1.2.5 Apa itu Koefisien Virial ? 1.2.6 Apa itu Pengembunan ? 1.2.7 Apa itu Konstanta Kritis ? 1.2.8 Apa itu Asas Keadaan Yang Bersesuaian ? 1.2.9 Fugasitas Gas Nyata ? 1.3 Tujuan Penulisan 1.3.1 Untuk mengetahui apa itu gas nyata. 1.3.2 Untuk mengetahui sifat-sifat gas nyata. 1.3.3 Untuk mengetahui persamaan Van Der Walls. 1.3.4 Untuk mengetahui faktor kompresibilitas 1.3.5 Untuk mengetahui koefisien virial 1.3.6 Untuk mengetahui pengenmbunan 1.3.7 Untuk mengetahui konstanta kritis 1.3.8 Untuk mengetahui asas keadaan yang bersesuaian 1.3.9 Untuk mengetahui fugasitas gas nyata. 1.4 Manfaa Penulisan 1.4.1 Memeberikan informasi tentang gas nyata. 1.4.2 Memberikan informasi tentang sifat-sifat gas nyata. 1.4.3 Memberikan informasi tentang persamaan Van Der Walls. 1.4.4 Memberikan informasi tentang faktor kompresibilitas 1.4.5 Memberikan informasi tentang koefisien virial 1.4.6 Memberikan informasi tentang pengembunan 1.4.7 Memberikan informasi tentang konstanta kritis 1.4.8 Memberikan informasi tentang asas keadaan yang bersesuaian 1.4.9 Memberikan informasi tentang fugasitas gas nyata. 2 BAB II PEMBAHASAN 2.1 Pengertian Gas Nyata Gas merupakan suatu keadaan atau suatu bahan yang dapat dimanfaatkan serta mampu mengembang tanpa batas dan bebas bergerak sekehendaknya. Oleh karena itu tak berbentuk dan tak bervolume. Sangat bergantumg pada bentuk wadah yang ditempatinya. Gaya tarik menarik antara partikel-partikelnya kecil. Tumbukan dan hentakannya lemah. Atom-atom dan molekul-molekulnya senantiasa berseliweran dan berbenturan satu sama lain dengan dinding wadah yang didiaminya. Gas yang mengikuti hukum Boyle dan hukum Charles, yakni hukum gas ideal, disebut gas ideal. Namun, didapatkan, bahwa gas yang kita jumpai, yakni gas nyata, tidak secara ketat mengikuti hukum gas ideal. Semakin rendah tekanan gas pada temperatur tetap, semakin kecil deviasinya dari perilaku ideal. Semakin tinggi tekanan gas, atau dengan dengan kata lain, semakin kecil jarak intermolekulnya, semakin besar deviasinya. Paling tidak ada dua alasan yang menjelaskan hal ini. Peratama, definisi temperatur absolut didasarkan asumsi bahwa volume gas real sangat kecil sehingga bisa diabaikan. Molekul gas pasti memiliki volume nyata walaupun mungkin sangat kecil. Selain itu, ketika jarak antarmolekul semakin kecil, beberapa jenis interaksi antarmolekul akan muncul. Fisikawan Belanda Johannes Diderik van der Waals (1837-1923) mengusulkan persamaan keadaan gas nyata, yang dinyatakan sebagai persamaan keadaan van der Waals ataupersamaan van der Waals. Ia memodifikasi persamaan gas ideal (persamaaan 6.5) dengan cara sebagai berikut: dengan menambahkan koreksi pada P untuk mengkompensasi interaksi antarmolekul; mengurango dari suku V yang menjelaskan volume real molekul gas. Sehingga didapat: (P + a ) (V – b ) = R T V2 Atau P= RT (V – b) a (a.4 a) (a.4 b) V2 3 a dan b adalah nilai yang ditentukan secara eksperimen untuk setiap gas dan disebut dengan tetapan van der Waals (Tabel 6.1). Semakin kecil nilai a dan b menunjukkan bahwa perilaku gas semakin mendekati perilaku gas ideal. Besarnya nilai tetapan ini juga berhbungan denagn kemudahan gas tersebut dicairkan. Tabel 6.1g Nilai tetapan gas yang umum kita jumpai sehari-hari. gas a (atm dm6 mol-2) b (atm dm6 mol-2) He 0,0341 0,0237 Ne 0,2107 0,0171 H2 0,244 0,0266 NH3 4,17 0,0371 N2 1,39 0,0391 C2 H 4,47 0,0571 CO2 3,59 0,0427 H2O 5,46 0,0305 CO 1,49 0,0399 Hg 8,09 0,0170 O2 1,36 0,0318 Gas nyata bersifat tidak sempurna, yaitu gas yang tidak mematuhi dengan tepat hukum gas sempurnaa. Penyimpangan hukum terutama lebih terlihatpada tekanan tinggi dan temperatur rendah, khususnya pada saat gas akan mengembun menjadi cair. Kenyataan menunjukkan bahwa hukum gas ideal tidak dapat mendiskripsi sifat – sifat gas real secara tepat. Sebagai contoh adalah sebagai berikut : Jika kita mempunyai satu mol gas, berada pada ruang bertekanan 1 atm dan 0o C, menurut persamaan gas ideal, gas tersebut bervolume 22,4 liter. Tetapi kenyataan menunjukkan bahwa pada pengukuran sesungguhnya ternyata volume 1 mol gas pada 1 atm dan 0o C selalu lebih dari 22,4 liter. Di lain pihak, jika kita menpunyai 1 mol gas dari 0o C yang ditempatkan pada bejana bervolume 22,4 liter, ternyata tekanannya kurang dari 1 atm. 4 Dari kenyataan ini, maka tampak bahwa pada pengukuran gas sesungguhnya (real), diperoleh hasil pengukuran yang menyimpang formulasi persamaan keadaan yang lebih realistik dan menyelidiki implikasi persamaan keadaan tersebut. Gas Nyata Gas nyata berbeda dari gas ideal karena terdapat interaksi di antara molekulmolekulnya. Gaya tolakan cukup berpengaruh saat molekul-molekul akan saling bertumbuk khususnya pada tekanan sangat tinggi. Gas pada tekanan tinggi, gas yang kurang dapat terkompresi Gaya tarik yang akan bekerja saat jarak antar Interaksi Molekul Gas nyata memperlihatkan penyimpangan dari hukum gas sempurna karena molekul-molekulnya berinteraksi satu sama lain : gaya tolak antar molekul membantu pemuaian dan gaya tarik membantu penempatan. Gaya tolak antar molekul netral hanya bearti jika moleku-molekul tersebut hampir bersentuhan : gaya ini adalah interaksi jarak pendek, sekalipun dengan skala yang diukur dalam garis tengah (diameter) molekuler. Karena gaya itu adalah interaksi jarak pendek, tolak-menolak tidak boleh diabaikan hanya jika molekul-molekul tersebut secara rata-rata berdekatanaa. Ini adalah kasus pada tekanan tinggi, jika sejumlah besar molekul menempati volum yang kecil. Sebaliknya, gaya terik antar molekul mempunyai jereak relatif jauh dan gaya tarik itupun efektif diatas beberapa diameter molekuler. Gaya ini penting jika molekul-molekul cukup berdekatan tetapi tidak perlu bersentuhan. Gaya tarik menjadi tidak efektif jika molekul-molekul terpisah jauh. Dengan demikian, pada tekanan rendah, jika molekul-molekul menempati volume yang besar, pada sebagian besar waktu, molekul-molekul begitu jauh terpisah sehingga gaya antar molekul tidak mempunyai peranan bearti, dan gas berperilaku sempurna. Pada tekanan sedang, ketika molekul-molekul secara rata-rata hanya terpisah sejauh beberapa diameter molekuler, gaya tarik menang terhadap gaya tolak. Dalam hal ini, gas dapat diharapkan lebih mudah dimamfaatkan ketimbang gas sempurna. Temperatur dan tekanan kritis 5 Karena uap air mudah mengembun menjadi air, telah lama diharapkan bahwa semua gas dapat dicairkan bila didinginkan dan tekanan diberikan. Namun, ternyata bahwa ada gas yang tidak dapat dicairkan berapa besar tekanan diberikan bila gas berada di atas temperatur tertentu yang disebut temperatur kritis. Tekanan yang diperlukan untuk mencairkan gas pada temperatur kritis disebut dengan tekanan kritis, dan wujud materi pada temperatur dan tekanan kritis disebut dengan keadaan kritis. Temperatur kritis ditentukan oleh atraksi intermolekul antar molekul-molekul gas. Akibatnya temperatur kritis gas nonpolar biasanya rendah. Di atas nilai temperatur kritis, energi kinetik molekul gas jauh lebih besar dari atraksi intermolekular dan dengan demikian pencairan dapat terjadi. Tabel 6.2 Temperatur dan tekanan kritis beberapa gas yang umum dijumpai. Gas Temperatur kritis (K) Tekanan kritis (K) Gas Temperatur kritis (K) Tekanan kritis (atm) H2O 647,2 217,7 N2 126,1 33,5 HCl 224,4 81,6 NH3 405,6 111,5 O2 153,4 49,7 H2 33,3 12,8 Cl2 417 76,1 He 5,3 2,26 Koefisien Virial Pada volume besar dan temperatur tinggi, isoterm gas nyata dan isoterm gas sempurna tidak jauh berbeda. Perbedaan kecil ini menunjukkan bahwa hukum gas sempurna berlaku pada tekanan rendah dan pada kenyataannya merupakan suku pertama dalam pernyataan yang berbentuk. pVm = RT (1 + B’p + C’p . . .) Dalam banyak penerapan, deret yang lebih cocok adalah pVm = RT 1+B+C+... Vm Vm Pernyataan tersebut adalah dua versi dari persamaan keadaan virial (nama ini berasal dari kata latin untuk gaya). B, C, . . . , yang bergantung pada temperatur, adalah koefisien virial yng kedua, ketiga, . . . , koefisien virial yng ketiga C biasanya kurang penting ketimbang yang kedua B dalam arti bahwa volume molar khas C/Vm2 << B/Vm. Persamaan virial adalah contoh pertama dri prosedur umum dalam kimia fisika, dimana satu hukum sederhana (dalam hal ini pV = nRT) dianggap sebagai suku pertama deret pangkat satu variabel (dalam hal ini p atau Vm ). 6 Persamaan virial dapat digunakan untuk memeragakan suatu hal penting yaitu walaupun persamaan keadaan gas nyata dapat sama dengan gas sempurna sewaktu p 0, semua sifat-sifatnya tidak perlu sama dengan sifat-sifat gas sempurna. Perhatikanlah misalnya, nilai dZ/dp, kemiringan grafik faktor penempatan terhadap tekanan. Untuk gas sempurna berlaku dZ/dp = 0, tetapi untuk gas nyata berlaku dZ = B’ + 2Pc’ + . . . dp B’ ketika p 0 Namun demikian, B’ tidak perlu nol. Oleh karena itu, walaupun untuk gas nyata Z 1 ketika p 0 (dan lebih umum, persamaan keadaan gas nyata sama dengan hukum gas sempurna ketika p 0), kemiringan kurva Z terhadap p tidak mendekati nol (nilai gas sempurna. Karena sifat-sifat lain yang akan (yang akan kita lihat nanti) juga begantung pada turunan-turunan, sifat-sifat gas nyata tidak selalu sama dengan nilai-nilai gas sempurna pada tekanan rendah. 2.2 Sifat-sifat Gas Nyata Sifat gas nyata: Volume molekul gas nyata tidak dapat diabaikan Terdapat gaya tarik menarik antara molekul-molekul gas terutama jika tekanan diperbesar atau volum diperkecil Adanya interaksi atau gaya tarik menarik antar molekul gas nyata yang sangat kuat, menyebabkan gerakan molekulnya tidak lurus, dan tekanan ke dinding menjadi kecil, lebih kecil daripada gas ideal. Memenuhi persamaan (P + a ) (V – b ) = R T (a.4 a) V2 Atau P= RT (V – b) a (a.4 b) 2 V Dimana : P = Tekanan absolut gas (atm) V = Volume spesifik gas (liter) R = Konstanta gas (0,082 L.atm/mol atau 8,314J/Kmol) T = Suhu /temperatur absolut gas (K) n = Jumlah mol gas a,b = Konstanta Van der Waals 7 2.3 Persamaan Van Der Walls Persamaan Van der Walls, merupakan salah satu bentuk persamaan yang lebih mendekati realitas. Meskipun demikian, persamaan inipun belum sepenuhnya benar. Untuk mendapatkan persamaan ini, kita berangkat dari persamaan serta sifat gas ideal. Masalah yang akan dibahas, berangkat dari fakta, bahwa pengukuran terhadap gas real, menyimpang dari keidealan. Diduga, bahwa penyimpangan gas real terhadap keidealan disebabkan karena terdapat dua syarat keidealan yang tidak pernah dapat dipenuhi oleh gas real, yaitu : 1. Molekul – molekul gas ideal dipandang sebagai titik massa yang tak bervolume atau tidak memakan tempat. Dengan demikian jika ke dalam ruangan dimasukkan gas, maka seolah- olah partikel gas tidak membutuhkan tempat. Padahal sebenarnya, tidak ada materi yang tidak makan tempat. Itulah sebabnya maka volume gas real lebih besar dari pada gas ideal. Jika penyimpangan volume ini disebut b, maka hubungan antara V gas real dan V gas ideal adalah : V = Vid + b (a.1) Atau Vid = V – b dengan V adalah volume molar gas real sedangkan Vid adalah volume molar gas ideal. 2. Pada gas ideal diasumsikan bahwa setiap partikal molekul bekerja gaya atraksi sedemikian rupa sehingga resultantenya = 0, atau dengan perkataan lain, pada molekul gas ideal tidak terdapat gaya atraksi sama sekali. Padahal kenyataannya, untuk molekul – molekul yang berada didekat dinding, masih bekerja gaya straksi. Pengabaian gaya atraksi yang besarnya berbanding terbalik kuadrat volume atau a/V2 inilah yang mengakibatkan pengecilan tekanan gas real dibandingkan gas ideal dalam relasi : Pid = p + a V2 dengan p adalah tekanan gas real. (a.2) Untuk mendapatkan persamaan Van der Walls, kita bertolak dari persamaan gas ideal. Karena sesungguhnya persamaan Van der Walls adalah persamaan gas ideal 8 yang dimodifikasi dengan memperhitungkan volume partikel serta atraksi antar molekul. Telah kita ketahui bahwa untuk gas ideal berlaku : pid Vid = R T Jika persamaan 1, dimasukkan ke dalam persamaan ini di atas, maka di peroleh : pid ( V b ) R T (a.3) Selanjutnya, substitusi persamaan (2) ke dalam persamaan (3), menghasilkan : (P + a ) (V – b ) = R T (a.4 a) 2 V Atau P= RT (V – b) a V2 (a.4 b) Persamaan (4 a) atau (4 b) itulah yang disebut persamaan Van der Walls. Tabel 1.1 Koefisien van der walls pada temperatur 298 K. a/ b/ 2 -2 -2 (atm L mol ) (10 L mol-2) Ar 1,325 3,22 CO2 3,592 4,267 He 0,034 2,37 N2 1,390 3,913 Penyusunan persamaan Interaksi tolak-menolak antara molekul –molekul diperhitungkan dengan asumsi bahwa interaksi itu menyebabkan molekul-molekul beroerilaku seperti bola kecil tetapi tidak dapat ditembus. Volume bukan nol molekul menyiratkan bahwa partikel itu tidak bergerak didalam volume V, melainkan terkekeng didalam volume yang lebih kecil V – nb, dengan menyatakan perkiraan volume total yang ditempati molekul-molekul sendiri. Dengan alasan ini kita terdorong untuk mengubah hukum gas sempurna p=nRT/V menjadi : p = nRT V – nb Tekanan bergantung baik pada frekuensi tabrakan dengan dinding maupun dengan gaya setiap tabrakan. Baik frekuensi maupun gaya tabrakan berkurang akibat gaya tarik. Yang terjadi akibat kekuatan yang secara kasar sabanding dengan konsentrasi molar n/V molekul-molekul di dalam sampel. Oleh karena itu, tekanan berkurang sebanding dengan 9 kuadrat konsentrasi ini. Jika pengurangan tekanan ditulis sebagai –a(n/V)2, dengan a menyatakan konstanta yang khas untuk setiap gas, maka efek gabungan dari gaya tolak dan gaya tarik adalah persamaan Van Der Walls : p = nRT a n 2 (1 a) V – nb V Persamaan ini sering ditulis dalam istilah volume molar Vm 2 = V/m sebagai : p = nRT Vm – nb a Vm2 (1 b) Istilah a/Vm disebut tekanan internal gas. Terkadang lebih baik untuk menata ulang persamaan tersebut menjadi bentuk yang menyerupai pV = nRT : p + an2 (V – nb) = nRT V2 (1 c) (P.W.ATKINS : 1996 : 19) Ciri-ciri utama persamaan Van Der Walls : a) Isoterm gas sempurna diperoleh pada temperatur tinggi dan volume molar besar. Jika temperatur tinggi, RT dapat menjadi begtu besar sehingga suku pertama dan dalam persamaan 1b jauh lebih melebihi suku keduanya. Lagi pula, jika volume molar besar (dalam arti Vm >> b), kita dapat menggantikan penyebutnya Vm – dengan Vm. Dengan demikian, persamaan menjadi lebih sederhana p=RT/Vm , persamaan gas sempurna. b) Cairan dan gas berada bersama-sama jika efek kohesi dan dispersiberada dalamkeseimbangan. Lengkungan can der walls terjadi jika kedua suku dalam persamaan 1b sama besar. Suku pertama berasal dari energi kinetik molekul dan interaksi tolak menolaknya; suku kedua menggambarkan efek interaksi tarik menarik. c) Konstanta kritis berhubungan dengan koefisien-koefisien van der walls. Untuk T > Tc isoterm hasil hitungan berosilasi dan masing-masing mencapai nilai minimum, kemudian diikuti dengan nilai maksimu. Nilai–nilai ekstrem ini saling mendekat sewaktu T Tc dan akan sama nilainya pada T = Tc, dan pada titik kritis, kurva mempunyai perubahan datar. Dari sifat-sifat kurva, kita tahu bahwa perubahan semacam ini terjadi jika baik turunan pertama maupun kedua bernilai nol. Dengan demikian, kita dapat menemukan konstanta kritis dengan menghitung turunan-turunan tersebut dan membuatnya sama dengan nol. 10 2.4 Faktor Kompresibilitas (Z) Gas Van Der Walls Telah diuraikan bahwa pengukuran terhadap tekanan, volume molar serta temperatur suatu gas tidak memenuhi persaman p V = RT, dan itu terjadi pada sembarang gas. Karena menyimpang dari sifat keidealan maka gas real juga disebut gas non ideal. Pernyataan kuantitatif atas besarnya penyimpangan terhadap keidealan, disebut faktor kompresibilitas Z (berbeda dengan koefisien kompresibilitas K) dengan Z adalah resiko antar volume molar suatu gas yang diamati atau gas real (V), dengan volume molar gas ideal (V id). Jadi : Z=V Vid (b.1) Karena Vid = RT/p maka : Z=pV atau Z=p V RT (b.2) RT Untuk gas ideal, harga Z = 1, dan tidak bergantung pada temperatur dan tekanan, sedangkan untuk gas real Z merupakan fungsi temperatur dan tekanan atau ditulis Z = f (T.p). Untuk mendapatkan harga Z dan hubungannya dengan T dan p, kita ikuti langkah – langkah berikut : Jika harga p pada persamaan (a.4 b) dimasukka ke dalam persamaan (b.2), akan diperoleh : Z= R T (V – b) a V V 2 RT Atau (b.3) Z= V ( V – b) a VRT Suku pertama ruas kanan persamaan (b.3) di atas dibagi dengan V baik pembilang maupun penyebutannya, sehingga persamaan (b.3) menjadi : Z= 1 a V R TV b 1-V Tujuan mengubah suku pertama menjadi berbentuk (b.4) 1 , karena dalam matematika, b 1-V mengenai deret terdapat hubungan bahwa : 1 = 1 + x + x2 + x3 + x4 ................... 1–x (b.5) Asal x mendekati nol. Padahal b/V jelas mendekati nol, sehingga dengan menggunakan sifat persamaan (b.4 ) dapat ditulis : 11 1 = 1 + b/V + (b/V)2 + (b/V)3........... (b.6) b 1- V Jika persamaan (b.6) dimasukkan ke dalam persamaan (b.4), dihasilkan : Z = 1 + b/V + (b/V)2 + (b/V)3.......... a VRT Atau Z = 1 + b/V a + (b/V)2 + (b/V)3........ VRT Z=1(b – a ) / V+ (b/V)2 + (b/V)3............. R T Atau (b.7) Persamaan (b.7) adalah Z sebagai fungsi volume, sedang lazimnya Z dinyatakan sebagai fungsi volume. Untuk itu V harus dinyatakan dalam p. Sudah barang tentu, seharusnya relasi yang digunakan harus relasi Van der Walls, tetapi mencari harga V dalam p untuk relasi Van der Walls, tentu tidak sederhana, karena persamaan Van der Walls merupakan persamaan order 3 dalam V. oleh karena itu kita menggunakan relasi gas ideal untuk mengubah V dalam p, yaitu : V=p/RT Sehingga persamaan (b.7) menjadi : Z = 1 + 1 ( b - a ) p + ( b )2 P2 + ( b )3 P3 + ........ R T R T R T R T (b.8) Persamaan (b.8) itulah Z sebagai fungsi T dan p yang dicari. 2.5 Koefisien Virial 12 Untuk gas karbondioksida o Pada temperatur tinggi (>50°C) dan volume molar tinggi (Vm > 0.3 L/mol), garis isotherm terlihat mendekati gas ideal o Kammerlingh-Onnes (1911) telah mengkaji pola gas nyata dengan pendekatan menggunakan ekspansi virial (persamaan deret) CO2 pVm = RT (1 + B’p + C’p . . .) Lebih umum dengan berbasis n/V (1/Vm) yang lebih pVm = RT 1+B+C+... Vm Vm o B, C… tergantung pada temperatur o B, C… disebut koefisien virial kedua, ketiga…. Persamaan Virial pVm = RT (1 + B’p + C’p . . .) o Koefisien harus ditentukan berdasarkan eksperimen o Nilai koefisien ketiga dan seterusnya sangat kecil dibandingkan koefisien kedua : B/Vm >> C/Vm2 o Gambaran koefisien virial kedua untuk berbagai gas pada variasi temperatur 13 Persamaan Virial pVm = RT (1 + B’p + C’p . . .) Untuk campuran, koefisien tergantung pada fraksi mol B = x12B11 + 2 x1 x2 B12 + x22B22 x1x2 B12 menunjukan interaksi diantara kedua gas pVm = RT (1 + B’p + C’p . . .) Faktor kompresi, Z, adalah fungsi dari p dan T 14 Untuk gas ideal dZ/dp (slope grafik) = 0 Untuk gas nyata, dZ/dp dapat ditentukan dengan persamaan virial : Substitusikan Vm (V = Z V °); dan V °=RT/p Slope = dZ/dP = B’ + 2pC’+ …. Pada saat p → 0, dZ/dP → B’, Namun demikian nilai B’ sendiri tidak perlu 0. karena itu meskipun gas nyata Z → 1 ketika p 0, maka kemiringan kurva Z terhadap p tidak mendekati nol (nilai gas sempurna) Persamaan Koefisien Virial Pada volume besar dan temperatur tinggi, isoterm gas nyata dan isoterm gas sempurna tidak jauh berbeda. Perbedaan kecil ini menunjukkan bahwa hukum gas sempurna berlaku pada tekanan rendah dan pada kenyataannya merupakan suku pertama dalam pernyataan yang berbentuk. pVm = RT (1 + B’p + C’p . . .) Dalam banyak penerapan, deret yang lebih cocok adalah pVm = RT 1+B+C+... Vm Vm Pernyataan tersebut adalah dua versi dari persamaan keadaan virial (nama ini berasal dari kata latin untuk gaya). B, C, . . . , yang bergantung pada temperatur, adalah koefisien virial yng kedua, ketiga, . . . , koefisien virial yng ketiga C biasanya kurang penting ketimbang yang kedua B dalam arti bahwa volume molar khas C/V m2 << B/Vm. Persamaan virial adalah contoh pertama dri prosedur umum dalam kimia fisika, dimana satu hukum sederhana (dalam hal ini pV = nRT) dianggap sebagai suku pertama deret pangkat satu variabel (dalam hal ini p atau Vm ). Persamaan virial dapat digunakan untuk memeragakan suatu hal penting yaitu walaupun persamaan keadaan gas nyata dapat sama dengan gas sempurna sewaktu p 0, semua sifat-sifatnya tidak perlu sama dengan sifat-sifat gas sempurna. Perhatikanlah misalnya, nilai dZ/dp, kemiringan grafik faktor penempatan terhadap tekanan. Untuk gas sempurna berlaku dZ/dp = 0, tetapi untuk gas nyata berlaku dZ = B’ + 2Pc’ + . . . dp B’ ketika p 0 Namun demikian, B’ tidak perlu nol. Oleh karena itu, walaupun untuk gas nyata Z 1 ketika p 0 (dan lebih umum, persamaan keadaan gas nyata sama dengan hukum 15 gas sempurna ketika p 0), kemiringan kurva Z terhadap p tidak mendekati nol (nilai gas sempurna. Karena sifat-sifat lain yang akan (yang akan kita lihat nanti) juga begantung pada turunan-turunan, sifat-sifat gas nyata tidak selalu sama dengan nilai-nilai gas sempurna pada tekanan rendah. 2.6 Pengembunan Sekarang, bayangkanlah apa yang terjadi jika volume suatu sampel gas yang mula-mula berada pada keadaan tertanda A dalam gambar diatas dikurangi pada temperatur tetap (dengan cara memanpatkannya di dalam sebuah piston). Didekat A, tekanan gas naik kurang lebih sesuai dengan hukum Boyle. Penyimpangan serius dari hukum itu mulai tampak ketika volume sudah berkurang sampai B. Pada C (yang sama dengan kira-kira 60 atm dalam hal karbondioksida), semua kemiringan dengan perilaku sempurna hilang, karena mendadak piston bergerser masuk tanpa ada kenaikan tekanan : ditandai dengan garis mendatar CDE. Pemeriksaan isi silinder memperlihatkan bahwa tepat disebelah kiri C muncul cairan, dan terdapat dua fase yang dipisahkanoleh permukaan yang jelas. Sewaktu volume terus dikecilkan dari C melalui D ke E, jumlah cairan bertambah. Pada tahap ini tidak ada tambahan tahanan pada piston karena gas dapat menggapinya dengan mengembun. Tekanan yang berpadanan dengan garis CDE, pada saat baik cairan maupun uap ada dalam kesetimbangan, disebut tekanan uap cairan ini pada temperatur eksperimen. 16 Pada E, semua sampel berwujud cairan dan piston berhenti pada permukaan cairan. Pengurangan volume lebih jauh memerlukan pengerahan tekanan yang besae. Hal itu diperlihatkan dengan garis yang menanjak tajam disebelah kiri E. Bahkan sedikit pengurangan volume dari E ke F memerlukan penambahan tekanan yang besar. Pengembunan Pada suatu temperatur T konstan, jika suatu gas nyataditekan dengan mengikuti isoterm berawal dari A, terlihat : o Di dekat A, p meningkat mengikuti hukum Boyle(kelakuan sebagai gas nyata) o Mulai dari B sampai ke C mulai terjadi penyimpangan hukum Boyle, tetapi p tetap o bertambah o Pada titik C, p berhenti tidak bertambah (untuk CO2,~ 60 atm) o Sifat gas ideal hilang o Cairan mulai muncul dan terdapat dua fasa sepanjang garis CE o Gas tetap ada pada setiap titik karena kompresi diimbangi dengan pengembunan. Tekanan pada kondisi garis CDE ini yakni saat cairan dan uap berada pada keadaankesetimbangan disebut tekanan uap dari cairanpada temperatur eksperimen. o Pada titik E, seluruh gas mengembun menjadi cairan o Pengurangan volume lebih jauh akan memerlukan pengerahan tekanan yang sangat besar. 2.7 Konstanta Kritis Konstanta Kritis 17 Untuk kasus CO2 pada isoterm T 404,19K atau 31,04 oC, terdapat keadaan istimewa pada teori keadaan materi, yang disebut temperatur kritis (Tc). Pada kondisi ini dua fasa cair dan gas tidak berlangsung dan berimpit pada satu titik tunggal, tanda * di kurva, yang disebut sebagai titik kritis. Kondisi pada titik kritis ini dinamakan konstanta kritis meliputi : a) Temperatur kritis (Tc) b) Tekanan kritis (Pc) Volume molar kritis (Vc) Di atas Tc hanya ada fase gas, jadi fasecairan suatu zat tidak mungkin terbentuk. Konstanta Kritis Untuk Variasi Gas 2.8 Asas Keadaan Yang Bersesuaian Sebagai skala relatif untuk membandingkan sifat beberapa obyek Menggunakan konstanta kritis sebagai sifat fisik suatu gas maka akan diperoleh skala baru. a) Tekanan Tereduksi : pr = p pc b) Volume Tereduksi : Vr = Vm Vc c) Temperatur Tereduksi : Tr = T Tc 18 Pengamatan yang mewujudkan gas nyata pada volume dan temperatur yang sama melakukan tekanan tereduksi yang sama disebut asas keadaan yang bersesuaian. Persamaan keadaan lain o Persamaan virial adalah bersifat fenomenologikal dimana konstantanya tertentu untuk suatu gas dan harus ditentukan secara eksperimen. o Beberapa persamaan keadaan untuk gas nyata antara lain adalah: a) Berthelot (1898) Lebih baik dari pada persamaan Van Der Walls pada tekanan yang tidak lebih dari 1 atm P + n2a (V – nB) = nRT TV2 A, B merupakan suatu konstanta b) Dieterichi (1899) p = Rte –a/RTVm Vm c) Beattie-Bridgeman p = (1 -RT (Vm + Vm2 a0 1 + a Vm b0 1 + b Vm C0 VmT3 d) Virial (Kammrlingh Onnes) pVm = RT 1+B+C+... Vm Vm 2.9 Fugasitas Gas Nyata Fugasitas Potensial kimia gas ideal adalah fungsi dari tekanan gas, sedangkan untuk gas nyata, diberikan dengan hubungan : 19 R T ln f (c.1) Lim (c.2) p 0 f =1 p yaitu apabila tekanan mendekati nol, fugasitas mendekati tekanan. Dengan kata lain untuk gas ideal, tekanan dan fugasitas adalah sama, dan secara fisika fugasitas adalah ukuran dari tekanan gas nyata. adalah potensial kimia standar, yaitu potensial kimia bila fugasitas adalah satu. Ketergantungan Fugasitas pada Tekanan Perubahan fugasitas dengan berubahnya tekanan diberikan oleh : Ln f2 – f1 = p2 V d p p1 (c.3) Dengan mengetahui harga fugasitas pada satu tekanan, harga pada tekanan lain dapat diperoleh baik dengan mengevaluasi integral secara grafik atau secara analitis. Ketergantungan Fugasitas pada Temperatur Perubahan fugasitas dengan berubahnya temperatur diberikan oleh : 𝜕 ln f 𝜕𝑇 = H* - H RT2 2 Dimana H* adalah entalpi molar parsial dari zat dalam keadaan A* yaitu pada tekanan nol. Maka perbedaan (H* - H) adalah perubahan entalpi molar bila zat dibawa dari keadaan A menuju keadaan dengan tekanan nol. Kadang-kadang disebut juga “panas penguapan molar idea” untuk keadaan yang diketahui. Jika keadaan yang diketahui adalah gasa juga, maka disebut Panas Joule Thompson. Perhitungan Fugasitas dari Gas Nyata Fugasitas gas nyata dapat dievaluasi baik secara grafik maupun secara analitis : 1. Dengan Metode Grafik i. Menggunakan fungsi : Fugasitsa setiap gas nyata pada tekanan p diberikan sebagai : Ln f = ln p + 1 R T P dp (c.4 a) 0 20 Dimana = ( - R T + V ), p adalah tekanan gas nyata, V adalah volume 1 mol gas P gas nyata dan adalah perbedaan volume molar gas ideal dan gas nyata. Integral dapat dievaluasi secara grafik, yaitu daerah dibawah kurva yang merupakan plot terhadap p. ii. Berdasarkan Faktor Kompresibilitas : persamaan (c.4) dapat ditulis sebagai : Ln f = ln p - p 0 1 – Z dp p (c.4 b) Integral dapat dievaluasi secara grafik dengan memplot (1 – Z) / p terhadap p dan dengan mengukur daerah bawah kurva. Untuk gas-gas di bawah temperatur, (1 – Z) adalah positif pada temperatur sedang, sehingga fugasitas akan lebih kecil dari tekanan. Untuk gas-gas diatas temperatu, fugasitas akanlebih besar dari tekanan. 2. Metode Analitis Perilaku gas nyata dapat dinyatakan oleh persamaan keadaan yang berbeda. Dengan menggunakan persamaan keadaan utama, integral diatas dapat dievaluasi, sehingga fugasitas dapat dihitung. 21 BAB III PENUTUP 3.1 Kesimpulan Gas yang mengikuti hukum Boyle dan hukum Charles, yakni hukum gas ideal, disebut gas ideal. Namun, didapatkan, bahwa gas yang kita jumpai, yakni gas nyata, tidak secara ketat mengikuti hukum gas ideal. Semakin rendah tekanan gas pada temperatur tetap, semakin kecil deviasinya dari perilaku ideal. Semakin tinggi tekanan gas, atau dengan dengan kata lain, semakin kecil jarak intermolekulnya, semakin besar deviasinya. Gas nyata memiliki sifat : Volume molekul gas nyata tidak dapat diabaikan Terdapat gaya tarik menarik antara molekul-molekul gas terutama jika tekanan diperbesar atau volum diperkecil Adanya interaksi atau gaya tarik menarik antar molekul gas nyata yang sangat kuat, menyebabkan gerakan molekulnya tidak lurus, dan tekanan ke dinding menjadi kecil, lebih kecil daripada gas ideal. Memenuhi persamaan (P + a ) (V – b ) = R T (a.4 a) 2 V Atau P= RT (V – b) a (a.4 b) V2 Dimana : P = Tekanan absolut gas (atm) V = Volume spesifik gas (liter) R = Konstanta gas (0,082 L.atm/mol atau 8,314J/Kmol) T = Suhu /temperatur absolut gas (K) n = Jumlah mol gas a,b = Konstanta Van der Waals Fisikawan Belanda Johannes Diderik van der Waals (1837-1923) mengusulkan persamaan keadaan gas nyata, yang dinyatakan sebagai persamaan keadaan van der Waals ataupersamaan van der Waals. Ia memodifikasi persamaan gas ideal (persamaaan 6.5) dengan cara sebagai berikut: dengan menambahkan koreksi pada P untuk 22 mengkompensasi interaksi antarmolekul; mengurangi dari suku V yang menjelaskan volume real molekul gas. Sehingga didapat: (P + a ) (V – b ) = R T V2 Atau P= RT (V – b) (a.4 a) a (a.4 b) V2 Pernyataan kuantitatif atas besarnya penyimpangan terhadap keidealan, disebut faktor kompresibilitas Z (berbeda dengan koefisien kompresibilitas K) dengan Z adalah resiko antar volume molar suatu gas yang diamati atau gas real (V), dengan volume molar gas ideal (V id). Jadi : Z=V Vid (b.1) Karena Vid = RT/p maka : Z=pV atau Z=p V RT (b.2) RT Persamaan virial adalah bersifat fenomenologikal dimana konstantanya tertentu untuk suatu gas dan harus ditentukan secara eksperimen. Pada volume besar dan temperatur tinggi, isoterm gas nyata dan isoterm gas sempurna tidak jauh berbeda. Perbedaan kecil ini menunjukkan bahwa hukum gas sempurna berlaku pada tekanan rendah dan pada kenyataannya merupakan suku pertama dalam pernyataan yang berbentuk. pVm = RT (1 + B’p + C’p . . .) Dalam banyak penerapan, deret yang lebih cocok adalah pVm = RT 1+B+C+... Vm Vm Asas Keadaan yang bersesuaian merupakan Sebagai skala relatif untuk membandingkan sifat beberapa obyek Tekanan Tereduksi : pr = p pc Volume Tereduksi : Vr = Vm Vc 23 Temperatur Tereduksi : Tr = T Tc Fugasitas gas nyata dapat dievaluasi baik secara grafik maupun secara analitis: Dengan Metode Grafik iii. Menggunakan fungsi : Fugasitsa setiap gas nyata pada tekanan p diberikan sebagai : Ln f = ln p + 1 R T P dp (c.4 a) 0 Dimana = ( - R T + V ), p adalah tekanan gas nyata, V adalah volume 1 mol gas P gas nyata dan adalah perbedaan volume molar gas ideal dan gas nyata. Integral dapat dievaluasi secara grafik, yaitu daerah dibawah kurva yang merupakan plot terhadap p. iv. Berdasarkan Faktor Kompresibilitas : persamaan (c.4) dapat ditulis sebagai : Ln f = ln p - p 0 1 – Z dp p (c.4 b) 24