Metode Bagi 2

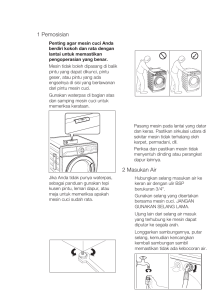
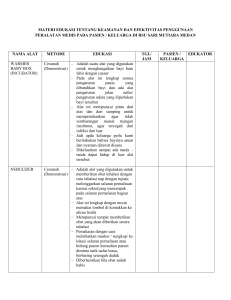
Akar dari suatu persamaan biasa juga disebut penyelesaian dari suatu persamaan.
Tidak semua persamaan dapat diselesaikan secara analitik. Untuk menyelesaikan persamaan
yang demikian dapat digunakan metode numerik. Beberapa metode yang dapat digunakan
adalah:
1. Metode Bagi Dua
2. Metode Posisi Palsu
3. Metode Newton-Raphson
4. Metode Secant
2. Metode Bagi Dua
Metode Bagi Dua merupakan metode yang paling sederhana. Sebelum menggunakan
metode ini diperlukan satu selang akar. Idenya selang akar tersebut kita bagi dua sama besar,
kemudian pilih satu bagian yang mengandung akar sebagai selang baru. Hal ini dilakukan
secara berulang sampai lebar selang kurang dari toleransi yang diinginkan.
Secara geometris proses tersebut dapat dilihat pada Gambar 2.5. Selang akar [a, b]
dibagi dua di T1. Terbentuk dua selang yaitu [a, T1] dan [T1, b]. Dari dua selang ini yang
memuat akar adalah [a, T1], sehingga [a, T 1] menjadi selang baru. Selanjutnya jika selang baru
lebarnya kurang dari toleransi yang diberikan maka akar dari persamaan adalah T 1. Jika belum
memenuhi, bagi dua lagi selang [a, T 1], sehingga diperoleh T2, dan terbentuk selang baru lagi
[T2, T1]. Proses diteruskan sampai diperoleh selang baru yang lebarnya kurang dari toleransi.
b
a
T1
a
T2
T1
[a,b]
[a,T1]
[T2,T1]
Gambar 2.5 Metode Bagi Dua
Jika diketahui (a, fa) dan (b, fb), maka untu menentukan T dapat dihitung dengan rumus
𝑇=
𝑏−𝑎
2
(2.2.1)
Berdasarkan uraian di atas maka algoritma untuk metode bagi dua adalah sebagai
berikut:
Algoritma
1. Tetapkan selang akar [a, b] sedemikian hingga f(a) . f(b) < 0
2. Hitung Titik baru: T 
ba
2
3. Hitung f(T)
4. Jika f(a).f(T) < 0, maka b = T, selang baru [a, T]
Jika f(a).f(T) > 0, maka a = T, selang baru [T, b]
Jika f(a).f(T) = 0, maka akar = T, selesai
5. Jika |a - b|=|selang baru|≤ toleransi, maka akar adalah T, selesai
6. Kembali ke 1
Contoh 2.3:
Tentukan akar positif terbesar dari persamaan
𝑓 (𝑥 ) = 3sin(𝑥) − 𝑥 + 1 = 0
Hitung dengan toleransi 0,001.
Penyelesaian:
Berdasarkan contoh 2.1, dapat diketahui bahwa akar terbesar dari persamaan tersebut berada
pada selang (2, 3).
Iterasi 1:
1. Selang akar (2, 3)
a = 2;
f (a) = 1,72789
b = 3;
f (b) = -1,57664
2. 𝑇 =
2+3
2
= 2,5
3. 𝑓 (𝑇) = 3 sin(2,5) − 2,5 + 1 = 0,29542
4. 𝑓 (𝑎). 𝑓(𝑇) > 0, maka a = 2,5, selang baru (2,5, 3)
5. |2,5 − 3| = 0,5 > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 2
Iterasi 2:
1. Selang akar (2,5, 3)
a = 2,5 ;
f (a) = 0,2954164
b = 3;
f (b) = -1,57664
2. 𝑇 =
2,5+3
2
= 2,75
3. 𝑓 (𝑇) = 3 sin(2,75) − 2,75 + 1 = −0,605017
4. 𝑓 (𝑎). 𝑓(𝑇) < 0, maka b = 2,75, selang baru (2,5, 2,75)
5. |2,5 − 2,75| = 0,25 > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 3
Iterasi 3:
1. Selang akar (2,5, 2,75)
a = 2,5 ;
f (a) = 0,2954164
b = 2,75;
f (b) = −0,605017
2. 𝑇 =
2,5+2,75
2
= 2,625
3. 𝑓 (𝑇) = 3 sin(2,625) − 2,625 + 1 = −0,1432491
4. 𝑓 (𝑎). 𝑓(𝑇) < 0, maka b = 2,625, selang baru (2,5, 2,625)
5. |2,5 − 2,625| = 0,125 > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 4
Dan seterusnya. Langkah penyelesaian di atas dapat diringkas dalam bentuk table sebagai
berikut:
iterasi
a
B
f (a)
f (b)
3
1.727892
-1.57664
1
2
2
2.5
3
0.295416
3
2.5
2.75
0.295416
4
2.5
2.625
5
2.5625
6
T
f (T)
|selang Baru|
2.5
0.295416
0.5
-1.57664
2.75
-0.60502
0.25
-0.60502
2.625
-0.14324
0.125
0.295416
-0.14324
2.5625
0.079294
0.0625
2.625
0.079294
-0.14324
2.59375
-0.03121
0.03125
2.5625
2.59375
0.079294
-0.03121
2.578125
0.024238
0.015625
7
2.578125
2.59375
0.024238
-0.03121
2.585938
-0.00344
0.0078125
8
2.578125
2.585938
0.024238
-0.00344
2.582031
0.010412
0.00390625
9
2.582031
2.585938
0.010412
-0.00344
2.583984
0.00349
0.001953125
10
2.583984
2.585938
0.00349
-0.00344
2.584961
2.72E-05
0.000976563
11
2.584961
2.585938
Berdasarkan Tabel di atas, pada iterasi ke-10 diperoleh
|selang Baru| = 0.000976563 < toleransi.
Sehingga proses berhenti pada itersi ke-10, dan akar dari positif terbesar dari persamaan
𝑓 (𝑥 ) = 3sin(𝑥) − 𝑥 + 1 = 0 adalah 2,584961.
Latihan 2
1. Tentukan salah satu akar positif dari persamaan 𝑓 (𝑥 ) = 𝑥 6 − 𝑥 − 1 = 0 dengan
toleransi tidak lebih dari 0,05!
Iterasi 1:
1. Selang akar (….,....)
a = ….;
f (a) = ….
b = ….;
f (b) = …
2. 𝑇 =
…..+...
…..
=⋯
3. 𝑓 (𝑇) = ⋯
4. 𝑓 (𝑎). 𝑓(𝑇) … . . 0, maka …..=....., selang baru (....,.....)
5. |… −. . . | = ⋯ > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 2
Iterasi 2:
1. Selang akar (....,....)
a = ....;
f (a) = ....
b = ....;
2. 𝑇 =
….+...
…
f (b) = ....
=⋯
3. 𝑓 (𝑇) = ⋯
4. 𝑓 (𝑎). 𝑓(𝑇) … . . 0, maka …. = ...., selang baru (....,.....)
5. |… −. . . | = ⋯ > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 3
Iterasi 3:
1. Selang akar (....,....)
a = ....;
f (a) = ....
b = ....;
2. 𝑇 =
….+...
…
f (b) = ....
=⋯
3. 𝑓 (𝑇) = ⋯
4. 𝑓 (𝑎). 𝑓 (𝑇) … . . 0, maka …. = ...., selang baru (....,.....)
5. |… −. . . | = ⋯ > 𝑇𝑜𝑙𝑒𝑟𝑎𝑠𝑖, lanjut iterasi 3
Iterasi 4:
Iterasi 5:
Berdasarkan proses perhitungan di atas, pada iterasi ke-.... diperoleh
|selang Baru| = ..... < toleransi.
Sehingga proses berhenti pada itersi ke-...., dan akar dari positif terbesar dari persamaan
𝑓(𝑥 ) = 𝑥 6 − 𝑥 − 1 = 0 adalah ....................... .
2. Carilah akar dari 𝑓 (𝑥 ) = 𝑥 3 − 𝑥 − 1 = 0 di dalam 1,2 dengan Metode Bagi Dua
dengan toleransi 0,01!
Iterasi
1
2
3
a
b
f (a)
f (b)
T
f (T)
|selang Baru|
1
2
-1
5
1,5
0,875
0.5
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
....
4
5
6
7
8
9
3. Carilah akar dari 𝑓 (𝑥 ) = 𝑥 sin 𝑥 − 0,1 = 0 dengan menggunakan Metode Bagi Dua
dengan tolerasi 0,001!