soal

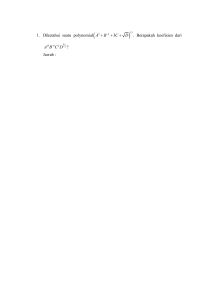
Diberikan d = (7n + 5, 5n + 4), dengan n adalah bilangan bulat positif..
Buktikan bahwa untuk setiap bilangan bulat positif n berlaku d = 1 atau d = 3.
(Hint. Jika a | b, maka a | cb, untuk bilangan bulat positif c).
Bukti :
Dari diketahui jika a|b maka a|cb sehingga terdapat ( a,b ) = 1
Oleh karena itu misalkan d|7n+5 dan d|5n+4 dari sifat keterbagian maka diperoleh
d|(7n+5)+(5n+4)  d|(12n+9)  d|3(4n+3)
d|(7n+5)-(5n+4)  d|(2n-1)  d|1(2n-1)
akibatnya haruslah d = 3 atau d = 1