INVERSI

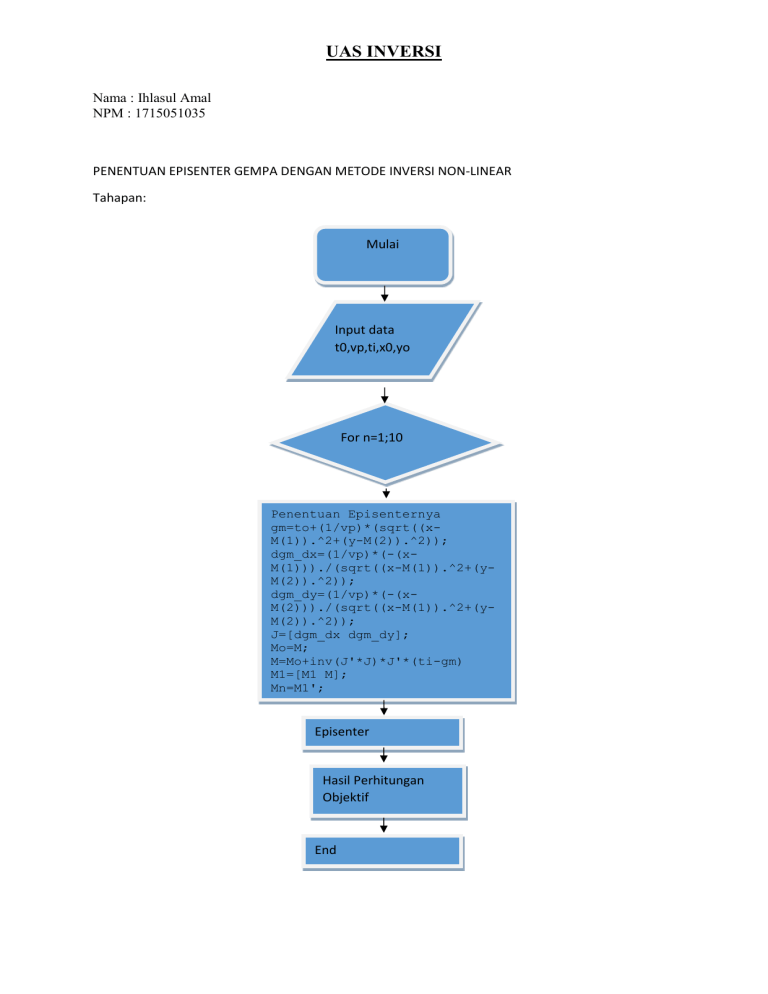
UAS INVERSI
Nama : Ihlasul Amal
NPM : 1715051035
PENENTUAN EPISENTER GEMPA DENGAN METODE INVERSI NON-LINEAR
Tahapan:
Mulai
Input data
t0,vp,ti,x0,yo
For n=1;10
Penentuan Episenternya
gm=to+(1/vp)*(sqrt((xM(1)).^2+(y-M(2)).^2));
dgm_dx=(1/vp)*(-(xM(1)))./(sqrt((x-M(1)).^2+(yM(2)).^2));
dgm_dy=(1/vp)*(-(xM(2)))./(sqrt((x-M(1)).^2+(yM(2)).^2));
J=[dgm_dx dgm_dy];
Mo=M;
M=Mo+inv(J'*J)*J'*(ti-gm)
M1=[M1 M];
Mn=M1';
Episenter
Hasil Perhitungan
Objektif
End
Data yang digunakan :
STASIUN
ST1
ST2
ST3
ST4
Bujur (km)
20
50
40
10
Lintang
(km)
Waktu tempuh Gelombang pada masing-masing stasiun
10
25
50
40
Script yang digunakan :
clear all
clc
to=0; % origin time
vp=4; % kecepatan gelombang gempa
ti=[7.1;1.8;5;7.9]; % waktu tempuh masing2 stasiun
x=[20;50;40;10];
y=[10;25;50;40]; % posisi stasiun
h=length(x);
figure(1)
stem(x,y,'h')
hold on
grid on
figure(2)
M=[40;30]; % posisi tebakan awal
[X,Y]=meshgrid(0:10:80,0:10:80);
plot(X,Y,'o-')
grid on
figure(3)
M1=[];
for n=1:5
gm=to+(1/vp)*(sqrt((x-M(1)).^2+(y-M(2)).^2));
dgm_dx=(1/vp)*(-(x-M(1)))./(sqrt((x-M(1)).^2+(y-M(2)).^2));
dgm_dy=(1/vp)*(-(x-M(2)))./(sqrt((x-M(1)).^2+(y-M(2)).^2));
J=[dgm_dx dgm_dy];
Mo=M;
M=Mo+inv(J'*J)*J'*(ti-gm)
M1=[M1 M];
Mn=M1';
end;
plot(Mn(:,1),Mn(:,2),'o')
hold on
plot(Mn(:,1),Mn(:,2))
% oleh stasiun pertama
t_cal1=to+(1/vp)*sqrt((x(1)-X).^2+(y(1)-Y).^2);
Error1=(t_cal1-ti(1)).^2;
% oleh stasiun kedua
t_cal2=to+(1/vp)*sqrt((x(2)-X).^2+(y(2)-Y).^2);
Error2=(t_cal2-ti(2)).^2;
% oleh stasiun ketiga
7,1
1,8
5
7,9
t_cal3=to+(1/vp)*sqrt((x(3)-X).^2+(y(3)-Y).^2);
Error3=(t_cal3-ti(3)).^2;
% oleh stasiun keempat
t_cal4=to+(1/vp)*sqrt((x(4)-X).^2+(y(4)-Y).^2);
Error4=(t_cal4-ti(4)).^2;
Erms=sqrt((1/n)*(Error1+Error2+Error3+Error4));
[cs,h]=contour(X,Y,Erms,[0:0.5:15]);
clabel(cs,h)
figure(4)
plot(x,y,'h')
hold on
plot(Mn(:,1),Mn(:,2),'o')
hold on
plot(Mn(:,1),Mn(:,2))
grid on
proses input data, disini terdapat data kecepatan Vp = 4 kemudian ada data longitude
dan lattitude pada masing-masing stasiun. Selanjutnya membuat meshgrid atau tebakan awal
untuk melakukan duplikat matriks X dan Matriks Y setelah itu dilakukan hubungan data
dengan parameter model dan juga dilakukan proses inversi. Pada proses inversi digunakan
turunan rumus dari fungsi pemodelan kedepan untuk memperoleh data perhitungan waktu tiba:
yang disesuaikan pada gempa arahnya memiliki secara horintal dan vertical. Sehingga akan
didapatkan matriks kernelnya.
Hasil waktu tiba dari perhitungan kemudian dibandingkan dengan hasil observasi untuk
mendapatkan delta T yang mana hal tersebut merupakan eror. Setelah itu jarak antara t hasil
perhitungan dengan t hasil observasi dilakukan minimumisasi.
Hasil Running dari script diatas berupa episenter dalam x dan y juga hasil perhitungan
objektif yang dinyatakan oleh kesalahan perhitungan rata-rata
Hasil akhirnya adalah
Kontur yang diperoleh merupakan hasil interpolarisasi hasil perhitungan objektif yang
disini merupakan selisih antara t observasi dengan t hasil perhitungan.Posisi episenter disitu
tidak tepat pada posisi parameter model hal tersebut terjadi akibat adanya penambahan erornya.