SAP Kalkulus Lanjut - Silabus Online IAIN Antasari Banjarmasin

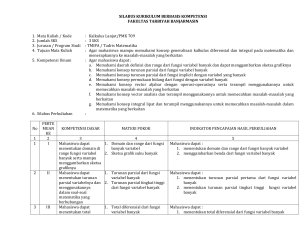
SILABUS KURIKULUM BERBASIS KOMPETENSI
FAKULTAS TARBIYAH BANJARMASIN
1.
2.
3.
4.
Mata Kuliah / Kode
Jumlah SKS
Jurusan / Program Studi
Tujuan Mata Kuliah
5. Kompetensi Umum
6. Silabus Perkuliahan
1
1
PERTE
MUAN
KE
2
I
2
II
3
III
No
: Kalkulus Lanjut/PMK 709
: 3 SKS
: TMIPA / Tadris Matematika
: Agar mahasiswa mampu memahami konsep generalisasi kalkulus diferensial dan integral pada matematika dan
menerapkannya ke masalah-masalah yang berkaitan
: Agar mahasiswa dapat :
a. Memahami daerah definisi dan range dari fungsi variabel banyak dan dapat menggambarkan sketsa grafiknya
b. Memahami konsep turunan parsial dari fungsi variabel banyak
c. Memahami konsep turunan parsial dari fungsi implicit dengan variabel yang banyak
d. Memahami konsep permukaan bidang dari fungsi dengan variabel banyak
e. Memahami konsep vector aljabar dengan operasi-operasinya serta terampil menggunakannya untuk
memecahkan masalah-masalah yang berkaitan
f. Memahami konsep vector analisis dan terampil menggunakannya untuk memecahkan masalah-masalah yang
berkaitan
g. Memahami konsep integral lipat dan terampil menggunakannya untuk memecahkan masalah-masalah dalam
matematika yang berkaitan
:
KOMPETENSI DASAR
3
Mahasiswa dapat
menentukan domain di
range fungsi variabel
banyak serta mampu
menggambarkan sketsa
grafiknya
Mahasiswa dapat
menentukan turunan
parsial variabelnya dan
menggunakannya
dalam soal-soal
matematika yang
berhubungan
Mahasiswa dapat
menentukan total
MATERI POKOK
4
1. Domain dan range dari fungsi
banyak variabel
2. Sketsa grafik suku banyak
INDIKATOR PENCAPAIAN HASIL PERKULIAHAN
5
Mahasiswa dapat :
1. menentukan domain dan range dari fungsi banyak variabel
2. menggambarkan benda dari fungsi variabel banyak
1. Turunan parsial dari fungsi
variabel banyak
2. Turunan parsial tingkat tinggi
dari fungsi variabel banyak
Mahasiswa dapat :
1. menentukan turunan parsial pertama dari fungsi variabel
banyak
2. menentukan turunan parsial tingkat tinggi fungsi variabel
banyak
1. Total diferensial dari fungsi
variabel banyak
Mahasiswa dapat :
1. menentukan total diferensial dari fungsi variabel banyak
4
IV
5
V
6
VI
7
VII
8
VIII
diferensial dari fungsi
variabel banyak dan
penggunaannya dalam
soal-soal matematika
yang berhubungan
Mahasiswa dapat
memahami konsep
fungsi implicit fungsi
variabel banyak dan
menentukan turunan
parsialnya
Mahasiswa dapat
memahami konsep
bidang singgung dan
garis normal, bidang
normal dan garis
singgung disuatu titik
pada permukaan dalam
ruang
Mahasiswa dapat
memahami konsep
vector aljabar dengan
operasi-operasinya dan
terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Mahasiswa dapat
memahami konsep
vector aljabar dengan
operasi-operasinya dan
terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Mahasiswa dapat
amemahami konsep
vector analisis, sifatsifatnya dan terampil
menggunakannya untuk
menyelesaikan soal-
2. Persamaan garis singgung
pada permukaan parabola di
suatu titik
3. Pendekatan suatu besaran
menggunakan total diferensial
Fungsi implicit fungsi variabel
banyak
2. menentukan persamaan garis singgung pada permukaan
parabola disuatu titik
Mahasiswa dapat menentukan turunan parsial dari fungsi implicit
variabel banyak
1. Garis singgung dan bidang
normal disuatu titik pada
kurva dalam ruang
2. Bidang singgung dan garis
normal disuatu titik pada
kurva dalam ruang
Mahasiswa dapat :
1. menentukan garis singgung dan bidang normal disuatu titik
2. menentukan bidang singgung dan garis normal disuatu titik
pada kurva dalam ruang
1. Konsep vector aljabar pada
bidang dan dalam ruang
2. Operasi-operasi vector aljabar
dengan sifat-sifatnya
Mahasiswa dapat :
1. menentukan suatu vector adalah vector aljabar pada bidang
atau ruang
2. menentukan hasil penjumlahan/pengurangan vector
3. menentukan hasil perkalian skalar dengan vector
4. menentukan hasil perkalian titik dan silang dari dua vector
5. menentukan hasil triple scalar product tiga buah vector
6. menentukan hasil triple vector product dari tiga buah vector
Mahasiswa dapat :
1. menentukan persamaan garis lurus yang melalui suatu titik
yang sejajar dengan suatu vector
2. menentukan jarak suatu titik terhadap titik lain atau terhadap
suatu garis
3. menentukan persamaan bidang yang melalui suatu titik dan
sejajar atau tegak lurus suatu bidang yang ditentukan
1. Garis lurus
2. Bidang
1. Turunan (diferensial) vector
2. Rumus-rumus turunan vector
3. Turunan parsial vector
Mahasiswa dapat :
1. menentukan turunan vector
2. menentukan turunan vector dengan menggunakan rumus
3. menentukan turunan tingkat tinggi dan turunan parsial dari
vector
9
IX
10
X
11
XI
12
XII
13
XIII
14
XIV
soal yang berkaitan
Mahasiswa dapat
amemahami konsep
vector analisis, sifatsifatnya dan terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Mahasiswa dapat
amemahami konsep
vector analisis, sifatsifatnya dan terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Mahasiswa dapat
amemahami konsep
vector analisis, sifatsifatnya dan terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Mahasiswa dapat
amemahami konsep
vector analisis, sifatsifatnya dan terampil
menggunakannya untuk
menyelesaikan soalsoal yang berkaitan
Memahami konsep
integral lipat dan
terampil
menggunakannya untuk
memecahkan masalahmasalah dalam
matematika yang
berkaitan
Memahami konsep
integral lipat dan
terampil
menggunakannya untuk
Diferensial geometri
Mahasiswa dapat :
1. menentukan unit vector T
2. menentukan kelengkungan suatu kurva dan jari-jarinya
3. vektor normal N
4. vektor binormal B dan torsi τ
1. Persamaan bidang osculasi,
bidang normal dan bidangbidang rectifying
2. Persamaan garis singgung,
persamaan normal utama dan
persamaan binormal
Mahasiswa dapat :
1. menentukan bidang osculasi, bidang normal dan bidang
rectifying dari suatu kurva
2. menentukan persamaan garis singgung, persamaan normal
utama dan persamaan binormal disuatu titik pada suatu kurva
1. Gradient
2. Divergenec
3. Carl
Mahasiswa dapat :
1. menentukan gradien suatu fungsi
2. menentukan divergent dari suatu vector
3. menentukan cure dari suatu vector
4. menentukan vector normal satuan dan persamaan bidang
singgung pada permukaan disuatu titik
Vector integrasi
Mahasiswa dapat :
1. menentukan nilai integrasi tertentu dari vector
2. menentukan nilai integrasi tertentu suatu vector pada suatu
kurva tertentu
Integral lipat dua
Mahasiswa dapat :
1. menentukan nilai integral lipat dua
2. menentukan nilai integral lipat dua untuk daerah yang dibatasi
oleh kurva
Integral lipat tiga
Mahasiswa dapat :
1. menentukan nilai integral lipat tiga
2. menantukan nilai integral lipat tiga untuk daerah tertutup yang
dibatasi oleh bidang-bidang yang ditentukan
memecahkan masalahmasalah dalam
matematika yang
berkaitan
7. Sistem Perkuliahan
: - Metode yang digunakan
- Bentuk Kegiatan
- Evaluasi
8. Referensi
: a. Buku Wajib :
1. Frank Ayres, 1972. Calculus 2/ed. Schaum's outline series
2. Louis Leithold, 1986, Kalkulus dan Ilmu Ukur Analitik (terjemahan M. Morgha). Jakarta. Bina Aksara. Jilid 3
3. Murray R. Spielgal, 1959. Vektor Analysis. Schaum's outline series
b. Buku Anjuran :
1. K. Martono, 1986. Kalkulus dan Ilmu Ukur Analitik. Bandung. Penerbit Angkasa
Banjarmasin,
Penyusun,