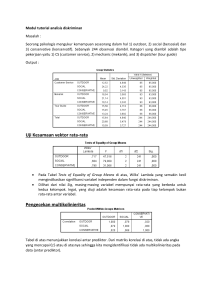
Tugas Persamaan Diferensial Numerik Metode Prediktor Korektor Oleh: Adinda Laili Febriyanti (02161001) Muhammad Hidayat (02161022) Nur Hanifa (02161025) Dosen Pengampu: Abrari Noor Hasmi, S.Si., M.Si. NIPH. 100118163 PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA DAN TEKNOLOGI KALIMANTAN INSTITUT TEKNOLOGI KALIMANTAN BALIKPAPAN 2019 Tinjauan Pustaka 1. Metode Prediktor Korektor Metode implisit Adams Moulton secara umum lebih akurat dibanding metode eksplisit Adams Bashfort. Metode implisit, tidak selalu bisa digunakan karena tidak semua fungsi bisa diselesaikan secara aljabar. Kombinasi metode eksplisit untuk memprediksi dan implisit untuk meningkatkan prediksi disebut metode predictor korektor. Metode Adam orde 4 adalah salah satu metode multistep yang didasarkan rumus integrasi adam dengan menggunakan rumus Adam Bashforth orde 4 sebagai prdiktor: 𝑤4𝑝 = 𝑤3 + ℎ [55𝑓(𝑡3 , 𝑤3 ) − 59𝑓(𝑡2 , 𝑤2 ) + 37𝑓(𝑡1 , 𝑤1 ) − 9𝑓(𝑡0 , 𝑤0 )] 24 Dan rumus Adam Moulton orde 4 sebagai korektor: 𝑤4 = 𝑤3 + ℎ [9𝑓(𝑡4 , 𝑤4𝑝 ) + 19𝑓(𝑡3 , 𝑤3 ) − 5𝑓(𝑡2 , 𝑤2 ) + 𝑓(𝑡1 , 𝑤1 )] 24 2. Metode Runge Kutta Orde 4 𝑘1 = ℎ𝑓(𝑡, 𝑤𝑖 ) ℎ 1 𝑘2 = ℎ𝑓(𝑡 + , 𝑤𝑖 + 𝑘1 ) 2 2 ℎ 1 𝑘3 = ℎ𝑓(𝑡 + , 𝑤𝑖 + 𝑘2 ) 2 2 𝑘4 = ℎ𝑓(𝑡 + ℎ, 𝑤𝑖 + 𝑘3 ) Sehingga diperoleh : 1 𝑤𝑖+1 = 𝑤𝑖 + (𝑘1 + 2𝑘2 + 2𝑘3 + 𝑘4 ) 6 Hasil dan Pembahasan Lakukan approksimasi solusi persamaan differensial di bawah ini: 𝑦 ′ = 𝑦 − 𝑡 2 + 1, 0 ≤ 𝑡 ≤ 2, 𝑦(0) = 0.5 Dengan menggunakan metode Prediktor-Korektor orde 4 dan Runge Kutta orde 4. Masingmasing dengan diskretisasi 2−2 , 2−3 , 2−4 , 2−5 . Bandingkan nilai hasil aproksimasi dengan solusi eksak: 𝑦(𝑡) = (𝑡 + 1)2 − 0.5𝑒 𝑡 Tentukan nilai error pada 𝑡 = 2. Metode manakah yang lebih akurat? Metode manakah yang waktu eksekusinya lebih cepat? Berapa banyak efisiensi waktu yang diperoleh? Solusi : - Dari kedua metode tersebut, yang lebih akurat adalah Metode Prediktor-Korrektor. Metode Runge Kutta Orde 4 memiliki efisiensi waktu sebesar 20.18421993225 sedangkan untuk Metode Prediktor Korektor memiliki efisiensi waktu sebesar 36.05339312553406. Sehingga Metode yang waktu eksekusinya lebih cepat adalah Runge Kutta Orde 4 yaitu 20.18421993225. Perbandingan nilai hasil aproksimasi dengan solusi eksak dapat dilihat pada tabel di bawah ini: Prediktor Korektor Orde 4 Tabel 1. Metode Prediktor Korektor Orde 4 dengan h=0.5 Tabel 2. Metode Prediktor Korektor Orde 4 dengan h=0.25 Tabel 3. Metode Prediktor Korektor Orde 4 dengan h=0.125 Tabel 4. Metode Prediktor Korektor Orde 4 dengan h=0.0625 Tabel 5. Metode Prediktor Korektor Orde 4 dengan h=0.01325 Tabel 6. Nilai Error dengan diskretisasi 2−1 , 2−2 , 2−3 , 2−4 , 2−5 Runge Kutta Orde 4 Tabel 7. Metode Runge Kutta Orde 4 dengan h=0.5 Tabel 8. Metode Runge Kutta Orde 4 dengan h=0.25 Tabel 9. Metode Runge Kutta Orde 4 dengan h=0.125 Tabel 10. Metode Runge Kutta Orde 4 dengan h=0.0625 Tabel 11. Metode Runge Kutta Orde 4 dengan h=0.01325 Tabel 12. Nilai Error dengan diskretisasi 2−1 , 2−2 , 2−3 , 2−4 , 2−5 Lampiran 1 (Metode Prediktor Korektor) Lampiran 2 (Metode Runge Kutta)