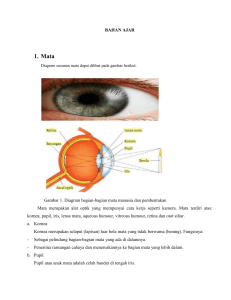
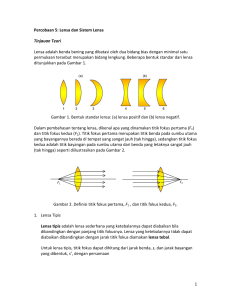
Bab II - hierofredy

.
FISIKA KELAS XI
BAB X
OPTIKA GEOMETRIK
Cahaya merupakan bentuk energi gelombang yang sangat vital bagi manusia. Coba
kamu bayangkan hidup tanpa cahaya, dimana sekeliling kita gelap gulita tanpa ada
cahaya matahari, cahaya lampu ataupun cahaya api. Dalam waktu singkat peradaban
manusia tak mampu bertahan lama. Manusia akan punah. Untunglah cahaya telah ada
sejak dahulu, sehingga manusia dapat memanfatkan cahaya berdasar sifat-sifat
geometrk cahaya seperti pemantulan, pembiasan dan sebagainya. Mata, kacamata dan
berbagai peralatan yang menggunakan lensa maupun prisma banyak membantu
pekerjaan manusia Alat-alat itu disebut sebagai alat optik.
Alat-alat optik mampu menutupi keterbatasan indera penglihatan manusia yang tidak
mampu melihat dengan jelas benda-benda yang jauh, benda-benda yang sangat kecil.
Dengan bantuan cahaya dan alat optik manusia dapat merekam kejadian-kejadian yang
telah berlalu. Dalam bab ini kamu akan diajak memperdalam tentang cahaya dan alatalat optik serta penerapannya dalam kehidupan sehari-hari.
260
.
Tujuan Pembelajaran




Menerapkan pemantulan cahaya pada cermin datar dan cermin lengkung
Menerapkan pembiasan cahaya pada lensa, balok kaca dan prisma
Menerapkan prinsip kerja alat-alat optik dalam kehidupan sehari-hari
Menerapkan persamaan pada tiap-tiap alat optik dalam persoalan
Standar Kompetensi
 Menerapkan prinsip kerja alatalat optik
Kompetensi Dasar
 Menganalisis alat-alat optik
secara kualitatif dan kuantitatif
 Menerapkan alat-alat optik
dalam kehidupan sehari-hari
Pernahkah kamu difoto menggunakan kamera? Pernahkah kamu melihat jarak jauh
menggunakan teropong prisma (keker)? Pernahkah kamu melihat benda kecil
menggunakan lup atau mikroskop? Tetapi pasti jarang diantara kamu melihat pulau dari
dalam kapal selam menggunakan periskop. Untuk melihat benda-benda yang sangat
kecil seperti mikroorganisme, sel darah, kamu membutuhkan alat bantu mikroskop.
Demikian juga kalau kita mau mengamati benda-benda yang sangat jauh seperti
bintang, rasi bintang, bulan dan lain sebagainya kita membutuhkan teleskop.Alat-alat
tersebut dan alat-alat lainnya yang menggunakan lensa dan prisma tergolong sebagai
alat-alat optik. Dalam bab ini akan dibahas banyak hal tentang alat-alat tersebut. Namun
sebelumnya Kamu harus memahami lebih banyak apa itu cahaya.
261
.
Peta Konsep Bab 10
CAHAYA
(OPTIK)
OPTIK FISIS
ALATALAT
OPTIK
OPTIK GEOMETRIS
PEMANTULAN CAHAYA
CERMIN
MATA DAN KACA MATA
KAMERA
PEMBIASAN CAHAYA
LUP
MIKROSKOP
LENSA
KACA PLAN
PARALEL
TELESKOP
PRISMA
262
.
A. Cahaya
1. Pemantulan Cahaya
Seseorang dapat melihat benda karena benda tersebut mengeluarkan atau
memantulkan cahaya ke mata kita. Karena ada cahaya dari benda ke mata kita, entah
cahaya itu memang berasal dari benda tersebut, entah karena benda itu memantulkan
cahaya yang datang kepadanya lalu mengenai mata kita. Jadi, gejala melihat erat
kaitannya dengan keberadaan cahaya atau sinar.
Cabang fisika yang mempelajari cahaya yang meliputi bagaimana
terjadinya cahaya, bagaiamana perambatannya, bagaimana pengukurannya dan
bagaimana sifat-sifat cahaya dikenal dengan nama Optika. Dari sini kemudian dikenal
kata optik yang berkaitan dengan kacamata sebagai alat bantu penglihatan. Optika
dibedakan atas optik geometri dan optik fisik .
Pada optik geometri dipelajari sifat-sifat cahaya dengan menggunakan
alat-alat yang ukurannya relatif lebih besar dibandingkan dengan panjang gelombang
cahaya. Sedangkan pada optik fisik cahaya dipelajari dengan menggunakan alat-alat yang
ukurannya relatif sama atau lebih kecil dibanding panjang gelombang cahaya sendiri.
Cahaya selalu merambat lurus seperti yang terlihat manakala cahaya
matahari menerobos dedaunan. Sehingga cahaya yang merambat digambarkan sebagai
garis lurus berarah yang disebut sinar cahaya, sedangkan berkas cahaya terdiri dari
beberapa garis berarah. Berkas cahaya bisa parallel z, divergen (menyebar) atau
konvergen (mengumpul).
Seorang ahli matematika berkebangsaan belanda yang bernama Willebrod
Snellius (1591 – 1626) dalam penelitiannya ia berhasil menemukan hukum pemantulan
cahaya yang berbunyi :
1. Sinar datang, sinar pantul dan garis normal terletak pada satu bidang datar.
2. Sudut sinar datang sama dengan sudut sinar pantul.
263
.
Gambar 1. Diagram pemantulan cahaya,
dengan keterangan (1) garis normal, (2)
sinar datang, dan (3) sinar pantul. Sudut b
adalah sudut datang, sudut c adalah sudut
pantul.
Secara garis besar pemantulan cahaya terbagi menjadi dua yaitu
pemantulan teratur dan pemantulan baur (pemantulan difus). Pemantulan teratur terjadi
jika berkas sinar sejajar jatuh pada permukaan halus sehingga berkas sinar tersebut akan
dipantulkan sejajar dan searah, sedangkan pemantulan baur terjadi jika sinar sejajar jatuh
pada permukaan yang kasar sehingga sinar tersebut akan dipantulkan ke segala arah.
Pada permukaan benda yang rata seperti cermin datar, cahaya dipantulkan
membentuk suatu pola yang teratur. Sinar-sinar sejajar yang datang pada permukaan
cermin dipantulkan sebagai sinar-sinar sejajar pula. Akibatnya cermin dapat membentuk
bayangan benda. Pemantulan semacam ini disebut pemantulan teratur atau pemantulan
biasa .
Berbeda dengan benda yang memiliki permukaan rata, pada saat cahaya
mengenai suatu permukaan yang tidak rata, maka sinar-sinar sejajar yang datang pada
permukaan tersebut dipantulkan tidak sebagai sinar-sinar sejajar. Pemantulan seperti ini
disebut pemantulan baur. Akibat pemantulan baur ini manusia dapat melihat benda dari
berbagai arah. Misalnya pada kain atau kertas yang disinari lampu sorot di dalam ruang
gelap, dapat terlihat apa yang ada pada kain atau kertas tersebut dari berbagai arah.
Pemantulan baur yang dilakukan oleh partikel-partikel debu di udara yang berperan
dalam mengurangi kesilauan sinar matahari.
a. Pemantulan pada Cermin Datar
Cermin memantulkan hampir semua sinar yang datang kepadanya. Di
masa lalu cermin dibuat dari kaca yang dilapisi perak. Dewasa ini banyak cermin dibuat
dengan cara melapisi suatu benda yang telah digosok hingga halus dengan alumunium
yang diuapkan di ruang hampa di atas alumunium dilapisi silikon monooksida agar tidak
mudah berkarat. Cermin juga dapat dibuat dari logam yang permukaannya digosok
264
.
hingga mengkilap. Dibandingkan cermin dari kaca, cermin ini lebih awet sebab tidak
mudah pecah. Hanya saja cermin menjadi lebih berat.
Cermin datar adalah cermin yang bentuk permukaannya datar. Di
rumahmu pasti memiliki cermin datar yang digunakan setiap hari untuk bercermin.
Sekarang cobalah kamu bercermin di depan cermin tersebut! Apa yang terjadi?
Perhatikan bayanganmu di cermin tersebut! Besarnya bayangan yang ada di cermin tidak
berubah sama sekali masih sama dengan besar kamu yang sesungguhnya, demikian juga
jarakmu ke cermin juga sama dengan jarak bayangan ke cermin. Sekarang ambilah kertas
kemudian tulis namamu di atas kertas tersebut kemudian hadapkan tulisan tersebut
menghadap cermin. Perhatikan tulisan yang ada di kertas! Kamu akan mendapatkan
kesan bahwa tulisan tersebut terbalik seolah-olah posisi sebelah kanan menjadi kiri.
Dari percobaan ini dapat kita simpulkan bahwa cermin datar akan
membentuk bayangan dengan sifat-sifat maya, sama tegak dengan benda aslinya dan
sama besar dengan benda aslinya.
1) Melukis Pembentukan Bayangan Pada Cermin Datar
Untuk melukis bayangan pada cermin datar menggunakan hukum
pemantulan cahaya. Misalkan saja Anda hendak menentukan bayangan benda O
sebagaimana terlihat pada gambar 2. Sinar datang dari O ke cermin membentuk sudut
datang (i) , di titik tersebut ada garis normal tegak yang lurus permukaan cermin. Dengan
bantuan busur derajat, ukurlah besar sudut datang (i) yakni sudut yang dibentuk oleh
sinar datang dengan garis normal. Ukurlah sudut pantul (r) yaitu sudut antara garis
normal dan sinar pantul yang besarnya sama dengan sudut datang. Posisi bayangan dapat
ditentukan dengan memperpanjang sinar pantul D melalui C hingga ke O' yang
berpotongan dengan garis OO' melalui B.
Gambar 2.a. Melukis
pembentukan
bayangan sebuah
benda titik pada
cermin datar.
265
.
Gambar 2.b. Melukis
pembentukan bayangan
sebuah benda garis pada
cermin datar.
2) Menggabung Dua Cermin Datar
Dua buah cermin datar yang digabung dengan cara tertentu dapat
memperbanyak jumlah bayangan sebuah benda. Jumlah bayangan yang terjadi
bergantung pada besar sudut yang dibentuk oleh kedua cermin itu. Jika kamu memiliki
dua buah cermin segi empat lakukanlah percobaan berikut. Letakkan kedua cermin
tersebut saling berhadapan dengan salah satu sisi segi empat tersebut berhimpit hingga
membentuk sudut 900, kemudian letakkanlah sebuah benda P (pensil misalnya) diantara
kedua cermin tersebut! Perhatikanlah berapa jumlah bayangan yang terbentuk?
Gambar 3. Dua cermin datar A dan B yang
dipertemukan kedua ujungnya membentuk
sudut 90 satu sama lain dapat memantulkan
cahaya dari benda P hingga membentuk tiga
buah bayangan A’, B’, dan A”= B”
Ubahlah sudut cermin hingga membentuk sudut 600, berapakah jumlah
bayangan yang terbentuk sekarang? Hitunglah seluruh bayangan pensil yang tampak di
permukaan kedua cermin A maupun B. Ternyata sebanyak lima bayangan.
266
.
Gambar 4. Dengan mempertemukan
dua permukaan sermin A dan B di
titik C membentuk sudut apit sebesar
60 menghasilkan jumlah bayangan
sebanyak lima buah.
Bila sudut antara dua cermin datar 90 menghasilkan 3 bayangan dari
suatu benda yang diletakkan di antara kedua cermin tersebut dan sudut 60° menghasilkan
5 bayangan, berapakah jumlah bayangan yang dibentuk bila sudut antara dua cermin 30° ,
22,5° , 15° dan seterusnya?
Ternyata jika sudut kedua cermin diubah-ubah (0<α<900) jumlah
bayangan benda juga akan berubah-ubah sesuai dengan persamaan empiris
n
360

1
dengan :
n
: Jumlah bayangan
α
: sudut antara kedua cermin
Penggunaan gabungan dua cermin datar dapat Kamu jumpai misalnya di
toko sepatu atau toko pakaian dan digunakan oleh para pelanggan toko tersebut saat
mencoba sepatu atau pakaian yang hendak mereka beli. Gabungan dua cermin ini dapat
juga kamu temui di salon-salon kecantikan, di tempat fitness centre, atau di rumah main
bagi kanak-kanak.
Tugas
Kerjakan di buku tugasmu!
267
.
Berapakah jumlah bayangan dari suatu benda yang dapat dibentuk oleh dua cermin datar
yang digabung berhadapan dengan sudut antara dua cermin itu (a) 24° (b) 45° (c) 120 ?
3) Tinggi Minimal Cermin Datar Agar Saat Bercermin Seluruh Bayangan Tubuh
Tampak di dalam Cermin
Bila seorang anak yang tingginya 150 cm ingin melihat bayangannya pada
cermin datar, haruskah cermin itu mempunyai tinggi yang sama dengan anak itu?
Gambar
5.
Panjang
minimal cermin yang
diperlukan agar bayangan
anak tampak seluruhnya
dari ujung kaki sampai
ujung rambut di dalam
cermin adalah cukup L =
½ h, dimana h sebagai
tinggi
badan
anak
tersebut.
Bila d = jarak mata ke ujung rambut (m), L = tinggi minimal cermin datar
yang diperlukan (m), h = tinggi orang dari ujung kaki sampai ujung rambut (m), maka
diperoleh hubungan bahwa L = ½ h. Jadi, agar dapat melihat tinggi seluruh bayangan
benda pada sebuah cermin datar maka tinggi cermin itu haruslah sama dengan setengah
tinggi badan. Sedangkan pemasangan bagian bawah cermin haruslah ½ jarak ujung jari
kaki ke mata.
Bagaimana dengan jarak orang ke cermin datar, apakah berpengaruh
dalam pembentukan bayangan? Jawabnya tidak. Perubahan jarak badan dari cermin datar,
hanya merubah besar sudut datang (i). Akan tetapi karena sudut pantul (r) selalu sama
dengan sudut datang (i), maka besar sudut-sudut pantul akan berubah sesuai dengan
perubahan besar sudut-sudut datang sehingga tidak merubah bayangan yang terbentuk.
268
.
Tugas
Kerjakan di buku tugasmu!
Seseorang yang memiliki tinggi dari ujung kaki sampai ke matanya 150 cm berdiri di
depan cermin datar pada jarak 1,5 m. Cermin itu ditegakkan vertikal di atas meja. Jarak
dari mata ke ujung kepala 10 cm. Berapakah tinggi meja dari lantai, dan berapa tinggi
vertikal cermin?
b. Pemantulan pada Cermin Sferik (Lengkung)
Cermin sferik adalah cermin lengkung seperti permukaan lengkung sebuah
bola dengan jari-jari kelengkungan R. Cemin ini dibedakan atas cermin cekung (konkaf)
dan cermin cembung (konveks). Setiap cermin sferik baik itu cermin cekung ataupun
cermin cembung memiliki fokus f yang besarnya setengah jari-jari kelengkungan cermin
tersebut.
f 
R
2
dengan
f
: jarak fokus
R
: jari-jari kelengkungan cermin
Bagian-bagian cermin lengkung antara lain adalah sumbu utama (C-O),
titik pusat kelengkungan cermin ( C ), titik pusat bidang cermin ( O ), jari-jari
kelengkungan cermin ( R ), titik fokus / titik api ( F ) , jarak fokus (f) dan bidang fokus .
Gambar 6 Bagian-bagian pada cermin (a) cermin cekung, (b) cermin cembung
269
.
Garis pada cermin sferik yang menghubungkan antara pusat kelengkungan C, titik fokus
f dan titik tengah cermin O disebut sumbu utama.
Menurut dalil Esbach jarak antara dua titik tertentu pada cermin cekung
dapat diberi nomor-nomor ruang. Jarak sepanjang OF diberi nomor ruang I, sepanjang FC
diberi nomor ruang II, lebih jauh dari C diberi nomor ruang III dan dari O masuk ke
dalam cermin diberi nomor ruang IV. Ruang I sampai III ada di depan cermin cekung
(daerah nyata) dan ruang IV ada di belakang cermin cekung (daerah maya).
Gambar 7. Penomoran ruang pada cermin
cekung. Daerah di depan cermin disebut
daerah nyata, dan daerah di belakang
cermin disebut daerah maya.
Pada cermin cekung semua cahaya yang datang sejajar sumbu utama akan difokuskan
sesuai dengan sifatnya yaitu mengumpulkan cahaya. Titik berkumpulnya sinar-sinar
pantul disebut titik fokus atau titik api yang terletak di sumbu utama. Cara melukis sinarsinar pantulnya tetap menggunakan hukum pemantulan cahaya.
Gambar 8. Pemantulan berkas
cahaya sejajar sumbu utama pada
cermin cekung
Bagaimana jika sinar-sinar yang datang ke cermin cekung tidak sejajar
sumbu utama? Ternyata berkas-berkas sinar pantul akan berpotongan di satu titik yang
tidak terletak pada sumbu utama. Oleh cermin sinar-sinar tersebut akan dipantulkan tidak
melalui fokus melainkan melewati suatu titik tertentu pada bidang fokus utama seperti
tampak pada gambar 8.
270
.
Gambar 9. Pemantulan berkas
cahaya yang datangnya tidak
sejajar sumbu utama pada
cermin cekung
1) Pembentukan bayangan oleh cermin cekung
Untuk menggambarkan bagaimana terbentuknya bayangan pada cermin
cekung dapat menggunakan bantuan sinar-sinar istimewa, dengan demikian lukisan
bayangan akan dapat dilukis dengan mudah karena sinar-sinar tersebut mudah diingat
ketentuannya tanpa harus mengukur sudut datang dan sudut bias. Sinar-sinaar istimewa
inipun tetap berdasarkan hukum pemantulan cahaya. Untuk menggambarkan bagaimana
terbentuknya bayangan pada cermin sferik kita dapat menggunakan bantuan sinar-sinar
istimewa, dengan demikian lukisan bayangan akan dapat kita lukis dengan mudah.
Sinar-sinar istimewa pada cermin cekung adalah sebagai berikut:
1. Sinar yang datang sejajar sumbu utama dipantulkan melalui titik fokus (F).
Gambar 10. Sinar yang sejajar
sumbu utama akan dipantulkan
cermin cekung melalui titik fokus
2. Sinar yang datang melalui titik fokus (F) akan dipantulkan sejajar sumbu utama.
Gambar 11. Sinar yang melalui
fokus akan dipantulkan cermin
cekung sejajar sumbu utama
3. Sinar-sinar yang datang melalui pusat kelengkungan ( C ) akan dipantulkan kembali
melalui titik pusat kelengkungan tersebut.
271
.
Gambar 12. Sinar yang melewati
titik pusat kelengkungan cermin
akan dipantulkan cermin cekung
melewati titik tersebut.
Contoh melukis bayangan pada cermin cekung

Benda berada di jauh tak terhingga
Sinar-sinar yang berasal dari benda yang jauh
tak terhingga datang ke cermin berupa sinarsinar sejajar dan oleh cermin sinar-sinar ini
akan dikumpulkan di fokus utama sehingga
bayangan benda yang terbentuk berupa titik di
titik fokus cermin.

Benda berada di titik pusat kelengkungan cermin (titikC)
Benda AB berada di titik pusat
kelengkungan cermin cekung akan
menghasilkan bayangan yang tepat
berada di titik pusat kelengkungan
cermin
pula. Dapatkah kamu
menyebutkan sifat-sifat bayangan
yang terbentuk ?

Benda berada di ruang II
Benda AB berada di ruang II cermin
cekung akan menghasilkan bayangan
di
ruang
III.
Sebutkan
bayangan yang terbentuk !
272
sifat-sifat
.

Benda berada di ruang III
Benda AB terletak di ruang III cermin
cekung akan menghasilkan bayangan
di ruang II. Cobalah kamu sebutkan
sifat-sifat bayangan yang terbentuk !

Benda berada di titik fokus
Benda AB tepat di titik fokus maka sinarsinar yang datang dari benda dipantulkan
oleh cermin cekung sejajar sumbu utama
sehingga tidak terbentuk bayangan, atau
sering juga dikatakan bahwa bayangan
benda berada di jauh tak terhingga.

Benda berada di ruang I
273
.
Bila benda berada di ruang I,
bayangan
yang
terbentuk
merupakan perpotongan dari
perpanjangan
pantul,
sehingga
sinar-sinar
bayangan
berada di belakang cermin.
Dari contoh-contoh tersebut dapat disimpulkan bahwa antara ruang tempat benda berada
dan tempat bayangan berada bila dijumlah hasilnya adalah 5. Kecuali benda yang berada
di titik-titik khusus. Dengan demikian berlaku:
Nomor ruang benda + nomor ruang bayangan = 5
Tugas
Kerjakan di buku tugasmu!
Lukislah pembentukan bayangan dari benda AB yang berada di dalam ruang IV cermin
cekung. Sebutkan pula sifat-sifatnya!
2) Pembentukan Bayangan Oleh Cermin Cembung
Sama halnya dengan cermin cekung, pada cermin cembung juga
mempunyai tiga macam sinar istimewa. Karena jarak fokus dan pusat kelengkungan
cermin cembung berada di belakang cermin maka ketiga sinar istimewa pada cermin
cembung tersebut adalah :
1. Sinar yang datang sejajar dengan sumbu utama akan dipantulkan seolah-olah berasal
dari titik fokus (F).
Gambar 13. Sinar yang datang sejajar sumbu
utama akan dipantulkan seolah-olah dari titik
fokus
274
.
2. Sinar yang datang menuju titik fokus (F) akan dipantulkan sejajar sumbu utama.
Gambar 14. Sinar yang datang seolah-olah
menuju fokus akan di pantulkan sejajar sumbu
utama
3. Sinar-sinar yang menuju titik pusat kelengkungan ( C ) akan dipantulkan seolah-olah
berasal dari titik pusat kelengkungan tersebut.
Gambar 15. Sinar yang datang menuju pusat
kelengkungan akan dipantulkan kembali
melalui sinar itu juga.
Contoh melukis bayangan pada cermin cembung
Seperti halnya pada cermin cekung, melukis bayangan pada cermin cembung juga
diperlukan minimal dua sinar istimewa. Karena depan cermin adalah ruang IV maka
berapapun jarak benda nyata dari cermin tetap berada di ruang IV . Dengan demikian
bayangan yang terbentuk berada di ruang I cermin cembung dan bersifat maya,
diperkecil.
Gambar
16.
Proses
pembentukan bayangan pada
cermin cembung. Bayangan
dari benda nyata selalu di
ruang I cermin, bersifat maya,
diperkecil dan sama tegak
dengan bendanya.
275
.
Itulah sebabnya bayangan yang terlihat di dalam kaca spion dari benda-benda nyata di
depan kaca spion tampak mengecil dan spion mampu mengamati ruang yang lebih luas.
Tugas
Kerjakan di buku tugasmu!
Lukislah pembentukan bayangan dari benda AB yang berada di dalam ruang I, II, dan III
cermin cembung. Sebutkan pula sifat-sifatnya!
Ketentuan Sifat-sifat Bayangan oleh Cermin Lengkung
Selain dengan cara melukis secara cepat kamu dapat menentukan sifatsifat bayangan yang dibentuk oleh cermin-cermin sferik dengan menggunakan ketentuanketentuan berikut :
-
Jumlah nomor ruang benda dan nomor ruang bayangan selalu sama dengan lima
-
Benda yang terletak di ruang II dan III selalu menghasilkan bayangan yang
terbalikterhadap bendanya. Sedangkan benda-benda yang berada di ruang I dan
IV akan selalu menghasilkan bayangan yang sama tegak dengan bendanya.
-
Jika nomor ruang bayangan lebih besar daripada nomor ruang benda, bayangan
selalu lebih besar daripada bendanya (diperbesar).
-
Jika nomor ruang bayangan lebih kecil daripada nomor ruang benda, bayangan
selalu lebih kecil daripada bendanya (diperkecil).
3) Hubungan antara Jarak Benda, Jarak Fokus dan Jarak Bayangan
Hubungan antara jarak benda (s), jarak fokus (f) dan jarak bayangan (s’)
pada cermin cekung dapat ditentukan dengan bantuan geometrik.
Gambar 17. Hubungan antara jarak
benda (s), jarak bayangan (s’), dan
jarak fokus (f) dalam ukuran
geometri.
276
.
Perhatikan perbandingan-perbandingan geometri dan trigonometri dari gambar 17
tersebut di atas. Jarak AB ke O adalah jarak benda (s), jarak A’B’ ke cermin adalah jarak
bayangan (s’) dan jarak F ke O adalah jaraak fokus (f). Pada gambar tersebut tampak
bahwa segitiga GFO dan A'B'F sebangun sehingga berlaku,
A' B' A' F

GO
FO
sehingga
h' s'-f

h
f
Pada gambar tampak juga bahwa segitiga ABO dan A'B'O sebangun sehingga diperoleh,
A' B' OA'

AB
OA
sehingga
h' s'

. Substitusikan kedua persamaan sehingga
h s
diperoleh persamaan
s' s'-f

, gunakan perkalian silang sehingga,
s
f
s’.f = s.s’ – s.f
Bagilah semua ruas dengan ss'f, akhirnya diperoleh :
1 1 1
 
s f s'
atau
1 1 1
 
f s s'
Bila jarak fokus sama dengan separuh jarak pusat kelengkungan cermin f = ½ R,
sehingga persamaan cermin lengkung juga dapat dituliskan dalam bentuk sebagai berikut
277
.
2 1 1
 
R s s'
Dalam menggunakan persamaan tersebut perlu diperhatikan kesepakatan tanda yang telah
disepakati bersama yaitu :
a. Jarak benda s bernilai positif (+) jika benda nyata terletak di depan cermin.
Jarak benda s bernilai negatif (-) jika benda maya terletak di belakang cermin.
b. Jarak bayangan s’ bernilai positif (+) jika bayangan nyata di depan cermin.
Jarak bayangan s’ bernilai negatif (-) jika bayangan maya di belakang cermin.
c. R dan f bertanda positif (+) untuk cermin cekung dan bertanda (-) untuk cermin
cembung.
Berbeda dengan cermin datar besar bayangan yang dibentuk oleh cermin
lengkung berbeda-beda sesuai dengan letak benda tersebut terhadap cermin. Untuk
mengetahui perbesaran linier pada pembentukan bayangan pada cermin lengkung maka
dapat dibandingkan tinggi bayangan h’ dengan tinggi benda h atau jarak bayangan
terhadap cermin s’ dengan jarak benda terhadap cermin s.
M 
h'
s'

h
s
dengan
M
: perbesaran linier
h’
: tinggi bayangan
h
: tinggi benda
s’
: jarak bayangan terhadap cermin
s
: jarak benda terhadap cermin
Jika dalam penghitungan ternyata diperoleh M >1 artinya bayangan yang dibentuk lebih
besar daripada bendanya, jika M = 1 maka bayangan sama besar dengan bendanya
sedangkan jika 0<M<1 maka bayangan yang dibentuk akan lebih kecil dari bendanya.
Contoh Soal:
278
.
1. Sebuah benda terletak 5 cm di depan sebuah cermin cekung yang berjari-jari 20
cm. Tentukan
a. jarak bayangan
b. Perbesaran bayangan
c. sifat-sifat bayangan!
Penyelesaian:
Diketahui : s = 5 cm
R = 20 cm maka f = 10 cm
Ditanya :
a. s’
b. M
c. sifat-sifat bayangan
Jawab:
a.
1 1 1
 
f s s'
1 1 1
 
10 5 s '
1 1 1


s' 10 5
1
1
2


s' 20 10
1
1

s'
10
sehingga
s’ =  10 cm
Jadi jarak bayangannya 10 cm
b. M =
s' 10

 2 kali
s
5
c. Sifat-sifat bayangannya adalah : maya, tegak, diperbesar, di ruang IV.
Tugas
279
.
Buatlah penyelesaian soal-soal berikut di buku tugasmu!
1.
Sebuah benda yang tingginya 4 cm diletakkan 15 cm di depan cermin cekung
dengan jari-jari kelengkungan 20 cm. Tentukan (a) jarak bayangan (b) tinggi
bayangan (c) sifat-sifat bayangan yang terbentuk!
2.
Sebuah benda yang tingginya 12 cm diletakkan 10 cm di depan cermin cembung
yang jari-jari kelengkungannya 30 cm. Tentukan (a) jarak bayangan (b) tinggi
bayangan (c) sifat-sifat bayangan
3.
Di manakah sebuah benda diletakkan di depan sebuah cermin cekung yang jarijari kelengkungannya 60 cm, agar bayangan yang dibentuk cermin itu bersifat
nyata dan berukuran 3 kali ukuran bendanya?
4.
Dua cermin cekung A dan B yang masing-masing berjari-jari 40 cm disusun
saling berhadapan dengan sumbu utama dan pusat kelengkungannya berhimpit.
Sebuah benda diletakkan 25 cm di depan cermin A. Tentukan (a) jarak bayangan
benda yang dibentuk oleh cermin A (b) jarak bayangan benda yang dibentuk oleh
cermin B (c) perbesaran bayangan total!
Kegiatan Percobaan
Tujuan :
Menentukan hubungan antara jarak benda, jarak bayangan, dan jarak fokus.
Alat dan Bahan
1 = bungku optik
2 = cermin cekung
3 = lilin sebagai benda
4 = karton putih sebagai layar
Petunjuk Teknis
280
.
1.
Susunlah alat-alat seperti tampak pada gambar. Atur posisi cermin dan lilin pada
jarak tertentu (s). Upayakan agar terbentuk bayangan pada layar dengan cara
mengeser-geser layar dibelakang cermin.
2.
Carilah bayangan lilin yang terlihat paling terang di layar lalu ukur jarak dari lilin
ke layar. itulah jarak bayangan (s').
3.
Amati bayangan api lilin pada layar apakah tegak atau terbalik, diperbesar atau
diperkecil.
4.
Lakukan langkah-langkah di atas untuk jarak benda yang berbeda-beda lalu catat
hasil pengamatanmu ke dalam tabel .
Latihan
Kerjakan persoalan berikut di buku latihanmu!
1. Lukislah bayangan sebuah benda yang tingginya 5 cm saat diletakkan 10 cm di depan
cermin cekung yang jari-jari kelengkungannya 20 cm!
2. Sebuah benda diletakkan 8 cm di depan cermin cekung yang jari-jari
kelengkungannya 22 cm. Tentukan sifat-sifat bayangan yang dibentuk oleh cermin
itu!
3. Sebuah cermin cekung mempunyai jari-jari kelengkungan 5 cm. Bila sebuah benda
diletakkan 2 cm di depan cermin itu, tentukanlah (a) jarak bayangan (b) perbesaran
bayangan dan (c) sifat-sifat bayangan yang terbentuk!
4. Sebuah benda yang tingginya 4 cm diletakkan 30 cm di depan cermin cekung yang
jari-jari kelengkungannya 20 cm. Tentukan (a) posisi bayangan (b) tinggi bayangan
dan (c) sifat-sifat bayangan!
5. Sebuah lilin setinggi 8 cm berada 6 cm di depan cermin cembung yang jarak
fokusnya 20 cm. Tentukan tinggi bayangan dan sifat-sifat bayangan yang terbentuk!
6. Dua cermin cekung A dan B dengan jarak fokus sama yakni 8 cm disusun berhadapan
dengan sumbu utama berhimpit satu sama lain. Jarak antara kedua cermin tersebut 52
281
.
cm. Suatu benda diletakkan pada jarak 10 cm di depan cermin A. Anggap sinar
datang dari benda ke cermin A terlebih dahulu baru dipantulkan ke cermin B.
Tentukan:
(a) perbesaran bayangan oleh cermin A
(b) perbesaran yang dilakukan oleh cermin B
(c) perbesaran total bayangan yang dibentuk oleh kedua cermin A dan B!
2. Pembiasan Cahaya
Pembiasan cahaya berarti pembelokan arah rambat cahaya saat melewati
bidang batas dua medium tembus cahaya yang berbeda indeks biasnya. Pembiasan
cahaya mempengaruhi penglihatan pengamat. Contoh yang jelas adalah bila sebatang
tongkat yang sebagiannya tercelup di dalam kolam berisi air dan bening akan terlihat
patah.
a. Indeks Bisa Medium
Ketika kamu sedang minum es pernahkah kamu memperhatikan sedotan
yang ada pada gelas es ? Sedotan tersebut akan terlihat patah setelah melalui batas antara
udara dan air. Hal ini terjadi karena adanya peristiwa pembiasan atau refraksi cahaya.
Bagaimana sebenarnya peristiwa ini terjadi?
Kecepatan merambat cahaya pada tiap-tiap medium berbeda-beda
tergantung pada kerapatan medium tersebut. Perbandingan perbedaan kecepatan rambat
cahaya ini selanjutnya disebut sebagai indeks bias. Dalam dunia optik dikenal ada dua
macam indeks bias yaitu indeks bias mutlak dan indeks bias relatif. Indeks bias mutlak
adalah perbandingan kecepatan cahaya di ruang hampa dengan kecepatan cahaya di
medium tersebut
n medium 
c
v
dengan
nmedium : indeks bias mutlak medium
c
: cepat rambat cahaya di ruang hampa
282
.
v
: cepat rambat cahaya di suatu medium
Indeks bias mutlak medium yaitu indeks bias medium saat berkas cahaya
dari ruang hampa melewati medium tersebut. Indek bias mutlak suatu medium dituliskan
nmedium. Indeks bias mutlak kaca dituliskan nkaca, indeks bias mutlak air dituliskan nair dan
seterusnya. Oleh karena c selalu lebih besar dari pada v maka indeks bias suatu medium
selalu lebih dari satu nmedium >1.
Contoh indeks bias mutlak beberapa zat.
Medium
Indeks bias mutlak
Udara (1 atm, 0° C)
1,00029
Udara (1 atm, 0° C)
1,00028
Udara (1 atm, 0° C)
1,00026
Air
1,33
Alkohol
1,36
Gliserin
1,47
Kaca kuarsa
1,46
1,52
Kaca kerona
1,65
Kaca flinta
2,42
Intan
Indeks bias relatif adalah perbandingan indeks bias suatu medium terhadap
indeks bias medium yang lain.
n12 
n1
n2
atau
n 21 
n2
n1
dengan
n12
: indeks bias relatif medium 1 terhadap medium 2
n21
: indeks bias relatif medium 2 terhadap medium 1
n1
: indeks bias mutlak medium 1
n2
: indeks bias mutlak medium 2
283
.
Setiap medium memiliki indeks bias yang berbeda-beda, karena perbedaan
indeks bias inilah maka jika ada seberkas sinar yang melalui dua medium yang berbeda
kerapatannya maka berkas sinar tersebut akan dibiaskan. Pada tahun 1621 Snellius,
seorang fisikawan berkebangsaan Belanda melakukan serangkaian percobaan untuk
menyelidiki hubungan antara sudut datang (i) dan sudut bias (r). Hukum pembiasan
Snellius berbunyi:
1. Sinar datang, sinar bias dan garis normal terletak pada satu bidang datar.
2. Perbandingan sinus sudut datang dengan sinus sudut bias dari suatu cahaya yang
melewati dua medium yang berbeda merupakan suatu konstanta.
sin i n2

sin r n1
Menurut teori muka gelombang rambatan cahaya dapat digambarkan sebagai muka
gelombang yang tegak lurus arah rambatan dan muka gelombang itu membelok saat
menembus bidang batas medium 1 dan medium 2 seperti diperlihatkan gambar 18.
Cahaya datang dengan
sudut i dan dibiaskan
dengan sudut r. Cepat
rambat
cahaya
di
medium 1 adalah v1 dan
di medium 2 adalah v2.
Waktu yang diperlukan
cahaya untuk merambat
dari
B
dengan
ke
D
sama
waktu
yang
dibutuhkan dari A ke E
sehingga DE menjadi
muka gelombang pada
medium 2.
Gambar 18. Muka gelombang pada pembiasan cahaya dari medium1 ke medium 2.
Pada segitiga ABD berlaku persamaan trigonometri sebagai berikut
284
.
Sin i =
BD v1.t

,
AD AD
sedangkan pada segitiga AED berlaku persamaan trigonometri
sebagai berikut, Sin r =
AE v 2 .t

. Bila kedua persamaan dibandingkan akan diperoleh
AD AD
sin i v1

sin r v 2
Pada peristiwa pembelokan cahaya dari medium 1 ke medium 2 ini besaran frekuensi
cahaya tetap atau tidak mengalami perubahan. Karena v = .f maka berlaku pula,
sin i 1

sin r 2
Sehingga berlaku persamaan pembiasan
sin i n 2 v1 1



sin r n1 v 2 2
Dengan keterangan,
n1
: indeks bias medium 1
n2
: indeks bias medium 2
v1
: cepat rambat cahaya di medium 1
v2
: cepat rambat cahaya di medium 2
λ1
: panjang gelombang cahaya di medium 1
λ2
: panjang gelombang cahaya di medium 2
Di samping menunjukkan perbandingan cepat rambat cahaya di dalam
suatu medium, indeks bias juga menunjukkan kerapatan optik suatu medium. Semakin
besar indeks bias suatu medium berarti semakin besar kerapatan optik medium tersebut.
Bila cahaya merambat dari medium kurang rapat ke medium yang lebih rapat, cahaya
akan dibiaskan mendekati garis normal, sebaliknya bila cahaya merambat dari medium
lebih rapat ke medium kurang rapat akan dibiaskan menjauhi garis normal.
285
.
Gambar 19. sinar merambat dari
medium kurang rapat ke medium lebih
rapat akan dibiaskan mendekati garis
normal, sudut r < i
Contoh Soal:
1. Cepat rambat cahaya di medium A besarnya 2 x 108 m/s. Bila cepat rambat cahaya di
ruang hampa 3 x 108 m/s, berapakah indeks bias mutlak medium itu?
Penyelesaian:
Diketahui :
n1 = 1
v1 = 3 x 108 m/s
v2 = 2 x 108 m/s
Ditanya : n2 = ?
Jawab :
n 2 v1

n1 v 2
n2 = 1,5
2. Seberkas cahaya datang dari udara (nu = 1) ke dalam air (na = 1,33) dengan sudut
datang 30°. Tentukan besar sudut bias!
Penyelesaian
Diketahui :
nu = 1
na = 1,33
286
.
i = 30°
Ditanya : r = ?
Jawab : Berkas sinar berasal dari udara menuju air, berarti n1 = nu = 1 dan n2 = na =1,33.
sin i n 2

sin r n 1
sin 30 0 1,33

sin r
1
0,5
 1,33
sin r
sin r =
0,5
1,33
r = 22,1°
3. Cepat rambat cahaya di dalam kaca 2,00 x 108 m/s dan cepat rambat cahaya di dalam
air 2,25 x 108 m/s.
Tentukan:
a) indeks bias relatif air terhadap kaca
b) indeks bias relatif kaca terhadap air
Penyelesaian:
vkaca = 2,00 x 108 m/s
Diketahui :
vair = 2,25 x 108 m/s
Ditanya :
a) nair-kaca .....?
b) nkaca-air ....?
Jawab :
a) nair-kaca
=
v kaca
v air
=
2.00 x10 8
2,25 x10 8
287
.
= 0,89
4. Berkas sinar merambat di udara dengan kecepatan 3 x 108 m/s dan frekuensi 4,62 x
.
1014 Hz menuju permukaan air yang indeks biasnya
4
. Tentukan panjang gelombang
3
cahaya:
a) saat berada di udara
b) saat berada di air!
Penyelesaian:
Diketahui : c = 3 x 108 m/s
f = 6 x 1014 Hz
nu = n1 = 1
na = n2 =
Ditanya :
4
3
a) λu = ?
b) λa = ?
Jawab : a) c = λ.f
λu = 6,5 x10-7 m
Jadi, panjang gelombang cahaya di udara adalah λ1 = 6,5 x 10-7 m.
b) Panjang gelombang cahaya di dalam air (λ2) bila panjang gelombang cahaya
λ1 = 6,5 x 10-7 m
λ2 = 4,86 x 10-7 m.
288
.
Pemantulan Total
Pada saat cahaya merambat dari medium optik lebih rapat ke medium
optik kurang rapat dengan sudut datang tertentu, cahaya akan dibiaskan menjauhi garis
normal. Artinya sudut bias akan selalu lebih besar dibandingkan sudut datang. Apabila
sudut datang cukup besar, maka sudut bias akan lebih besar lagi, Apa yang terjadi, bila
sudut datang terus diperbesar?
Bila sudut datang terus diperbesar, maka suatu saat sinar bias akan sejajar dengan bidang
yang berarti besar sudut biasnya (r) 90°. Tidak ada lagi cahaya yang dibiaskan,
seluruhnya akan dipantulkan. Sudut datang pada saat sudut biasnya mencapai 90° ini
disebut sudut kritis atau sudut batas. Pemantulan yang terjadi disebut pemantulan total
atau pemantulan sempurna. Persamaan sudut kritis sebagai berikut.
sin i n 2

sin r n 1
sin i k
n
 2
0
n1
sin 90
sin ik =
n2
n1
Keterangan
ik = sudut kritis medium lebih rapat (asal sinar datang)
n1 = indeks bias medium kurang rapat (tempat sinar bias)
n2 = indeks bias bahan lebih rapat (asal sinar datang)
n1> n2
Contoh:
Berkas sinar datang dari intan ke udara. Bila indeks bias intan = 2,4 dan indeks bias
udara = 1 tentukan sudut kritis pada intan!
289
.
Penyelesaian:
Diketahui : n1 = 2,4
n2 = 1
Ditanya : ik = ?
Jawab :
sin ik =
n2
n1
sin ik =
1
= 0,417
2,4
ik = 24,6°
Jadi, sudut kritis untuk intan adalah 24,6°. Artinya bila sinar datang dari intan menuju
udara dengan sudut datang lebih besar dari 24,6°, maka sinar-sinar tersebut akan
dipantulkan kembali ke intan. Oleh karena itu, intan dibentuk sedemikian sehingga
hampir semua sinar datang ke permukaannya membentuk sudut yang lebih besar dari
24,6° sehingga sinar yang datang ke intan setelah masuk ke permukaan dalamnya akan
dipantulkan sempurna. Akibatnya intan tampak berkilauan.
Gambar 20. Intan berkilauan akibat pemantulan sempurna.
290
.
Pemantulan total diterapkan pada banyak alat optik antara lain periskop, teleskop,
mikroskop, dan teropong binokuler. Dewasa ini dikembangkan pemakaian serat optik.
Serat optik adalah pipa kecil dan panjang terbuat dari plastik atau kaca yang digunakan
untuk penyalur cahaya. Serat optik terdiri dari inti serat yang terbuat dari kaca berkualitas
dan berindeks bias tinggi yang dibungkus oleh lapisan tipis kaca yang indeks biasnya
lebih rendah serta bagian luar serat yang terbuat dari plastik atau bahan lain untuk
melindungi inti serat. Cahaya dapat melewati serat optik dari ujung yang satu ke ujung
yang lain meskipun serat optik itu dibengkokkan. Endoskop dibuat dengan
memanfaatkan serat optik. Dengan bantuan endoskop para dokter dapat melihat bagian
dalam tubuh manusia (misalnya lambung) dan bahkan memotretnya. Dalam teknologi
komunikasi serat optik digunakan untuk mengirim sinyal-sinyal komunikasi.
Gambar 21. Alat kedokteran
endoskop dibuat dari serat optic
yang mempunyai kemampuan
untuk pemantulan sempurna di
dalamnya, sehingga dokter dapat
melihat bagian dalam tubuh,
saluran pencernaan misalnya.
Latihan
Kerjakan di buku tugasmu!
1). Seberkas cahaya terang dari udara memasuki air dengan indeks bias air 4/3.
Apabila sudut datang cahaya 300. Tentukan:
a) Cepat rambat cahaya di air
b) Sudut bias cahaya
c) Lukis pembiasan sinar
2). Sinar datang dari kaca ke air dengan sudut datang 450. Indeks bias kaca dan
indeks bias air berturut-turut 3/2 dan 4/3. jika panjang gelombang sinar dalam
kaca adalah 4000 Å, tentukan : (1 Å = 10-10 m)
291
.
a) Sudut bias
b) Panjang gelombang dalam air
c) Kecepatan sinar dalam kaca, apabila kecepatan sinar di air 2.108m/s.
d) Frekuensi sinar
3). Seberkas sinar datang dari udara ke lapisan minyak yang terapung di air dengan
sudut datang 30°. Bila indeks bias minyak 1,45 dan indeks bias air 1,33,
berapakah besar sudut sinar tersebut di dalam air?
b. Pembiasan Cahaya Pada Plan Paralel (Balok Kaca)
Kaca plan paralel atau balok kaca adalah keping kaca tiga dimensi yang dibatasi oleh sisisisi yang sejajar.
Gambar 22. Sebuah kaca
plan paralel atau balok
kaca. Dibatasi oleh tiga
pasang sisi – sisi sejajar
Cahaya dari udara memasuki sisi pembias kaca plan paralel akan dibiaskan mendekati
garis normal. Demikian pula pada saat cahaya meninggalkan sisi pembias lainnya ke
udara akan dibiaskan menjauhi garis normal. Pengamat dari sisi pembias yang
berseberangan akan melihat sinar dari benda bergeser akibat pembiasan. Sinar bias akhir
mengalami pergeseran sinar terhadap arah semula.
292
.
Gambar 23. Pergeseran sinar bias
terhadap arah semula dari sinar datang
pada kaca plan paralel. Berkas sinar bias
akhir sejajar dengan sinar datang namun
bergeser sejauh jarak titik G-C
Menentukan besar pergeseran sinar.
i1
A

d
s
B
D
t
C
r2
Pada segitiga ABC siku-siku di B:
d
cos r1 
maka
s
Tinjau arah sinar di dalam kaca plan paralel.
s
d
cos r1
Pada segitiga ACD siku-siku di D:
t
sin  
maka t  s. sin 
s
Pergeseran sinarnya sejauh t,
maka:
t
d
.sin α.
cosr1
293
.
i1  α  r1
Karena
α  i1  r1
maka
Ketentuan lain adalah berlaku:
d.sin(i 1  r1 )
cosr1
t
i1 = r2
r1 = i2
dengan keterangan
d = tebal balok kaca, (cm)
i = sudut datang, (°)
r = sudut bias, (°)
t = pergeseran cahaya, (cm)
Contoh soal:
Seberkas sinar memasuki balok kaca dari udara (nu = 1) dengan sudut datang i = 30°.
Bila indeks bias balok kaca 1,52 dan ketebalannya 4 cm tentukan jarak pergeseran
sinar setelah sinar yang masuk itu keluar dari balok kaca!
Penyelesaian:
Diketahui :
i = 30º
n1 = nu = 1
n2 = nk = 1,52
d = 4 cm
Ditanya : t = ?
Jawab:
n1 sin i = n2 sin r
sin r =
n1
n2
=
sin r
sin i
1
1
.sin 30° =
. 0,5
1,52
1,52
= 0,33
294
.
r = 19,2°
t
d . sin( i1  r1 )
cos r1
0
,2 0 )
t = 4 x sin( 30  19
= 0,79 cm.
0
cos19,2
Tugas
Kerjakan di buku tugasmu!
1. Seberkas sinar datang dari udara (nudara = 1) menuju balok kaca yang indeks biasnya
1,41 dengan sudut datang 45°. Jika tebal balok kaca 1,41 cm, tentukan besar
pergeseran sinar yang datang ke balok kaca dan sinar yang keluar dari balok kaca!
2. Seberkas cahaya datang dengan sudut 40° dari udara (nudara = 1) ke balok kaca (nkaca =
1,5) yang tebalnya 8 cm. Berapakah pergeseran berkas sinar tersebut setelah keluar
dari balok kaca?
c. Pembiasan Cahaya Pada Prisma Kaca
Prisma juga merupakan benda bening yang terbuat dari kaca, kegunaannya
antara lain untuk mengarahkan berkas sinar, mengubah dan membalik letak bayangan
serta menguraikan cahaya putih menjadi warna spektrum (warna pelangi).
Cahaya dari udara memasuki salah satu bidang pembias prisma akan dibiaskan dan pada
saat meninggalkan bidang pembias lainnya ke udara juga dibiaskan.
Gambar 24. Sebuah prisma kaca
dibatasi oleh dua segitiga dan tiga
segiempat
295
.
Rumus sudut puncak/pembias :
β  r1  i 2
Sedangkan rumus sudut deviasi :
δ  i1  r2  β
pada bidang pembias I :
sini 1 n k

sinr 1 n ud
pada bidang pembias II :
sini 1 n ud

sinr 2 n k
Sudut deviasi adalah sudut yang dibentuk oleh perpanjangan sinar datang dan sinar bias
prisma.
Pada saat i1 = r2 dan r1 = i2, sudut deviasi menjadi sekecil-kecilnya disebut sudut Deviasi
Minimum (  m).
Menentukan persamaan sudut deviasi minimum.
Karena i1 = r2
δ  i1  r2  β
δm  i1  i1  β
δm  β  2i1
i1 
dan r1 = i2
δm  β
2
β  r1  i 2
β  r1  r1
β  2r1  r1 
sehingga :
β
2
sini 1 n 2

sinr 1 n 1
δm  β
)
n
2
 2
β
n1
sin( )
2
sin(
untuk prisma dengan sudut pembias  ≤ 150, sudut deviasi minimum ditentukan
tersendiri. Karena sudut deviasi menjadi sangat kecil (δm) sehingga nilai sin α = α.
Akibatnya persamaan Hukum Snellius di atas berubah dari,
296
.
δm  β
)
n
2
 2
β
n1
sin( )
2
sin(
(
δm  β
)
n
2
 2
β
n1
( )
2
δm  β n 2

β
n1
δm 
n2
β β
n1
δm  (
n2
 1)β
n1
Contoh :
1. Sebuah prisma dengan sudut pembias 600 mempunyai indeks bias 1,67. Hitung
a. Sudut deviasinya jika sudut datangnya 600.
b. Sudut deviasi minimum
c. Sudut deviasi minimum jika sudut pembias prisma 100.
Penyelesaian
β = 60o
a)  = …. ? i1 = 60o
n2 = 1,67
b) m = …. ?
n1 = 1
c) m = …. ? β = 10o
Jawab :
a)  = i1 + r2 – β
= 60o + 53,28 – 60o
 = 53,28o
sin i 1
sin r1
=
n prisma
n uara
β = i2 + r1
60o = i2 + 31,23o
i2
= 60o – 31,23o
i2
= 28,77o
sin i 2
sin r2
297
=
n prisma
n uara
.
1,67
sin 60 o
=
1
sin r1
sin 28,77
1
=
sin r2
1,67
0,866
sin r1
= 1,67
0,48
sin r2
=
sin r1
=
0,866
1,67
sin r2
= 0,48 . 1,67
sin r2
= 0,8016
sin r1
= 0,518
r2
= 53,28o
= 31,23o
r1
   
sin  m

 2 
b)

sin  
2
   
sin  m

 2 
=
=
n prisma
n uara
n prisma
n uara

. sin  
2
  m  60 o
sin 
2


1,67
 =
. sin

2

  m  60 o
sin 
2


 = 1,67 . sin 30o


  m  60 o
sin 
2


 = 1,67 . 0,5


  m  60 o
sin 
2


 = 0,835


 m  60 o
2
 60 o

 2



= 56,615o
m + 60o = 2 . 56,615o
m = 113,23o – 60o
m = 53,23o
c) β = 10o
n

→ m =  2  1 β
 n1

298
1
1,67
.
 n prisma

m = 
1 β
 n udara

 1,67

 1 10o = 0,67 . 10 = 6,7o
m = 
 1

2. Sebuah prisma (np = 1,50) mempunyai sudut pembias β = 10°. Tentukan deviasi
minimum pada prisma tersebut!
Penyelesaian:
Karena sudut pembiasnya β < 15° gunakan persamaan deviasi minimum
m = (n21– 1). β
Diketahui :
n1 = nu = 1
n2 = np = 1,50
β = 10°
Ditanya : m = ?
Jawab :
m = (n21– 1) β
n

=  2  1 β
 n1

= (1,5 – 1) 10°
m = 5°.
Tugas
Kerjakan di buku tugasmu!
1. Sudut pembias sebuah prisma yang indeks biasnya 1,56 adalah 30°. Jika sinar datang
ke salah satu bidang batas antara udara dan prisma dengan sudut 30°, tentukanlah:
a) sudut deviasi prisma; dan
b) sudut deviasi minimum prisma!
2. Hitung sudut datang yang menghasilkan deviasi minimum pada sebuah prisma yang
sudut pembiasnya adalah 45° bila indeks biasnya = 1,5 dan indeks bias udara = 1
299
.
3. Berapakah besar sudut deviasi minimum sebuah prisma (nprisma = 1,5) di udara jika
sudut pembiasnya 12°?
d. Pembiasan Cahaya Pada Permukaan Lengkung
Permukaan lengkung lebih dikenal sebagai Lensa tebal, dalam kehidupan sehari-hari
dapat diambilkan contoh, antara lain :
-
Akuarium berbentuk bola
-
Silinder kaca
-
Tabung Elenmeyer
-
Plastik berisi air di warung makan
Gambar 25. Permukaan lengkung atau lensa tebal
Sinar-sinar dari benda benda yang berada pada medium 1 dengan indeks bias mutlak n1 di
depan sebuah permukaan lengkung bening yang indeks bias mutlaknya akan dibiaskan
sehingga terbentuk bayangan benda. Bayangan ini bersifat nyata karena dapat ditangkap
layar.
Persamaan yang menyatakan hubungan antara indeks bias medium, indeks bias
permukaan lengkung, jarak benda, jarak bayangan, dan jari-jari permukaan lengkung
dapat dirumuskan sebagai berikut.
 n1 n 2   n 2  n1 
 s  s'    R 

 

(Coba buktikanlah persamaan tersebut!)
300
.
Dengan keterangan,
n1 = indeks bias medium di sekitar permukaan lengkung
n2 = indeks bias permukaan lengkung
s = jarak benda
s' = jarak bayangan
R = jari-jari kelengkungan permukaan lengkung
Syarat : R = (+) jika sinar datang menjumpai permukaan cembung
R = (-) jika sinar datang menjumpai permukaan cekung
Seperti pada pemantulan cahaya, pada pembiasan cahaya juga ada perjanjian tanda
berkaitan dengan persamaan-persamaan pada permukaan lengkung seperti dijelaskan
dalam tabel berikut ini.
s+
Jika benda nyata/sejati (di depan permukaan lengkung)
s-
Jika benda maya (di belakang permukaan lengkung)
s'+
Jika bayangan nyata (di belakang permukaan lengkung)
s'-
Jika bayangan maya (di depan permukaan lengkung)
R+
Jika permukaan berbentuk cembung dilihat dari letak benda
R-
Jika permukaan berbentuk cekung dilihat dari letak benda
Pembiasan pada permukaan lengkung tidak harus menghasilkan bayangan yang
ukurannya sama dengan ukuran bendanya.
Pembentukan bayangan pada permukaan lengkung.
301
.
Gambar 26. Pembiasan cahaya pada permukaan lengkung
Sinar dari benda AB dan menuju permukaan lengkung dibiaskan sedemikian oleh
permukaan tersebut sehingga terbentuk bayangan A'B'. Bila tinggi benda AB = h dan
tinggi bayangan A'B' = h', akan diperoleh
tan i =
h
s
atau
h = s tan i
tan r =
h'
s'
atau
h’ = s’ tan r
Perbesaran yang terjadi adalah
dan
M=
h' s' tan r
=
s tan r
h
Bila i dan r merupakan sudut-sudut kecil, maka harga tan i = sin i dan tan r = sin r
s' sin r
s sin i
sehingga
M=
Karena
sin i n 2

sin r n 1
atau
sin r n 1

sin i n 2
maka diperoleh persamaan
perbesaran pada permukaan lengkung sebagai berikut.
M=
s' n 1
s n2
Permukaan lengkung mempunyai dua titik api atau fokus. Fokus pertama (F1) adalah
suatu titik asal sinar yang mengakibatkan sinar-sinar dibiaskan sejajar. Artinya bayangan
akan terbentuk di jauh tak terhingga (s’ = ~) dan jarak benda s sama dengan jarak fokus
n   n  n1 
n
pertama (s = f1) sehingga dari persamaan permukaan lengkung  1  2    2
s'   R 
s
di peroleh
 n1 n 2   n 2  n1 
  
~   R 
 f1
, sehingga
302
 n1
  n 2  n1 
  0  
 atau
f
R


 1

.
1 n 2  n1

f
n 1R
Sehingga jarak fokus pertamanya sebesar, f1 =
n 1R
n 2  n1
Fokus kedua (F2) permukaan lengkung adalah titik pertemuan sinar-sinar bias apa bila
sinar-sinar yang datang pada bidang lengkung adalah sinar-sinar sejajar. Artinya benda
berada jauh di tak terhingga (s = ) sehingga dengan cara yang sama seperti pada
penurunan fokus pertama di atas, kita dapatkan persamaan fokus kedua permukaan
lengkung.
f2 =
n 2R
n 2  n1
Contoh soal:
1. Jari-jari salah satu ujung permukaan sebuah silinder kaca (nkaca = 1,5) setengah bola
adalah 2 cm. Sebuah benda setinggi 2 mm ditempatkan pada sumbu silinder tersebut
pada jarak 8 cm dari permukaan itu. Tentukan jarak dan tinggi bayangan bila silinder
berada:
a) di udara (nudara = 1)
b) di air (nair =
4
)
3
Penyelesaian:
a. Diketahui n1 = nu = 1
n2 = nkaca = 1,5
s = 8 cm
h = 2 mm = 0,2 cm
303
.
R = +2 cm (R bertanda positif karena permukaan
cembung)
Ditanya : s' dan h'
Jawab :
 n1 n 2   n 2  n1 
 s  s'    R 

 

 1 1,5  1,5  1
 8  s'    2 
1,5 1 1
 
s' 4 8
s’ = 1,5 x 8 = 12 cm
M=
s' n 1
s n2
M=
12 x 1
8 x 1,5
M = 1 kali
h'
h
M=
1=
h'
2
h’ = 2 mm
b.Diketahui: n1 = nair =
n2 = nkaca = 1,5
s = 8 cm
304
.
h = 2 mm = 0,2 cm
R = + 2 cm (R bertanda positif karena permukaan
cembung)
Ditanya : s' dan h'
Jawab :
s' = -1,5 x 12 = -18 cm
M=
s' n 1
s n2
M=
- 18 x 4/3
8 x 1,5
M=2
M=
1=
h'
h
h'
2
h’ = 2 mm
2. Sebuah balok gelas (n = 1,5) salah satu ujungnya cekung
dengan jari-jari 18 cm. Sebuah benda tegak berada 24 cm
dari permukaan lengkung itu pada sumbu balok kaca itu.
Tentukan letak dan perbesaran bayangan!
305
.
Penyelesaian:
DDiketahui : n1 = nkaca = 1,5 (benda ada di dalam permukaan lengkung)
n2 = nudara = 1
s = 24 cm
R = 18 cm ( bertanda positif karena permukaan cembung)
Ditanya : s’ dan h’
Jawab :
M=
s' n 1
s n2
M=
- 11,08 x 1,5
1 x 24
M = 0,69
M=
h'
h
0,69 =
h'
1
h’ = 0,69 mm
306
.
3. Seekor ikan berada di dalam akuarium berbentuk bola
dengan jari-jari 30 cm. Posisi ikan itu 20 cm dari dinding
akuarium dan diamati oleh seseorang dari luar akuarium
pada jarak 45 cm dari dinding akuarium. Bila indeks bias air
akuarium
tentukanlah jarak orang terhadap ikan menurut
a) orang itu
b) menurut ikan.
Penyelesaian:
a. Menurut orang (orang melihat ikan), berarti berkas sinar datang dari ikan ke mata
orang)
Diketahui :
n1 = nair =
n2 = nudara = 1
s = 20 cm
R = -30
(R bertanda - karena sinar datang dari ikan menembus permukaan cekung akuarium
ke mata orang)
Ditanya : s’
Jawab :
307
.
s’= -18 cm
Jadi menurut orang, jarak ikan ke dinding akuarium menurut orang hanya 18 cm
(bukan 20 cm!). s’ - menyatakan bayangan ikan maya.
Berarti menurut orang, jarak orang ke ikan adalah 45 cm + 18 cm = 63 cm (bukan 65
cm!).
b. Menurut orang (ikan melihat orang), berkas sinar datang dari orang ke mata ikan
Diketahui :
n1 = nudara = 1
n2 = nair =
s = 45 cm
R = +30
(R bertanda positif karena sinar datang dari orang menembus permukaan cembung
akuarium ke mata ikan)
Ditanya : s’
Jawab :
308
.
= -120 cm
Jadi menurut ikan, jarak orang ke dinding akuarium bukan 45 cm melainkan 120 cm.
Jarak orang ke ikan menurut ikan sama dengan 20 cm + 120 cm = 140 cm. Ikan
merasa orang masih sangat jauh dari jarak yang sebenarnya.
4. Seekor ikan terletak di dalam sebuah akuarium berbentuk bola dengan
diameter 150 cm (nair = 4/3). Ikan berada 50 cm dari dinding akuarium.
Seseorang berdiri pada jarak 100 cm dari dinding akuarium tersebut.
a. Dimana bayangan ikan yang dilihat orang.
b. Dimana bayangan orang yang dilihat ikan.
Penyelesaian
Diketahui:
D = 150 cm maka R = 75 cm
Ditanya :
a. s1 = …. ? orang melihat ikan
b. s1 = …. ? ikan melihat orang
Jawab :
a) Sinar dari air ke udara
n1
= nair
309
.
n2
= nudara
s
= 50 cm
R
= -75 cm ( sinar menjumpai permukaan lengkung)
n1 n 2

S S1
4
3 1
50 S1
4
1
 1
150 S
4
1
 1
150 S
=
n 2  n1
R
1
4
1
=
–
1
225 150
S
1 4
4
24
1
=
–
1
900 150
S
1
 20
1
=
1
900
S
3
=
 75
=
=
3
 75
S1 =
1
225
900
= - 45 cm
 20
b) Sinar dari udara ke air
n1
= nudara
n2
= nair
S
= 100 cm
R
= 75 (sinar menjumpai permukaan cembung)
n1 n 2

S S1
=
n 2  n1
R
4
4
9
=
–
1
900 900
3S
4
1
 31
100 S
=
4 1
3
75
4
5
=
1
900
3S
1
4
 1
100 3S
1
=
225
4
3S1
=
-15S1 = 3600
1
1
–
225 100
3600
 15
S1
=
S1
= –240 cm
( tanda - artinya maya )
310
.
5.
S = 30 cm R = 20 cm
n2 = 1,5
n1 = 1
Permukaan salah satu balok gelas berbentuk setengah bola cekung dengan jari-jari 20
cm. sebuah benda tegak berada 30 cm di depan permukaan lengkung tersebut pada
sebuah balok. Tentukan letak dan perbesaran bayangan (ngelas = 1,5)]
Penyelesaian
Dik : R = – 20 cm
s = 30 cm
n1 = 1
n2
( udara )
= 1,5 ( glass )
Dit : s1= …. ?
M = …. ?
Jawab :
a)
n1 n 2

S S1
=
n 2  n1
R
b) M =
1 1,5
1,5  1
 1 =
30 S
 20
n 1 . S1
n2 .S
 180
7
M=
1,5  30
1
1 1,5
0,5
 1 = 
30 S
20
1
1
34

=
40 30
120
M=
12
kali
21
120  1.5
180
= 
cm
7
7
M=
4
X
7
1,5
S1
=
S1
=
311
.
= – 25,71 cm
( tanda - artinya maya )
Latihan
1. Sebuah akuarium berbentuk bola dengan jari-jari 60 cm berisi air yang
indeks biasnya . Seekor ikan di dalam akuarium itu berada pada jarak 40
cm dari dinding akuarium dan diamati oleh orang di luar akuarium 90 cm
dari dinding akuarium tersebut. Tentukanlah jarak orang ke ikan:
a) menurut orang
b) menurut ikan
2. Tentukan jarak fokus suatu permukaan lengkung dari kaca (nkaca = 1,5)
yang berjari-jari 15 cm di udara.
3. Seekor ikan terletak di dalam akuarium berbentuk bola dengan jari-jari 50
cm. Seorang pengamat melihat ikan yang berada 20 cm dari permukaan
dinding akuarium di luar akuarium itu. Jika indeks bias air akuarium 4/3,
tentukan bayangan ikan dilihat oleh:
a. pengamat yang berdiri pada jarak 1 m dari dinding akuarium itu!
b. oleh ikan!
e. Pembiasan Cahaya Pada Lensa Tipis
Lensa adalah benda bening yang dibatasi oleh dua permukaan dan minimal salah satu
permukaannya itu merupakan bidang lengkung. Lensa tidak harus terbuat dari kaca yang
penting ia merupakan benda bening (tembus cahaya) sehingga memungkinkan terjadinya
pembiasan cahaya. Oleh karena lensa tipis merupakan bidang lengkung. Ada dua macam
kelompok lensa :
a. Lensa Cembung (lensa positif/lensa konvergen)
312
.
Yaitu lensa yang mengumpulkan sinar.
Gambar 27. Lensa cembung bersifat
mengumpulkan sinar di satu bidang fokus
Lensa cembung dibagi lagi menjadi tiga:
1. lensa cembung dua (bikonveks)
2. lensa cembung datar (plan konveks)
3. lensa cembung cekung (konkaf konveks)
Gambar 28.Macam-macam lensa cembung
b. Lensa Cekung (lensa negatif/lensa devergen)
Yaitu lensa yang menyebarkan sinar .
Gambar 29. Lensa cekung bersifat
menyebarkan sinar dari arah bidang fokus
Lensa cekung dibagi lagi menjadi tiga:
313
.
1. lensa cekung dua (bikonkaf)
2. lensa cekung datar (plan konkaf)
3. lensa cekung cekung (koveks konkaf)
Gambar 30. Macam-macam lensa cekung
Untuk memudahkan pembuatan diagram lensa digambar dengan garis lurus dan tanda di
atasnya, untuk lensa cembung di tulis (+) dan lensa cekung (–). Untuk lensa memiliki dua
titik fokus.
1. Berkas Sinar Istimewa pada Lensa Tipis
Seperti pada cermin lengkung, pada lensa dikenal pula berkas-berkas sinar istimewa.
a. Berkas sinar-sinar istimewa pada lensa cembung.
Ada tiga macam sinar istimewa pada lensa cembung.
314
.
Gambar 31 .Sinar-sinar istimewa pada lensa cembung
(1). Sinar datang sejajar sumbu utama lensa, dibiaskan melalui titik fokus.
(2). Sinar datang melalui titik fokus lensa, dibiaskan sejajar sumbu utama.
(3). Sinar datang melalui titik pusat lensa tidak dibiaskan melainkan diteruskan.
b. Berkas sinar-sinar istimewa pada lensa cekung.
Ada tiga macam sinar istimewa pada lensa cekung.
Gambar 32 .Sinar-sinar istimewa pada lensa cekung
(1). Sinar datang sejajar sumbu utama dibiaskan seolah-olah berasal dari titik fokus.
(2). Sinar datang seolah-olah menuju titik fokus lensa dibiaskan sejajar sumbu utama.
(3). Sinar datang melalui titik pusat lensa tidak dibiaskan melainkan diteruskan.
2. Penomoran ruang pada Lensa Tipis
Untuk lensa nomor ruang untuk benda dan nomor-ruang untuk bayangan dibedakan.
nomor ruang untuk benda menggunakan angka Romawi (I, II, III, dan IV), sedangkan
untuk ruang bayangan menggunakan angka Arab (1, 2, 3 dan 4) seperti pada gambar
berikut ini:
315
.
Untuk ruang benda berlaku :
ruang I antara titik pusat optic (O) dan F2,
ruang II antara F2 dan 2F2
ruang III di sebelah kiri 2F2,
ruang IV benda (untuk benda maya) ada di belakang lensa.
Untuk ruang bayangan berlaku :
ruang 1 antara titik pusat optic (O) dan F1,
ruang 2 antara F1 dan 2F1
ruang 3 di sebelah kanan 2F1,
ruang 4 (untuk bayangan maya) ada di depan lensa.
Berlaku pula : R benda + R bayangan = 5
3. Melukis pembentukan bayangan pada lensa
Untuk melukis pembentukan bayangan pada lensa tipis cukup menggunakan minimal dua
berkas sinar istimewa untuk mendapatkan titik bayangan.
Contoh melukis pembentukan bayangan.

Benda AB berada di ruang II lensa cembung
Sifat-sifat bayangan yang
terbentuk:
Nyata, terbalik, diperbesar

Benda AB berada di ruang III lensa cembung
316
.
Sifat-sifat bayangan yang
terbentuk:
Nyata, terbalik, diperkecil

Benda AB berada di ruang I lensa cembung
Sifat-sifat bayangan yang
terbentuk:
maya, tegak, diperbesar

Benda AB berada di ruang II lensa cekung
Sifat-sifat bayangan yang
terbentuk:
Maya, tegak, diperkecil
Latihan
Lukislah bayangan benda AB di buku tugasmu bila posisinya:
a. tepat di titik fokus F2 lensa cembung
b. tepat di titik 2 F2 lensa positif.
317
.
c. dari jauh tak terhingga
d. di ruang III lensa cekung
4. Rumus-rumus Pada Lensa Tipis
Untuk lensa tipis yang permukaannya sferis (merupakan permukaan bola), hubungan
antara jarak benda (s), jarak bayangan (s') dan jarak fokus (f) serta perbesaran bayangan
benda (M) diturunkan dengan bantuan geometri dapat dijelaskan berikut ini.
Gambar 33. Lensa sferis,
permukaannya
merupakan permukaan
bola.
Dari persamaan lensa lengkung,
 n1 n 2   n 2  n1 
 s  s'    R 

 

Berkas sinar yang berasal dari O ketika melewati permukaan ABC dibiaskan sedemikian
sehingga terbentuk bayangan di titik I1. Oleh permukaan ADC bayangan I1 itu di anggap
benda dan dibiaskan oleh permukaan ADC sedemikian sehingga terbentuk bayangan
akhir di titik I2
Pada permukaan lengkung ABC , sinar dari benda O dari medium n1 ke lensa n2,
sehingga s = OB, s’ = BI1
maka
 n1
n   n  n1 
 2  2


 OB BI 1   R 1 
Pada permukaan lengkung ADC , sinar dari lensa ke medium n1, s = -DI1, s’ = DI2
maka
 n2
n  n  n2 
 1  1


 - DI 1 DI 2   - R 2 
318
.
Karena dianggap lensa tipis maka ketebalan BD diabaikan, sehingga BI1 = DI1 dan saling
meniadakan karena berlawanan tanda . Apabila kedua persamaan dijumlahkan diperoleh :
 n1
n   n  n1   n 1  n 2 
 1  2

+

OB
DI
R
2
2


   R1 
 n1 n1   n 2  n1   n1  n 2 
 s  s'    R  +   R 

 
2
1 
 
 n1 n1   n 2  n1   n 2  n1 
 s  s'    R  +  R 

 
2
1
 

1 
 n 1 n 1   n 2  n 1  1



    
s'   R 2  R 1 R 2 
 s
Semua ruas dibagi dengan n1 akan diperoleh persamaan lensa tipis sebagai berikut.
 1
1 
1 1   n2

 1

    
R
R
 s s'   n 1
2 
 1
Dengan keterangan,
s = jarak benda
s' = jarak bayangan
n1 = indeks bias medium sekeliling lensa
n2 = indeks bias lensa
R1 = jari-jari kelengkungan permukaan pertama lensa
R2 = jari-jari kelengkungan permukaan kedua lensa
Persamaan lensa tipis tersebut berlaku hanya untuk sinar-sinar datang
yang dekat dengan sumbu utama lensa (sinar-sinar paraksial) dengan ketebalan lensa jauh
lebih kecil dibandingkan dengan jari-jari kelengkungannya.
Jarak fokus lensa (f) adalah jarak dari pusat optik ke titik fokus (F). Jadi
bila s = ~ bayangan akan terbentuk di titik fokus (F), maka s’= f.
 1
1 
1 1   n2

 1

    
 s s'   n 1
 R 1 R 2 
 1
1 
 1 1   n2

 1

    
 ~ f   n1
 R 1 R 2 
319
.
Karena
1
1  n 2  1
1 

= 0 maka rumus jarak fokus lensa :
 
 1

~
f  n1
 R 1 R 2 
 1
1 
1 1   n
 disubstitusikan dengan persamaan
Bila persamaan      2  1

 s s'   n 1
 R 1 R 2 
1  n 2  1
1 
 maka akan didapat persamaan baru yang dikenal sebagai
 
 1

f  n1
R
R
2 
 1
persamaan pembuat lensa, yaitu
1 1 1
 
f s s1
Dengan keterangan,
n1 = indeks bias medium sekeliling lensa
n2 = indeks bias lensa
R1 = jari-jari kelengkungan permukaan pertama lensa
R2 = jari-jari kelengkungan permukaan kedua lensa
R = bertanda (+) jika permukaan lensa yang dijumpai berbentuk cembung
R = bertanda (-) jika permukaan lensa yang dijumpai berbentuk cekung
R=
 jika permukaan lensa yang dijumpai berbentuk datar
s = jarak benda bertanda positif (+) jika benda terletak di depan lensa (benda nyata).
s = jarak benda bertanda negatif (–) jika benda terletak di belakang lensa (benda maya).
s’ = jarak bayangan bertanda positif (+) jika bayangan terletak di belakang lensa
(bayangan nyata).
s’ = karak bayangan bertanda negatif (–) jika benda terletak di depan lensa (bayangan
maya).
f = jarak fokus bertanda positif (+) untuk permukaan lensa positif (lensa cembung).
f = jarak fokus bertanda negatif (–) untuk permukaan lensa negatif (lensa cekung).
5. Perbesaran bayangan
Untuk menentukan perbesaran bayangan lensa tipis dapat menggunakan persamaan
sebagai berikut.
320
.
M
s1
h'

s
h
Dengan keterangan,
s = jarak benda
s' = jarak bayangan
h = tinggi benda
h' = tinggi bayangan
M > 1 = bayangan diperbesar
M < 1 = bayangan diperkecil
s1 (+) = bayangan nyata
s1 () = bayangan maya
6. Daya / Kekuatan Lensa
Daya Lensa adalah kekuatan lensa dalam memfokuskan lensa. Daya lensa berkaitan
dengan sifat konvergen (mengumpulkan berkas sinar) dan divergen (menyebarkan sinar)
suatu lensa. Untuk Lensa positif, semakin kecil jarak fokus, semakin kuat kemampuan
lensa itu untuk mengumpulkan berkas sinar. Untuk lensa negatif, semakin kecil jarak
fokus semakin kuat kemampuan lensa itu untuk menyebarkan berkas sinar. Oleh karena
itu
kuat
lensa
didefinisikan
sebagai
kebalikan
dari
jarak
fokus,
Rumus kekuatan lensa (power lens)
P=
1
1
dengan satuan
= Dioptri
f
meter
Untuk menambah kekuatan lensa kita dapat gunakan lensa gabungan dengan sumbu
utama dan bidang batas kedua lensa saling berhimpit satu sama lain. Dari penggabungan
lensa ini maka akan didapatkan fokus gabungan atau daya lensa gabungan.
321
.
Gambar 34. Diagram lensa
gabungan
Suatu lensa gabungan merupakan gabungan dari dua atau lebih lensa dengan sumbu
utamanya berhimpit dan disusun berdekatan satu sama lain sehingga tidak ada jarak
antara lensa yang satu dengan lensa yang lain (d = 0).
Persamaan lensa gabungan dirumuskan sebagai berikut.
1
f gab

1 1 1
   ....
f1 f 2 f 3
dan daya lensa sebagai berikut.
Pgab  P1  P2  P3  ....
Berlaku ketentuan untuk lensa positif (lensa cembung), jarak fokus (f) bertanda plus,
sedangkan untuk lensa negatif (lensa cekung), jarak fokus bertanda minus.
Contoh Soal:
1. Antara dua lensa positif yang jarak fokusnya 6 cm dan 10 cm disisipkan sebuah
lensa negatif dengan fokus 8 cm. Tentukan jarak fokus lensa gabungan dan kuat
lensa gabungan tersebut!
Penyelesaian:
Diketahui : f1 = +6 cm
f2 = -8 cm
322
.
f3 = +10 cm
Ditanya :
fgab dan Pgab = ?
Jawab:
fgab =
120
= 7,06 cm
17
Daya / kuat lensa gabungan :
P=
1
f gab
=
1
7,06 cm
=
100
7,06 m
P = 14,17 dioptri.
2. Sebuah lensa bikonveks mempunyai jari-jari kelengkungan 80 cm dan 40 cm
terbuat dari gelas (n = 1,56). Hitung jarak fokus dan kuat lensa.
323
.
Penyelesaian
Diket : Bikonveks
n2
n1
R1
R2
n1
R1 = 80 cm n2 = 1,56
R2 = 40 cm n1 = 1
Dit : f = …. ?
P = …. ?
Jawab :
 1
1  n2
1 

= 
 1 

f
 n1
  R1 R 2 
P=
atau
1  1,56   1
1 
 1   
=
f
 1
  80 40 
1
 3  1,68
= 0,56   =
f
80
 80 
f =
1
f meter
80
= 47,62 cm
1,68
P=
100
f ( cm )
P=
100
100
=
= 2,09 dioptri
f
47,62
3. Sebuah lensa cembung mempunyai jari-jari cembungnya 12 cm dan 36 cm.
sebuah benda diletakkan pada jarak 15 cm dari lensa dan bayangannya nyata pada
jarak 72 cm dari lensa. Hitunglah indeks bias lensa.
Penyelesaian
Diket :
R1
= 12 cm
R2 = 36 cm
S1
= 72 cm ( nyata )
n1 = 1
Jawab :
324
S
= 15 cm
.
n
 1
1 

=  2 1 

 n1
  R1 R 2 
1
1
1
= + 1
f
S S
1
f
1
1
1
=
+
f
15 72
29
1 
n
1
=  2 1   
360
 1
  12 36 
1
24
5
=
+
f
360 360
29
1 
 3
= n 2  1   
360
 36 36 
1
29
=
f
360
4
29
= n 2  1 .
36
360
1
360
=
= 12,41 cm
f
29
1
29
= n 2  1 .
9
360
n2 – 1 =
29 9
.
360 1
n2 – 1 =
29
40
n2
29
69
+1=
= 1,725
40
40
=
4. Jarak fokus lensa gelas ( n = 1,5 ) di dalam alkohol ( n = 1,35) adalah 45 cm.
Hitung jarak fokus dan kuat lensa tersebut di udara.
Penyelesaian
Diket :
Dit :
nalk
= 1,35
ng
= 1,5
nud
=1
f
= …. ?
P
= …. ?
f
= 45 cm ( Alkohol )
di udara
Jawab : di alkohol
1
f
n
 1
1 

=  2 1 

 n1
  R1 R 2 
alkohol
g
325
.
1
45
 ng
 1
1 

= 

1 
 n alk
  R1 R 2 
1
45
1 
 1,5
 1

=
1 

 1,35   R 1 R 2 
1
45
1 
 150 135   1


=

 
 135 135   R 1 R 2 
1
45
=
15  1
1 

. 

135  R 1 R 2 
1
45
=
1  1
1 

. 

9  R 1 R 2 
 1
9 1
1  1

 =
.
=

 R 1 R 2  45 1 5
di udara
udara
5. Sebuah
lensa
1
f
n
 1
1 

=  2 1 

 n1
  R1 R 2 
1
f
 ng
 1
= 
1 .
 n ud
 5
1
f
 1,5  1
1 .
=
 1
 5
1
f
=
1 1
.
2 5
1
f
=
1
10
f
= 10 cm = 0,1 m
P=
1
1
=
= 10 dioptri
f 0,1
plankonkaf
mempunyai
panjang
fokus
–25cm.
kelengkungan salah satu permukaannya 12 cm. Hitung indeks bias lensa.
326
Jari-jari
.
Penyelesaian
Diket : Plan Konkaf
f
= - 25 cm
R1 = ~
R2 = - 12 cm ( berbentuk cekung )
R1
R2
n1 = 1
udara
Dit : n2 = …. ?
Jawab :
1
f
n
 1
1 

=  2 1 

 n1
  R1 R 2 
1
 25
1 
n
 1
=  2 1  

 1
   - 12 
1
 25
1

= n 2  1  0  
12 

1
 25
 1
= n 2  1 .   
 12 
n2 – 1
=
1
 12
.
 25
1
n2
=
12
+1
25
n2
=
12
25
37
+
=
= 1,48
25
25
25
6. Sebuah lensa konkaf konveks mempunyai jari-jari kelengkungan 10 cm dan 12
cm terbuat dari kaca dengan indeks bias 1,6. Tentukan:
a. fokus lensa
b. kuat lensa
c. perbesaran bayangan jika sebuah benda diletakkan pada jarak 50 cm.
Penyelesaian
Diket : konkaf konveks
327
.
R1 = -10 cm
R1
R2
R2 = -12 cm
n1 = 1
n2 = 1,6
= …. ?
Dit : a. f
b. P = …. ?
c. M = …. ?
s = 50 cm
Jawab :
a)
n
 1
1 

=  2 1 

n
R
R
2 
 1
 1
1
f
1
 1,6   1
1 . 
 
=
 1
   10 12 
=
6  6
5 
 
. 
10  60 60 
=
6  1 
.  
10  60 
1
 1 
= 

f
 100 
f
= -100 cm = -1 m
b) P =
1
c)
f

1 1
=
= -1 dioptri
f -1
S1
M=
S
1 1
= + 1
S S
1
1
1
=
+ 1
100 50
S
1
S1
=
1
1
–
100 50
1
S1
=
1
2
–
100 100
328
M=
- 100 3
50
M=
2
X
3
.
1
S1
=
3
100
S1
=
100
cm
3
7. Sebuah lensa bikonveks mempunyai jari-jari kelengkungan 9 cm dan 18 cm. Pada
jarak 24 cm ternyata bayangan yang terbentuk nyata pada jarak 24 cm dari lensa.
Hitung :
a. Jarak fokus
b. Kekuatan lensa
c. Indeks bias lensa
Penyelesaian
Dik : Lensa bikonveks
R1 = 9 cm
R1
n2
R2
R2 = 18 cm
S = 24 cm
S1 = 24 cm ( nyata )
= …. ?
Dit : a. f
b. P = …. ?
c. n2 = …. ?
Jawab :
a).
1
f
=
1 1
+
S S1
=
1
1
+
24 24
P=
100
cm
12
=
2
24
P=
25
3
b). P =
329
100
f
.
c)
1
f
=
f
= 12 cm
1
f
1
12
1
dioptri
3
n
 1
1 

=  2 1 

 n1
  R1 R 2 
1
12
n
 1 1 
=  2 1   
 1
  9 18 
1
12
2 1
= n 2  1   
 18 18 
1
12
3
= n 2  1 .  
 18 
1
12
1
= n 2  1 .  
6
n2 – 1 =
1 6
.
12 1
n2
1
+1
2
n2
P=8
=
= 1,5
Latihan
Kerjakan penyelesaian soal-soal berikut di buku latihanmu!
1. Sebuah lensa bikonveks (cembung-cembung) mempunyai jari-jari kelengkungan 9 cm
dan 18 cm. Sebuah benda diletakkan pada jarak 24 cm di depan lensa dan bayangan
yang terbentuk merupakan bayangan nyata 24 cm di belakang lensa itu. Tentukan
fokus, kuat lensa dan indeks bias lensa itu!
330
.
2. Sebuah lensa tipis bikonveks mempunyai jarak fokus 8 cm. Sebuah benda yang
tingginya 2 cm diletakkan di depan lensa itu. Tentukan posisi dan tinggi bayangan
yang terbentuk jika benda diletakkan pada jarak a. 12 cm dan dan b. 20 cm!
3. Sebuah lensa bikonveks (cembung-cembung) mempunyai jari-jari kelengkungan R1 =
20 cm dan R2 = 30 cm terbuat dari kaca dengan indeks bias = 1,5. Tentukan jarak
fokus lensa tersebut!
4. Sebuah lensa bikonkaf (cekung-cekung) mempunyai jari-jari kelengkungan R1 = 20
cm dan R2 = 30 cm terbuat dari kaca dengan indeks bias = 1,5. Tentukan jarak fokus
lensa tersebut!
5. Sebuah lensa konveks-konkaf (cekung-cembung) mempunyai jari-jari kelengkungan
R1 = 20 cm dan R2 = 30 cm terbuat dari kaca dengan indeks bias = 1,5. Tentukan
jarak fokus lensa tersebut!
331
.
6. Bayangan nyata yang dibentuk oleh lensa cembung-datar mempunyai ukuran 2 kali
bendanya. Jika salah satu jari-jari kelengkungan lensa yang indeks biasnya 1,52 itu
adalah 52 cm, tentukan jarak benda di depan lensa!
7. Sebuah lensa dengan indeks bias 1,5 mempunyai jarak fokus 20 cm di udara. Hitung
jarak fokusnya jika lensa tersebut dicelupkan dalam air n = !
8. Sebuah lensa bikonveks (cembung-cembung) mempunyai jari-jari kelengkungan 80
cm dan 40 cm terbuat dari kaca (n = 1,56). Hitunglah jarak fokus dan kuat lensa!
7. Pembiasan Dua Lensa yang Berhadapan
Apabila sebuah benda AB terletak di antara dua lensa yang berhadap-hadapan, akan
mengalami dua kali proses pembiasan oleh lensa I dilanjutkan oleh lensa II.
Lensa I :
1
1 1
  1
f1 s1 s1
M1 
Lensa II :
s11
s1
M2 
jarak kedua lensa :
d  s11  s 2
Perbesaran bayangan akhir :
M = M 1 . M2
M
s11 s12
.
s1 s 2
332
1
1
1

 1
f 2 s2 s2
s 12
s2
.
Contoh
Dua lensa cembung A dan B yang masing-masing berjari-jari 40 cm disusun saling
berhadapan dengan sumbu utama dan pusat kelengkungannya berhimpit. Sebuah
benda diletakkan 25 cm di depan lensa A.
Tentukan
(a) jarak bayangan benda yang dibentuk oleh lensa A
(b) jarak bayangan benda yang dibentuk oleh lensa B
(c) perbesaran bayangan total!
Penyelesaian:
Diketahui:
RA = 40 cm = RB = 40 cm
d = RA + RB = 80 cm
s A = 25 cm
Ditanya:
a. s'A ?
b. s'B ?
c. MTotal ?
Jawab:
a.
333
.
s'A = 100 cm
b.
d = s’A + sB
80 = 100 + sB
sB = 80 – 100 =  20 cm
s'B = 10 cm.
c.
Kegiatan Percobaan Mandiri
Tujuan :
Untuk menyelidiki jarak fokus dan sifat-sifat bayangan yang dibentuk oleh lensa
cembung lakukanlah eksperimen berikut ini.
Alat dan Bahan :
334
.
1 = Bangku optik
2 = Lilin sebagai benda
3 = Lensa cembung
4 = Kertas putih sebagai layar
Petunjuk Teknis :

Aturlah posisi lensa dan lilin pada jarak tertentu (s). Pastikan bayangan lilin
terbentuk di layar.

Carilah bayangan api lilin yang tampak paling terang di layar lalu ukurlah jarak
dari lilin ke layar yang merupakan jarak bayangan (s’).

Amati pula bayangan api kecil pada layar, apakah tampak terbalik atau tegak,
diperbesar atau diperkecil.

Lakukanlah langkah-langkah di atas berulang-ulang untuk jarak benda (s) yang
berbeda-beda. Masukkan data yang Kamu peroleh ke dalam table..
B. Alat-Alat Optik
1. M a t a
335
.
Kegunaan dari peralatan optik adalah untuk memperoleh penglihatan yang
lebih baik, karena mata dapat dipandang sebagai alat optik maka pembahasan tentang alat
optik di mulai dari mata sebagai alat optik alami.
Gambar 35
Mata sebagai alat
optik
a. Bagian-bagian mata
Mata merupakan salah satu organ tubuh yang sangat penting dan merupakan bagian dari
lima panca indera kita. Tanpa mata orang tidak akan pernah menikmati keindahan dunia
ini. sudah sewajarnyalah kita patut bersyukur kepada Tuhan yang telah memberi anugrah
yang luar biasa ini. dengan bantuan mata kita dapat membedakan benda berdasarkan
tingkat kecerahan, bentuk, tekstur, kedalaman, tingkat tembus pandang, gerakan dan
ukuran benda.
Dilihat dari bagian-bagian mata, mata dapat diumpamakan sebagai sebuah kamera.
Berikut ini merupakan bagian-bagian mata.
336
.
Keterangan:

Sklera atau selaput putih merupakan bagian luar yang melindungi susunan mata
bagian dalam yang lembut.

Retina adalah bagaian syaraf yang sangat sensitif terhadap cahaya.

Lensa mata (lensa cembung) berfungsi untuk memusatkan cahaya yang masuk
ke dalam mata

Iris merupakan bagian otot yang dapat mengatur sinar yang masuk ke mata,
menambah atau mengurangi cahaya yang masuk ke mata.

Pupil (biji mata) yaitu lubang yang memungkinkan cahaya masuk

Kornea merupakan lapisan pelindung mata yang jernih

Syaraf optik atau syaraf penglihatan berfungsi untuk menghantarkan sinyalsinyal (isyarat-isyarat) listrik ke otak. Di otak sinyal tersebut diolah, kemudian
timbul pesan informasi dari apa yang dilihat.
b. Pembentukan Bayangan Benda pada Retina
Beberapa istilah yang perlu diketahui terlebih dahulu pada mata diantaranya:
1. Daya Akomodasi
: Daya menebal dan menipisnya lensa mata, lensa paling
tipis pada saat mata tidak berakomodasi.
2. Titik Jauh (Punctum Remotum
: Titik terjauh yang masih terlihat jelas oleh mata
(tidak berakomodasi). Untuk mata normal : titik
jauh letaknya di jauh tak terhingga.
3. Titik Dekat (Punctum Proximum) : Titik terdekat yang masih terlihat jelas oleh mata
(berakomodasi max ). Untuk mata normal : titik
dekat 25 cm.
337
.
Ketika kita melihat suatu benda, berkas cahaya yang dipantulkan benda masuk ke mata
kita dan oleh lensa mata (lensa kristalin) berkas cahaya itu akan difokuskan sehingga
bayangan yang terbentuk akan tepat jatuh di retina. Oleh karena jarak antara mata dan
lensa selalu tetap, maka untuk melihat benda yang jaraknya berbeda-beda kecembungan
lensa mata perlu diubah-ubah. Kemampuan otot siliar untuk mengubah kecembungan
lensa mata ini disebut daya akomodasi mata. Daerah penglihatan mata seseorang sangat
dipengaruhi oleh kemampuan mata untuk mengubah kecembungan mata orang tersebut.
Orang normal akan dapat melihat benda sedekat-dekatnya pada jarak rata-rata 25 cm
dengan menggunakan daya akomodasi maksimum dan akan melihat sejauh-jauhnya
hingga jarak yang tak terhingga dengan menggunakan daya akomodasi minimum. Jarak
terdekat yang dapat dilihat seseorang disebut titik dekat mata (punctum proximum)
sedangkan titik terjauh yang masih dapat dilihat mata disebut (punctum remotum).
Berikut ini gambar pembentukan bayangan benda pada retina, lensa mata berfungsi
sebagai lensa cembung.
Bayangan benda
Benda
Gambar 37. Proses pembiasan cahaya pada
mata
Perhatikan diagram pembiasan cahaya pada mata berikut ini.
F
2F
F
2F
O
Gambar 38: Pembiasan cahaya pada mata
338
.
Semua benda yang teramati terletak di ruang III yaitu berjarak lebih besar dari 2 F.
Sifat-sifat bayangan yang terbentuk di retina :
1. Nyata
2. Terbalik
3. Diperkecil
4. Di ruang II
Perhitungan untuk hubungan antara jarak fokus mata, jarak benda dan jarak bayangan
benda atau jarak retina ke lensa mata dapat menggunakan rumus sebagai berikut.
1
f
=
1 1

s s'
Latihan.
1. Sebutkan bagian-bagian mata yang berfungsi sebagai bagian dari kamera!
2. Sebutkan nama bagian dan kegunaan dari bagian mata yang berwarna putih, biru,
orange, kuning dan abu-abu dari penampang mata berikut ini!
3. Tentukan sifat-sifat bayangan benda yang terbentuk pada retina.
4. Sebuah benda dilihat oleh mata normal yang memiliki jarak fokus 5 cm pada
jarak 4 meter. Tentukan jarak retina ke lensa mata!
5. Bagaimana bayangan yang terjadi jika benda yang diamati mata terletak di ruang
II (antara F dan 2F) ?, di ruang I (antara O dan F)?
339
.
c. Cacat Mata
Mata normal (Emetropi) adalah mata yang dalam keadaan istirahat tidak berakomodasi
bayangan jatuh tepat pada retina dan memiliki titik dekat 25 cm, serta titik jauh tak
terhingga ().
Mata dinyatakan cacat biasanya karena berkurangnya daya akomodasi mata atau kelainan
bentuk mata. Seseorang yang mengalami kelainan atau ketidak normalan pada daya
akomodasi matanya misalkan tidak bisa melihat jauh, tidak bisa melihat dekat atau tidak
mampu membedakan garis lurus maka orang tersebut dikatakan mengalami cacat mata
atau ametropi. Cacat mata semacam ini dapat ditolong dengan menggunakan kaca mata,
lensa kontak ataupun dengan jalan operasi.
1) Rabun Jauh (Miopi)
Seseorang yang menderita rabun jauh atau dikatakan berpenglihatan dekat (terang dekat)
biasanya memiliki titik jauh yang terbatas sedangkan titik dekatnya tidak berubah. Hal ini
terjadi karena lensa mata kurang mampu memipih sebagaimana mestimya sehingga sinarsinar sejajar yang berasal dari benda jauh akan berpotongan di depan retina.
Berkas cahaya berpotongan di depan retina
Gambar 39. Pembiasan cahaya
pada mata miopi (rabun jauh)
340
.
Agar dapat melihat normal orang yang mengalami cacat mata ini dapat ditolong dengan
menggunakan kaca mata berlensa negatif (divergen) dengan kekuatan lensa sebesar
P
100
f
1 1 1
= 
S S'
f
1
1 1
= 
, dimana f ( satuan cm.)
~  PR
f
atau P  
1
, f ( satuan meter.)
f
P : kekuatan lensa (Dioptri)
S=~ ,
PR : titik jauh mata (cm) ,
S’ = -PR
Contoh:
Seseorang memiliki titik jauh 200 cm. Berapakah kekuatan lensa kaca mata orang
tersebut agar ia dapat melihat dengan normal.
Penyelesaian :
Diketahui:
PR= (titik jauh) = 200 cm, S = ~ , S’ = - PR = -200
Ditanya :
P = ….dioptri
Jawab
P
100
f
1 1 1
= 
S S'
f
1
1 1
= 
~  PR
f
341
.
1
1 1
= 
~  200
f
1
1
= 0
 200
f
f = -200 cm
P
100
= - 0,5 dioptri
200
2) Rabun Dekat (Hipermetropi)
Seseorang yang menderita rabun dekat atau dikatakan berpenglihatan jauh (terang jauh)
biasanya memiliki titik dekat lebih dari 25 cm, sedangkan titik jauhnya tidak berubah
tetap pada jarak yang tak terhingga. Hal ini terjadi karena lensa mata kurang mampu
mencembung sebagaimana mestinya sehingga berkas cahaya yang datang dari jarak dekat
akan berpotongan di belakang retina.
Rabun Dekat
Berkas cahaya berpotongan di belakang retina
Gambar 40 Pembiasan cahaya pada mata
hipermetropi (rabun dekat)
Agar dapat melihat normal kembali maka penderita cacat mata ini dapat ditolong dengan
menggunakan kaca mata berlensa positif (konvergen) dengan kekuatan lensa sebesar
P
100
, f dalam cm
f
342
.
atau P 
1
; dimana f dalam satuan m.
f
Untuk menentukan nilai f dapat dihitung dengan rumus lensa
1 1 1
= 
S S'
f
1 1
1
= 
f s  PP
dengan
P
: kekuatan lensa (dioptri)
s
: jarak titik dekat mata rata-rata orang normal (25cm)
atau jarak benda yang diinginkan
PP
: jarak titik dekat mata orang yang cacat (cm)
S’ = -PP
Contoh:
Seseorang penderita rabun dekat (hipermetropi) mempunyai titik dekat 50 cm. Berapa
kuat lensa kaca mata yang harus digunakan agar:
a. ia dapat membaca pada jarak normal.
b. Ia dapat melihat dengan jelas benda yang berjarak 30 cm di depan mata.
Penyelesaian :
Diketahui : PP = 50 cm.
Ditanya : P = .... dioptri (kuat lensa)
Jawab: a. S = 25 cm ( jarak benda normal)
1
1
1

=
25  PP
f
343
.
1
1
1
2
1
1


=
=
=
25  50 50  50 50
f
1
f
=
1
50
f = 50 cm.
jadi P =
100
= 2 dioptri
50
b. S = 30 cm
1
1
1

=
f 30  PP
1
1
5
3
2
1


=
=
=
f 30  50 150 150 150
1
f
=
2
150
f = 75 cm
jadi
3)
P=
100
= 4/3 dioptri
75
Mata Tua (Presbiopi)
Seiring bertambahnya umur kemampuan mata seseorang untuk mencembung dan
memipihkan lensa mata semakin berkurang. Oleh karena itu, letak titik dekat maupun
titik jauh mata akan bergeser pula. Titik dekat presbiopi lebih besar dari 25 cm dan titik
jauh presbiopi berada pada jarak tertentu, sehingga orang tersebut tidak bisa melihat
dengan jelas baik pada jarak dekat atupun pada jarak yang jauh.
Penderita cacat mata ini dapat ditolong dengan menggunakan kacamata berlensa rangkap
atau kacamata bifokal ( kacamata dua fokus)
+
+
344
Gambar 41:
Kacamata bifokal
.
4)
Astigmatisme (Silindris)
Orang yang menderita cacat mata silindris tidak mampu melihat garis garis yang vertikal
atau horisontal secara bersama-sama. Hal ini disebabkan karena lensa mata tidak
berbentuk sferik (irisan bola) melainkan agak melengkung di bagian tertentu. Cacat mata
astigmatisme juga memfokuskan sinar sinar pada bidang vertikal lebih pandak daripada
sinar-sinar pada bidang horisontal.
Penderita cacat mata ini dapat ditolong dengan bantuan kacamata silindris sehingga dapat
membentuk bayangan yang jelas pada bagian retinanya.
Gambar 42. katarak pada mata bukanlah
cacat mata karena kelainan daya
akomodasi mata, melainkan karena
pengapuran pada kornea mata
Info sains
Lensa kontak
adalah lensa yang diletakkan
di atas kornea. Melihat fungsinya yang
multifungsi, selain menolong mata untuk
melihat lebih jelas, juga untuk mempercantik
penampilan, tak mengherankan jika akhirnya
banyak yang memilih lensa kontak
ketimbang kacamata.
Latihan
345
.
Kerjakan di buku latihanmu!
1.
Seseorang penderita miopi memiliki titik jauhnya 100 cm. Berapa kekuatan lensa kaca
matanya agar dapat melihat benda yang jauh.
2. Titik dekat mata seorang siswa terletak pada jarak 120 cm di depan mata. Untuk dapat
melihat dengan jelas suatu benda yang berjarak 30 cm di depan mata, berapa kekuatan
lensa kaca mata yang ia perlukan.
3. Pak Pris, seorang guru fisika memakai kaca mata lensa rangkap (bifocal) dengan ukuran
– 0,5 dioptri dan 2 dioptri. Jika Pak Pris melepas kaca matanya berapa jarak terdekat dan
terjauh yang dapat dilihat dengan jelas oleh matanya.
2. Kamera
Untuk merekam gambar suatu obyek, tempat, atau peristiwa orang biasanya
menggunakan kamera. Bagian-bagian pada kamera sangat mirip dengan mata. Lensa
kamera sama fungsinya dengan lensa mata yang berfungsi untuk memfokuskan
bayangan, diafragma kamera sama fungsinya dengan pupil yang berfungsi sebagai
pengatur cahaya yang masuk, film pada kamera sama fungsinya dengan retina pada mata.
Perbedaan yang ada hanya pada cara memfokuskan bayangan. Pada lensa mata punya
daya akomodasi untuk mencembung dan memipihkan lensa tetapi kalau pada kamera
untuk dapat memfokuskan bayangan lensa harus diubah-ubah jaraknya terhadap film.
Bagian-bagian penting dari kamera adalah:
a. Diagfragma berfungsi, mengatur banyak sedikitnya cahya yang masuk ke
lensa.
b. Lensa, berfungsi membiaskan cahaya.
c. Shutter, berfungsi meindungi film dari cahya luar. Shutter membuka
bersamaan dengan tombol on ditekan.
d. Film berfungsi sebagai tempat terbentuknya bayangan.
346
.
Gambar 43: Kamera
Gambar 44. Penampang kamera
Lensa
film
Benda
bayangan
Gambar 45: Hasil gambar dari sebuah
kamera, peluru yang ditembakkan pada
telur
Gambar 46: Lintasan Berkas cahaya pada kamera
Perhatikan diagram pembiasan cahaya pada kamera berikut ini.
F
2F
F
O
347
2F
.
Gambar 47: Pembiasan cahaya pada kamera
Semua benda yang teramati terletak di ruang III yaitu berjarak lebih besar dari 2 F.
Sifat-sifat bayangan akhir kamera pada film.
a. Nyata
b. Terbalik
c. Diperbesar
d. Diruang II
Pada kamera berlaku rumus lensa,
1 1 1
= 
S S'
f
Kekuatan lensa dirumuskan sebagai berikut :
dan perbesarannya : M =
p
S'
h'
=
S
h
1
, satuannya m-1 atau dioptri.
f
a. Kamera Pin hole
Sebuah kamera yang sederhana terbuat dari karton
Pin
h’
h
S
Gambar 48: skema kamera pinhole
Pada kamera pinhole juga berlaku persamaan sebagai berikut.
h
s
=
s'
h'
h , h’ = tinggi benda dan tinggi bayangan
s, s’ = jarak benda dan jarak bayangan
348
S’
.
Contoh Soal:
Sebuah kamera pin hole digunakan untuk melihat sebuah gedung yang tingginya
15 m. Jika jarak kamera ke gedung 60 m dan panjang kamera 25 cm. Hitunglah
tinggi bayangan gedung pada kamera.
Penyelesaian :
Diketahui : h = 15 m, S = 60 m, s’ = 25 cm, 0,25 m
Ditanya : h’ = ….?
Jawab :
S
15
h
60
= →
=
→ h’ = 0,0625 m = 6,25 cm
S'
h'
h'
0,25'
b. Kamera Digital
Pada jaman sekarang banyak digunakan kamera digital yang tidak menggunakan
lensa maupun prisma. Sehingga tidak terjadi proses pembiasan cahaya. Fungsi
peralatan optika untuk merekam objek digantikan dengan peralatan elektronik
digital dengan layer LCD.
Gambar 49. Kamera Digital
Latihan.
Kerjakan di buku latihanmu!
1. Sebutkan ciri-ciri atau bagian-bagian kamera serta fungsinya masing-masing.
349
.
2. Sebuah pohon mangga setinggi 3 m. Hitunglah tinggi bayangan pohon dalam
kamera pin hole ketika jarak pohon dan kamera 15 meter . Panjang kamera 20
cm.
3. Kamera dengan lensa cembung mempunyai jarak focus 50 mm. Kamera
tersebut digunakan untuk mengambil gambar photo sebuah gedung yang
berjarak 100 m dari kamera. Jika tinggi gedung yang tercetak dalam film 50
mm. Hitunglah tinggi gedung yang sebenarnya.
3. Lup (Kaca Pembesar)
Alat optik yang paling sederhana adalah lup atau kaca pembesar (magnifying
glass). Lup terdiri dari sebuah lensa cembung yang biasa digunakan untuk
memperbesar benda-benda kecil sehingga tampak menjadi besar dan lebih jelas.
Gambar 50. Pembiasan cahaya pada lup
Lup terdiri dari sebuah lensa cembung. Gunanya untuk melihat benda-benda kecil agar
tampak lebih besar dan jelas.
Dalam penggunaan lup seseorang harus menempatkan benda yang akan dilihat pada
ruang satu (antara lensa dan fokus lensa) sehingga akan dihasilkan bayangan yang
diperbesar dan maya.
350
.
Benda yang diamati harus diruang I
2f
f
0f
2f
jadi
s f
jika s < f dikatakan lensa mata berakomodasi
•
2F
•A
F
O
•
F
2F
•
•
Gambar 51: Pembisan cahaya pada lup
Sifat bayangan pada lup adalah sebagai berikut.
 maya,
 tegak,
 diperbesar,
 di ruang IV
Perbesaran yang dihasilkan oleh lup adalah perbesaran anguler atau perbesaran sudut
yang besarnya secara umum di tuliskan dalam persamaan
 1
1
d 
 dengan
M   s n 
 
  s' d f  s' d 
Mγ
: perbesaran sudut lup
PP : titik dekat mata , PR: titik jauh mata
s’
: jarak bayangan ke lup
,d : jarak mata ke lup ,f : jarak fokus lup
catatan:
1. Untuk Mata berakomodasi maksimum maka  s'd  PP, bayangan jatuh pada titik
dekat mata (PP)
2. berakomodasi pada jarak x maka  s'd  x bayangan jatuh pada titik x
351
.
3. tak berakomodasi maka  s'd  PR, bayangan jatuh pada titik jauh mata (PR)
4. Untuk mata menempel pada kaca lup atau d ( jarak mata ke lup) diabaikan maka
rumus perbesaran (M) menjadi :

M=

M=
Untuk Mata berakomodasi maksimum
25
h'
+ 1. dimana M = Perbesaran Lup dan M =
h
f
Untuk Mata tidak berakomodasi
25
, f = titik fokus lup (dalam satuan cm)
f
Contoh:
Sebuah lup mempunyai kekuatan 10 dioptri. Hitunglah tinggi bayangan benda, jika Lup
tersebut digunakan untuk mengamati benda yang tingginya 50 mm. dengan mata :
a. berakomodasi maksimum
b. tidak berakomodasi
Penyelesaian
Diketahui : P = 10 dioptri, h = 50 mm
P
f=
Ditanya :
100
f
100 100
=
= 10 cm
P
10
h’ = ….?
Jawab : a. berakomodasi maksimum
M=
h'
→h’ = M . h
h
M=
25
+1
f
352
.
M=
25
+ 1 =3,5
10
h’ = M . h = 3,5 . 50 mm = 175 mm
b.tidak berakomodasi
M=
h'
→h’ = M . h
h
M=
25
25
→M=
=2,5
10
f
h’ = M . h = 2,5 . 50 mm = 125 mm
Latihan
Jawablah di buku latihanmu!
1. Sebutkan fungsi atau kegunaan dari alat lup
2. Tentukan dimana letak benda (ruang I, II, III atau IV) terhadap lup dan
bagaimanakah sifat-sifat bayangan yang dihasilkan oleh lup.
3. Salah satu peralatan bagian mesin jam tangan berukuran 3 mm. Jika diamati
dengan sebuah lup yang mempunyai titik focus 2,5 cm, maka tentukan ukuran
alat mesin tersebut untuk mata :
a. berakomodasi maksimum
b. tidak berakomodasi
4. Mikroskop
Untuk melihat benda-benda yang sangat kecil atau renik tidak cukup hanya dengan lup
saja. Untuk itu dalam penelitiannya Antonie Van Leeuwenhoek (1632-1723) menemukan
sebuah alat yang dapat digunakan untuk mengamati benda-benda renik yang disebut
dengan mikroskop.
Sebuah mikroskop terdiri atas susunan dua buah lensa cembung. Lensa cembung yang
dekat dengan denda yang diamati disebut dengan lensa obyektif, sedangkan lensa yang
353
.
dekat dengan mata disebut dengan lensa okuler. Jarak fokus lensa okuler dibuat lebih
besar daripada lensa obyektifnya.
Bagaimanakah cara kerja mikroskop ? Ketika melakukan pengamatang dengan
menggunakan mikroskop maka benda harus diletakkan di antara fob dan 2fob
(fob
<sob<fob). Bayangan yang dibentuk oleh lensa obyektif selanjutnya dipandang sebagai
benda okuler dan terletak antara titik optik lensa okuler O dan fokus okuler fok
Gambar 52. Mikroskop
Gambar 53. Pembiasan cahaya pada mikroskop
Sebuah mikroskop selalu memiliki jarak fokus okuler (fok) yang lebih besar dari pada
jarak fokus obyektif ( fob)
Jadi,
fok  fob
354
.
Perhatikan diagram pembiasan cahaya pada mikroskop sebagai berikut.
Ob
Ok
Fob
2Fob
Fob
2Fob
Fok
O
O
2Fok
Gambar 53: Pembiasan cahaya pada mikroskop
Semua benda yang diamati pada mikroskop terletak di ruang II lensa obyektif yaitu untuk
membentuk bayangan di ruang III lensa obyektif setelah dibiaskan oleh lensa obyektif.
Bayangan ini dianggap benda oleh lensa okuler dan terletak di ruang I lensa okuler.
Akhirnya bayangan akhir terbentuk di ruang IV lensa okuler setelah mengalami
pembiasan lensa okuler.
Sifat bayangan akhir pada mikroskop adalah:
 maya,
 terbalik,
 diperbesar,
 di ruang IV okuler atau 
Perbesaran lensa obyektif adalah perbesaran linier lensa positif
dinyatakan sebagai
355
yang besarnya
Fok
.
M ob 
h' ob  s' ob

h ob
s ob
dengan
h’ob
: tinggi bayangan obyektif
hob : tinggi benda obyektif
s’ob
: jarak bayangan obyektif
sob : jarak benda obyaktif
Mob
: perbesaran lensa obyektif
Perbesaran lensa okuler mikroskop (Mok) sama seperti perbesaran lup. perbesaran
totalnya adalah
M tot  M ob .M ok
Sedangkan untuk jarak antara lensa obyektif dan lensa okuler mikroskop adalah d yang
besarnya sebagai berikut.

Untuk mata berakomodasi maksimum
Bayangan hasil pembiasan lensa obyektif terletak di antara titik fokus lensa okuler
dengan titik pusat lensa okuler, sehingga s’ok  fok.
d  s' ob s ok dan

M total = S ob ' x
S ob
 PP 

 1
f
 ok

Untuk mata tak berakomodasi
Bayangan hasil pembiasan lensa obyektif
sehingga s’ok = fok
tepat terletak di titik fokus lensa okuler
dan s’ ok = tak terhingga.
d  s' ob f ok dan
M total =
S ob '
x
S ob
356
 PP 


 f ok 
.
5. Teropong atau Teleskop
Untuk dapat melihat benda-benda
yang agak jauh dan agar terlihat
jelas,
seperti
pemandangan
gunung,
laut
kita
dapat
menggunakan teropong, sedangkan
untuk melihat benda-benda yang
sangat jauh, seperti bintang, bulan
kita
menggunakan
teleskop.
Berbagai contoh teropong adalah
teropong panggung, teropong
bumi..
Gambar 54. Keker atau teropong prisma
Teleskop atau alat untuk mengamati benda-benda yang jauh biasanya terdiri dari :
-
Sebuah lensa (+), sebagai lensa okuler , yaitu lensa yang dekat dengan mata.
-
Sebuah lensa (+), sebagai lensa obyektif, yaitu lensa yang menghadap obyek
Ciri teleskop jarak fokus obyektif  jarak fokus okuler .
fob  f0k
a. Teropong Bintang
Teropong bintang mempergunakan dua lensa cembung / positif yaitu :
- lensa obyektif
- lensa okuler
Benda yang diamati terletak jauh tak terhingga, sehingga bayangan jatuh pada fokus
obyektif.
Titik fokus obyektif berimpit dengan titik fokus okuler. Jarak fokus obyektif lebih
besar dari jarak fokus okuler.

Mata tak berakomodasi
357
.
Bintang, sebagai benda terletak jauh tak terhingga s0b= ~ bayangan dari lensa
obyektif di fob. Titik fokus okuler berimpit dengan fokus obyektif. Bayangan dari
obyektif sebagi benda pada lensa okuler.
Jadi sok = fob dan sob = fob dan
sok = fok serta s1ok= ~
Rumus perbesaran bayangan adalah sebagai berikut.
f ob
f ok
M=
Panjang teleskop = jarak antara obyektif dan okuler
d = s10b + s0k atau d = f0b + f0k
Perhatikan diagram berikut ini.
Ob
Ok
2fok

Fob

O
fok

O

fob
fok
2fok


2fob
Gambar 55. Pembiasan cahaya pada teropong
bintang dengan lensa mata tidak berakomodasi
Sifat bayangan akhir pada teropong bintang untuk mata tidak berakomodasi adalah:
 maya,
 terbalik,
 diperbesar,
 di tak terhingga 
358
.

Mata berakomodasi
Benda pada jarak jauh sekali s0b= ~ , sehingga bayangan lensa obyektif terletak pada
titik fokus obyektif sehingga s0b = f0b. Bayangan tersebut sebagai benda lensa okuler .
Jadi benda lensa okuler di ruang I lensa okuler. s0k = di ruang I. Bayangan okuler di
ruang IV lensa okuler atau s10k=  PP
Rumus perbesaran bayangan adalah sebagai berikut.
f ob
sok
M=
Panjang teleskop = jarak antara obyektif dan okuler
d = s10b + s0k atau
d = f0b + s0k
Perhatikan diagram pembiasan cahaya berikut ini.
Ob
Ok
fok

Fob

O
fok
 
O

fok

fob
2fok

2fob
Gambar 56: Pembiasan cahaya pada teropong bintang
untuk lensa mata berakomodasi
Sifat bayangan akhir pada teropong bintang untuk mata berakomodasi adalah:
359
.
 maya,
 terbalik,
 diperbesar,
 di ruang IV okuler
b. Teropong Bumi
Prinsip dari teropong ini sama dengan teropong bintang, perbedaannya terletak pada
bayangan terakhirnya (yaitu tegak). Untuk itu harus dipasang lensa pembalik.
Oleh karena itu, teropong ini terdiri dari 3 buah lensa yaitu :
-
lensa obyektif
: terdiri dari lensa positif
-
lensa cembung
: berfungsi sebagai lensa pembalik
(terletak antara lensa obyektif dan lensa okuler)
-
lensa okuler

:
terdiri dari lensa positif dan berfungsi sebagai lup
Untuk mata tidak berakomodasi
Benda terletak di jauh tak terhingga jadi s0b = ~ , bayangan dari lensa obyektif s10b = f0b
jatuh di titik fokus lensa obyektif dan berimpit dengan titik pusat kelengkungan lensa
pembalik. Lensa pembalik berfungsi membalikkan sifat bayangan, menjadi tegak dengan
perbesaran 1, sehingga Mp =1.
Titik fokus okuler berimpit dengan titik pusat kelengkungan lensa pembalik. Bayangan
dari lensa pembalik tepat di titik fokus okuler. S0k= f0k
Bayangan akhir dari lensa okuler jatuh di jauh tak terhingga
360
s10b= ~
.
Keadaan seperti tersebut diatas dinamakan pengamatan dengan mata tidak berakomodasi.
Perhatikan diagram berikut ini.
Ob
P
2fp


fob
O

fp
O

fp

fob
Ok
2fob

2fp

fok

O

fok
Gambar 57: Pembiasan cahaya pada teropong bumi
dengan lensa mata tidak berakomodasi
Sifat bayangan akhir pada teropong bumi untuk mata tidak berakomodasi adalah:
 maya,
 tegak,
 diperbesar,
 di tak terhingga 
Berlaku rumus :
361
.
M  M ob  M p  M ok

s 1 ob 2 f p s 1 ok


s ob 2 f p s ok

f ob ~

~
f ok
M 
f ob
f ok
1
Panjang teropong : d  sob
 s p  s1p  sok
d  f ob  2 f p  f ok
d  f ob  4 f p  f ok

Untuk mata berakomodasi
Bila sok  fok maka pengamatan dinamakan pengamatan mata berakomodasi
f ob
, d  f ob  4 f p  Sok
Sok
Berlaku : M 
Dengan catatan s1ok = PP =  25 cm
Perhatikan diagram berikut ini.
Ob
P
2fp


fob
O

fp
O

fp

fob
Ok
2fob
2fp

 

fok

O
fok
Sifat bayangan akhir pada teropong bumi untuk mata berakomodasi adalah:
Gambar 58: Pembiasan cahaya pada teropong bumi
dengan lensa mata berakomodasi
362
.
 maya,
 tegak,
 diperbesar,
 di ruang IV lensa okuler
Untuk menghindari panjang teropong bumi yang berlebihan diciptakan teropong prisma
atau sering disebut keker.
Gambar 59. Pembiasan cahaya
pada teropong prisma/keker
c. Teropong Panggung
Teropong panggung (Teropong Belanda = Teropong Tonil = Teropong Galilei)
mempunyai
lensa cembung/ positif (obyektif) dan lensa cekung/ negatif
(okuler), lensa cekung digunakan agar bayangan yang terbentuk tegak. Teropong
panggung dibuat sebagai pembaharuan dari teropong bumi (karena teropong bumi
terlalu panjang).
363
.

Mata tak berakomodasi
Pengamatan menggunakan teropong selalu dalam jangka waktu lama sehingga
menggunakan mata tak berakomodasi.
Perhatikan diagram pembiasan cahaya pada teropong panggung sebagai berikut.
Rumus-rumusnya adalah sebagai berikut.
soby  
M 
sok  f ok
f ob
f ok
Jarak antara lensa obyektif dan lensa okuler
d  f ob  f ok
dengan fok dimasukkan bertanda – (negatif) karena lensa cekung

Mata berakomodasi
Benda pada jarak jauh sekali s0b= ~ , sehingga bayangan lensa obyektif terletak pada
fokus s0b = f0b. Bayangan tersebut sebagai benda lensa okuler . Jadi benda lensa okuler di
ruang I atau s0k = di ruang I okuler
s 'ok   PP
M ok 
Perbesarannya
PP
sok
364
M 
s 'ob PP

sok
sok
.
6. Periskop
Sebuah kapal selam menggunakan alat optik, yaitu periskop. Periskop berguna untuk
melihat keadaan di atas permukaan air. Periskop memiliki dua buah prisma yang
berfungsi untuk membelokan berkas sinar dari benda yang dilihat.
Gambar60. Periskop di kapal selam
Latihan
Kerjakan di buku tugasmu!
1. Sebutkan sifat- sifat bayangan yang terbentuk pada mikroskop!
2. Berdasarkan jalannya sinar pembentukan bayangan pada mikroskop, jelaskan cara
kerja alat optik mikroskop!
3. Sebuah mikroskop dengan titik fokus lensa objektif dan okuler masing-masing 1,8 cm
dan 5cm. Jika benda berada 2 cm di bawah lensa objektif tentukan perbesaran
mikroskop untuk mata :
a. mata berakomodasi maksimum
b. tidak berakomodasi!
365
.
4. Sebutkan sifat-sifat bayangan yang terbentuk dan cara kerja dari teropong panggung
dan teropong bintang!
5. Sebuah teropong bintang dengan titik fokus objektif dan okuler masing-masing 125
cm dan 5 cm. Tentukan perbesaran teropong dan panjang teropong tersebut!
6. Apakah gunanya periskop dan bagaimana cara kerja?
Rangkuman
1. Ada dua jenis pemantulan yaitu pemantulan baur dan pemantulan teratur. Pemantulan
baur terjadi karena sinar-sinar sejajar yang datang ke suatu permukaan yang tidak rata
dipantulkan oleh permukaan itu tidak sebagai sinar-sinar sejajar. Akibatnya kita dapat
melihat benda dari berbagai arah.
2. Pemantulan teratur terjadi karena sinar-sinar sejajar yang datang ke suatu permukaan
rata dipantulkan oleh permukaan itu dalam arah sejajar pula sehingga membentuk
bayangan benda yang hanya dapat dilihat pada arah tertentu saja.
3. Cermin adalah benda yang dapat memantulkan cahaya. Cermin dibedakan atas cermin
datar dan cermin lengkung. Cermin lengkung terdiri atas cermin cekung dan cermin
cembung. Karena pemantulan, cermin dapat membentuk bayangan
4. Bayangan pada cermin dibedakan atas bayangan nyata dan bayangan maya. Bayangan
nyata dibentuk langsung oleh sinar-sinar pantul, sedangkan bayangan maya dibentuk
oleh perpanjangan sinar-sinar pantul. Bayangan nyata dapat ditangkap layar,
sedangkan bayangan maya dapat dilihat langsung pada cermin
5. Pada cermin datar bayangan selalu bersifat maya, tegak dengan ukuran sama besar
dengan bendanya, cermin cembung menghasilkan bayangan maya, tegak dan
diperkecil, sedangkan bayangan pada cermin cekung dapat bersifat nyata atau pun
maya begitu pun ukuran bayangannya dapat tegak atau terbalik, diperbesar, sama
ataupun diperkecil bergantung kedudukannya di depan cermin
6. Persamaan untuk menentukan tinggi minimal cermin datar yang ditegakkan vertikal
agar terlihat tinggi seluruh bayangan
366
.
L=½h
7.
Jumlah
bayangan
yang
dibentuk
oleh
gabungan
dua
cermin
datar
persamaan
n=
8.
360 0

1
Persamaan untuk menyatakan hubungan antara jarak fokus (f) dan jari-jari
kelengkungan (R) pada cermin lengkung
R=2f
9.
Persamaan untuk menyatakan hubungan antara jarak fokus (f) dan jarak benda (s)
serta jarak bayangan (s') pada cermin lengkung
1
1 1
= + 1
f
S S
10. Pembiasan cahaya adalah pembelokan cahaya ketika berkas cahaya melewati bidang
batas dua medium yang berbeda indeks biasnya.
11. Indeks bias mutlak suatu bahan adalah perbandingan kecepatan cahaya di ruang
hampa dengan kecepatan cahaya di bahan tersebut.
12. Indeks bias relatif merupakan perbandingan indeks bias dua medium berbeda. Indeks
bias relatif medium kedua terhadap medium pertama adalah perbandingan indeks bias
antara medium kedua dengan indeks bias medium pertama.
13. Pembiasan cahaya menyebabkan pemantulan sempurna.
14. Pada balok kaca, prisma dan lensa, berkas cahaya mengalami dua kali pembiasan.
Pembiasan menyebabkan berkas sinar yang masuk pada balok kaca mengalami
pergeseran saat keluar dari balok kaca tersebut.
Persamaan pergeseran sinar pada balok kaca
t
367
.
15. Pada prisma berkas cahaya mengalami deviasi atau penyimpangan dengan besar
sudut deviasi yang bergantung pada sudut datang berkas cahaya dan sudut bias saat
berkas cahaya itu keluar dari prisma tersebut.
Persamaan sudut deviasi prisma
D = (i1 + r2) – β
Dm = 2 i1– β
δm = (n2-1–
β
16. Pembiasan pada permukaan lengkung menyebabkan bayangan tampak lebih besar
atau lebih kecil dari yang sesungguhnya.
Persamaan permukaan lengkung
M=
s' n1
sn2
17. Lensa tipis merupakan salah satu bentuk permukaan lengkung yang memiliki dua
bidang batas dengan ketebalan yang diabaikan. Lensa tipis dibedakan berdasarkan
kemampuannya mengumpulkan atau menyebarkan berkas sinar yang melewatinya.
Dikenal adanya lensa positif (lensa cembung atau lensa konvergen) dan lensa negatif
(lensa cekung atau lensa divergen).
Persamaan lensa tipis
=
M
+
s1
h'

s
h
368
.
P=
1
f
18. Bayangan sebuah benda di depan lensa dapat bersifat nyata atau maya, tegak atau
terbalik, diperbesar atau diperkecil bergantung posisi benda dan jenis lensanya.
19. M ata

Mata Emetropi (mata normal)
PP = 25 cm
;
PR = 

Mata Miopi (mata dekat/rabun jauh) PP = 25 cm
;
PR < 

Mata Hipermetropi (rabun dekat)
PP > 25 cm
;
PR = 

Mata Presbiopi (mata tua)
PP > 25 cm
;
PR < 
20. Kaca mata

Kaca Mata lensa Negatif (Untuk orang Miopi)
s =  dan s’ = - PR

Kaca Mata lensa Positif (Untuk orang hipermetropi)
s = 25 cm dan s’ = - PP
21. Lup


Ditempel dimata :
- Tanpa Akomodasi 
M=
PP
f
- Berakomodasi maks 
M=
PP
+1
f
.Berjarak d cm dari mata:
baca
normal, D = -s’ + d
M=
PP PP PP.d


,
f
D
D. f
 D = daya akomodasi
22. Mikroskop

Berakomodasi  d = s’ob + sok
d = jarak lensa obyektif - okuler
369
PP
=
jarak
.
s 'ob PP
M= 
(
 1)
sob f ok

d = s’ob + fok
Tidak berakomadasi
M= 
s 'ob PP
(
)
sob fok
23. Teropong Bintang

Berakomodasi maks
d = fob + sok
M=

Tidak berakomodasi
f ob PP  f ok
(
)
f ok
PP
d = fob + fok
M=
f ob
f ok
Tugas Akhir Bab 6
Membuat Model Teleskop
Bentuklah kelompok terdiri 4 – 5 orang untuk melaksanakan tugas ini. Tugas ini
diselesaikan dalam waktu tujuh hari.
1. Sediakan dua batang pipa pralon yang berdiameter berbeda sedemikian sehingga
pipa yang satu dapat dimasukkan ke dalam pipa yang lain.
2. Sediakan beberapa lensa atau kaca berbentuk bundar dengan diameter bersesuaian
dengan diameter dalam pipa-pipa pralon tersebut, sedemikian sehingga lensa atau
kaca dapat masuk ke ujung pipa dengan pas.
3. Ukurlah panjang pipa sesuai dengan yang dikehendaki dan pasanglah lensa atau
kaca di ujung-ujung pipa yang berlawanan..
370
.
4. Masukkan ujung-ujung pipa yang tanpa lensa dan buatlah sistem pengganjal
sedemikian sehingga model teleskop dapat dimajumundurkan tanpa bisa lepas di
sambungannya.
Soal-soal Akhir Bab 6
Soal Pilihan Ganda
Pilihlah salah satu jawaban yang benar
1. Bagian mana yang berfungsi mengatur jumlah cahaya yang masuk ke mata adalah
nomor.…
a.
b.
c.
d.
e.
1
2
3
4
5
1
2
3
4
5
2. Pada gambar soal no 1. bagian mata yang berfungsi sebagai tempat terbentuknya
bayangan adalah nomor.…
a. 1
b. 2
c. 3
d. 4
e. 5
3. Sifat Bayangan yang terbentuknya pada mata adalah ...
a. Nyata, terbalik, dan diperkecil
b. Nyata, tegak, dan diperkecil
c. Nyata, tegak, dan diperbesar
d. Maya, tegak, dan diperbesar
e. Maya, terbalik , dan diperkecil
371
.
4. Ketika mata melihat benda yang letaknya jauh, maka.…
a. Lensa mata menipis dan mata berakomodasi
b. Lensa mata menebal dan mata tak berakomodasi
c. ensa mata menipis dan mata tak berakomodasi
d. ensa mata menebal dan mata tak berakomodasi
e. Lensa mata berakomodasi maksimum
5. Terbentuknya bayangan pada orang penderita cacat mata miopi yang benar ditujukkan
gambar .
.
a.
c.
.
b.
d.
.
e.
6. Perhatikan gambar di bawah ini!
Gambar tersebut menunjukkan pembentukan bayangan pada mata….
a. Emetrop
c. Presbiopi
b. Miopi
d. Hipermetropi
e. Silindris
7. Perhatikan gambar di samping!
Gambar tersebut menunjukkan
pembentukan bayangan pada mata….
a. Emetrop
b. Miopi
c. Presbiopi
d. Hipermetropi
e. Astigmatisma
8. Lukisan yang menunjukkan jalannya sinar pada mata hipermetropi adalah….
372
.
a.
c.
b.
d.
e.
9. Seseorang berkacamata dengan kekuatan lensa 2 dioptri. Artinya….
a. Lensa kacamatanya cekung berfokus 2 cm
b. Lensa kacamatanya cembung berfokus 2 cm
c. Lensa kacamatanya cekung berfokus 50 cm
d. Lensa kacamatanya cembung berfokus 50 cm
e. Lensa kacamatanya cekung berfokus 100 cm
10. Jarak terdekat yang masih dapat dilihat oleh mata disebut.…
a. Punctum proksimum
b. Punctum remotum
c. hipermetropi
d. miopi
e. silindris
11. Ketika melihat benda yang dekat, keadaan lensa mata.…
a. menipis dan berakomodasi maksimum
b. mencembung dan tak berakomodasi
c. menipis dan tak berakomodasi
d. mencembung dan berakomodasi maksimum
e. menipis terus menerus
12. Jarak terdekat untuk mata normal orang dewasa adalah.…cm
a.  40
b.  15
c.  25
d.  10
e.  20
373
.
13. Seorang anak menderita rabun jauh dengan titik jauhnya (Punctum Remotum) sejauh
2 m. Agar anak tersebut dapat melihat benda jauh pada normal, maka harus
menggunakan lensa yang.…
a. Cembung; dan +2 dioptri
b. Cekung; dan –2 dioptri
c. Cembung dan +0,5 dioptri
d. Cekung dan – 0,5 dioptri
e. Cembung dan + 5 dioptri
14. Seorang kakek menderita rabun dekat dengan titik dekatnya (PP) sejauh 50 cm. Agar
kakek dapat membaca pada jarak normal, maka harus menggunakan lensa yang.…
a. Cembung; dan +50 dioptri
b. Cekung; dan –50 dioptri
c. Cembung;dan +2 dioptri
d. Cekung; dan –2 dioptri
e. Cembung; dan – 5 dioptri
15
Alat optik yang digunakan untuk mengabadikan peristiwa yang penting adalah .…
a. Teropong
b. Mikroskop
c Lup
d. kamera
e. periskop
16. Bagian kamera berfungsi untuk mengatur jumlah cahaya/sinar yang masuk ke dalam
kamera adalah.…
a. Film
b. Shutter
c. Diafragma
d. Lensa
e. penutup lensa
17. Bayangan benda pada kamera terletak pada bagian….
a. Film
b. Shutter
374
.
c. Diafragma
d. Lensa
e. penutup lensa
18. Sifat bayangan yang dihasilkan oleh kamera adalah.…
a. Maya – tegak – diperkecil
b. Maya – terbalik – diperkecil
c. Nyata – tegak – diperkecil
d. Nyata – terbalik – diperkecil
e. Maya – tegak – diperbesar
19. Alat optik yang digunakan untuk melihat benda yang sangat kecil (jasad renik)
adalah.…
a. Lup
b. teropong
c. Periskop
d. Mikroskop
e. teleskop
20. Sifat bayangan akhir yang terbentuk pada alat optik mikroskop adalah.…
a. Maya, tegak, diperbesar
b. Nyata, tegak, diperbesar
c. Maya, terbalik, diperbesar
d. Nyata, terbalik, diperkecil
e. Maya, terbalik, diperkecil
375
.
21. Lukisan pembentukan bayangan benda pada mikroskop di bawah ini yang benar
adalah.…
a.
c.
b.
d.
e.
B
•
•A
•
•
•
22. Berikut ini merupakan kegiatan orang yang bekerja dengan menggunakan alat optik
lup adalah .....
a. Tukang Batu
b. Tukang servis kendaraan
c. Tukang servis jam
d. Tenaga laboratorium kesehatan
e. Peneliti bakteri
23. Letak benda yang benar terhadap lup pada gambar di bawah ini adalah ....
a.
b.
e.
●
●
M
F
●
●
M
F
●
●
M
F
O
O
O
●
c.
●
F
M
●
●
F
●
F
d.
M
●
M
376
●
●
M
F
●
●
M
F
O
O
●
F
●
F
●
M
●
M
.
24. Untuk mengamati benda yang sangat jauh seperti pemandangan gunung, burung,
maka alat optik yang akan digunakan adalah.…
a. Periskop
b. Teropong
c. Mikroskop
d. Lup
e. diaskop
25. Sifat bayangan yang terbentuk pada teropong bintang adalah.…
a. Maya, terbalik, diperbesar
b. Nyata, tegak, diperbesar
c. Maya, terbalik, sama besar
d. Nyata, tegak, sama besar
e. Nyata, terbalik, diperkecil
Soal Uraian
Kerjakan soal-soal di bawah ini dengan benar
1. Jarak focus lensa gelas ( n = 1,5 ) di dalam alkohol ( n = 1,35) ialah 45 cm. hitung
jarak fokus dan kuat lensa tersebut di udara.
2. Sebuah lensa plankonkaf mempunyai panjang fokus –25cm. Jari-jari kelengkungan
salah satu permukaannya 12 cm. Hitung indeks bias lensa.
3. Sebuah lensa konkaf konveks mempunyai jari-jari kelengkungan 10 cm dan 12 cm
terbuat dari kaca dengan indeks bias 1,6.
a. Fokus lensa
b. Kuat lensa
c. Perbesaran bayangan jika sebuah benda diletakkan pada jarak 50 cm.
4. Sebuah lensa bikonveks mempunyai jari-jari kelengkungan 9 cm dan 18 cm. Pada
jarak 24 cm ternyata bayangan yang terbentuk nyata pada jarak 24 cm dari lensa.
Hitung :
377
.
a. Jarak fokus
b. Kekuatan lensa
c. Indeks bias lensa
5. Sebuah benda diletakkan 15 cm di depan sebuah lensa bikonveks (cembungcembung) yang jari-jari kelengkungannya 12 cm dan 36 cm. Bayangan benda tersebut
berada pada jarak 75 cm dari lensa, tentukan indeks bias lensa!
6. Jarak fokus lensa di dalam larutan etil alkohol 45 cm. Hitung jarak fokus dan kuat
lensa tersebut di udara bila indeks bias lensa di udara 1,5 dan indeks bias larutan
1,35!
7. Sebuah lensa bikonkaf (cekung-cekung) mempunyai jari-jari kelengkungan 10 cm
dan 12 cm terbuat dari kaca dengan indeks bias 1,6. Tentukan jarak fokus lensa
tersebut di udara!
8. Salah satu jari-jari kelengkungan lensa plankonkaf besarnya 12 cm. Bila jarak fokus
lensa itu -22,2 cm, tentukanlah indeks bias lensa tersebut!
9. Sebuah lup yang berjarak titik api 5 cm menghasilkan bayangan maya 25 cm dari
mata. Berapakah jarak benda ? Berapakah perbesaran panjangnya ?
10. Sebuah benda yang tingginya 5 mm diamati oleh orang bermata normal dengan
memakai lup yang jarak titik apinya 4 cm.
a. Berapakah perbesaran sudutnya jika lup menghasilkan perbesaran maksimum ?
b. Berapakah perbesaran sudutnya jika bayangan maya berada 50 cm dari lensa ?
c. Berapakah perbesaran sudutnya jika bayangan maya itu berada di tempat yang
jauh tak berhingga ?
d. Berapa jarak benda ke mata jika loupe diletakkan 5 cm dari benda dan saat itu
mata berakomodasi pada jarak 45 cm, hitung pula perbesarannya.
11. Seorang bermata normal (titik dekat 25 cm) mengamati sebuah benda dengan
menggunakan sebuah lup yang jarak titik apinya 12,5 cm. Jarak antara benda dengan
lup 10 cm. Jarak antara mata dengan lup 50 cm. Berapakah perbesaran sudutnya ?
12. Berapakah panjang fokus sebuah kacamata membaca yang dipakai seseorang, kalau
orang tersebut mempunyai titik dekat 20 dm ?
378
.
13. Titik jauh sebuah mata myop adalah 30 cm. Berapakah panjang fokus kacamata yang
harus dipakai supaya dapat melihat benda-benda yang sangat jauh ?
14. a. Di mana titik dekat sebuah mata yang memakai kacamata baca 2 dioptri ?
b. Di mana titik jauh sebuah mata yang memakai kacamata -0,5 dioptri untuk
melihat jauh ?
15. Sebuah mikroskop mempunyai obyektif yang berjarak titik api 10 mm dan okuler
yang berjarak titik api 25 mm. Berapakah jarak antara kedua lensa itu dan berapakah
perbesarannya apabila bendanya berada pada jarak 10,5 mm dari obyektif dan mata
berakomodasi maksimum ?
16. Obyektif dan okuler sebuah mikroskop masing-masing mempunyai jarak titik api 2
cm. Jika sebuah benda diletakkan pada jarak 2,5 cm dari obyektif, berapakah jarak
antara obektif dan okuler untuk mata yang tidak berakomodasi dan berapakah
perbesarannya ?
17. Sebuah teropong bumi mempunyai obyektif yang berjarak titik api 1 meter. Bila
orang dengan mata normal yang tidak berakomodasi melihat ke sebuah benda di
tempat yang jauh tak hingga dengan menggunakan teropong tersebut, maka
memperoleh daya perbesaran 20 kali. Lensa pembaliknya berjarak titik api 25 cm.
Berapakah panjang teropong itu. Berapakah perbesarannya jika orang itu
berakomodasi pada 25 cm dan berapakah panjang teropongnya ?
18. Berapakah panjang maksimum dan berapa panjang minimum teropong panggung
yang mempunyai obyektif dengan jarak titik api 20 cm dan okuler yang berjarak titik
api 5 cm untuk mata normal dengan titik dekat 25 cm ? Berapakah daya perbesaran
maksimum dan berapa minimumnya bila dipakai untuk melihat benda-benda yang
berada di tempat yang jauh tak berhingga ?
19. Sebuah teropong bintang mempunyai obyektif yang berjarak titik api 250 cm dan
sebuah okuler yang berjarak titik api 2 cm. Obyektif tersebut terdiri sebuah lensa
positif yang berjarak titik api 125 cm yang dilekatkan pada sebuah lensa negatif
sehingga merupakan lensa gabungan yang sentris. Teropong itu ditujukan ke sebuha
bintang yang dilihatnya dengan mata normal yang tak berakomodasi. Berapa dioptri
kuatnya lensa negatif tadi ? Berapakah perbesaran teropong ? Kemudian teropong
digeser sedemikian sehingga seorang berpenglihatan dekat dengan titik jauh 70 cm
379
.
dapat melihat bayangan terang dengan tak berakomodasi. Berapa cm okuler itu harus
digeser dan ke mana arahnya ?
20. Sebuah teropong bumi diarahkan ke suatu benda yang berhingga jauhnya. Okulernya
terdiri dari lensa bikonvex, gelas kerona dan lensa plankoncaaf dari gelas flinta yang
ditempelkan pada lensa bikonvex tadi. Jari-jari kelengkungan dari 3 permukaan
lengkung sama besarnya yaitu 1,6 cm. Penunjuk bias lensa kerona 1,48 dan gelas
flinta 1,64. Jarak titik api obyektif 50 cm. Jarak titik api lensa pembalik 5 cm.
Ditanyakan :
a. Jarak obyektif – okuler untuk mata tak berakomodasi
b. Jarak obyektif – okuler untuk mata yang berakomodasi pada jarak 20 cm
c. Jarak dan jurusan mengisarnya okuler untuk bayangan yang terang pada sebidang
tabir yang jaraknya 15 cm di belakang okuler.
d. Lukislah untuk pertanyaan b dengan skala 1 : 5
21. Sebuah mikroskop mempunyai onyektif yang berjarak titik api 7,5 mm. Benda kecil
berada 8 cm dari obyektif. Bayangan yang terbentuk dilihat dengan okuler yang
berjarak titik api 5 cm. Pertanyaan :
a. Mata melihat bayangan terang tanpa berakomodasi. Berapa jarak obyektif dan
okuler!
b. Mata berpenglihatan dekat dengan titik jauh 20 cm dan melihat bayangan tak
berakomodasi. Berapa cm okuler harus digeser dan ke mana arahnya?
c. Lukis pembentukan bayangan pada b!
d. Mata berpenglihatan dekat tadi mengulangi penilikannya seperti hanya pada ad. a
dengan menggunakan kacamata sehingga okuler tdak harus digeser. Bila dalam
hal ini mata juga tak berakomodasi, berapa dioptrikah kacamata itu?
22. Suatu mikroskop mempunyai obektif dengan perbesaran lateral 100 kali. Berapa
panjang fokus okulernya bila mikroskop tersebut menghasilkan perbesaran 1000 kali?
23. Suatu mikroskop dilengkapi dengan obyektif-obyektif yang panjangnya 16 mm, 4
mm dan 1,9 mm dan okuler-okuler yang mempunyai perbesaran sudut 5 kali dan 10
kali. Bayangan dari obyektif 160 mm di sebelah luar titik-titik fokus kedua.
a. Berapakah perbesaran maksimumnya?
b. Berapakah perbesaran minimumnya?
380
.
24. Sebuah lup dengan titik fokus 10 cm. Digunakan untuk melihat benda setinggi
5 mm. Berapa tinggi bayangan benda ketika mata berakomodasi maksimum!
25. Sebukan sifat-sifat bayangan yang terbentuk pada film kamera!
26. Sebuah kamera pinhole digunakan untuk melihat sebuah menara lampu
mercusuar, jika jarak menara ke kamera 100 m dan panjang kamera pin hole
20 cm serta tinggi bayangan yang terbentuk 10 cm .Tentukan tinggi menara
sesungguhnya!
27. Sebuah mikroskop dengan titik fokus lensa objektifnya 2 cm. Tentukan
dimana benda harus diletakan di depan lensa objektif ( < 2 cm , 2 cm sampai
4 cm, atau lebih dari 4 cm ) dan sebutkan sifat-sifat bayangan yang terbentuk!
28. Sebutkan sifat-sifat bayangan yang terbentuk pada teropong panggung!
29. Sebuah teropong bintang dengan perbesaran 20 x. Jika titik fokus lensa
objektif 100 cm tentukan jarak titik fokus lensa okuler dan panjang teropong
tersebut!
30. Apakah gunanya prisma pada periskop? Sebutkan sifat-sifat bayangan pada periskop!
Sebuah lup yang berjarak titik api 5 cm menghasilkan bayangan maya 25 cm dari
mata. Berapakah jarak benda ? Berapakah perbesaran panjangnya ?
31. Sebuah benda yang tingginya 5 mm diamati oleh orang bermata normal dengan
memakai lup yang jarak titik apinya 4 cm. Berapakah perbesaran sudutnya jika lup
menghasilkan perbesaran maksimum? Berapakah perbesaran sudutnya jika bayangan
maya berada 50 cm dari lensa ? Berapakah perbesaran sudutnya jika bayangan maya
itu berada di tempat yang jauh tak berhingga ?
32. Berapa jarak benda ke mata jika lup diletakkan 5 cm dari benda dan saat itu mata
berakomodasi pada jarak 45 cm, hitung pula perbesarannya.
33. Seorang bermata normal (titik dekat 25 cm) mengamati sebuah benda dengan
menggunakan sebuah lup yang jarak titik apinya 12,5 cm. Jarak antara benda dengan
lup 10 cm. Jarak antara mata dengan lup 50 cm. Berapakah perbesaran sudutnya ?
34. Berapakah panjang fokus sebuah kacamata membaca yang dipakai seseorang, kalau
orang tersebut mempunyai titik dekat 20 dm ?
35. Titik jauh sebuah mata myop adalah 30 cm. Berapakah panjang fokus kacamata yang
harus dipakai supaya dapat melihat benda-benda yang sangat jauh ?
381
.
36. a. Di mana titik dekat sebuah mata yang memakai kacamata baca 2 dioptri ?
b.
Di mana titik jauh sebuah mata yang memakai kacamata -0,5 dioptri untuk
melihat jauh ?
37. Sebuah mikroskop mempunyai obyektif yang berjarak titik api 10 mm dan okuler
yang berjarak titik api 25 mm. Berapakah jarak antara kedua lensa itu dan berapakah
perbesarannya apabila bendanya berada pada jarak 10,5 mm dari obyektif dan mata
berakomodasi maksimum ?
38. Obyektif dan okuler sebuah mikroskop masing-masing mempunyai jarak titik api 2
cm. Jika sebuah benda diletakkan pada jarak 2,5 cm dari obyektif, berapakah jarak
antara obektif dan okuler untuk mata yang tidak berakomodasi dan berapakah
perbesarannya ?
39. Sebuah teropong bumi mempunyai obyektif yang berjarak titik api 1 meter. Bila
orang dengan mata normal yang tidak berakomodasi melihat ke sebuah benda di
tempat yang jauh tak hingga dengan menggunakan teropong tersebut, maka
memperoleh daya perbesaran 20 kali. Lensa pembaliknya berjarak titik api 25 cm.
Berapakah panjang teropong itu. Berapakah perbesarannya jika orang itu
berakomodasi pada 25 cm dan berapakah panjang teropongnya ?
40. Berapakah panjang maksimum dan berapa panjang minimum teropong panggung
yang mempunyai obyektif dengan jarak titik api 20 cm dan okuler yang berjarak titik
api 5 cm untuk mata normal dengan titik dekat 25 cm ? Berapakah daya perbesaran
maksimum dan berapa minimumnya bila dipakai untuk melihat benda-benda yang
berada di tempat yang jauh tak berhingga ?
41. Sebuah teropong bintang mempunyai obyektif yang berjarak titik api 250 cm dan
sebuah okuler yang berjarak titik api 2 cm. Obyektif tersebut terdiri sebuah lensa
positif yang berjarak titik api 125 cm yang dilekatkan pada sebuah lensa negatif
sehingga merupakan lensa gabungan yang sentris. Teropong itu ditujukan ke sebuha
bintang yang dilihatnya dengan mata normal yang tak berakomodasi. Berapa dioptri
kuatnya lensa negatif tadi ? Berapakah perbesaran teropong ? Kemudian teropong
digeser sedemikian sehingga seorang berpenglihatan dekat dengan titik jauh 70 cm
dapat melihat bayangan terang dengan tak berakomodasi. Berapa cm okuler itu harus
digeser dan ke mana arahnya ?
382
.
42. Sebuah teropong bumi diarahkan ke suatu benda yang berhingga jauhnya. Okulernya
terdiri dari lensa bikonvex, gelas kerona dan lensa plankoncaaf dari gelas flinta yang
ditempelkan pada lensa bikonvex tadi. Jari-jari kelengkungan dari 3 permukaan
lengkung sama besarnya yaitu 1,6 cm. Penunjuk bias lensa kerona 1,48 dan gelas
flinta 1,64. Jarak titik api obyektif 50 cm. Jarak titik api lensa pembalik 5 cm.
Ditanyakan :a. Jarak obyektif – okuler untuk mata tak berakomodasi. b. Jarak
obyektif – okuler untuk mata yang berakomodasi pada jarak 20 cm. c. Jarak dan
jurusan mengisarnya okuler untuk bayangan yang terang pada sebidang tabir yang
jaraknya 15 cm di belakang okuler.. d. Lukislah untuk pertanyaan b dengan skala 1 : 5
43. Sebuah mikroskop mempunyai onyektif yang berjarak titik api 7,5 mm. Benda kecil
berada 8 cm dari obyektif. Bayangan yang terbentuk dilihat dengan okuler yang
berjarak titik api 5 cm. Pertanyaan : a.). Mata melihat bayangan terang tanpa
berakomodasi. Berapa jarak obyektif dan okuler. b.) Mata berpenglihatan dekat
dengan titik jauh 20 cm dan melihat bayangan tak berakomodasi. Berapa cm okuler
harus digeser dan ke mana arahnya ?. c.) Lukis pembentukan bayangan pada b.
d).Mata berpenglihatan dekat tadi mengulangi penilikannya seperti hanya pada ad. a
dengan menggunakan kacamata sehingga okuler tdak harus digeser. Bila dalam hal
ini mata juga tak berakomodasi, berapa dioptrikah kacamata itu ?
44. Suatu mikroskop mempunyai obyektif dengan perbesaran lateral 100 kali. Berapa
panjang fokus okulernya bila mikroskop tersebut menghasilkan perbesaran 1000 kali.
45. Suatu mikroskop dilengkapi dengan obyektif-obyektif yang panjangnya 16 mm, 4
mm dan 1,9 mm dan okuler-okuler yang mempunyai perbesaran sudut 5 kali dan 10
kali. Bayangan dari obyektif 160 mm di sebelah luar titik-titik fokus kedua. a).
Berapakah perbesaran maksimumnya ?. b) Berapakah perbesaran minimumnya ?
GLOSARIUM
Bayangan maya : bayangan yang dibentuk oleh perpotongan dari perpanjangan sinarsinar pantul. Bayangan ini tak dapat ditangkap layar.
Bayangan nyata : bayangan yang dibentuk oleh perpotongan sinar-sinar pantul.
383
.
Bayangan ini dapat ditangkap layar.
Benda maya
: bayangan yang dianggap sebagai benda pada sistem yang terdiri dari
lebih dari satu cermin
Benda nyata
: benda yang riil, sungguh-sungguh ada
Bidang fokus
: bidang vertikal yang melalui titik fokus tegak lurus sumbu utama
Dalil Esbach
: aturan untuk menentukan sifat-sifat bayangan pada cermin lengkung
berdasarkan ruang benda dan ruang bayangan
fokus cermin
: sebuah titik pada sumbu utama tempat berkumpulnya sinar-sinar yang
dipantulkan oleh cermin cekung.
Garis normal
: garis yang melalui suatu titik pada bidang dan tegak lurus dengan
bidang tersebut
Indeks bias mutlak :perbandingan kecepatan cahaya di ruang hampa dan di suatu medium.
Indeks bias relatif :perbandingan indeks bias medium yang satu terhadap medium yang
lain.
Jarak fokus
: jarak dari pusat cermin ke fokus utama
Jari-jari kelengkungan
: jari-jari bola cermin
Kekuatan lensa : kemampuan lensa untuk mengumpulkan atau menyebarkan berkas
sinar
Lensa bikonkaf
: lensa yang kedua permukaannya merupakan lensa cekung.
Lensa bikonvek : lensa yang kedua permukaannya merupakan lensa cembung
Lensa divergen : lensa yang dapat menguraikan berkas sinar
Lensa gabungan : gabungan dua atau lebih lensa dengan sumbu utama berhimpit
Lensa konvergen: lensa yang dapat mengumpulkan berkas sinar
Lensa sferis
: lensa yang permukaannya lengkung seperti bola
Lensa tipis
: lensa yang ketebalannya diabaikan
384
.
Pemantulan baur
:pemantulan sinar pada bidang yang tidak rata
Pemantulan biasa : pemantulan sinar pada bidang yang rata
Pembiasan cahaya : pembelokan berkas cahaya saat melewati bidang batas dua medium
yang berbeda indeks biasnya.
Pusat kelengkungan
: pusat kelengkungan cermin
Sinar istimewa
: sinar datang yang lintasannya mudah diramalkan tanpa harus
mengukur sudut datang dan sudut pantulnya
Sudut datang
Sudut deviasi
: sudut yang dibentuk oleh sinar datang dan garis normal
: sudut yang dibentuk oleh berkas sinar masuk dan berkas sinar yang
keluar dari prisma.
Sudut pantul
: sudut yang dibentuk oleh sinar pantul dan garis normal
Sumbu utama
: garis yang menghubungkan pusat kelengkungan dan pusat cermin
385