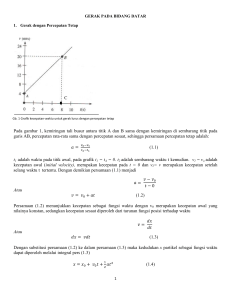
Persamaan Diferensial Biasa

Persamaan Diferensial Biasa
Rippi Maya
Maret 2014
ii
Contents
1 PENDAHULUAN
1.1 Solusi persamaan diferensial . . . . . . . . . .
1.1.1 Solusi Implisit dan Solusi Eksplisit . .
1.1.2 Solusi Umum dan Solusi Khusus . . .
1.1.3 Solusi Singular . . . . . . . . . . . . .
1.2 Masalah Nilai Awal dan Masalah Nilai Batas
1.2.1 Masalah Nilai Awal (MNA) . . . . . .
1.2.2 Masalah Nilai Batas (MNB) . . . . . .
1.3 Keujudan dan Ketunggalan Solusi . . . . . .
1.3.1 Latihan . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
2
2
3
3
4
4
5
5
8
2 Persamaan Diferensial Orde Satu
2.1 Metode Pemisahan Peubah . . . . . . . . . . . . . . . . . . . . .
2.1.1 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Metode Transformasi . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Persamaan Diferensial Eksak . . . . . . . . . . . . . . . . . . . .
2.3.1 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Faktor Pengintegral . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Menentukan faktor pengintegral . . . . . . . . . . . . . .
2.4.2 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 Persamaan Diferensial Linier . . . . . . . . . . . . . . . . . . . .
2.5.1 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6 Aplikasi Persamaan Diferensial Orde Satu . . . . . . . . . . . . .
2.6.1 Pertumbuhan Alami dan Peluruhan (Natural Growth and
Decay) . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.2 Pendinginan dan Pemanasan (Cooling and Heating) . . .
2.6.3 Bunga Majemuk (Interest Compound ) . . . . . . . . . . .
2.6.4 Eliminasi Obat (Drug Elimination) . . . . . . . . . . . . .
2.6.5 Hukum Torricelli . . . . . . . . . . . . . . . . . . . . . . .
2.6.6 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
9
11
11
13
14
16
17
19
21
22
25
25
3 Persamaan Diferensial Linier Orde Ke-n
3.1 Persamaan Diferensial Linier Homogen . . . . . . . . . .
3.1.1 Prinsip Superposisi atau Kelinieran . . . . . . . .
3.1.2 Masalah Nilai Awal . . . . . . . . . . . . . . . .
3.1.3 Latihan . . . . . . . . . . . . . . . . . . . . . . .
3.2 Persamaan dengan Koe…sien Konstanta . . . . . . . . .
3.2.1 Persaman diferensial linier homogen orde ke-dua
3.2.2 Latihan . . . . . . . . . . . . . . . . . . . . . . .
3.2.3 Persamaan diferensial linier homogen orde ke-n .
3.2.4 Latihan . . . . . . . . . . . . . . . . . . . . . . .
3.3 Persamaan Euler-Cauchy . . . . . . . . . . . . . . . . .
35
35
36
40
41
41
41
47
48
50
50
iii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
29
30
31
32
34
iv
CONTENTS
3.4
3.5
3.3.1 Latihan . . . . . . . . . . . . . . . . . . .
Persamaan Nonhomogen . . . . . . . . . . . . . .
3.4.1 Metoda Koe…sien Taktentu Orde ke-dua .
3.4.2 Metoda Koe…sien Taktentu orde ke-n . .
3.4.3 Latihan . . . . . . . . . . . . . . . . . . .
3.4.4 Metode Variasi Parameter . . . . . . . . .
3.4.5 Latihan . . . . . . . . . . . . . . . . . . .
Aplikasi Persamaan Diferensial Linier Orde Dua
3.5.1 Latihan . . . . . . . . . . . . . . . . . . .
4 Sistem Persamaan Diferensial
4.0.2 Vektor, Matriks . . . . . . . . . . . .
4.0.3 Nilai Eigen, vektor Eigen . . . . . .
4.1 Konsep Dasar dan Teori . . . . . . . . . . .
4.2 Sistem Linier Homogen . . . . . . . . . . .
4.2.1 Tak ada basis dari vektor eigen yang
4.2.2 Latihan . . . . . . . . . . . . . . . .
4.3 Sistem Linier Nonhomogen . . . . . . . . .
4.3.1 Metode Koe…sien Taktentu . . . . .
4.3.2 Latihan . . . . . . . . . . . . . . . .
4.4 Aplikasi Sistem Persamaan Diferensial . . .
4.4.1 Latihan . . . . . . . . . . . . . . . .
. . .
. . .
. . .
. . .
ada
. . .
. . .
. . .
. . .
. . .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
54
54
55
61
64
65
67
68
71
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
73
73
74
75
76
83
84
85
85
87
87
89
5 Solusi Deret Persamaan Diferensial
5.1 Metode Deret Kuasa . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.1 Deret Kuasa . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.2 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Teori Metode Deret Kuasa . . . . . . . . . . . . . . . . . . . . . .
5.2.1 Konsep Dasar . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.2 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Persamaan Legendre, Polinom Legendre Pn (x) . . . . . . . . . .
5.3.1 Polinom Legendre . . . . . . . . . . . . . . . . . . . . . .
5.3.2 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4 Metode Frobenius . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4.1 Persamaan Indisial (Indicial Equation), Menunjukkan Bentuk Solusi-solusi . . . . . . . . . . . . . . . . . . . . . . .
5.4.2 Latihan . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.5 Persamaan Bessel . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
91
91
94
94
94
98
98
100
101
101
6 Transformasi Laplace
6.1 Transformasi Laplace. . . . . . . . . . .
6.1.1 Latihan . . . . . . . . . . . . . .
6.2 Transformasi dari Turunan dan Integral
6.2.1 Latihan . . . . . . . . . . . . . .
113
113
117
118
127
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
102
107
107
A Abjad Yunani dan Rumus-rumus Trigonometri
129
A.1 Abjad Yunani . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
A.2 Rumus-rumus Trigonometri . . . . . . . . . . . . . . . . . . . . . 129
B Rumus-rumus Turunan dan Integral
131
B.1 Tabel Turunan . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
B.2 Integral Trigonometri . . . . . . . . . . . . . . . . . . . . . . . . 132
Daftar Pustaka
135
Kata Pengantar
Diktat ini disusun sebagai diktat (catatan) kuliah Persamaan Diferensial Biasa
di UIN Sunan Gunung Djati Bandung. Tujuan penulisan diktat ini adalah
untuk membantu mahasiswa Pendidikan Matematika dalam memahami materi
Persamaan Diferensial Biasa.
Ini adalah diktat revisi ke-enam, sejak pertama kali disusun pada tahun 2003.
Diktat ini terdiri dari enam bab. Bab 1 berisi tentang pendahuluan mengenai
persamaan diferensial, Bab 2 membahas mengenai persamaan diferensial orde
pertama, Bab 3 tentang persamaan diferensial linier orde yang lebih tinggi, Bab
4 mempelajari tentang sistem persamaan diferensial, Bab 5 mengkaji tentang
solusi deret persamaan diferensial dan Bab 6 mengenal transformasi Laplace.
Dalam setiap bab, soal-soal diberikan sebagai latihan bagi mahasiswa.
Keterbatasan kemampuan penulis dalam memberikan ilustrasi berupa gambar
atau gra…k, menyebabkan diktat ini masih jauh dari sempurna. Karena sifat diktat ini hanya sebagai catatan kuliah, maka penulis menyarankan agar pembaca
diktat ini juga mempelajari materi dari sumber lain, agar diperoleh pemahaman
yang lebih mendalam.
Sebagai upaya untuk terus menyempurnakan diktat kuliah ini, penulis masih
mengharapkan saran, masukan, maupun koreksi dari para pembaca. Masih dengan segala keterbatasannya, penulis berharap diktat kuliah ini dapat bermanfaat
bagi pembaca semua.
Bandung, Maret 2014
v
vi
PREFACE
Chapter 1
PENDAHULUAN
Persamaan diferensial ialah suatu persamaan yang memuat fungsi yang tak
diketahui dan satu atau beberapa turunan dari fungsi tersebut, dengan satu
atau lebih peubah yang tak diketahui. Apabila fungsi yang tak diketahui itu
hanya bergantung pada satu peubah saja, maka persamaan diferensial tersebut dinamakan persamaan diferensial biasa. Sedangkan apabila fungsinya
bergantung pada dua atau lebih peubah, maka persamaan diferensial tersebut
dinamakan persamaan diferensial parsial. Fokus pembahasan pada bab ini
dan bab-bab selanjutnya hanya pada persamaan diferensial biasa saja.
Salah satu contoh persamaan diferensial pada kehidupan sehari-hari adalah
kecepatan pertumbuhan suatu populasi, misalkan populasi dari manusia, binatang, bakteri, dan sebagainya. Jika suatu populasi tumbuh pada kecepatan
dx
x0 (t) =
(t = waktu) yang sama dengan populasi x(t) yang ada, maka
dt
model populasinya merupakan suatu persamaan diferensial, yaitu x0 = x, dengan x(t) = cet merupakan solusi dari persamaan diferensial tersebut.
Contoh yang lain adalah masalah jatuh bebas. Jika sebuah benda dijatuhkan dari
atas, maka percepatannya adalah sama dengan percepatan gravitasi g (suatu
d2 y
konstanta), yaitu : y 00 = 2
dx
(x = waktu). Model dari masalah ini adalah y 00 = g. Hasil pengintegralan
dy
pertama dari persamaan diferensial tersebut adalah kecepatan y 0 =
= gx+v0
dx
dengan v0 = kecepatan awal. Hasil pengintegralan ke-dua adalah y = 12 gx2 +
v0 x + y0 ; dengan y0 = jarak awal dari 0 (misalkan y0 = 0).
Orde dari suatu persamaan diferensial adalah orde turunan tertinggi yang terdapat pada persamaan tersebut. Persamaan diferensial orde pertama memuat
turunan pertama y 0 , mungkin pula y; dan fungsi x yang diberikan. Bentuk
umum dari persamaan diferensial orde pertama dapat dituliskan sebagai:
F (x; y; y 0 ) = 0
(1.1)
atau kadang-kadang dituliskan sebagai: y 0 = f (x; y):
Example 1 :
Perhatikan persamaan diferensial berikut ini: (1): y 0 = cos x; (2): y 00 6y =
0; (3): x3 y 000 4x2 y 00 + 8xy 0 8y = 0: Untuk persamaan: (1) ordenya adalah
1, (2) ordenya 2 dan (3) ordenya 3.
|
1
2
1.1
CHAPTER 1. PENDAHULUAN
Solusi persamaan diferensial
Sebagaimana sudah diketahui, solusi dari suatu persamaan aljabar, seperti x2 +
5x + 6 = 0; adalah suatu peubah tak diketahui x yang memenuhi persamaan
tersebut, yaitu x = 2 atau x = 3: Pada persamaan diferensial, seperti y 0 =
3xy; solusinya adalah suatu fungsi yang tak diketahui y = g(x) yang memenuhi
persamaan diferensial tersebut: Fungsi y = g(x) yang mempunyai turunan y 0 =
g 0 (x) dan memenuhi persamaan F (x; y; y 0 ) = 0; untuk semua x di dalam selang
terbuka a < x < b disebut sebagai solusi dari persamaan diferensial orde
pertama F (x; y; y 0 ) = 0:
Example 2 :
Selidiki apakah y = 2x3 merupakan solusi dari xy 0 = 3y untuk semua x.
Jawab:
Karena y = 2x3 maka y 0 = 6x2 : Dengan substitusi, diperoleh: xy 0 = x(6x2 ) =
6x3 = 3y:
Jadi benar bahwa y = 2x3 adalah solusi dari persamaan diferensial xy 0 =
3y:
|
1.1.1
Solusi Implisit dan Solusi Eksplisit
Solusi dari suatu persamaan diferensial dapat muncul dalam bentuk fungsi implisit atau fungsi eksplisit. Apabila solusi yang muncul merupakan fungsi implisit, maka solusi tersebut dinamakan solusi implisit, sebagaimana ditunjukkan oleh fungsi:
G(x; y) = 0:
Sedangkan apabila solusi yang muncul berbentuk fungsi eksplisit, maka dinamakan solusi eksplisit, sebagaimana ditunjukkan oleh fungsi:
y = g(x):
Example 3 :
Perhatikan fungsi berikut: x2 + y 2
disimpulkan dari fungsi tersebut?
4 = 0, (y > 0): Apakah yang dapat
1.1. SOLUSI PERSAMAAN DIFERENSIAL
3
Jawab:
Fungsi tersebut merupakan suatu persamaan setengah lingkaran yang berpusat
di titik (0,0) dan berjari-jari 2. Selain itu, fungsi tersebut juga merupakan solusi
implisit dari persamaan diferensial yy 0 = x , pada interval 2 < x < 2.
|
Example 4 :
Perhatikan fungsi y = 2e
3x
: Apakah yang dapat dijelaskan dari fungsi tersebut?
Jawab:
Fungsi tersebut merupakan solusi eksplisit dari persamaan diferensial y 0 + 3y =
0:
|
1.1.2
Solusi Umum dan Solusi Khusus
Solusi umum dari suatu persamaan diferensial adalah semua solusi dari persamaan diferensial tersebut yang memuat suatu konstanta sebarang c. Apabila
dari sebarang c tersebut dipilih c tertentu, maka solusi yang diperoleh merupakan solusi khusus dari persamaan diferensial tersebut.
Example 5 :
Perhatikan persamaan diferensial y 0 = sin x: Jelaskan solusi umum dan khusus
dari persamaan diferensial tersebut.
Jawab:
Solusi umum dari persamaan tersebut adalah y = cos x + c, dengan c adalah
konstanta sebarang. Apabila dipilih c tertentu, misalkan c = 2 atau c = 5 atau
c = 73 , dsb., maka akan diperoleh suatu solusi khusus dari persamaan diferensial
tersebut. Jadi y = cos x + c adalah solusi umum dari y 0 = sin x; sedangkan
y = cos x + 2; y = cos x 5, y = cos sin x + 37 dan seterusnya adalah
solusi khusus dari persamaan diferensial tersebut.
|
1.1.3
Solusi Singular
Selain solusi umum dan solusi khusus dari suatu persamaan diferensial, ada lagi
solusi lain yang merupakan solusi tambahan dari suatu persamaan diferensial.
Solusi tambahan ini tidak dapat diperoleh dari solusi umum dengan mengganti
konstanta sebarang c: Solusi tambahan yang seperti ini dikenal sebagai solusi
singular.
4
CHAPTER 1. PENDAHULUAN
Example 6 :
2
Persamaan diferensial berikut, y 0 xy 0 +y = 0 mempunyai solusi umum y(x) =
cx c2 . Persamaan ini menyatakan grup garis lurus, dengan setiap c yang dipilih
x2
menyatakan satu garis lurus. Perhatikan fungsi y(x) =
, yang merupakan
4
persamaan kuadrat dan juga merupakan solusi dari persamaan diferensial di
atas, namun bukan solusi khusus dari persamaan diferensial tersebut. Solusi ini
tidak dapat diperoleh dengan memilih c yang tepat dari solusi umumnya. Oleh
x2
disebut sebagai solusi singular dari persamaan diferensial
sebab itu, y(x) =
4
tersebut. Berikut ini adalah gra…k solusi umum: y(x) = cx c2 dan solusi
x2
.
|
singular y(x) =
4
y
5
4
3
2
1
-5
-4
-3
-2
-1
1
-1
2
3
4
5
x
-2
-3
-4
-5
1.2
1.2.1
Masalah Nilai Awal dan Masalah Nilai Batas
Masalah Nilai Awal (MNA)
Inti pembahasan dalam teori persamaan diferensial adalah apakah persamaan
diferensial tersebut mempunyai solusi atau tidak, terutama yang memenuhi
syarat-syarat tertentu. Syarat-syarat tertentu yang dimaksud adalah solusi yang
mempunyai nilai tertentu, atau kadang-kadang juga nilai turunannya pada suatu
titik tertentu. Syarat-syarat yang seperti itu disebut sebagai syarat awal. Persamaan diferensial yang disertai dengan syarat awal dinamakan dengan masalah
nilai awal (MNA).
1.3. KEUJUDAN DAN KETUNGGALAN SOLUSI
5
Example 7 :
Pandang suatu masalah nilai awal: y 0 = cos 2x, dengan y(0) = 4: Carilah solusi
masalah nilai awalnya.
Jawab:
Solusi umum dari persamaan diferensial tersebut adalah: y = 21 sin 2x + c:
Karena y(0) = 4; maka 4 = 21 sin 2:0 + c sehingga c = 4. Jadi solusi masalah
|
nilai awalnya adalah y(x) = 12 sin 2x + 4:
Example 8 :
Perhatikan persamaan diferensial y 00 + 16y = 0, dengan syarat awal y(0) = 3
dan y 0 (0) = 4: Tentukan solusi masalah nilai awalnya.
Jawab:
Solusi umum dari persamaan diferensial tersebut adalah: y(x) = A cos 4x +
B sin 4x: Karena y(0) = 3; maka 3 = A cos 0 + B sin 0 sehingga A = 3. Turunan
pertama dari solusi umum y(x) adalah y 0 (x) = 4A sin 4x + 4B cos 4x. Karena
syarat awal y 0 (0) = 4 , maka dengan substitusi diperoleh: 4 = 4A sin 0 +
4B cos 0 , sehingga B = 1. Jadi solusi masalah nilai awal dari persamaan
diferensial tersebut adalah
y(x) = 3 cos 4x
1.2.2
sin 4x:
|
Masalah Nilai Batas (MNB)
Selain masalah nilai awal, pada persamaan diferensial juga dikenal adanya
masalah nilai batas (MNB). Pada masalah nilai awal, syarat awal yang
menyertai persamaan diferensial hanya pada satu titik tertentu. Sedangkan pada
masalah nilai batas, syarat awalnya pada dua titik yang berbeda. Untuk membedakan syarat awal pada masalah nilai awal dan pada masalah nilai batas, maka
syarat awal pada masalah nilai batas disebut sebagai syarat batas.
Example 9 :
Diberikan suatu persamaan diferensial y 00 + 4y = 0, dengan syarat batas y(0) =
1; dan y( =4) = 1. Tentukan solusi masalah nilai batasnya.
Jawab:
Solusi umum dari persamaan diferensial tersebut adalah: y(x) = A cos 2x +
B sin 2x. Dari y(0) = 1 diperoleh A = 1; dan dari y( =4) = 1 diperoleh
B = 1 . Jadi solusi dari masalah nilai batas tersebut adalah y(x) = cos 2x
sin 2x.
|
1.3
Keujudan dan Ketunggalan Solusi
Dari contoh-contoh mengenai masalah nilai awal,
y 0 = f (x; y);
y(x0 ) = y0
(1.2)
yang sudah dibahas terdahulu, selalu didapatkan solusi khusus yang tunggal.
Sebenarnya solusi tunggal ini hanyalah satu dari tiga kemungkinan solusi yang
mungkin ada dalam mencari penyelesaian suatu masalah nilai awal. Sebagai
contoh, perhatikan masalah nilai awal berikut ini:
6
CHAPTER 1. PENDAHULUAN
1. jy 0 j + jyj = 0; y(0) = 1:
Satu-satunya solusi untuk masalah nilai awal tersebut adalah y = 0: Karena
syarat awal yang diberikan tidak dapat diterapkan ke dalam solusi tersebut,
maka masalah nilai awal ini tidak mempunyai solusi.
2. y 0 = x; y(0) = 1:
Solusi untuk masalah nilai awal tersebut adalah y = 12 x2 + 1; yang merupakan
solusi tunggal.
3. xy 0 = y
1; y(0) = 1:
Solusi untuk masalah nilai awal tersebut adalah y = cx + 1; dengan c konstanta
sebarang. Karena solusi dari masalah nilai awal ini bergantung kepada pemilihan konstanta c; maka akan diperoleh banyak solusi untuk masalah nilai awal
tersebut.
Dari contoh-contoh di atas diketahui bahwa suatu masalah nilai awal dapat
mempunyai satu solusi, banyak solusi atau bahkan mungkin tidak mempunyai
solusi. Selama ini, dari contoh-contoh yang sudah dibahas, bentuk masalah nilai awalnya masih sederhana, sehingga dengan mudah dapat diketahui solusinya
dengan tepat. Bagaimana kalau bentuk masalah nilai awalnya tidak sederhana
lagi atau lebih kompleks? Untuk mengetahui solusi yang tepat dari ketiga kemungkinan solusi tersebut, diperlukan suatu petunjuk yang menerangkan kondisikondisi suatu masalah nilai awal agar mempunyai satu solusi, banyak solusi
atau tidak ada solusi. Dengan kata lain, pada kondisi yang bagaimanakah suatu masalah nilai awal mempunyai paling sedikit satu solusi atau paling banyak
satu solusi? Ada dua teorema yang menjelaskan mengenai kondisi-kondisi tersebut. Teorema yang menjelaskan kondisi suatu masalah nilai awal mempunyai
paling sedikit satu solusi, disebut Teorema Ketunggalan. Sedangkan teorema
yang menjelaskan kondisi suatu masalah nilai awal mempunyai paling banyak
satu solusi disebut Teorema Keujudan.
1.3. KEUJUDAN DAN KETUNGGALAN SOLUSI
7
Theorem 1 : Ketunggalan
Jika f (x; y) adalah fungsi yang kontinu untuk semua titik (x; y) pada suatu
bidang segiempat
R : jx x0 j < a; jy y0 j < b;
dan terbatas di R; yaitu
jf (x; y)j 5 K
(1.3)
untuk semua (x; y) di R; maka masalah nilai awal (1.2) mempunyai paling
sedikit satu solusi y(x): Solusi ini dide…nisikan paling sedikit untuk semua x
pada selang jx x0 j < ; dengan adalah bilangan terkecil dari dua bilangan
a dan b=K:
Theorem 2 : Keujudan
Jika f (x; y) dan @f =@y adalah fungsi yang kontinu untuk semua titik (x; y)
pada suatu bidang segiempat R dan terbatas, yaitu
(a) jf j 5 K;
(b)
@f
5 M;
@y
(1.4)
untuk semua (x; y) di R; maka masalah nilai awal (1.2) mempunyai paling
banyak satu solusi y(x):
Example 10 :
Perhatikan persamaan diferensial
f (x; y) = y 0 = 1 + y 2 ; y(0) = 0:
Ambil bidang segiempat R :
sehingga
jf j = 1 + y 2 5 K = 10;
jxj < 5 dan jyj < 3: Maka a = 5 dan b = 3,
j@f =@yj = 2 jyj 5 M = 6;
= b=K = 3=10 < a:
R
dy
= dx; sehingga tan 1 y = x atau y = tan x
1 + y2
merupakan solusi dari persamaan diferensial tersebut. Karena solusinya merupakan fungsi tangen, maka solusi tersebut tidak kontinu pada x =
=2:
|
Kondisi dalam dua teorema tersebut merupakan kondisi yang cukup, bukan
perlu, dan dapat dikurangi. Sebagai contoh, dari teorema nilai rata-rata kalkulus diferensial, diperoleh
Bila y 0 = 1 + y 2 ; maka
R
f (x; y2 )
f (x; y1 ) = (y2
y1 )
@f
@y
y=e
y
dengan (x; y1 ) dan (x; y2 ) diasumsikan berada dalam R, dan ye adalah nilai yang
sesuai di antara y1 dan y2 : Dengan memperhatikan Teorema Keujudan bagian
(b) dan teorema nilai rata-rata tersebut mengakibatkan
jf (x; y2 )
f (x; y1 )j 5 M jy2
y1 j :
Kondisi yang terakhir ini, disebut sebagai kondisi Lipschitz. Meskipun kondisi Lipschitz ini lebih lemah dibandingkan dengan kondisi (b) pada Teorema
Keujudan, ia dapat menggantikan kondisi (b) tersebut. Selain itu, kekontinuan
f (x; y) tidak cukup menjamin ketunggalan solusinya. Hal ini dapat dilihat pada
contoh berikut ini.
8
CHAPTER 1. PENDAHULUAN
Example 11 : Ketaktunggalan
Masalah nilai awal
y0 =
mempunyai dua solusi, yaitu
y
1.3.1
p
jyj;
0 dan y =
y(0) = 0
x2 =4 jika x = 0
x2 =4 jika x < 0
Latihan
I. Selesaikan persamaan diferensial berikut:
1. y 0 = e
3x
2. y 0 =
sin 21 x
II. Jelaskan bahwa fungsi berikut ini merupakan solusi dari persamaan diferensial yang diberikan. Tentukan c sehingga diperoleh solusi khusus yang
memenuhi syarat awal yang diberikan.
3. y 0 + y = 1; y = ce
x
+ 1; y(0) = 2; 5
4. xy 0 = 2y; y = cx2 ; y(2) = 12
5. y 0 = y cot x; y = c sin x; y(
=2) = 2
III. Tentukan persamaan diferensial orde pertama yang terdiri dari y dan y 0 ;
yang solusinya merupakan fungsi yang diberikan berikut.
6. y = x2
7. y = tan x
Chapter 2
Persamaan Diferensial Orde
Satu
Untuk menyelesaikan atau mencari solusi dari suatu persamaan diferensial,
diperlukan metode-metode atau cara-cara yang tepat. Beragamnya bentuk persamaan diferensial membuat penyelesaian persamaan diferensial
tidak cukup dengan menggunakan satu metode saja. Metode-metode
penyelesaian persamaan diferensial tersebut antara lain adalah metode
integral langsung (sudah dipelajari di Kalkulus 3), metode pemisahan
peubah, penggunaan metode pemisahan peubah/metode transformasi, persamaan diferensial eksak, faktor pengintegral dan persamaan diferensial
linier. Diharapkan, dengan mempelajari metode-metode tersebut, mahasiswa dapat menentukan solusi dari suatu persamaan diferensial dengan
mudah, dengan hanya mengenali bentuk persamaan diferensialnya.
2.1
Metode Pemisahan Peubah
Banyak persamaan diferensial orde pertama yang dapat dituliskan dalam bentuk:
g(y)y 0 = f (x)
(2.1)
Karena y 0 =
dy
, maka persamaan (2.1) di atas dapat ditulis dalam bentuk:
dx
g(y)dy = f (x)dx:
(2.2)
Persamaan diferensial yang demikian disebut persamaan dengan peubah
terpisah. Metode penyelesaian persamaan diferensial dengan bentuk seperti
di atas disebut metode pemisahan peubah. Untuk menyelesaikan (2.1),
integralkan ke dua sisi, maka akan diperoleh
Z
Z
dy
g(y) dx = f (x)dx+c
dx
Karena (
dy
)dx = dy; maka didapatkan
dx
Z
Z
g(y)dy= f (x)dx + c
(2.3)
Jika diasumsikan bahwa f dan g adalah fungsi yang kontinu, maka integral (2.3)
ada dan dengan mengevaluasi integral ini, akan diperoleh solusi umum dari (2.1)
9
10
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Example 12 :
Carilah solusi umum persamaan diferensial berikut ini: 4yy 0 + x = 0:
Jawab :
Dengan memisahkan peubah-peubahnya, diperoleh 4ydy =
integralkan ke dua sisinya, diperoleh solusi umum
2y 2 =
xdx: Dengan meng-
x2
1 2
x + c atau
+ 2y 2 = c atau x2 + 4y 2 = c
2
2
dengan c = 2c . Solusi tersebut merupakan keluarga elips.
|
Example 13 :
Carilah solusi umum persamaan diferensial berikut: y 0 = 1 + y 2 .
Jawab :
Dengan memisahkan peubahnya dan mengintegralkannya, diperoleh:
Z
Z
dy
=
dx maka arctan y = x + c:
1+y 2
Jadi solusi umumnya adalah y = tan(x + c):
|
Example 14 :
Selesaikan masalah nilai awal berikut:
2y 0 + 4x3 y 2 = 0 ; dengan y(0) = 1:
Jawab :
Dengan memisahkan peubahnya yang sesuai dan mengintegralkannya, diperoleh:
Z
Z
2dy
2
2
=
4x3 dx; maka
= x4 + c; atau y = 4
:
2
y
y
x
c
Dengan memasukkan nilai awalnya diperoleh
y(0) =
2
= 1; sehingga c =
c
Jadi solusi masalah nilai awalnya: y(x) = (x4 + 2)
1
2:
:
|
Example 15 :
Selesaikan masalah nilai awal berikut: y 0 = 2x=y; dengan
y(2) = 4:
Jawab :
Dengan memisahkan peubahnya dan mengintegralkannya, diperoleh hasil:
Z
Z
ydy =
2xdx
1 2
y
2
= x2 + c:
Dengan memasukkan syarat awal y(2) = 4; diperoleh: 21 :(42 ) = (22 ) + c ,
sehingga c = 4. Jadi solusi masalah nilai awalnya adalah y 2 2x2 = 2c =
8.
|
2.2. METODE TRANSFORMASI
2.1.1
11
Latihan
I. Tentukan solusi umum persamaan diferensial berikut. Periksa jawabanmu
dengan menggunakan substitusi.
1. y 0 = 3(y + 1)
2. y 0 sin 2x = y cos 2x
3. y 0 = e2x cos2 y
p
4. y 0 = 1 y 2
II. Selesaikan masalah nilai awal berikut.
5. yy 0 + x = 0; dengan syarat awal y(0) =
2
6. sin dr = r cos d ; dengan syarat awal r( 21 ) =
2.2
0; 3
Metode Transformasi
Metode Transformasi atau penggunaan metode pemisahan peubah adalah suatu metode penyelesaian persamaan diferensial dengan menggunakan metode
pemisahan peubah. Perhatikan persamaan diferensial berikut:
y
(2.4)
x
dengan g adalah fungsi dari y=x. Persamaan diferensial tersebut dapat diubah
bentuknya sehingga penyelesaiannya ditentukan dengan menggunakan metoda
pemisahan peubah.
Tuliskan y=x = u atau y = xu . Turunannya adalah y 0 = u + xu0 , dengan u0 =
du
.
dx
Dari persamaan (2.4),
y0 = g
g
y
= g(u) maka y 0 = g(u) atau u + xu0 = g(u):
x
Dengan memisahkan peubah u dan x, akan diperoleh persamaan:
dx
du
=
g(u) u
x
yang dapat diselesaikan dengan menggunakan metoda pemisahan peubah.
Example 16 :
Dengan menggunakan metode transformasi, selesaikan persamaan diferensial
berikut:
2xyy 0 y 2 + x2 = 0:
Jawab :
Dengan membagi persamaan diferensial di atas dengan x2 , diperoleh:
y
2 y0
x
Dengan transformasi
y
x
2
+1=0
y
= u; persamaan di atas berubah menjadi
x
2u(u + xu0 )
u2 + 1 = 0 atau 2xuu0 + u2 + 1 = 0:
12
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Dengan memisahkan peubahnya, diperoleh persamaan:
2udu
=
1+u2
dx
x
Dengan mengintegralkannya, diperoleh hasil
ln(1 + u2 ) =
ln jxj + c atau 1 + u2 =
c
:
x
y
Dengan mengganti u = , diperoleh keluarga lingkaran-lingkaran dengan perx
samaan:
x2 + y 2 = cx atau
x
c
2
2
+ y2 =
c2
:
4
Example 17 :
Selesaikan masalah nilai awal berikut:
y0 =
p
y
2x3 cos x2
+
; dengan y( ) = 0:
x
y
|
2.2. METODE TRANSFORMASI
13
Jawab :
Transformasikan y=x = u, sehingga diperoleh y = xu dan y 0 = xu0 + u. Persamaan di atas berubah menjadi
xu0 + u = u +
2x2 cos x2
u
Dengan penghitungan aljabar yang sederhana, diperoleh persamaan
uu0 = 2x cos x2 :
Dengan pengintegralan, diperoleh 12 u2 = sin x2 + c.
p
Karena u = y=x, maka y = ux = x 2 sin x2 + 2c. Karena sin
syarat awalnya menghasilkan c = 0.
Jadi solusi dari masalah nilai awal tersebut di atas adalah :
p
|
y(x) = x 2 sin x2 :
= 0 , maka
Example 18 :
Carilah solusi umum persamaan diferensial berikut: (2x 4y+5)y 0 +x 2y+3 = 0
.
Jawab :
Transformasikan v = x 2y, sehingga y = 21 (x v) dan y 0 = 21 (1 v 0 ) : Substitusikan ke dalam persamaan di atas, sehingga diperoleh persamaan diferensial
yang baru:
(2v + 5)v 0 = 4v + 11:
Dengan menggunakan metode pemisahan peubah, diperoleh:
1
Karena v = x
1
4v+11
dv = 2dx dan v
2y, maka solusi umumnya dapat ditulis sebagai :
4x + 8y + ln j4x
2.2.1
1
ln j4v + 11j = 2x + c :
4
8y + 11j = c:
|
Latihan
I. Tentukan solusi umum dari persamaan diferensial berikut:
1. xy 0 = x + y
2. x2 y 0 = y 2 + xy + x2
3. y 0 =
y+x
.
y x
II. Selesaikan masalah nilai awal berikut:
4. xy 0 = x + y; dengan y(1) =
5. yy 0 = x3 + y 2 =x; dengan
7; 4
y(2) = 6
III. Tentukan solusi umumnya (gunakan transformasi yang diberikan):
7. y 0 = (y + x)2 ;
(y + x = v).
8. 2x2 yy 0 = tan(x2 y 2 )
2xy 2 ;
(x2 y 2 = z).
14
2.3
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Persamaan Diferensial Eksak
Misalkan u(x; y) adalah fungsi dari peubah x dan y yang terde…nisi pada D, sehingga u mempunyai turunan parsial pertama yang kontinu pada daerah de…nisinya.
Diferensial total atau eksaknya adalah:
du(x; y) =
@u(x; y)
@u(x; y)
dx +
dy; untuk semua (x; y) 2 D:
@x
@y
Suatu persamaan diferensial orde pertama yang berbentuk:
M (x; y)dx + N (x; y)dy = 0:
(2.5)
disebut eksak, jika sisi sebelah kanannya adalah diferensial total atau eksak
dari fungsi u(x; y), yaitu:
M (x; y)dx + N (x; y)dy =
@u
@u
dx +
dy;
@x
@y
(2.6)
sehingga persamaan diferensial (2.5) dapat dituliskan sebagai du = 0. Dengan
pengintegralan, diperoleh penyelesaian dari persamaan (2.5) dalam bentuk
u(x; y) = c:
(2.7)
Dengan membandingkan komponen-komponen dari persamaan (2.6), dapat
disimpulkan bahwa persamaan (2.5) adalah eksak jika ada suatu fungsi u(x; y)
= c sedemikian sehingga
(a):
@u
@u
= M; (b):
=N
@x
@y
(2.8)
Misalkan M dan N terde…nisi dan mempunyai turunan parsial pertama yang
kontinu pada bidang xy, maka dari (2.8) diperoleh:
@M
@
=
@y
@y
@u
@x
=
@2u
;
@y@x
dan
@N
@
=
@x
@x
@u
@y
=
@2u
@x@y
Dari asumsi kekontinuan, turunan keduanya adalah sama, sehingga
@M
@N
=
@y
@x
(2.9)
Kondisi ini tidak hanya perlu tetapi juga cukup bagi M dx + N dy untuk
menjadi persamaan diferensial eksak. Jika (2.5) eksak, fungsi u(x; y) dapat
ditentukan dengan menggunakan cara yang sistematik. Dari (2.8) (a), dengan
pengintegralan terhadap x, diperoleh
Z
u = M dx + k(y)
(2.10)
dengan y dipandang sebagai suatu konstanta dan k(y) berlaku sebagai konstanta integrasi. Untuk menentukan k(y), persamaan (2.10) diturunkan terhadap y; yaitu @u=@y; dan gunakan (2.8) (b) untuk mendapatkan dk=dy , kemudian integralkan dk=dy untuk mendapatkan k(y).
Rumus yang (2.10) diperoleh dari (2.8) (a). Selain itu, kita dapat menggunakan
rumus (2.8) (b) untuk mendapatkan rumus berikut :
Z
u = N dy + l(x):
(2.11)
Untuk mendapatkan l(x), turunkan @u=@y dari (2.11), gunakan (2.8) (a) untuk
mendapatkan dl=dx dan integralkan.
2.3. PERSAMAAN DIFERENSIAL EKSAK
15
Example 19 :
Perhatikan persamaan diferensial:
(3x + 2y) dx + (2x + y) dy = 0
(2.12)
Selidiki apakah persamaan diferensial tersebut eksak. Bila ya, carilah solusinya.
Jawab :
Tahap pertama: menguji keeksakan persamaan diferensial tersebut.
Misalkan M = 3x + 2y dan N = 2x + y: Maka
@M
@N
= 2 dan
= 2: Karena
@y
@x
@N
@M
=
; maka persamaan diferensial tersebut eksak.
@y
@x
Tahap ke-dua: mencari solusi persamaan diferensial.
u(x; y)
=
=
Z
Z
M dx + k(y)
(3x + 2y)dx + k(y) =
(2.13)
3x2
+ 2xy + k(y):
2
Untuk mencari k(y); turunkan u terhadap y dan gunakan rumus (2.8) (b), sehingga diperoleh:
@u
dk
= 2x +
= N = 2x + y;
@y
dy
sehingga
dk
1
= y ) k(y) = y 2 :
dy
2
Jadi solusi persamaan diferensial eksak (2.12)tersebut adalah
u(x; y) =
3x2
1
+ 2xy + y 2 = c atau 3x2 + 4xy + y 2 = c ;
2
2
(2.14)
dengan c = 2c:
Tahap ketiga: adalah pengecekan.
Perhatikan bahwa metode di atas memberikan solusi dalam bentuk implisit,
yaitu u(x; y) = c = konstanta; bukan dalam bentuk eksplisit, yaitu y = f (x):
Untuk pengecekan, kita dapat menurunkan u(x; y) = c secara implisit dan melihat apakah hal ini akan menunjukkan bahwa dy=dx = M=N atau M dx +
N dy = 0: Dalam kasus ini, dengan menurunkan u secara implisit terhadap x;
diperoleh
6x + 4y + 4xy 0 + 2yy 0 = 0 atau 3x + 2y + (2x + y)y 0 = 0:
Dengan M dan N seperti tersebut di atas, diperoleh M + N y 0 = 0; sehingga
M dx + N dy = 0: Jadi solusi benar.
|
Example 20 : Masalah nilai awal
Selesaikan masalah nilai awal berikut:
(sin x cosh y)dx
(cos x sinh y)dy = 0; y(0) = 0:
(2.15)
16
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Jawab :
I. Periksa dulu apakah persamaan tersebut eksak.
M = sin x cosh y dan N = cos x sinh y; sehingga
@M
@N
= sin x sinh y dan
= sin x sinh y:
@y
@x
@M
@N
Karena
=
; maka persamaan diferensial di atas eksak.
@y
@x
II. Dari persamaan (2.10) diperoleh:
Z
Z
u(x; y) =
M dx + k(y) = sin x cosh ydx + k(y)
=
cos x cosh y + k(y):
@u
dk
= cos x sinh y +
= N = cos x sinh y:
@y
dy
Karena dk=dy = 0; maka k = konstanta.
Jadi solusi umumnya adalah u = konstanta atau cos x cosh y = c:
Dari syarat awalnya diperoleh cos 0 cosh 0 = 1 = c:
Jadi solusi masalah nilai awalnya adalah
cos x cosh y =
1 atau cos x cosh y = 1:
III. Untuk pengecekan, (cos x cosh y)0 =
atau
sin x cosh y + cos x(sinh y)y 0 = 0;
( sin x cosh y)dx + (cos x sinh y)dy = 0; seperti pada persamaan (2.15) di atas.
Juga cos 0 cosh 0 = 1 menunjukkan bahwa jawaban memenuhi syarat awal.
|
Example 21 :
Perhatikan persamaan ydx xdy = 0: Kita lihat bahwa M = y , N = x; dan
@M=@y = 1 tetapi @N=@x = 1; sehingga persamaan diferensial tersebut tidak
eksak. Dalam kasus seperti ini, metode yang ada tidak dapat diterapkan pada
persamaan diferensial di atas. Dari (2.10) diperoleh:
Z
@u
dk
u(x; y) = M dx + k(y) = xy + k(y) dan
=x+
6= N = x:
@y
dy
@u
dk
Seharusnya
= N; sehingga bila ini terjadi diperoleh
= 2x: Namun hal
@y
dy
ini tidak mungkin, karena k(y) hanya bergantung kepada y:
|
2.3.1
Latihan
I. Perhatikan fungsi u(x; y) berikut. Tentukan persamaan diferensial eksaknya
sehingga diperoleh du = 0:
1. x2 + y 2 = c
2. u = (y
x + 1)2 :
II. Perhatikan persamaan diferensial berikut. Selidiki apakah persamaan diferensial tersebut merupakan persamaan diferensial eksak. Bila ya, carilah
solusinya. Bila tidak, jelaskan alasanmu.
3. y dx + x dy = 0
4. (2x + ey )dx + xey dy = 0:
2.4. FAKTOR PENGINTEGRAL
17
III. Selidiki apakah persamaan berikut eksak. Bila ya, selesaikan masalah nilai
awalnya. Bila tidak, jelaskan alasanmu.
5. (y
1)dx + (x
6. sinh xdx + y
1
3)dy = 0;
y(0) = 2=3:
cosh xdy = 0; y(0) = :
IV. Perhatikan persamaan diferensial berikut. Carilah solusi persamaan diferensial tersebut:
a. dengan menggunakan metoda persamaan diferensial eksak.
b. dengan metoda pemisahan peubah.
7. 2xdx + x
8. 3x
2.4
4
2
(xdy
ydx = x
3
ydx) = 0:
dy:
Faktor Pengintegral
Ide dari metoda ini sangatlah sederhana. Ada suatu persamaan diferensial yang
tidak eksak dan berbentuk:
P (x; y)dx + Q(x; y)dy = 0:
(2.16)
Bila persamaan tersebut dikalikan dengan suatu fungsi F (x; y) yang tidak nol,
maka persamaan (2.16) menjadi persamaan diferensial eksak, yaitu:
F P dx + F Qdy = 0;
(2.17)
sehingga persamaan tersebut dapat diselesaikan dengan metoda persamaan diferensial eksak. Fungsi F (x; y) ini disebut dengan faktor pengintegral (integrating factors) dari (2.16).
Example 22 :
Tunjukkan bahwa persamaan diferensial berikut:
ydx
xdy = 0
(2.18)
tidak eksak, tetapi mempunyai faktor pengintegral, sebut saja F = 1=x2 ; dan
tentukan persamaan barunya.
18
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Jawab :
Dari bentuk persamaan (2.16) diperoleh P = y dan Q = x: Karena @P=@y = 1;
tetapi @Q=@x = 1; maka persamaan diferensial di atas tidak eksak. Kalikan
persamaan (2.18) dengan F = 1=x2 ; sehingga diperoleh:
F P dx + F Qdy =
ydx
xdy
x2
= 0:
(2.19)
Misalkan F P = M = y=x2 ; maka @M=@y = 1=x2 dan F Q = N = 1=x; maka
@N=@x = 1=x2 ; sehingga persamaan (2.19) eksak. Untuk mencari solusi dari
persamaan (2.19) di atas,
ydx
xdy
x2
=
xdy
ydx
=
x2
d
y
= 0:
x
Jadi solusinya adalah y=x = c; yang merupakan persamaan garis lurus y = cx
yang melalui titik asal (0,0)
.|
Faktor pengintegral lain untuk persamaan diferensial di atas adalah : 1=y 2 ; 1=xy
dan 1=(x2 + y 2 ): Dengan memeriksa faktor pengintegral tersebut satu-persatu,
akan diketahui apakah faktor pengintegral tersebut benar-benar membuat persamaan diferensial tersebut menjadi eksak.
I. Yang pertama, bila F = 1=y 2 ; maka
F P dx + F Qdy =
ydx
xdy
y2
=d
x
y
= 0:
(2.20)
Misalkan F P = M = y=y 2 = 1=y; maka @M=@y = 1=y 2 dan F Q = N =
x=y 2 ; maka @N=@x = 1=y 2 ; sehingga persamaan (??) adalah eksak
dan solusinya adalah x=y = c atau y = x=c:
|
II. Yang ke dua, bila F = 1=xy; maka
F P dx + F Qdy =
ydx
xdy
xy
= 0:
(2.21)
Misalkan F P = M = y=xy = 1=x; maka @M=@y = 0 dan F Q = N = x=xy =
1=y; maka @N=@x = 0; sehingga persamaan (2.21) eksak. Untuk mencari
solusi dari persamaan (2.21) di atas,
ydx
xdy
xy
=
=
y
x
ydx
xdy
y2
1
x
x
d
= d ln
x
y
y
= 0:
y
sehingga solusinya adalah ln(x=y) = c atau y = x=ec = x=c :
|
III. Dan yang ke tiga, apabila F = 1=(x2 + y 2 ); maka
F P dx + F Qdy =
ydx xdy
= 0:
x2 + y 2
(2.22)
Misalkan F P = M = y=(x2 + y 2 ); maka @M=@y = (x2 y 2 )=(x2 + y 2 )2 dan
F Q = N = x=(x2 + y 2 ); maka @N=@x = (x2 y 2 )=(x2 + y 2 )2 ; sehingga
persamaan (2.22) eksak. Untuk mencari solusi dari persamaan (2.22) di atas,
2.4. FAKTOR PENGINTEGRAL
ydx xdy
x2 + y 2
=
19
xdy ydx
=
x2 + y 2
1
=
1+
y
x
ydx
x2 1 +
y
=
x
:d
y 2
x
sehingga solusinya adalah arctan
xdy
y2
x2
=
d(arctan
1
1+
y2
x2
:
xdy
ydx
x2
y
) = 0;
x
= c atau y = x tan c:
|
Example 23 :
Diketahui bahwa fungsi F (x) = x3 adalah suatu faktor pengintegral. Selidiki apakah fungsi tersebut merupakan faktor pengintegral dari persamaan:
2 sin(y 2 )dx + xy cos(y 2 )dy = 0: Jelaskan pendapatmu dan tentukan solusinya!
Jawab :
Dengan mengalikan faktor pengintegral di atas dengan persamaan diferensial
yang diketahui, maka persamaan yang baru akan berbentuk:
2x3 sin(y 2 )dx + x4 y cos(y 2 )dy = 0:
Persamaan tersebut menjadi eksak karena
@
@
2x3 sin(y 2 ) = 4x3 y cos(y 2 ) =
x4 y cos(y 2 ) :
@y
@x
Dengan menggunakan metoda persamaan diferensial eksak, akan kita cari solusi
dari persamaan diferensial di atas, yaitu:
Z
u(x; y) =
M dx + k(y)
Z
1
=
2x3 sin(y 2 )dx + k(y) = x4 sin(y 2 ) + k(y):
2
Apabila diturunkan terhadap y akan diperoleh:
@u
dk
= x4 cos(y 2 ) +
= N = x4 y cos(y 2 );
@y
dy
sehingga dk=dy = 0 dan k(y) = c1 :
Jadi solusinya adalah u(x; y) = 21 x4 sin(y 2 ) + c1 atau x4 sin(y 2 ) = c:
2.4.1
|
Menentukan faktor pengintegral
Pada awalnya, penentuan faktor pengintegral dilakukan dengan dikira-kira berdasarkan
pengalaman dan kemudian diuji. Idenya adalah persamaan (2.17), yaitu M dx+
N dy = 0 dengan M = F P dan N = F Q, yang merupakan persamaan diferensial
eksak menurut de…nisi faktor pengintegral. Oleh sebab itu kriteria ke’eksak’an
@M
@N
dari
=
pada sub bab 2.3. menjadi:
@y
@x
@
@
(F P ) =
(F Q);
(2.23)
@y
@x
yaitu Fy P + F Py = Fx Q + F Qx ; dengan x dan y menunjukkan turunan parsialnya. Mencari faktor pengintegral yang bergantung pada dua peubah x dan y
akan sangat kompleks pengerjaannya. Oleh sebab itu, fokus pembahasan hanya
20
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
pada pencarian faktor pengintegral yang bergantung pada satu peubah saja,
yaitu x saja atau y saja.
Misalkan faktor pengintegral F = F (x); maka Fy = 0 dan Fx = F 0 = dF=dx;
sehingga persamaan (2.23) menjadi F Py = F 0 Q + F Qx : Apabila persamaan di
atas dibagi dengan F Q dan diuraikan, maka persamaannya menjadi:
1 dF
1
=
F dx
Q
@P
@y
@Q
@x
:
(2.24)
Theorem 3 : Faktor Pengintegral F (x)
Jika persamaan (2.16) adalah sedemikian sehingga sisi sebelah kanan dari persamaan (2.24) bergantung hanya pada x; sebut saja R(x); maka persamaan
(2.16) mempunyai faktor pengintegral F = F (x); yang diperoleh dengan mengintegralkan (2.24) dan mencari eksponennya, yaitu:
Z
F (x) = exp R(x)dx:
(2.25)
Keterangan:
Misalkan R(x) =
1
Q
@Q
@x
@P
@y
Z
; maka
1
dF
F
=
ln jF (x)j =
Z
R(x)dx
Z
R(x)dx
Z
exp [ln jF (x)j] = exp
R(x)dx
Z
F (x) = exp R(x)dx:
Misalkan faktor pengintegral F = F (y); maka Fx = 0 dan Fy = F 0 = dF=dy;
sehingga persamaan (2.23) menjadi Fy P + F Py = F Qx : Bagi dengan F P dan
diuraikan, maka hasilnya adalah persamaan:
1 dF
1
=
F dy
P
@Q
@x
@P
@y
:
(2.26)
Theorem 4 : Faktor Pengintegral F (y)
Jika persamaan (2.16) adalah sedemikian sehinga sisi sebelah kanan dari per~
samaan (2.26) hanya bergantung pada y; sebut saja R(y);
maka persamaan
(2.16) mempunyai faktor pengintegral F = F (y); yang diperoleh dari persamaan
(2.26) dalam bentuk:
Z
F (y) = exp
~
R(y)dy:
(2.27)
Example 24 : Faktor pengintegral F (x)
Tentukan faktor pengintegral untuk contoh 2 di atas dengan menggunakan Teorema 1, yaitu soal:
2 sin(y 2 )dx + xy cos(y 2 )dy = 0:
Jawab :
2.4. FAKTOR PENGINTEGRAL
21
Karena P = 2 sin(y 2 ) dan Q = xy cos(y 2 ); maka sisi sebelah kanan dari persamaan (2.24) adalah:
R(x)
1
Q
@P
@Q
@y
@x
1
4y cos(y 2 )
xy cos(y 2 )
=
=
y cos(y 2 ) =
3
:
x
R
Jadi faktor pengintegralnya adalah F (x) = exp (3=x)dx = exp(ln x3 ) = x3 ;
seperti pada contoh.
|
Example 25 : Aplikasi Teorema 1 dan 2
Selesaikan masalah nilai awal:
2xydx + (4y + 3x2 )dy = 0; dengan y(0; 2) =
1; 5:
Jawab :
Dari persamaan di atas diketahui bahwa P = 2xy dan Q = 4y + 3x2 : Karena
@P=@y = 2x dan @Q=@x = 6x; maka persamaan di atas tidak eksak.
R(x) =
1
Q
@P
@y
@Q
@x
=
1
(2x
4y + 3x2
6x) =
4x
4y + 3x2
bergantung pada x dan y; sehingga persamaan di atas tidak mempunyai faktor
pengintegral F (x): Sedangkan
1
~
R(y)
=
P
@Q
@x
@P
@y
=
1
(6x
2xy
2x) =
2
y
sehingga faktor pengintegralnya adalah
Z
2
dy = exp(2 ln jyj) = exp[ln(y 2 )] = y 2 :
F (y) = exp
y
Kalikan persamaan diferensial pada soal di atas dengan y 2 ; sehingga persamaannya menjadi persamaan yang eksak, yaitu:
2xy 3 dx + (4y 3 + 3x2 y 2 )dy = 0:
Dengan menggunakan cara pada sub bab 2.3 mengenai persamaan diferensial
eksak, akan diperoleh solusi umumnya, yaitu: y 4 + x2 y 3 = c: Apabila kita
masukkan syarat awalnya, maka akan didapatkan hasil y 4 + x2 y 3 = 4; 93:
Jadi solusi masalah nilai awalnya adalah y 4 + x2 y 3 = 4; 93:
|
2.4.2
Latihan
I. Selidiki apakah fungsi F berikut ini merupakan faktor pengintegral dari persamaan diferensial yang diketahui. Bila ya, selesaikan masalah nilai awalnya.
1. 2ydx + xdy = 0;
y(0; 5) = 8; dan F = x:
2. (1 + xy)dx + x2 dy = 0;
3. (2x
1
y
3)dx + (3
2y
y(1) = 0; dan F = exy :
1
x)dy = 0;
y(1) =
1; dan F = x2 y 2 :
II. Perhatikan persamaan diferensial di bawah ini. Tentukan faktor pengintegral dari masing-masing persamaan diferensial tersebut dan carilah solusinya (gunakan Teorema 1 dan 2).
4. 2 cos ydx =
sin ydy:
5. (2y + xy)dx + 2xdy = 0:
6. (1 + 2x2 + 4xy)dx + 2dy = 0
22
2.5
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Persamaan Diferensial Linier
Suatu persamaan diferensial orde pertama dikatakan linier jika dapat dituliskan
sebagai:
y 0 + p(x)y = r(x);
(2.28)
dengan p dan r adalah fungsi-fungsi dari x yang diketahui. Bila r(x) 0; maka
persamaan (2.28) di atas disebut homogen, sebaliknya bila r(x) 6= 0 disebut
nonhomogen.
Untuk mencari solusi umum dari persamaan (2.28) pada suatu interval I; asumsikan bahwa p dan r kontinu di I: Untuk persamaan homogen,
y 0 + p(x)y = 0:
(2.29)
Dengan memisahkan peubahnya, diperoleh
dy
=
y
p(x)dx; sehingga ln jyj =
Z
p(x)dx + c ;
dan dengan mengambil eksponennya pada ke dua sisi persamaan di atas diperoleh:
R
y(x) = ce p(x)dx ;
(2.30)
dengan c = ec : Tanda (+) dipakai bila y(x) > 0 dan tanda ( ) bila y(x) < 0;
sedangkan c > 0 selalu. Jika c = 0; maka diperoleh solusi y(x) = 0 yang disebut
dengan solusi trivial.
Beralih kepada penyelesaian persamaan nonhomogen. Persamaan (2.28) di atas
dapat dituliskan dalam bentuk:
(py
r)dx + dy = 0:
Persamaan tersebut berbentuk P dx + Qdy = 0; dengan P = py
sehingga persamaan (2.24) pada sub bab 2.4, yaitu:
1 dF
1
=
F dx
Q
@P
@y
@Q
@x
menjadi
r dan Q = 1,
1 dF
= p(x):
F dx
Karena persamaan tersebut hanya bergantung pada x, maka persamaan (2.28)
di atas mempunyai faktor pengintegral F (x) yang diperoleh secara langsung
dengan pengintegralan dan eksponensiasi, yaitu:
R
F (x) = e
pdx
:
Kalikan persamaan (2.28) di atas dengan faktor pengintegral F (x) tersebut
sehingga persamaan (2.28) menjadi:
R
e
pdx
R
(y 0 + py) = (e
pdx
R
y)0 = e
pdx
r:
Dengan mengintegralkannya terhadap x, persamaan di atas menjadi:
Z R
R
e pdx y = e pdx rdx + c;
sehingga solusi umum untuk persamaan (2.28) di atas adalah:
Z
Z
y(x) = e h
eh rdx + c ; dimana h = p(x)dx:
Example 26 :
Selesaikan masalah nilai awal: y 0
y = e2x , y(0) = 1.
(2.31)
2.5. PERSAMAAN DIFERENSIAL LINIER
23
Jawab :
R
Diketahui p = 1; r = e2x dan h = pdx = x. Dari persamaan (2.31)
didapatkan solusi umumnya:
Z
x
e x e2x dx + c = ex [ex + c] = cex + e2x
y(x) = e
Cara lainnya, kalikan persamaan pada soal dengan eh = e
(y 0
y)e
x
= (ye
x 0
) = e2x e
x
x
, sehingga
= ex
Dengan mengintegralkan ke dua sisinya, diperoleh : ye x = ex + c atau y(x) =
e2x +cex :Dengan memasukkan syarat awal y(0) = 1; diperoleh y(0) = e0 +ce0 =
1 + c = 1; sehingga c = 0:
Jadi solusi masalah nilai awalnya adalah y(x) = e2x :
|
Example 27 :
Selesaikan y 0 + 2y = ex (3 sin 2x + 2 cos 2x) .
Jawab :
Diketahui p = 2, dan h = 2x, sehingga dari persamaan (2.31) diperoleh:
Z
y = e 2x
e2x ex (3 sin 2x + 2 cos 2x)dx + c
Z
Z
= e 2x
3e3x sin 2xdx + 2e3x cos 2xdx + c ( )
Z
Z
= e 2x e3x sin 2x
2e3x cos 2xdx + 2e3x cos 2xdx + c
2x
= e
= ce
2x
Keterangan
(*):
R
Ingat:
udv = uv
Misalkan u = sin 2x;
e3x sin 2x + c
+ ex sin 2x:
|
R
vdu:
du = 2 cos 2x dx dan dv = 3e3x dx; v = e3x , maka
Z
Z
3x
3x
3e sin 2xdx = e sin 2x
2e3x cos 2xdx
Example 28 :
Selesaikan masalah nilai awal berikut:
y 0 + y tan x = sin 2x;
y(0) = 1
Jawab :
R
R
Diketahui p = tan x, r = sin 2x = 2 sin x cos x, dan pdx = tan xdx =
ln jsec xj ; sehingga eh = sec x; e h = cos x; dan eh :r = (sec x)(2 sin x cos x) =
2 sin x: Jadi solusi umum dari persamaan di atas adalah:
Z
y(x) = cos x 2 sin xdx + c = c cos x 2 cos2 x:
Dengan memasukkan syarat awalnya, diperoleh: 1 = c:1
Jadi solusi masalah nilai awal tersebut adalah:
y(x) = 3 cos x
2 cos2 x:
|
2:1, sehingga c = 3 .
24
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Reduksi ke bentuk linier. Persamaan Bernoulli.
Persamaan diferensial nonlinier tertentu dapat diubah bentuknya ke dalam bentuk linier. Yang paling populer adalah Persamaan Bernoulli, yaitu:
y 0 + p(x)y = g(x)y a
(2.32)
dengan a bilangan real. Jika a = 0 atau a = 1, maka persamaan (2.32) adalah
persamaan diferensial linier. Sebaliknya, bila tidak maka disebut nonlinier.
1 a
Tulis u(x) = [y(x)]
. Dengan menurunkan dan mensubstitusikan y 0 dari
persamaan (2.32), diperoleh:
u0
Karena y 1
a
= (1
= (1
a)y a y 0 = (1 a)y
a)(g py 1 a ):
a
(gy a
py)
= u , maka akan diperoleh persamaan linier:
u0 + (1
a)pu = (1
a)g
(2.33)
Example 29 :
Persamaan Bernoulli. Persamaan Verhulst.
Model Populasi Logistik.
Selesaikan persamaan Bernoulli spesial, yang dinamakan dengan persamaan
Verhulst, berikut ini:
y0
dengan A dan B konstanta positif.
Ay =
By 2
(2.34)
2.6. APLIKASI PERSAMAAN DIFERENSIAL ORDE SATU
25
Jawab :
Diketahui a = 2, sehingga u = y 1 . Dengan menurunkan dan mensubstitusikan
y 0 dari persamaan (2.34), diperoleh:
u0 = y 2 y 0 = y 2 ( By 2 + Ay) = B Ay 1 ; sehingga u0 + Ay 1 = B:
Karena y 1 = u, maka u0 + Au = B: Dari persamaan (2.31), dengan p = A;
maka h = Ax dan r = B, sehingga diperoleh:
Z
B
B Ax
Ax
e + c = ce Ax + :
u=e
BeAx dx + c = e Ax
A
A
Jadi solusi umum dari persamaan (3.34) adalah:
y=
1
1
=
u
(B=A) + ce
Ax
:
|
(2.35)
Persamaan (2.35) tersebut di atas disebut hukum logistik dari pertumbuhan populasi, dengan x menyatakan waktu. Bila B = 0, maka akan memberikan pertumbuhan secara eksponensial: y = (1=c)eAx (hukum Malthus).
2.5.1
Latihan
I. Tentukan solusi umum dari persamaan diferensial berikut:
1. y 0
4y = 0; 8
2. y 0 + 2y = 6ex
3. y 0 + 3y = e
3x
II. Selesaikan masalah nilai awal berikut:
4. y 0 + 3y = 12 , y(0) = 6
5. y 0 + y = (x + 1)2 , y(0) = 3
6. y 0 + 2xy = 4x , y(0) = 3:
III. Ubahlah persamaan diferensial berikut ini ke dalam bentuk linier,
dan carilah solusinya:
7. y 0 + y = y 2
8. y 0 cos y + x sin y = 2x (sin y = z)
9. (ey + x)y 0 = 1
10. 3y 0 + y = (1
2.6
2.6.1
2x)y 4 :
Aplikasi Persamaan Diferensial Orde Satu
Pertumbuhan Alami dan Peluruhan (Natural Growth
and Decay)
Persamaan deferensial
dy
= kx; (k konstan)
dx
merupakan model matematika untuk fenomena alam yang luas.
(2.36)
26
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Pertumbuhan Populasi (Population Growth)
Misalkan P (t)) menyatakan banyaknya individu dalam populasi (manusia, serangga, dan bakteri), mempunyai tingkat (rate) kelahiran dan kematian yang
konstan (kelahiran/kematian per individu per satuan waktu). Selama selang
waktu yang singkat, t; kira-kira P (t) t kelahiran dan P (t) t kematian
terjadi, maka perubahan P (t) diperkirakan
P =(
)P (t) t;
(2.37)
sehingga
P
dP
= lim
= kP;
t!0
dt
t
dengan k =
:
(2.38)
Dengan metode pemisahan peubah dan pengintegralan, diperoleh rumus pertumbuhan populasi sebagai berikut:
Z
dP
=
P
Z
kdt =) ln P = kt + c
P (t) = ekt+c = Cekt
(2.39)
Karena C konstanta, maka dapat ditulis C = P (0) = P0 ; sehingga rumus (2:39)
dapat ditulis kembali sebagai
P (t) = ekt+c = P0 ekt :
(2.40)
Example 30 :
Pada bulan Maret 1987, populasi dunia telah mencapai 5 milyar dan terus
bertambah dengan rata-rata 380 ribu orang per hari. Dengan mengasumsikan
tingkat kelahiran dan kematian konstan, kapan populasi dunia akan mencapai
10 milyar?
2.6. APLIKASI PERSAMAAN DIFERENSIAL ORDE SATU
27
Jawab:
Misalkan P (t) adalah populasi dunia pada saat t, maka rumus pertumbuhan
populasi pada saat t adalah P (t) = P0 ekt ; dengan P menyatakan populasi dunia
dalam milyar dan t menyatakan waktu dalam tahun. Misalkan pengukuran
dimulai pada tahun 1987 dengan t = 0; maka P (0) = P0 = 5:
Karena P meningkat sebesar 380 ribu (= 0,00038 milyar) orang per hari pada
saat t = 0; berarti peningkatan populasi per tahun sebesar P 0 (0) = (0; 00038)(365; 25) =
0; 1388 milyar. Dari persamaan (2:40) diperoleh
P 0 (t) = P0 kekt =) untuk t = 0; P 0 (0) = P0 kek:0 = P0 k; sehingga
k=
P 0 (0)
P0
0; 1388
5
0; 0278:
Jadi pertumbuhan populasi per tahun pada 1987 kira-kira 2,78%.
Bila P (t) = 10; maka
10 = P (t) = 5e(0;0278)t =) e(0;0278)t = 2
ln(e(0;0278)t ) = ln 2 =) 0; 0278t = 0; 693
t = 24; 928
25 (tahun).
Karena tahun 1987 diketahui sebagai tahun awal t = 0; maka 25 tahun kemudian, yaitu pada tahun 2012, populasi dunia akan mencapai 10 milyar.
|
Example 31 :
Misalkan P (t) = Cekt adalah populasi dari suatu koloni bakteri pada saat
t; yang pada saat t = 0; populasinya mencapai 1000 dan bertambah dobel
banyaknya setelah 1 jam. Berapa populasi pada saat t = 90 menit?
Jawab:
Dari informasi tersebut diperoleh:
P (0) = 1000 = Ce0 = C;
dan
P (1) = 2000 = 1000ek =) k = ln 2
0; 69315:
Jadi persamaan diferensialnya menjadi
dP
= kP = (ln 2):P
dt
(0; 69315) :P;
dan rumus banyaknya populasi bakteri pada saat t adalah
P (t) = 1000e(ln 2)t
1000e(0;69315):t :
Untuk t = 90 = 1; 5 jam, banyaknya bakteri adalah
P (1; 5) = 1000e(0;69315):(1;5)
2828 bakteri.
|
28
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Peluruhan Radioaktif (Radioactive Decay )
Perhatikan sebuah sampel materi yang mengandung N (t) atom dari suatu isotop radioaktif tertentu pada waktu t: Berdasarkan penelitian, pecahan yang
konstan (a constant fraction) dari atom radioaktif ini akan luruh secara spontan, menjadi atom-atom elemen lain atau menjadi isotop lain dari elemen yang
sama, selama satuan waktu tertentu. Konsekuensinya, sampel tersebut persis
seperti populasi awalnya dengan tingkat kematian yang konstan (tidak terjadi
kelahiran). Model untuk N (t) tersebut diperoleh dengan mengganti P pada
persamaan (2:37) dengan N; dan k > 0; = 0; sehingga persamaannya menjadi
dN
=
dt
kN =)
dN
=
N
kdt
dan persamaan (2:40) menjadi
N (t) = N0 e
kt
;
(2.41)
dengan k disebut sebagai konstanta peluruhan, yang nilainya bergantung pada
isotop radioaktif partikuler.
Konstanta peluruhan k ini sering dikaitkan dengan konstanta empiris yang
lain, yaitu paruh waktu dari suatu isotop. Paruh waktu
(baca ”tau”)
adalah waktu yang diperlukan bagi suatu isotop untuk meluruh menjadi setengah bagian. Untuk mencari kaitan antara k dan ; maka tulis t =
dan
N = 21 N0 ; sehingga persamaan (2:41) menjadi
1
N0 = N0 e
2
k
dan
=
ln 2
:
k
(2.42)
Sebagai contoh, bila diketahui konstanta peluruhan k dari isotop 14 C adalah
ln 2
k = 0; 0001216; maka paruh waktu dari isotop tersebut adalah = 0;0001216
5700 tahun.
|
Example 32 :
Suatu spesimen arang kayu yang ditemukan di monumen bebatuan Stonehenge
(Inggris) ternyata mengandung 63% karbon 14 C; sebanyak sampel arang kayu
pada saat ini dengan massa yang sama. Berapakah umur sampel tersebut?
2.6. APLIKASI PERSAMAAN DIFERENSIAL ORDE SATU
29
Jawab:
Ambil t = 0 sebagai waktu matinya pohon di mana arang Stonehenge terbuat
dan N0 sebagai banyaknya atom 14 C yang dikandung arang kayu tersebut pada
awalnya. Jika diketahui N = (0; 63)N0 = N0 e kt ; maka dengan konstanta
peluruhan k = 0; 0001216; diperoleh umur sampel
t=
ln(0; 63)
0; 0001216
3800 (tahun).
Bila spesimen arang kayu tersebut ditemukan pada tahun 2000, maka diperkirakan pembangunan Stonehenge tersebut terjadi pada tahun 1800 S.M.
|
Pendinginan dan Pemanasan (Cooling and Heating)
2.6.2
Menurut hukum Newton tentang pendinginan, laju perubahan suhu T (t) dari
suatu benda yang dimasukkan (ditenggelamkan) ke dalam suatu medium dengan
suhu yang konstan A adalah sebanding dengan selisih A T; yaitu
dT
= k(A
dt
T );
(2.43)
dengan k adalah suatu konstanta positif. Persamaan ini merupakan suatu contoh dari persamaan diferensial linier orde pertama dengan koe…sien konstanta:
dx
= ax + b:
dt
Example 33 :
Seekor ayam seberat 2,5 kg yang pada awalnya bersuhu 500 F; dimasukkan ke
dalam oven yang bersuhu 3750 F pada jam 5 P.M. Setelah 75 menit, suhu ayam
menjadi 1250 F: Kapan suhu ayam akan menjadi 1500 F (medium rare)?
Jawab:
Misalkan t dalam menit dan t = 0 menyatakan jam 5 P.M. Diasumsikan suhu
ayam T (t) seragam. Diketahui A = 375; T (0) = 50 dan T (75) = 125; sehingga
diperoleh
Z
Z
dT
1
= k(375 T ) =)
dT = kdt;
dt
375 T
ln(375
375
T = Ce
kt
T ) = kt + c;
=) T = 375
Ce
Dari T (0) = 50; diperoleh C = 325; sehingga T (t) = 375
dari T (75) = 125; diperoleh
375
125 = 325e
k=
1
ln
75
75k
=) e
250
325
75k
=
kt
:
325e
kt
: Sementara
250
325
0; 0035:
Jika T (t) = 150; maka persamaannya menjadi
150 = 375
325e
(0;0035):t
= 225 =) t =
325e
(0;0035):t
1
ln
0; 0035
225
325
105 (menit) .
Jadi waktu yang diperlukan ayam agar bersuhu 1500 F adalah 105 menit dari
waktu semula jam 5 P.M. atau pada jam 6.45 P.M.
|
30
2.6.3
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Bunga Majemuk (Interest Compound)
Istilah bunga majemuk mengacu pada suatu prosedur penghitungan bunga di
mana bunga tertentu pada suatu periode ditambahkan ke dalam modal awal.
Jumlah yang baru menjadi modal baru untuk periode bunga selanjutnya. Bunga
yang diperoleh dalam periode bunga sebelumnya, menghasilkan bunga untuk
periode bunga selanjutnya.
Misalkan A(t) menyatakan banyaknya rupiah dalam rekening tabungan, pada
waktu t (tahun), dengan bunga tahunan sebesar r, dan A0 menyatakan tabungan pada saat t = 0: Pihak bank setuju akan membayar bunga pada setiap akhir
periode yang sudah disepakati. Catatan: 10% bunga tahunan berarti r = 0; 10:
Jika banyaknya periode dalam satu tahun adalah n maka dikatakan bahwa bunganya dimajemukkan n kali per tahun (contohnya: tahunan = 1, kuarteran = 4,
bulanan = 12, dst.). Jadi pada akhir periode pertama, saldonya akan menjadi
A(t) = A0 +
r
r
A0 = A0 1 +
:
n
n
Pada akhir periode ke dua, saldonya adalah
A(t) = A0 1 +
r
r
r
r
+ A0 1 +
= A0 1 +
n
n
n
n
2
:
Setelah n periode, saldonya menjadi
A(t) = A0 1 +
r
n
n
:
Jika investasi diperpanjang ke tahun berikutnya, maka saldonya akan menjadi
A(t) = A0 1 +
r
n
2n
r
n
nt
:
Untuk investasi t tahun, saldonya menjadi
A(t) = A0 1 +
nt
Karena 1 + nr = 1 +
fungsi eksponensial
r n t
n
:
; maka fungsi A dapat dituliskan dalam bentuk
A(t) = A0 bt ;
(2.44)
r n
n
dengan b = 1 +
:
Bunga yang diberikan oleh bank dikenal sebagai tingkat nominal. Jika bunga
dimajemukkan lebih sering daripada sekali setahun, jumlah yang diperoleh lebih
daripada tingkat nominal. Selain tingkat nominal, dikenal pula istilah tingkat
efektif. Tingkat efektif tahunan menginformasikan berapa banyak bunga yang
n
1:
diperoleh. Tingkat bunga efektif kuantitasnya dihitung dari 1 + nr
Bunga majemuk kontinu (continues compound interest) berarti bahwa selama
selang waktu yang singkat t, banyaknya bunga yang ditambahkan pada rekening diperkirakan A = rA(t) t; sehingga
A
dA
= lim
= rA =) A(t) = Cert
t!0
dt
t
(2.45)
dengan C suatu konstanta, yang dapat ditulis sebagai C = A(0) = A0 : Tingkat
bunga efektif tahunan dihitung dari rumus er 1:
Example 34 :
2.6. APLIKASI PERSAMAAN DIFERENSIAL ORDE SATU
31
Tentukan tingkat efektif jika uang sejumlah 1 juta rupiah ditabung dengan
tingkat bunga majemuk kontinu tahunan sebesar 5%.
Jawab:
Tingkat bunga efektifnya adalah e0;05
1
0; 05127 = 5; 127%:
|
Example 35 :
Uang sejumlah 5 juta rupiah ditabung di suatu bank yang tingkat bunga majemuk kontinu tahunannya adalah 4%.
a. Tentukan saldonya setelah 5 tahun.
b. Berapa lama uang tersebut akan menjadi dua kali lipat dari semula (dobel)?
Jawab:
Diketahui A0 = 5:000:000; r = 4% = 0; 04 dan t = 5:
a. Saldo setelah 4 tahun adalah
A(5) = 5:000:000e(0;04):5
6:107:013; 791 (rupiah):
b. Karena saldo awalnya adalah 5 juta rupiah, maka dobel saldo pada saat t
adalah 10 juta rupiah, sehingga
A(t) = 10:000:000 = 5:000:000e0;04t
0; 04t = ln 2 =) t =
2.6.4
ln 2
0; 04
17; 33 (tahun).
|
Eliminasi Obat (Drug Elimination)
Dalam banyak kasus, jumlah A(t) dari obat tertentu dalam aliran darah, yang
mengukur kelebihan level alami dari obat, akan menurun pada tingkat yang
proporsional dengan jumlah kelebihan yang ada. Yaitu,
dA
=
dt
dengan
> 0: Parameter
A;
(2.46)
disebut konstanta eliminasi dari obat.
Example 36 :
Misalkan sodium pentobarbitol digunakan untuk membius seekor anjing. Seekor
anjing dibius ketika konsentrasi aliran darahnya mengandung paling sedikit 45
miligram sodium pentobarbitol per kilogram berat anjing. Misalkan diketahui
juga bahwa sodium pentobarbitol akan berkurang secara eksponensial dari aliran darah anjing, dalam paruh waktu 5 jam. Berapa dosis sodium pentobarbitol yang direkomendasikan untuk membius anjing seberat 50 kg dalam waktu 1
jam?
Jawab:
32
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
Misalkan A(t) adalah jumlah sodium pentobarbitol dalam aliran darah. Dari
rumus (2.46) diperoleh: A(t) = A0 e t : Dari soal diketahui bahwa = t1=2 = 5
jam.
A(t)
=
5
=
=
1
A0 = A0 e t = A0 e
2
1
ln = ln 2
2
ln 2
0; 693
= 0; 1386:
5
5
5
Untuk t = 1; jumlah sodium pentobarbitol yang ada dalam darah adalah
A(1) = 50
45 = 2250mg:
Selanjutnya
A(1)
A0
= A0 e 0;1386:1 = 2250
2250
2250
=
=
2584; 72
0;1386
e
0; 8705
2585mg:
Jadi dosis sodium pentobarbitol yang direkomendasika sebesar 2585 mg.
2.6.5
|
Hukum Torricelli
Menurut hukum Torricelli, laju perubahan volume air V dalam tangki yang
airnya mengalir keluar adalah sebanding dengan akar kuadrat kedalaman air y
dalam tangki, yaitu
dV
p
= k y;
(2.47)
dt
dengan k suatu konstanta. Jika tangkinya berbentuk silinder dengan luas penampang A; maka V = Ay; dan dV =dt = A(dy=dt); sehingga
dy
1
=
dt
A
dV
dt
=)
dy
=
dt
p
h y;
(2.48)
dengan h = k=A:
Misalkan sebuah tangki air mempunyai lubang di dasarnya dengan luas penampang a; sehingga air mengalir keluar dari lubang tersebut. Nyatakan y(t) sebagai
tinggi (kedalaman) air dalam tangki pada saat t dan V (t) adalah volume air
dalam tangki. Dalam kondisi yang ideal, kecepatan air keluar melalui lubang
adalah
p
(2.49)
= 2gy
( dibaca ”upsilon”). Dengan memperhitungkan kendala (constriction) jet air
dari suatu pipa/lubang (ori…ce), maka
p
= c 2gy;
(2.50)
dengan c adalah konstanta empiris di antara 0 dan 1 (biasanya sekitar 0,6 untuk
aliran air yang kecil). Agar lebih sederhana, diambil c = 1 untuk pembahasan
berikut. Akibatnya, persamaan (2:47) menjadi
dV
=
dt
a =
p
a 2gy;
yang merupakan hukum Torricelli untuk pengosongan tangki.
(2.51)
2.6. APLIKASI PERSAMAAN DIFERENSIAL ORDE SATU
33
Jika A(y) menyatakan luas penampang tangki pada ketinggian y; maka volume
yang diperoleh dari penampang adalah
V =
Zy
A(y)dy
(2.52)
0
sehingga dari teorema kalkulus dasar diperoleh
dV
dV dy
dy
=
:
= A(y): :
dt
dy dt
dt
(2.53)
Dari persamaan (2:49) dan (2:51) diperoleh
A(y):
dy
=
dt
p
a 2gy;
(2.54)
yang merupakan bentuk alternatif dari hukum Torricelli.
Example 37 :
Sebuah tangki yang berbentuk setengah bola (hemispherical ) mempunyai jarijari atas 4 kaki (feet) dan pada saat t = 0; tangki tersebut penuh dengan air.
Pada suatu saat, sebuah lubang bundar dengan diameter 1 inci di dasar tangki
terbuka. Berapa lama waktu yang diperlukan agar semua air dalam tangki
tersebut mengalir keluar?
Jawab:
Misalkan A(y) adalah luas penampang tangki dengan jari-jari r1 = 4 kaki dan
1
a adalah luas penampang lubang dengan jari-jari r2 = 0; 5 inci = 24
kaki (1
kaki = 30 cm dan 1 inci = 2,45 cm). Dari gambar segitiga pada gra…k berikut,
dapat dilihat bahwa
A(y) = r2 =
16
(4
2
y)
=
8y
y2 :
Dengan g = 9; 8 m= det2 = 32 kaki/det2 ; persamaan (2:53) menjadi
8y
Z
y2
8y 1=2
16 3=2
y
3
dy
=
dt
1
24
y 3=2 dy =
2 5=2
y
=
5
Z
2
p
64
1
72
dt
1
t + c:
72
Karena y(0) = 4; maka c = 448=15: Agar semua air mengalir keluar dari tangki,
maka tinggi air y = 0; sehingga
1
448
t+
= 0 =) t = 72
72
15
448
15
2150 detik = 35 menit 50 detik.
Jadi kira-kira perlu waktu sekitar 36 menit untuk mengosongkan tangki air.
|
34
CHAPTER 2. PERSAMAAN DIFERENSIAL ORDE SATU
2.6.6
Latihan
1. Massa dari suatu material radioaktif dalam suatu sampel diberikan oleh
rumus
M (t) = 100e 0;0017t ; dengan t diukur dalam tahun. Tentukan paruh
waktu dari substansi radioaktif tersebut.
2. Suatu larutan yang suhunya 1000 C diletakkan di atas meja, di mana suhu
ruangan diasumsikan konstan pada suhu 200 C: Larutan menjadi dingin
dengan suhu 600 C setelah 5 menit.
(a) Carilah rumus untuk suhu larutan (T ), selama t menit, setelah diletakkan di atas meja.
(b) Tentukan waktu yang diperlukan bagi larutan tersebut untuk menjadi
dingin pada suhu 220 C:
3. Sebuah tangki air berbentuk seperti silinder tegak dengan jari-jari 3 kaki.
Awalnya tangki tersebut memuat air dengan kedalaman 9 kaki dan tutup
lubang bawah silinder yang berbentuk lingkaran dengan jari-jari 1 inchi,
dibuka pada saat t = 0: Berapa lama air dalam tangki tersebut akan habis?
4. Sesosok jenazah diketemukan pada tengah malam dan suhu badannya
840 F: Jika suhu badan pada saat meninggal 980 F; suhu ruangan konstan
pada 660 F; dan konstanta proporsionalitasnya 0,1 per jam, berapa lama
jenazah tersebut sudah meninggal, sejak pertama diketemukan?
5. Sejumlah uang ditabung di suatu bank dengan tingkat bunga majemuk
kontinu tahunan sebesar 2,85%.
(a) Tentukan saldonya setelah 3 tahun.
(b) Berapa lama waktu yang diperlukan agar uang tersebut menjadi dua
kali
lipat
banyaknya?
Chapter 3
Persamaan Diferensial
Linier Orde Ke-n
3.1
Persamaan Diferensial Linier Homogen
Persamaan diferensial biasa orde ke-n adalah suatu persamaan dengan turunan
ke-n dari suatu fungsi tak diketahui y(x); dengan y (n) = dn y=dxn adalah turunan tertinggi yang terdapat dalam persamaan tersebut. Persamaan yang
berbentuk:
F (x; y; y 0 ; :::; y (n) ) = 0;
mungkin memuat suatu turunan yang lebih rendah dari y atau y sendiri, mungkin
pula tidak. Suatu persamaan diferensial biasa orde ke-n dikatakan linier jika
dapat dituliskan sebagai:
y (n) + pn
1 (x)y
(n 1)
+ ::: + p1 (x)y 0 + p0 (x)y = r(x):
(3.1)
dimana r dan koe…sien p0 ; p1 ; :::; pn 1 adalah fungsi-fungsi dari x yang diketahui. Persamaan (3.1) dikatakan nonlinier jika tidak dapat dituliskan dalam
bentuk persamaan (3.1). Bila r(x) 0; persamaan (3.1) menjadi
y (n) + pn
1 (x)y
(n 1)
+ ::: + p1 (x)y 0 + p0 (x)y = 0:
(3.2)
dan disebut homogen. Bila r(x) 6= 0; persamaan tersebut dinamakan nonhomogen.
Untuk n = 2; bentuk liniernya dapat dituliskan sebagai berikut:
y 00 + p(x)y 0 + q(x)y = r(x)
dengan p; q;dan r adalah fungsi-fungsi dari x yang diketahui. Jika r(x)
(yaitu r(x) = 0 untuk semua x), maka persamaan (3.3) menjadi
y 00 + p(x)y 0 + q(x)y = 0
(3.3)
0
(3.4)
dan disebut homogen. Jika r(x) 6= 0, maka (3.3) disebut nonhomogen. Fungsi
p dan q pada (3.3) dan (3.4) disebut koe…sien dari persamaan.
Berikut ini adalah beberapa contoh dari persamaan diferensial orde ke dua:
1. linier nonhomogen:
2. linier homogen:
(1
y 00 + 4y = e
x2 )y 00
x
: sin x:
2xy 0 + 6y = 0:
35
36
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
3. nonlinier:
x(y 00 y + y 02 ) + 2y 0 y = 0
dan
y 00 =
p
y 02 + 1:
Solusi dari persamaan diferensial orde ke dua (linier atau nonlinier) pada selang
terbuka a < x < b adalah fungsi y = h(x) yang terde…nisi dan mempunyai
turunan y 0 = h0 (x), y 00 = h00 (x); serta memenuhi persamaan diferensial itu
untuk semua x di dalam interval tersebut. Untuk persamaan diferensial (linier
atau nonlinier) orde ke-n, solusinya pada interval terbuka I adalah fungsi y =
h(x) yang terde…nisi dan dapat diturunkan n kali pada I:
3.1.1
Prinsip Superposisi atau Kelinieran
Theorem 5 : Superposisi untuk persamaan Orde ke dua
Untuk persamaan diferensial linier homogen orde ke dua (3.4), suatu kombinasi
linier dari dua solusi pada suatu selang terbuka I juga merupakan suatu solusi
dari (3.4) pada I. Secara khusus, untuk persamaan yang seperti itu, jumlah dan
perkalian konstanta dari suatu solusi adalah juga solusi.
Bukti:
Misalkan y1 dan y2 adalah solusi dari (3.4) pada I. Akan ditunjukkan bahwa
kombinasi linier dari y1 dan y2 juga solusi dari (3.4). Misalkan kombinasi liniernya adalah y = c1 y1 + c2 y2 ; maka turunan pertama dan kedua dari y adalah
y0
y 00
=
=
(c1 y1 + c2 y2 )0 = c1 y10 + c2 y20 ;
(c1 y1 + c2 y2 )00 = c1 y100 + c2 y200 :
Selanjutnya y dan turunan-turunannya disubstitusikan ke dalam persamaan
(3.4), sehingga diperoleh:
y 00 + py 0 + qy
= (c1 y1 + c2 y2 )00 + p(c1 y1 + c2 y2 )0 + q(c1 y1 + c2 y2 )
= c1 y100 + c2 y200 + p(c1 y10 + c2 y20 ) + q(c1 y1 + c2 y2 )
= c1 (y100 + py10 + qy1 ) + c2 (y200 + py20 + qy2 )
= (c1 )(0) + (c2 )(0) = 0:
Karena y1 dan y2 solusi, maka y100 +py10 +qy1 = 0 dan y200 +py20 +qy2 = 0; sehingga
y = c1 y1 + c2 y2 juga solusi dari (3.4) pada I.
Untuk persamaan diferensial orde ke n; teorema superposisinya dapat dinyatakan dalam bentuk yang lebih umum, yaitu:
3.1. PERSAMAAN DIFERENSIAL LINIER HOMOGEN
37
Theorem 6 : Prinsip Superposisi atau Kelinieran Orde ke n
Untuk persamaan diferensial linier homogen orde ke-n (3.2), jumlah dan perkalian
konstanta dari solusinya pada interval terbuka I adalah juga solusi dari (3.2)
pada I:
Penting untuk diingat bahwa teorema di atas tidak berlaku untuk persamaan
linier nonhomogen atau persamaan nonlinier.
Example 38 :
Fungsi y = ex dan y = e x adalah solusi dari persamaan diferensial linier
homogen y 00 y = 0, untuk semua x karena bila fungsi y = ex disubstitusikan
ke dalam persamaan diferensial di atas, akan diperoleh
(ex )00
x
Demikian pula untuk y = e
(e
x 00
)
ex = ex
ex = 0:
; akan diperoleh
e
x
=e
x
e
x
= 0:
Selanjutnya apabila ex dan e x dikalikan dengan suatu konstanta yang berbeda
dan dijumlahkan, seperti misalnya y = 3ex + 8e x ; dan disubstitusikan ke
dalam persamaan diferensial di atas, maka akan diperoleh
y 00
y
= ( 3ex + 8e
= ( 3ex + 8e
x 00
)
x
)
( 3ex + 8e x )
( 3ex + 8e x ) = 0:
|
Ilustrasi di atas menyatakan bahwa untuk persamaan linier homogen, akan selalu didapatkan solusi baru dari solusi yang sudah diketahui dengan cara mengalikannya dengan suatu konstanta dan menjumlahkannya. Dari fungsi y1 (= ex )
dan y2 (= e x ); didapatkan suatu fungsi yang berbentuk:
y = c1 y1 + c2 y2
(3.5)
dengan c1 dan c2 suatu konstanta sebarang. Fungsi yang seperti itu disebut
sebagai kombinasi linier dari y1 dan y2 :
Example 39 : Persamaan diferensial linier nonhomogen
Fungsi y = 1 + cos x dan y = 1 + sin x adalah solusi dari persamaan diferensial
linier nonhomogen y 00 + y = 1: Sedangkan fungsi berikut bukan solusi dari
persamaan diferensial ini, yaitu
y = 2(1 + cos x) dan y = (1 + cos x) + (1 + sin x):
(Periksa!)
|
38
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Example 40 : Persamaan diferensial nonlinier
Dengan menggunakan substitusi, fungsi y = x2 dan y = 1 adalah solusi dari
persamaan diferensial nonlinier y 00 y xy 0 = 0: Sedangkan fungsi berikut bukan
solusi dari persamaan diferensial ini, yaitu y = x2 dan y = x2 + 1:
|
(Periksa!)
De…nition 1 : basis, proporsional
Solusi umum dari persamaan diferensial orde dua (3.4) pada selang terbuka I
adalah solusi (3.5) dengan y1 dan y2 bukan solusi proporsional dari (3.4) pada
I; dengan c1 dan c2 suatu konstanta sebarang. y1 dan y2 ini dinamakan basis
(sistem fundamental) dari (3.4) pada I: Solusi khusus dari persamaan (3.4)
pada I diperoleh jika kita mempunyai nilai yang khusus untuk c1 dan c2 pada
(3.5).
y1 dan y2 disebut proporsional pada I jika
(a) y1 = ky2 atau (b) y2 = ly1
(3.6)
untuk semua x pada I; dengan k dan l adalah suatu bilangan sebarang.
Sedangkan untuk persamaan diferensial orde ke n; solusi umumnya pada suatu
interval terbuka I adalah solusi dari (3.2) pada I yang berbentuk:
y(x) = c1 y1 (x) + ::: + cn yn (x); c1 ; :::; cn sebarang.
(3.7)
dengan y1 ; :::; yn merupakan basis (sistem fundamental) dari solusi (3.2) pada
I: Solusi khusus dari (3.2) pada I diperoleh jika n konstanta c1 ; :::; cn pada (3.7)
diganti dengan nilai-nilai tertentu.
De…nition 2 : kebebasan linier orde ke dua
Dua fungsi y1 (x) dan y2 (x) dikatakan bebas secara linier pada selang I; di mana
mereka terde…nisi, jika persamaan
k1 y1 (x) + k2 y2 (x) = 0
(3.8)
mengakibatkan k1 = 0; k2 = 0: Dikatakan tidak bebas secara linier pada I; jika
persamaan ini juga memuat konstanta k1 ; k2 yang tidak nol keduanya. Jika
k1 6= 0 atau k2 6= 0; maka
y1 =
k2
y2 atau y2 =
k1
k1
y1 :
k2
Jadi y1 dan y2 proporsional.
Basis solusi dari persamaan (3.4) pada selang I adalah pasangan y1 dan y2 yang
bebas linier pada I.
3.1. PERSAMAAN DIFERENSIAL LINIER HOMOGEN
39
De…nition 3 : (kebebasan linier untuk orde ke n)
n fungsi y1 (x); ..., yn (x) disebut bebas linier pada beberapa interval I di mana
mereka terde…nisi, jika persamaan
k1 y1 (x) + ::: + kn yn (x) = 0 pada I
(3.9)
menyebabkan semua k1; :::; kn adalah nol. Fungsi-fungsi ini disebut tidak bebas
linier pada I jika persamaan ini memuat k1 ; :::; kn yang tidak semuanya nol.
Dengan kata lain, y1 (x); ..., yn (x) tidak bebas linier pada I jika dan hanya
jika dapat dinyatakan (paling sedikit) satu dari fungsi-fungsi ini pada I sebagai
kombinasi linier dari n 1 fungsi-fungsi yang lain.
Sebagai contoh, jika persamaan (3.9) memuat k1 6= 0; maka persamaan (3.9)
dapat dibagi dengan k1 dan y1 dapat dinyatakan sebagai kombinasi linier, yaitu:
y1 =
1
(k2 y2 + ::: + kn yn ):
k1
Example 41 :
Fungsi-fungsi y1 = e2x dan y2 = e 2x membentuk basis dari persamaan diferensial y 00 4y = 0; untuk semua x; karena y1 =y2 = e4x 6= konstanta (tidak
proporsional). Jadi solusi umumnya adalah y = c1 e2x + c2 e 2x :
|
Example 42 :
Dua fungsi y1 = cos x dan y2 = sin x adalah solusi dari persamaan diferensial
y 00 + y = 0:
Cos x dan sin x adalah tidak proporsional, karena y1 =y2 = cot x 6= konstanta.
Oleh sebab itu mereka membentuk basis dari persamaan diferensial tersebut
untuk semua x dan solusi umumnya adalah y = c1 cos x + c2 sin x: |
Example 43 :
Tunjukkan bahwa fungsi-fungsi y1 = x; y2 = 3x; y3 = x2 adalah tidak bebas
linier pada suatu interval.
Jawab:
Tulis y2 = 3y1 + 0:y3 : Karena salah satu fungsi di atas dapat dinyatakan
sebagai kombinasi linier dari fungsi-fungsi yang lain, maka dapat dikatakan
bahwa fungsi-fungsi tersebut tidak bebas linier.
|
Example 44 :
Tunjukkan bahwa y1 = x; y2 = x2 dan y3 = x3 adalah bebas linier pada suatu
interval, sebagai contoh pada interval 1 6 x 6 2:
40
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Jawab:
Dari persamaan (3.9) diperoleh: k1 x + k2 x2 + k3 x3 = 0:
Dengan mengambil x = 1; 1; 2; diperoleh:
-k1 + k2 k3 = 0; k1 + k2 + k3 = 0; dan 2k1 + 4k2 + 8k3 = 0.
Akibatnya : k1 = 0; k2 = 0, dan k3 = 0 atau bebas linier.
|
3.1.2
Masalah Nilai Awal
Untuk persamaan linier homogen orde ke-dua (3.4), solusi umumnya akan berbentuk
y = c1 y1 + c2 y2
(3.10)
yaitu suatu kombinasi linier dari dua solusi yang memuat dua konstanta sebarang c1 dan c2 : Masalah nilai awalnya terdiri dari persamaan (3.4) dan dua
kondisi atau syarat awal, yaitu:
y(x0 ) = K0; dan y 0 (x0 ) = K1
(3.11)
Sedangkan untuk persamaan diferensial orde ke n; masalah nilai awalnya terdiri
dari persamaan (3.2) dan n syarat awal, yaitu:
y(x0 ) = K0 ; y 0 (x0 ) = K1 ; :::; y (n 1) (x0 ) = Kn 1 ; dengan x0 adalah titik tetap
pada interval I.
Example 45 :
Diketahui fungsi y = e3x dan y = e 3x adalah solusi dari persamaan diferensial
y 00 9y = 0; dengan syarat awal y(0) = 2; y 0 (0) = 0: Selidiki kebenaran
pernyataan tersebut dan selesaikan masalah nilai awalnya.
Jawab:
Misalkan kombinasi linier y = c1 e3x +c2 e 3x adalah solusi umum dari persamaan
diferensial yang diberikan. Turunan pertama dan kedua dari y adalah y 0 =
3c1 e3x 3c2 e 3x dan y 00 = 9c1 e3x + 9c2 e 3x : Dengan mensubstitusikan y dan
turunannya ke dalam persamaan diferensial yang diketahui diperoleh:
9c1 e3x + 9c2 e 3x 9(c1 e3x + c2 e 3x ) = 0; sehingga pernyataan bahwa y = e3x
dan y = e 3x adalah solusi dari y 00 9y = 0:adalah benar.
Dari syarat awal y(0) = 2; y 0 (0) = 0; diperoleh c1 = 1 dan c2 = 1:
Jadi solusi masalah nilai awalnya adalah y = e3x + e 3x :
|
Example 46 :
Selesaikan masalah nilai awal berikut:
y 00
y = 0; y(0) = 5; y 0 (0) = 3:
3.2. PERSAMAAN DENGAN KOEFISIEN KONSTANTA
41
Jawab:
Tahap pertama: pada contoh 1 diketahui bahwa y = ex dan y = e x adalah
solusi dari persamaan diferensial tersebut di atas sehingga solusi umumnya,
y = c1 ex + c2 e x :
Tahap kedua: karena y 0 = c1 ex c2 e x ; maka dari kondisi awalnya diketahui
bahwa y(0) = c1 + c2 = 5 dan y 0 (0) = c1 c2 = 3; sehingga diperoleh hasil
c1 = 4 dan c2 = 1:
Jadi solusi khususnya adalah y(x) = 4ex + e x :
|
3.1.3
Latihan
I. Tunjukkan bahwa fungsi-fungsi berikut membentuk basis solusi dari persamaan diferensial yang diberikan pada suatu interval tertentu.
1. 1; x2 ; x4 ; dan x2 y 000
2. ex ; e
x
3xy 00 + 3y 0 = 0:
; cos x; sin x; dan
y iv
y = 0:
II. Tunjukkan bahwa fungsi-fungsi berikut membentuk basis solusi dari masalah
nilai awal yang diberikan dan carilah solusinya.
3. ex ; xex dan y 00
2y 0 + y = 0; dengan y(0) = 4; y 0 (0) = 3:
4. ex ; e3x dan y 00
4y 0 + 3y = 0; dengan y(0) =
1; y 0 (0) =
5:
5. cos 2x; sin 2x dan y 00 + 4y = 0; dengan y(0) =
5; y 0 (0) = 2:
6. 1; x; x2 ; x3 dan y iv = 0; dengan y(0) = 0;
0; y 000 (0) = 48:
y 0 (0) = 6;
y 00 (0) =
III. Selidiki apakah fungsi berikut bebas linier pada selang tertentu.
7. x + 1; x
1 (0 < x < 1):
8. sin 2x; sin x cos x; pada suatu interval :
9. jxj x; x2 (0 < x < 1):
10. jcos xj ; cos x (0 < x < ):
11. cosh x; cosh 2x; pada suatu interval.
12. 1; x; x2
13. sin x; sin 2x; sin 3x:
3.2
3.2.1
Persamaan dengan Koe…sien Konstanta
Persaman diferensial linier homogen orde ke-dua
Perhatikan persamaan linier homogen
y 00 + ay 0 + by = 0
(3.12)
dengan koe…sien a dan b adalah suatu konstanta. Aplikasi dari persamaan ini
sangat penting, khususnya pada bidang mekanik dan getaran listrik. Solusi dari
persamaan (3.12), mengambil ide dari solusi persamaan diferensial linier orde
42
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
pertama y 0 + ky = 0 dengan k suatu konstanta, yaitu y = e kx . Dengan mengamati solusi dari persamaan diferensial linier orde pertama tersebut, diperoleh:
y=e
x
(3.13)
sebagai solusi dari persamaan (3.12).
Substitusikan (3.13) dan turunan-turunannya ke dalam persamaan (3.12), sehingga didapatkan persamaan ( 2 + a + b)e x = 0: Jika adalah solusi dari
persamaan kuadrat
2
+ a + b = 0;
(3.14)
maka persamaan (3.13) adalah solusi dari persamaan (3.12). Selanjutnya persamaan (3.14) ini disebut sebagai persamaan karakteristik dari persamaan
diferensial (3.12), dengan akar-akarnya sebagai berikut:
1
=
p
1
( a + a2
2
4b) ;
2
=
1
( a
2
p
a2
4b):
(3.15)
Fungsi-fungsi
y1 = e
1x
dan y2 = e
2x
(3.16)
menjadi solusi dari persamaan diferensial (3.12). Dengan mengaplikasikan
fungsi-fungsi (3.16) ke dalam persamaan (3.12), dapat diperiksa kebenaran dari
solusi tersebut. Dari persamaan (3.15), dapat diketahui bahwa akar-akar persamaan karakteristiknya bergantung kepada tanda dari diskriminan a2 4b;
sehingga solusi persamaan diferensial 3.12 dapat dibedakan dalam tiga kasus,
yaitu:
kasus I: dua akar real, jika a2
kasus II: akar dobel real, jika a2
4b > 0;
4b = 0;
kasus III: akar-akar kompleks, jika a2
4b < 0:
Berikut ini adalah pembahasan kasus per kasus.
Kasus I: Dua akar real yang berbeda,
1
dan
2:
Dalam kasus ini, y1 = e 1 x dan y2 = e 2 x merupakan basis dari solusi (3.12)
pada suatu interval (karena y1 =y2 bukan konstanta), sehingga solusi umumnya
adalah
y(x) = c1 e
1x
+ c2 e
2x
:
(3.17)
3.2. PERSAMAAN DENGAN KOEFISIEN KONSTANTA
43
Example 47 :
Berdasarkan rumus 3.17, persamaan diferensial y 00 y = 0 dapat diselesaikan
dengan cara yang lebih sistematik. Persamaan karakteristik untuk persamaan
diferensial tersebut adalah 2 1 = 0; dengan akar-akarnya adalah = 1 dan
= 1: Basis dari persamaan diferensial tersebut adalah y1 = ex dan y2 = e x ;
sehingga solusi umum dari persamaan diferensial tersebut adalah
y = c1 ex + c2 e
x
:
|
Example 48 :
Selesaikan masalah nilai awal berikut ini :
y 00 + y 0 2y = 0;
y(0) = 4; y 0 (0) = 5:
Jawab: :
Tahap pertama: mencari solusi umum:
Persamaan karakteristiknya
adalah 2 +
p
p2 = 0; dan akar-akarnya:
1
1 + 8) = 1 dan 1 = 21 ( 1
1 + 8) = 2:
1 = 2( 1 +
Jadi solusi umumnya adalah y = c1 ex + c2 e 2x :
Tahap kedua: mencari solusi masalah nilai awal:
Turunan pertama dari y tersebut adalah y 0 = c1 ex 2c2 e 2x :
Dengan memasukkan syarat awalnya, diperoleh:
y(0) = c1 + c2 = 4 dan y 0 (0) = c1 2c2 = 5; sehingga diperoleh c1 = 1 dan
c2 = 3:
Jadi solusi masalah nilai awalnya adalah y = ex + 3e 2x :
|
Kasus II: Akar Dobel Real,
=
a=2
Jika diskriminan a2 4b = 0; maka persamaan (3.15) hanya akan memberikan
satu akar, yaitu = 1 = 2 = a=2; sehingga solusi pertamanya adalah:
y1 = e
(a=2)x
:
(3.18)
Untuk mencari solusi keduanya, yang dibutuhkan sebagai basis, kita membentuk
y2 = uy1
(3.19)
dan menentukan fungsi u; sedemikian sehingga y2 menjadi solusi dari persamaan
diferensial (3.12). Substitusikan y2 = uy1 dan turunan-turunannya, yaitu
y20 = u0 y1 + uy10 dan y200 = u00 y1 + 2u0 y10 + uy100 ; ke dalam persamaan (3.12).
Persamaan baru yang diperoleh:
(u00 y1 + 2u0 y10 + uy100 ) + a(u0 y1 + uy10 ) + buy1 = 0:
Bila dikelompokkan berdasarkan fungsi u nya, menjadi:
u00 y1 + u0 (2y10 + ay1 ) + u(y100 + ay10 + by1 ) = 0:
Karena y1 solusi dari persamaan (3.12), maka y100 + ay10 + by1 = 0:
Karena 2y10 = ae (a=2)x = ay1 ; maka 2y10 + ay1 = 0, sehingga u00 y1 = 0:
Akibatnya, u00 = 0: Dengan dua kali pengintegralan, diperoleh u = c1 x + c2 :
Untuk mendapatkan solusi ke dua yang bebas, yaitu y2 = uy1 ; kita dapat
mengambil u = x; sehingga y2 = xy1 : Karena kedua solusi ini tidak proporsional, mereka membentuk basis. Basis dari solusi persamaan (3.12) adalah
y1 = e (a=2)x dan y2 = xe (a=2)x :
Jadi solusi umumnya adalah
y(x) = (c1 + c2 x)e
(a=2)x
:
(3.20)
44
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Example 49 :
Selesaikan persamaan berikut: y 00 + 8y 0 + 16y = 0:
Jawab:
Persamaan karakteristiknya adalah: 2 + 8 + 16 = 0.
Karena a2 4b = (8)2 4(16) = 0; maka akarnya dobel, yaitu:
= a=2 = 8=2 = 4; sehingga basisnya adalah e 4x dan xe
Jadi solusi umumnya adalah y = (c1 + c2 x)e 4x :
|
4x
:
Example 50 :
Selesaikan masalah nilai awal berikut ini:
y 00 4y 0 + 4y = 0; y(0) = 3; y 0 (0) = 1:
Jawab:
Persamaan karakteristiknya adalah 2 4 + 4 = 0:
Karena a2 4b = 16 4(4) = 0; maka akarnya merupakan akar dobel,
yaitu = a=2 = 4=2 = 2:
Solusi umumnya adalah y = (c1 + c2 x)e2x :
Turunan pertama dari solusi umumnya adalah
y 0 = c2 e2x + 2(c1 + c2 x)e2x :
Dengan memasukkan syarat awal ke dalam solusi umum, diperoleh :
y(0) = c1 = 3; dan y 0 (0) = c2 + 2c1 = 1:
Dengan substitusi diperoleh c1 = 3 dan c2 = 5:
Jadi solusi khususnya adalah y = (3 5x)e2x :
|
Kasus III: Kasus Akar Kompleks
Untuk persamaan diferensial linier homogen dengan koe…sien konstanta (3.12),
akar-akar persamaan karakteristiknya adalah:
1
=
1p 2
1
a+
a
2
2
4b dan
2
=
1
a
2
1p 2
a
2
4b;
yang merupakan akar kompleks. Karena a2 4b < 0; maka
r
p
1 2
2
a
4b = ( 1)(4)(b
a ) = 2i !;
4
q
p
dengan i = ( 1) dan ! = b 41 a2 ; sehingga
1
=
1
a + i! dan
2
2
=
1
a
2
i!:
(3.21)
Pada pembahasan sebelumnya, diketahui bahwa e 1 x dan e 2 x adalah solusi
kompleks dari persamaan (3.12), sehingga basis solusi real dari persamaan (3.12)
pada suatu interval adalah:
y1 = e
(a=2)x
cos !x dan
y2 = e
(a=2)x
sin !x:
(3.22)
Karena y2 =y1 = tan !x 6= konstanta dan ! 6= 0; maka y1 dan y2 tidak proporsional. Jadi solusi umumnya adalah
y(x) = e
(a=2)x
(A cos !x + B sin !x):
(3.23)
3.2. PERSAMAAN DENGAN KOEFISIEN KONSTANTA
45
Example 51 :
Tentukan solusi umum dari persamaan y 00
2y 0 + 10y = 0:
Jawab:
Persamaan karakteristiknya adalah
Karena a2
1
4b = 4
= 1 + 3 i dan
2
40 =
=1
2
2 + 10 = 0:
36 < 0; maka akarnya kompleks, yaitu
3 i:
Basisnya adalah y1 = ex cos 3x dan y2 = ex sin 3x:
Jadi solusi umumnya adalah y(x) = ex (A cos 3x + B sin 3x):
Example 52 :
Selesaikan masalah nilai awal berikut ini:
y 00 + 2y 0 + 5y = 0;
y(0) = 1;
y 0 (0) = 5:
|
46
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Jawab:
Persamaan karakteristiknya adalah: 2 + 2 + 5 = 0:
Karena a2 4b = 4 20 = 16 < 0; maka akarnya kompleks, yaitu
1 + 2 i dan 2 = 1 2 i:
1 =
Solusi umumnya adalah y = e x (A cos 2x + B sin 2x):
Turunan pertama dari solusi umumnya adalah
y0 = e
x
( A cos 2x
B sin 2x
2A sin 2x + 2B cos 2x):
Dengan memasukkan syarat awalnya, diperoleh:
y(0) = A = 1:
y 0 (0) = A + 2B = 1 + 2B = 5; maka B = 3:
Jadi solusi masalah nilai awalnya adalah y(x) = e
x
(cos 2x + 3 sin 2x):
|
Example 53 :
Selesaikan persamaan diferensial: y 00 + ! 2 y = 0:
Jawab:
Persamaan karakteristiknya adalah: 2 + ! 2 = 0:
Karenapa2 4b = 0 4! 2 = 4! 2 <
p 0; maka akarnya kompleks, yaitu
1
4! 2 = ! i dan 2 = 21
4! 2 = ! i:
1 = 2
Jadi solusi umumnya adalah y(x) = A cos !x + B sin !x:
|
Fungsi Eksponensial Kompleks
De…nition 4 :
Fungsi eksponensial kompleks ez dari peubah kompleks z = s + it; adalah
ez = es+it = es (cos t + i sin t):
Jika z =
1x
dengan
1
(3.24)
seperti pada (3.25), maka
1
ax + i!x:
2
Dengan mensubstitusikan z ke dalam persamaan (3.28), diperoleh:
z = s + it =
(a=2)x + i ! x
e
Karena sin (
)=
e
1x
= e
=
(a=2)x
(cos !x + i sin !x):
2x
sin ; maka untuk e
(a=2)x
i!x
= e
(a=2)x
diperoleh:
(cos !x
i sin !x):
Bila s = 0; maka
eit = cos t + i sin t
(3.25)
yang disebut sebagai ”Rumus Euler”.
Rangkuman :
Kasus
I
II
Akar-akar pers.
karakteristik
Akar real :
e
2
1x
;e
2x
Solusi umum pers.
homogen
y(x) = c1 e
1x
+ c2 e
2x
Akar dobel real :
=
III
1;
Basis pers.
homogen
a=2
e
(a=2)x
; xe
(a=2)x
y(x) = (c1 + c2 x)e
(a=2)x
Akar kompleks :
=
2 =
1
1
2a +
1
2a
i!
i!
e
e
(a=2)x
(a=2)x
cos !x
sin !x
y(x) = e (a=2)x (A cos !x
+ B sin !x)
3.2. PERSAMAAN DENGAN KOEFISIEN KONSTANTA
47
Masalah Nilai Batas
Persamaan homogen y 00 + ay 0 + by = 0 dengan syarat batas: y(P1 ) = k1 ; dan
y(P2 ) = k2 ; pada suatu interval I, membentuk suatu ’masalah nilai batas’.
Example 54 :
Selesaikan masalah nilai batas berikut:
y 00 + y = 0; y(0) = 3; y( ) = 3:
Jawab:
Persamaan karakteristiknya adalah 2 + 1 = 0:
Akar-akarnya adalah 1 = i dan 2 = i:
Basis dari persamaan homogennya adalah y1 = cos x dan y2 = sin x:
Solusi umumnya adalah: y(x) = A cos x + B sin x:
Dengan memasukkan syarat batasnya diperoleh:
y(0) = 3; sehingga A = 3 dan
y( ) = 3; sehingga A cos( ) + B sin( ) = A + 0 = A = 3 ) A = 3:
Karena tidak diperoleh nilai untuk konstanta B; maka solusi khususnya masih
memuat konstanta B:
Jadi solusi masalah nilai batasnya adalah y(x) = 3 cos x + B sin x; dengan B
konstanta sebarang.
|
3.2.2
Latihan
I. Selesaikan persamaan diferensial berikut:
1. y 00
25y = 0:
2. y 00 + 6y 0 + 9y = 0:
3. 10y 00 + 6y 0 + 10; 9y = 0:
II. Selesaikan masalah nilai awal berikut:
4. y 00 + 9y = 0; y( ) =
5. y 00
2; y 0 ( ) = 3:
4y 0 + 4y = 0; y(0) = 3; y 0 (0) = 10:
6. y 00 + 2y 0 + 2y = 0; y(0) = 1; y 0 (0) = 0:
7. y 00
6y 0 + 18y = 0; y(0) = 0; y 0 (0) = 6:
III. Selesaikan masalah nilai batas berikut:
8. y 00
9. y 00
10. y 00
16y = 0; y(0) = 5; y( 41 ) = 5e:
2y 0 = 0; y(0) =
1; y( 12 ) = e
2y 0 + 2y = 0; y(0) =
2:
3; y( 12 ) = 0:
48
3.2.3
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Persamaan diferensial linier homogen orde ke-n
Pandang persamaan diferensial linier homogen orde ke-n dengan koe…sien konstanta:
y (n) + an 1 y (n 1) + ::: + a1 y 0 + a0 y = 0:
(3.26)
Ide dari solusi persamaan diferensial tersebut di atas adalah sama dengan n = 2:
Dengan mensubstitusikan y = e x dan turunan-turunannya, diperoleh persamaan karakteristik:
n
+ an
1
n 1
+ ::: + a1 + a0 = 0:
(3.27)
Untuk mendapatkan solusi dari persamaan (3.26) tersebut, kita harus menentukan akar-akar dari persamaan (3.27). Pada prakteknya hal ini agak sulit dan
harus diselesaikan dengan menggunakan metode numerik, kecuali kita dapat
menebaknya atau mencarinya dengan cara trial and error.
Kasus I : Akar Real yang berbeda
Jika persamaan (3.27) mempunyai n akar real yang berbeda, yaitu
maka akan kita jumpai sebanyak n solusi:
y1 = e
1x
nx
; :::; yn = e
1;
:::;
n;
;
(3.28)
nx
(3.29)
dan solusi umumnya adalah:
y1 = c1 e
1x
+ ::: + cn e
:
Example 55 : Akar real yang berbeda
Selesaikan persamaan diferensial berikut : y 000
2y 00
y 0 + 2y = 0:
Jawab:
Persamaan karakteristiknya adalah 3 2 2
+ 2 = 0:
Akar-akarnya adalah 1 = 1; 2 = 1; dan 3 = 2.
Jadi solusi umumnya adalah: y = c1 e x + c2 ex + c3 e2x :
|
Theorem 7 : Basis
Solusi y1 = e 1 x ; :::; yn = e n x dari persamaan (3.26) (dengan
real atau
kompleks) membentuk basis solusi dari persamaan (3.26) jika dan hanya jika
semua n akar dari (3.27) berbeda.
Theorem 8 : Bebas Linier
Solusi-solusi y1 = e 1 x ; :::; yn = e m x ; dari (3.26) adalah bebas linier pada
interval terbuka I jika dan hanya jika 1 ; :::; m berbeda.
Kasus II : Akar Kompleks Sederhana
Jika terdapat akar-akar kompleks, mereka harus muncul secara berpasangan
(conjugate pairs), karena koe…sien dari (3.26) real. Jika = + i! adalah akar
i!; sehingga dua
sederhana dari (3.27), maka demikian pula dengan =
solusi yang berhubungan dengan akar-akar tersebut di atas adalah:
y1 = e
x
cos !x;
y2 = e
x
sin !x:
3.2. PERSAMAAN DENGAN KOEFISIEN KONSTANTA
49
Example 56 :
Selesaikan masalah nilai awal berikut:
y 000 2y 00 + 2y 0 = 0; y(0) = 0; 5; y 0 (0) =
1; dan y 00 (0) = 2:
Jawab:
Persamaan karakteristiknya adalah: 3 2 2 + 2 = 0:
Apabila disederhanakan, akan berbentuk: ( 2 2 + 2) = 0:
Akar-akarnya adalah 1 = 0; 2 = 1 + i; dan 3 = 1 i:
Basisnya adalah: y1 = e0x = 1; y2 = ex cos x; dan y3 = ex sin x:
Solusi umumnya adalah: y = c1 + ex (A cos x + B sin x):
Turunan-turunan dari y adalah:
y 0 = ex [(A + B) cos x + ( A + B) sin x] ; y 00 = ex [2B cos x 2A sin x] :
Dengan memasukkan syarat awalnya, diperoleh:
y(0)
y 0 (0)
y 00 (0)
= 0; 5; maka c1 + A = 0; 5:
=
1; maka A + B = 1:
= 2; maka 2B = 2 ) B = 1; sehingga A =
2 dan c1 = 2; 5:
Jadi solusi untuk masalah nilai awal tersebut di atas adalah:
y = 2; 5 + ex ( 2 cos x + sin x):
|
Kasus III: Akar Real Berlipat ganda (multiple)
Jika muncul akar real dobel, katakan 1 = 2 ; maka y1 = y2 adalah solusi dari
persamaan (3.28). Dua solusi bebas linier yang berhubungan dengan akar-akar
ini adalah: y1 dan y2 = xy1 : Jika akar lipat tiga muncul, katakan 1 = 2 = 3 ;
maka y1 = y2 = y3 adalah solusi dari persamaan (3.28). Tiga solusi bebas linier
yang berhubungan dengan akar-akar ini adalah: y1 ; xy1 , x2 y1 : Secara umum,
jika adalah akar dari orde-m; maka m solusi bebas linier yang berhubungan
dengan akar-akar tersebut adalah: y; xy, x2 y; ..., xm 1 y atau bila y = e x ;
maka m solusi bebas liniernya adalah: e x ; xe x , x2 e x ; ..., xm 1 e x :
Example 57 :
Selesaikan persamaan diferensial berikut: y v
3y iv + 3y 000
y 00 = 0:
Jawab:
2
Persamaan karakteristiknya adalah: 5 3 4 + 3 3
= 0:
Dengan menguraikan persamaan karakteristik tersebut akan diperoleh:
2 3
(
3 2+3
1) = 0 , 2 = 0 atau (
1)3 = 0;
sehingga akar-akarnya: 1 = 2 = 0 dan 3 = 4 = 5 = 1:
Jadi solusinya adalah: y = c1 + c2 x + (c3 + c4 x + c5 x2 )ex :
|
Kasus IV : Akar Kompleks Berlipat Ganda
Jika
= + i! adalah akar dobel kompleks dari persamaan (3.28), maka
i!: Solusi bebas linier yang berhubunpasangan conjugatenya adalah =
gan dengan akar-akar tersebut adalah: e x cos !x; e x sin !x; xe x cos !x dan
xe x sin !x; dengan e x cos !x dan e x sin !x berasal dari e x dan e x ; sedangkan xe x cos !x dan xe x sin !x berasal dari xe x dan xe x : Untuk akar tripel
kompleks, solusi bebas liniernya adalah e x cos !x; e x sin !x; xe x cos !x; xe x sin !x;
x2 e x cos !x; dan x2 e x sin !x:
50
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Example 58 :
Selesaikan y (7) + 18y (5) + 81y 000 = 0:
Jawab:
Persamaan karakteristiknya adalah:
Bila diuraikan akan menjadi:
7
+ 18
5
+ 81
3
7
+ 18
5
+ 81
3
= 0:
3
( 4 + 18 2 + 81)
( 2 + 9)2
3
[( + 3i)(
3i)]2 ;
=
=
=
3
sehingga persamaan karakteristik tersebut mempunyai akar-akar:
tiga akar kembar real, 1 = 2 = 3 = 0 dan akar kompleks 4 = 5 = 3i; dan
3i:
6 = 7 =
Dengan = 0 dan ! = 3 pada akar kompleksnya, maka solusi umumnya adalah:
y = c1 + c2 x + c3 x2 + A1 cos 3x + B1 sin 3x + x(A2 cos 3x + B2 sin 3x):
3.2.4
|
Latihan
I. Tentukan solusi umum dari persamaan diferensial berikut ini:
1. y 000
y 0 = 0:
2. y 000
y 00
y 0 + y = 0:
3. y iv + 2y 00 + y = 0:
4. y iv
5y 00 + 4y = 0
II. Selesaikan masalah nilai awal berikut:
5. y 000 = 0; y(2) = 12; y 0 (2) = 16; y 00 (2) = 8:
6. y 000
3.3
2y 00
y 0 + 2y = 0; y(0) = 3; y 0 (0) = 0; y 00 (0) = 3:
Persamaan Euler-Cauchy
Pada persamaan homogen dengan koe…sien konstanta, solusinya dapat dengan
mudah ditentukan dengan tanpa menggunakan integral. Persamaan EulerCauchy orde ke-dua berikut
x2 y 00 + axy 0 + by = 0
(3.30)
juga dapat diselesaikan hanya dengan penghitungan aljabar biasa. Substitusikan: y = xm dan turunan-turunannya pada persamaan diferensial (3.30),
sehingga diperoleh:
x2 m(m
1)xm 2 + axmxm 1 + bxm = 0
m(m 1)xm + amxm + bxm = 0
xm [m2 + (a 1)m + b] = 0:
Bagi persamaan di atas dengan xm ; yang tidak sama dengan nol jika x 6= 0;
diperoleh suatu persamaan tambahan (auxiliary equation):
m2 + (a
1)m + b = 0
(3.31)
Seperti pada persamaan karakteristik, persamaan tambahan ini dapat diuraikan
ke dalam tiga kasus, tergantung dari diskriminan (a 1)2 4b:
3.3. PERSAMAAN EULER-CAUCHY
51
Kasus I: Akar Real yang Berbeda, m1 dan m2
Akar real yang berbeda diperoleh apabila (a 1)2 4b > 0; yang menghasilkan
akar-akar m1 dan m2 ; yang mana akar-akar ini akan membentuk basis
y1 (x) = xm1 dan y2 (x) = xm2
dari solusi persamaan diferensial (3.31) untuk semua x; dengan fungsi tersebut
terde…nisi. Solusi umumnya adalah
y(x) = c1 xm1 + c2 xm2
(3.32)
dengan c1 ; c2 sebarang.
Example 59 :
Selesaikan persamaan Euler-Cauchy berikut : x2 y 00
2; 5xy 0
2y = 0:
Jawab:
Persamaan tambahan untuk persamaan Euler-Cauchy di atas adalah
m2 3; 5m 2 = 0:
Akar-akarnya adalah m1 = 0; 5 dan m2 = 4:
Basis dari solusi real untuk semua x positif adalah:
y1 = x 0;5 = p1x dan y2 = x4 :
Jadi solusi umumnya adalah
c1
y(x) = p + c2 x4 :
x
|
Kasus II: Akar Dobel Real
Akar dobel real diperoleh jika (a 1)2 4b = 0. Jika persamaan (3.31) mempunyai akar dobel m1 = m2 = m = 12 (1 a); maka diperoleh solusi pertama
1
y1 = x 2 (1
a)
dan y2 : Solusi ke dua y2 dibentuk dari perkalian suatu fungsi u dengan solusi pertama y1 : Substitusikan y2 = uy1 dan turunan-turunannya ke dalam persamaan
(3.30), sehingga diperoleh:
x2 (u00 y1 + 2u0 y10 + uy100 ) + ax(u0 y1 uy10 ) + buy1 = 0:
u x y1 + u0 x(2xy10 + ay1 ) + u(x2 y100 + axy10 + by1 ) = 0:
(3.33)
00 2
Karena y1 solusi dari persamaan (3.30), maka x2 y100 + axy10 + by1 = 0:
Sedangkan
2xy10 + ay1
=
=
1
1
1
2x[ (1 a)x 2 (1 a) 1 ] + ax 2 (1 a)
2
1
1
1
(1 a)x 2 (1 a) + ax 2 (1 a) = x 2 (1
a)
= y1 :
Dengan demikian, persamaan (3.33) menjadi:
u00 x2 y1 + u0 xy1 = (u00 x2 + u0 x)y1 = 0:
Bagi persamaan di atas dengan y1 (6= 0); pisahkan peubahnya dan integralkan,
maka untuk x > 0; kita dapatkan:
u00 x2 + u0 x =
ln ju0 j =
0)
u00
=
u0
1
x
ln jxj ) u0 =
1
) u = ln x:
x
52
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Jadi y2 = y1 ln x; yang tidak proporsional terhadap y1 :
Dalam kasus akar dobel dari persamaan (3.31), basis dari persamaan (3.30)
untuk semua x positif adalah:
y1 = xm dan y2 = xm ln x;
dengan m = 21 (1
a): Jadi solusi umumnya adalah:
1
y(x) = (c1 + c2 ln x) x 2 (1
a)
;
c1 ; c2 sebarang
(3.34)
Example 60 :
Selesaikan persamaan Euler-Cauchy berikut: x2 y 00
3xy 0 + 4y = 0:
Jawab:
Persamaan tambahan untuk persamaan di atas adalah m2 4m + 4 = 0:
Akar-akarnya merupakan akar dobel real, yaitu m1 = m2 = m = 2:
Basis solusi real untuk semua x positif : y1 = x2 dan y2 = x2 ln x:
Jadi solusi umumnya adalah y(x) = (c1 + c2 ln x)x2 :
|
Kasus III: Akar Kompleks
Akar kompleks diperoleh jika (a 1)2 4b < 0: Jika akar-akar m1 dan m2 kompleks, maka m1 dan m2 dapat dituliskan sebagai m1 = +i v dan m2 =
i v:
Untuk menentukan basis dari solusi persamaan Euler-Cauchy, pertama-tama
tulis xk = (eln x )k = ek ln x ; yang dapat dikembangkan dari real ke kompleks.
Dengan mengganti k = i v dan bersama-sama dengan persamaan (3.29) (dengan
s = 0) diperoleh:
xi v
x
iv
= ei v ln x = cos (v ln x) + i sin (v ln x);
= e i v ln x = cos (v ln x) i sin (v ln x):
Kalikan dua persamaan di atas dengan x ; sehingga menghasilkan
x :xi v
x :x i v
= x
= x
+ iv
iv
= xm1 = x [ cos (v ln x) + i sin (v ln x)]
= xm2 = x [cos (v ln x) i sin (v ln x)]:
Apabila dua persamaan di atas dijumlahkan dan dikurangkan, akan menghasilkan:
xm1 + xm2
xm1 xm2
= 2x [ cos (v ln x)]
= 2x [i sin (v ln x)]:
Tulis y1 = x [ cos (v ln x)] dan y2 = x [sin (v ln x)]; maka
1 m1
1 m1
(x + xm2 ) = y1 dan
(x
2
2i
xm2 ) = y2 :
Berdasarkan penjelasan di atas, maka pada kasus akar kompleks ini, basis dari
solusi (3.30) untuk semua x positif adalah
y1 = x cos(v ln x); dan y2 = x sin(v ln x):
Fungsi-fungsi tersebut tidak proporsional dan merupakan solusi dari (3.30).
Jadi solusi umumnya adalah:
y(x) = x [A cos (v ln x) + B sin (v ln x)]:
(3.35)
3.3. PERSAMAAN EULER-CAUCHY
53
Example 61 :
Selesaikan persamaan berikut : x2 y 00 + 7xy + 13y = 0:
Jawab:
Persamaan tambahan: m2 + 6m + 13 =
p0:
Akar-akarnya adalah m1;2 = 12 :(6)
9 13 = 3 2 :
Jadi solusi umumnya adalah: y(x) = x 3 [A cos (2 ln x) + B sin (2 ln x)]:
|
Rangkuman :
Kasus
Akar-akar pers.
tambahan
I
Akar real
II
Akar dobel real
m=
III
m1 ; m 2
1
2 (1
Basis solusi pers.
Euler-Cauchy
Solusi umum pers.
Euler-Cauchy
y1 = xm1 ; y2 = xm2
y(x) = c1 xm1 + c2 xm2
1
a)
y1 = x 2 (1
1
y2 = x 2 (1
a)
a)
;
ln x
y(x) = (c1 + c2 ln x) :
1
x 2 (1 a)
Akar kompleks
m1 = + i v
y1 = x cos(v ln x)
y(x) = [A cos (v ln x)
m2 =
iv
y2 = x sin(v ln x)
+ B sin (v ln x)]:x
Untuk persamaan Euler-Cauchy orde ke-3 yang berbentuk:
x3 y 000 + ax2 y 00 + bxy 0 + cy = 0;
(3.36)
persamaan tambahannya dapat dicari dengan cara yang sama seperti pada persamaan Euler-Cauchy orde ke-2.
Ambil y = xm ; maka turunan-turunannya adalah:
y 0 = mxm 1 ; y 00 = m(m 1)xm 2 ; dan
y 000 = m(m 1)(m 2)xm 3 :
Hasil substitusi y; y 0 ; y 00 dan y 000 ke dalam persamaan di atas,
x3 m(m 1)(m 2)xm 3 + ax2 m(m 1)xm 2 + bx mxm 1 + cxm = 0:
m(m 1)(m 2)xm + a [m(m 1)xm ] + b [mxm ] + cxm = 0:
Bagi persamaan tersebut dengan xm (6= 0); sehingga diperoleh persamaan tambahan sebagai berikut:
m(m
m3
1)(m 2) + am(m 1) + bm + c = 0:
3m2 + 2m + am2 am + bm + c = 0
m3 + (a 3)m2 + (b a + 2)m + c = 0:
(3.37)
Example 62 : MNA untuk persamaan Euler-Cauchy orde ke-tiga.
Selesaikan MNA berikut:
x3 y 000 3x2 y 00 + 6xy 0 6y = 0; y(1) = 2; y 0 (1) = 1; y 00 (1) = 4;
pada suatu interval I pada sumbu x positif yang memuat x = 1:
Jawab:
Tahap pertama, mencari solusi umum:
Ambil y = xm ; maka turunan-turunannya adalah:
y 0 = mxm 1 ; y 00 = m(m 1)xm 2 ; dan
y 000 = m(m 1)(m 2)xm 3 :
Hasil substitusi y; y 0 ; y 00 dan y 000 ke dalam persamaan diferensial di atas,
x3 m(m 1)(m 2)xm 3
3x2 m(m 1)xm 2 + 6x mxm 1
6xm = 0:
54
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
m(m 1)(m 2)xm 3 [m(m 1)xm ] + 6 [mxm ] 6xm = 0:
Karena xm 6= 0; untuk x =
6 0; maka persamaan tambahannya:
m(m
m3
1)(m 2) 3m(m 1) + 6m
3m2 + 2m 3m2 + 3m + 6m
m3 6m2 + 11m
6 = 0:
6 = 0
6 = 0:
Dengan menebak akar m = 1; maka diperoleh akar-akar yang lain, yaitu: m = 2
dan m = 3: Jadi solusi umumnya adalah: y = c1 x + c2 x2 + c3 x3 :
Untuk orde yang lebih tinggi daripada 4, harus digunakan metode pencarian
akar secara numerik, seperti cara Newton, yang tidak akan dijelaskan dalam
pembahasan ini.
Tahap ke dua, mencari solusi khusus:
Turunan-turunan dari solusi umum y tersebut di atas adalah:
y 0 = c1 + 2c2 x + 3c3 x2 ; dan y 00 = 2c2 + 6c3 x: Dengan memasukkan syarat
awalnya, diperoleh :
y(1) = 2 ) c1 + c2 + c3 = 2; y 0 (1) = 1 ) c1 + 2c2 + 3c3 = 1; y 00 (1) = 4 )
2c2 + 6c3 = 4: Dengan menggunakan eliminasi, diperoleh: c1 = 2; c2 = 1; dan
c3 = 1:
Jadi solusi untuk masalah nilai awal tersebut di atas adalah:
y = 2x + x2
3.3.1
x3 :
|
Latihan
I. Selidiki apakah fungsi-fungsi yang diberikan merupakan solusi dari masalah
nilai awal berikut:
1. x2 y 00
3xy 0 + 4y = 0; y(1) = 2; y 0 (1) = 5; x2 ; x2 ln x:
2. xy 000 + 3y 00 = 0; y(1) = 4; y 0 (1) =
8; y 00 (1) = 10; dan 1; x; x
1
:
II. Tentukan solusi umum dari persamaan diferensial berikut ini:
3. xy 00 + 4y 0 = 0
4. x2 y 00 + 6; 2xy 0 + 6; 76y = 0:
5. x3 y 000 + 2x2 y 00
4xy 0 + 4y = 0:
6. x3 y 000 + 5x2 y 00 + 2xy 0
2y = 0:
III. Selesaikan masalah nilai awal berikut ini:
7. 4x2 y 00 + 4xy 0
8. x2 y 00
3.4
y = 0;
xy 0 + 2y = 0;
y(4) = 2;
y(1) =
y 0 (4) =
0; 25
1; y 0 (1) =
1
Persamaan Nonhomogen
Perhatikan persamaan linier nonhomogen orde ke-dua:
y 00 + p(x)y 0 + q(x)y = r(x);
(3.38)
dengan r(x) 6= 0: Persamaan linier homogennya dapat ditulis sebagai berikut:
y 00 + p(x)y 0 + q(x)y = 0
(3.39)
3.4. PERSAMAAN NONHOMOGEN
55
De…nition 5 :
Solusi umum dari persamaan nonhomogen (3.38) pada interval terbuka I, adalah
solusi yang berbentuk:
y(x) = yh (x) + yk (x);
(3.40)
dengan:
yh (x) = c1 y1 (x) + c2 y2 (x) adalah solusi umum persamaan homogen (3.39) pada
I, dan
yk (x) adalah solusi khusus dari persamaan nonhomogen (3.38) yang tidak memuat
konstanta sebarang.
Pada materi sebelumnya, sudah dijelaskan bagaimana mencari solusi umum yh :
Selanjutnya akan dibahas bagaimana mencari solusi khusus yk : Secara umum,
ada dua metoda yang dapat digunakan untuk mencari solusi khusus yk ; yaitu
metoda koe…sien taktentu dan metoda variasi parameter.
3.4.1
Metoda Koe…sien Taktentu Orde ke-dua
Pandang persamaan linier nonhomogen orde ke-dua dengan koe…sien konstanta:
y 00 + ay 0 + by = r(x)
(3.41)
dan r(x); yang dapat berupa: fungsi eksponensial, fungsi polinomial, fungsi cosinus, fungsi sinus, dsb. Dari fungsi-fungsi r(x) yang mungkin tersebut, dapat
diketahui bahwa r(x) mempunyai turunan yang mirip dengan dirinya sendiri.
Hal ini memberikan suatu ide untuk memilih yk yang berbentuk mirip dengan
r(x) dan memuat suatu koe…sien yang tak diketahui, yang nantinya akan ditentukan dengan jalan mensubstitusikan yk tersebut ke dalam persamaan (3.41).
Example 63 :
Tentukan solusi khusus yk dari persamaan diferensial berikut ini:
y 00 + 3y 0 + 4y = 3x + 2:
Jawab:
Diketahui r(x) = 3x + 2; suatu fungsi polinomial berderajat satu.
Pilih yk = Ax + B; maka yk0 = A dan yk00 = 0:
Substitusi dari yk ; yk0 dan yk00 ke dalam persamaan diferensial di atas, menghasilkan:
(0) + 3(A) + 4(Ax + B) = 3x + 2:
4Ax + (3A + 4B) = 3x + 2
4A = 3 ) A = 3=4;
3A + 4B = 2 ) B = 1=16:
Jadi solusi khusus yk untuk persamaan diferensial di atas adalah
yk (x) =
3
x
4
1
:
16
Example 64 :
Tentukan solusi khusus dari y 00
Jawab:
4y = 2e3x :
|
56
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Turunan dari e3x adalah suatu konstanta kali e3x :
Pilihan yang masuk akal untuk solusi khususnya adalah yk = Ae3x :
Turunan pertama dan keduanya adalah
yk0 = 3Ae3x dan yk00 = 9Ae3x :
9Ae3x
4(Ae3x ) = 2e3x ; sehingga
5A = 2; A = 25 :
Jadi solusi khususnya adalah yk (x) = 25 e3x :
|
Example 65 :
Tentukan solusi khusus dari persamaan diferensial:
3y 00 + y 0
2y = 2 cos x:
Jawab:
Menurut perkiraan, solusi khususnya adalah A cos x:
Dengan adanya y 0 yang memuat sin x; maka pilihan untuk solusi
khususnya adalah: yk = A cos x + B sin x:
Turunan-turunan dari yk tersebut adalah:
yk0 =
A sin x + B cos x dan
yk00 =
A cos x
B sin x:
Substitusikan ke dalam persamaan diferensial di atas.
Hasilnya adalah: ( 5A + B) cos x + ( A
sehingga
5A + B = 2 dan
A
5B) sin x = 2 cos x;
5B = 0:
Dengan eliminasi diperoleh hasil: A =
5
13
dan B =
1
13 :
Jadi solusi khususnya adalah:
yk (x) =
5
1
cos x +
sin x:
13
13
Example 66 :
Tentukan solusi khusus dari y 00
4y = 2e2x :
|
3.4. PERSAMAAN NONHOMOGEN
57
Jawab:
Jika dicoba memilih yk = Ae2x ; maka akan diperoleh:
yk00 4yk = 4Ae2x 4Ae2x = 0 6= 2e2x ; sehingga tidak memenuhi persamaan
nonhomogen di atas. Dalam hal ini ternyata pemilihan solusi khusus yk di atas
hanya sesuai untuk persamaan diferensial yang homogen. Oleh sebab itu dicoba
yk lain yang memuat e2x dan suatu (fungsi) yang lain yang nantinya apabila
disubstitusikan ke dalam persamaan diferensial di atas tidak sama dengan nol
(dapat diselesaikan). Perkiraan yang masuk akal adalah yk = Axe2x ; dengan
turunan-turunannya sebagai berikut:
yk0 = Ae2x + 2Axe2x dan yk00 = 4Ae2x + 4Axe2x :
Bila disubstitusikan ke dalam persamaan diferensial di atas akan menghasilkan:
4Ae2x + 4Axe2x
4(Axe2x )
=
2e2x :
4Ae2x
=
2e2x ) A =
Jadi solusi khususnya adalah yk (x) = 12 xe2x :
1
:
2
|
Dari contoh-contoh tersebut di atas, dapat diketahui bahwa pemilihan yk
yang mirip dengan r(x) tidak selalu dapat menyelesaikan masalah. Ada suatu
metode umum (yang selama ini selalu berhasil) dan lebih sederhana, yang dinamakan
”metode koe…sien taktentu”, yang dapat digunakan untuk mencari solusi
khusus yk : Metoda ini mempunyai tiga aturan, yaitu aturan dasar, aturan
modi…kasi dan aturan penjumlahan.
A. Aturan Dasar
Jika r(x) dari persamaan (3.41) adalah salah satu fungsi di dalam kolom I pada
tabel 2.1, pilihlah fungsi yk di dalam kolom II dan tentukan koe…sien taktentunya dengan jalan mensubstitusikan yk tersebut dan turunan-turunannya ke
dalam persamaan (3.41).
B. Aturan Modi…kasi
Jika yk yang dipilih ternyata merupakan solusi dari persamaan homogen yang
berhubungan dengan persamaan (3.41), maka kalikan yk yang dipilih dengan x
(atau x2 , jika solusi ini berhubungan dengan akar dobel persamaan karakteristik dari persamaan homogennya).
C. Aturan Penjumlahan
Jika r(x) adalah jumlah dari fungsi-fungsi yang terdaftar di dalam tabel 3.1.
kolom I, maka pilihlah yk yang merupakan jumlah fungsi-fungsi yang bersesuaian dari kolom ke dua.
58
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Keterangan:
1. Aturan Dasar memberitahukan apa yang seharusnya dilakukan secara
umum.
2. Aturan Modi…kasi menangani masalah-masalah yang mungkin muncul
pada suatu kasus tertentu.
3. Aturan Penjumlahan digunakan jika jumlah dua solusi dari persamaan
(3.41) dengan r = r1 dan r = r2 masing-masing adalah solusi dari (3.41)
dengan r = r1 + r2 :
Dalam menyelesaikan persamaan diferensial nonhomogen, langkah-langkah yang
harus dilakukan adalah:
Tahap I: mencari solusi umum persamaan homogennya yh
Tahap II: mencari solusi persamaan khusus yk
Tahap III: mencari solusi umum persamaan nonhomogennya (beserta masalah
nilai awalnya).
Tabel 3.1. Metode Koe…sien Taktentu
r(x)
Pilihan untuk yk
ke x
kxn (n = 0; 1; 2; :::)
k cos !x
k sin !x
ke x cos !x
ke x sin !x
Ce x
Kn xn + Kn 1 xn 1 + ::: + K1 x + K0
e
c K cos !x + M sin !x
e
c e x ( K cos !x + M sin !x)
Example 67 : Aplikasi Aturan Dasar (A)
Selesaikan persamaan nonhomogen: y 00 + 4y = 8x2 :
Jawab:
I. Mencari solusi umum persamaan homogennya: yh
Persamaan homogen: y 00 + 4y = 0:
Persamaan karakteristik: 2 + 4 = 0.
Akar-akarnya adalah: 1 = 2 i dan 2 = 2 i:
Solusi homogennya: yh = A cos 2x + B sin 2x:
3.4. PERSAMAAN NONHOMOGEN
59
II. Mencari solusi khusus: yk
Dari Tabel 3.1, pilihan untuk yk adalah: yk = K2 x2 + K1 x + K0 :
Turunan-turunan dari yk adalah:
yk0 = 2K2 x + K1 dan yk00 = 2K2 :
Substitusikan yk ; yk0 dan yk00 ke dalam persamaan nonhomogen di atas.
Hasilnya adalah:
2K2 + 4(K2 x2 + K1 x + K0 ) = 8x2 , 4K2 x2 + 4K1 x + 2K2 + 4K0 = 8x2 :
Akibatnya:
4K2 = 8 ) K2 = 2; 4K1 = 0 ) K1 = 0; 2K2 + 4K0 = 0 ) K0 = 1:
Solusi khususnya adalah yk = 2x2 1:
III. Jadi solusi umum persamaan nonhomogen di atas adalah:
y(x) = yh + yk = A cos 2x + B sin 2x + 2x2
1:
|
Example 68 : Aturan Modi…kasi (B)
Selesaikan persamaan nonhomogen: y 00
3y 0 + 2y = ex :
Jawab:
I. Persamaan karakteristik:
2
3 + 2 = 0:
Akar-akarnya adalah: 1 = 1 dan 2 = 2:
Solusi homogennya adalah: yh = c1 ex + c2 e2x :
II. Misalkan kita pilih yk = Cex :
Karena solusi dari persamaan homogennya memuat ex , maka harus
dipilih yk yang lain.
Pilih yk = Cxex ; dengan turunan-turunannya adalah:
yk0 = Cex + Cxex = C(ex + xex ) dan
yk00 = C(ex + ex + xex ) = C(2ex + xex ):
Hasil substitusi dari yk ; yk0 dan yk00 tersebut ke dalam persamaan
nonhomogen di atas adalah:
(2Cex 3Cex ) + (Cxex 3Cxex + 2Cxex ) = ex ; Cex = ex ) C =
Solusi khususnya adalah: yk = xex :
III. Jadi solusi umum untuk persamaan nonhomogen di atas adalah
y(x) = yh + yk = c1 ex + c2 e2x
xex :
Example 69 :
Selesaikan persamaan nonhomogen: y 00 + 9y = 2 sin 3x:
Jawab:
I. Persamaan karakteristik:
2
+ 9 = 0:
Akar-akarnya adalah: 1 = 3i dan 2 = 3i:
Jadi solusi homogennya adalah: yh = A cos 3x + B sin 3x:
|
1:
60
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
II. Misalkan kita pilih yk = K cos 3x + M sin 3x:
Karena solusi dari persamaan homogennya memuat sin 3x, maka harus dipilih
yk yang lain.
Pilih yk = Kx cos 3x + M x sin 3x; dengan turunan-turunannya adalah:
yk0
= K cos 3x 3Kx sin 3x + M sin 3x + 3M x cos 3x
= (K + 3M x) cos 3x + (M 3Kx) sin 3x
dan
yk00
= 3M cos 3x 3 (K + 3M x) sin 3x 3K sin 3x + 3(M
= 6M cos 3x 6K sin 3x 9M x sin 3x 9Kx cos 3x
= (6M 9Kx) cos 3x (6K + 9M x) sin 3x:
3Kx) cos 3x
Hasil substitusi dari yk ; yk0 dan yk00 tersebut ke dalam persamaan nonhomogen
di atas adalah:
(6M
9Kx) cos 3x
(6K + 9M x) sin 3x + 9 (Kx cos 3x + M x sin 3x) = 2 sin 3x
6M cos 3x 6K sin 3x = 2 sin 3x
Dari substitusi tersebut diperoleh
6M cos 3x =
M
=
0 dan
0 dan
Jadi solusi khususnya adalah: yk =
6K sin 3x = 2 sin 3x; sehingga
1
6K = 2 =) K =
:
3
1
3 x cos 3x
III. Jadi solusi umum untuk persamaan nonhomogen di atas adalah
y(x) = yh + yk = A cos 3x + B sin 3x
1
x cos 3x:
3
|
Example 70 :
Aturan Modi…kasi B (akar dobel) dan Aturan Penjumlahan (C).
Selesaikan masalah nilai awal berikut:
y 0 (0) = 0:
y 00
2y 0 + y = ex + x;
y(0) = 1;
3.4. PERSAMAAN NONHOMOGEN
61
Jawab:
I. Persamaan karakteristik:
2
2 + 1 = 0:
Akar-akarnya merupakan akar dobel, yaitu = 1:
Jadi solusi homogennya adalah yh = (c1 + c2 x)ex :
II. Karena r(x) merupakan jumlah dari dua fungsi, maka
r(x) = r1 + r2 = ex + x; dengan r1 = ex dan r2 = x:
Untuk r1 = ex , maka yk1 = Cx2 ex (karena akar dobel).
Dan untuk r2 = x; maka yk2 = K1 x + K0 :
Jadi pilihan untuk solusi khususnya adalah: yk = yk1 +yk2 = Cx2 ex +K1 x+K0 ;
dengan turunan-turunannya adalah
yk0 = 2Cxex + Cx2 ex + K1 ; dan yk00 = 2Cex + 4Cxex + Cx2 ex :
Substitusikan yk ; yk0 dan yk00 tersebut ke dalam persamaan nonhomogen
di atas, sehingga diperoleh hasil:
2Cex + K1 x 2K1 + K0 = ex + x:
Dengan membandingkan kedua sisi dalam persamaan tersebut diperoleh:
2Cex = ex ) C = 21 ; K1 x = x ) K1 = 1 ; dan 2K1 + K0 = 0 ) K0 = 2:
Jadi solusi khusus untuk persamaan nonhomogen tersebut di atas adalah: yk =
1 2 x
2 x e + x + 2:
III. Solusi umumnya adalah: y(x) = yh + yk = (c1 + c2 x)ex + 12 x2 ex + x + 2:
Turunan pertamanya adalah:
y 0 (x) = (c1 + c2 + c2 x)ex + (x + 12 x2 )ex + 1:
Dari syarat awal yang diberikan:
y(0) = 1 ) c1 + 2 = 1 ) c1 = 1;dan y 0 (0) = 0 ) c1 + c2 + 1 = 0 ) c2 = 0:
Jadi solusi untuk masalah nilai awal di atas adalah:
1
ex + x2 ex + x + 2:
2
y(x) =
3.4.2
|
Metoda Koe…sien Taktentu orde ke-n
Secara umum, persamaan diferensial linier nonhomogen orde ke-n dapat dituliskan sebagai berikut:
y (n) + pn
1 (x)y
(n 1)
+ ::: + p1 (x)y 0 + p0 (x)y = r(x);
(3.42)
dengan y (n) = dn y=dxn dan r(x) 6= 0: Jika r(x) = 0; maka
y (n) + pn
disebut homogen.
1 (x)y
(n 1)
+ ::: + p1 (x)y 0 + p0 (x)y = 0;
(3.43)
62
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
De…nition 6 :
Seperti pada persamaan nonhomogen orde ke-dua, solusi umum dari persamaan
nonhomogen (3.42) pada beberapa interval terbuka pada I adalah solusi yang
berbentuk:
y(x) = yh (x) + yk (x);
(3.44)
dengan yh (x) = c1 y1 (x) + ::: + cn yn (x) adalah solusi umum dari persamaan
homogen (3.43) pada I; dan yk (x) adalah solusi khusus dari (3.42) pada I;
yang tidak memuat konstanta sebarang. Sedangkan solusi khusus dari (3.42)
pada I adalah solusi yang diperoleh dari (3.44) dengan memasukkan nilai-nilai
tertentu pada konstanta sebarang c1 ; ..., cn di yh (x):
Metode koe…sien taktentu memberikan solusi khusus yk dari persamaan dengan
koe…sien konstanta
y (n) + an
1y
(n 1)
+ ::: + a1 y 0 + a0 y = r(x):
(3.45)
Penyelesaian persamaan (3.45) tersebut sama seperti untuk n = 2: Perbedaannya hanya pada Aturan Modi…kasi. Bila pada n = 2 persamaan karakteristik
dari persamaan homogennya hanya mempunyai akar sederhana atau akar dobel,
sedangkan persamaan karakteristik dari persamaan homogen:
y (n) + an
1y
(n 1)
+ ::: + a1 y 0 + a0 y = 0;
mempunyai akar berlipat ganda dari orde yang lebih besar, yaitu m (
Metode Koe…sien Taktentu
(3.46)
n):
A. Aturan Dasar (sama dengan aturan untuk n = 2 pada sub bab sebelumnya).
B. Aturan Modi…kasi.
Jika pilihan untuk yk adalah solusi dari persamaan homogen (3.46), maka kalikan yk (x) dengan xk ; dengan k adalah bilangan bulat positif terkecil, sehingga
tak ada lagi xk yk (x) yang merupakan solusi dari (3.46).
C. Aturan Penjumlahan (sama seperti pada sub bab sebelumnya).
Jadi untuk masalah nilai awal, ada tiga tahap yang harus dikerjakan:
1. Tahap I: menentukan solusi umum dari persamaan homogen (3.46).
2. Tahap II: memeriksa apakah aturan Modi…kasi perlu diterapkan, dan kemudian menentukan solusi khusus yk (x) dari (3.45).
3. Tahap III: menentukan solusi khusus dari (3.46) yang memenuhi syarat
awal yang diberikan.
Tabel 3.2 : Metode Koe…sien Taktentu
r(x)
Pilihan untuk yk
ke x
kxn (n = 0; 1; :::)
k cos !x
k sin !x
ke x cos !x
ke x sin !x
Ce x
Cn xn + Cn 1 xn 1 + ::: + C1 x + C0
K cos !x + M sin !x
e
x
(K cos !x + M sin !x)
3.4. PERSAMAAN NONHOMOGEN
63
Example 71 :
Selesaikan y iv
y = 30e
2x
:
Jawab:
Tahap I:
Persamaan karakteristiknya: 4 1 = 0:
Apabila diuraikan, menjadi ( 2 1)( 2 + 1) = 0; sehingga akar-akarnya adalah
: 1 = 1; 2 = 1; 3 = i dan 4 = i:
Jadi solusi homogennya adalah:
yh = c1 e x + c2 ex + c3 e ix + c4 eix atau yh = c1 e x + c2 ex + A cos x + B sin x:
Tahap II:
Karena semua akar berbeda (tidak ada akar dobel) dan pilihan untuk yk bukan
solusi dari persamaan homogennya, maka tidak perlu aturan Modi…kasi.
Pilih yk = Ce 2x dan turunan-turunannya adalah yk0 = 2Ce 2x ; ypiv =
16Ce 2x :
Substitusikan yk dan turunan-turunannya ke dalam persamaan diferensial yang
ada, sehingga diperoleh:
16Ce 2x Ce 2x = 30e 2x :
Bila diuraikan akan menghasilkan: C = 2; sehingga solusi khususnya adalah
yk = 2e 2x :
Jadi solusi umumnya adalah
y(x) = yh + yk = c1 e
x
+ c2 ex + A cos x + B sin x + 2e
2x
:
|
Example 72 : Aturan Modi…kasi
Tentukan solusi umum dari : y 000
3y 00 + 3y 0
y = 6ex :
Jawab:
Tahap I: mencari solusi umum persamaan homogennya: yh
Persamaan karakteristiknya adalah: 3 2 2 + 3
1 = 0; yang mempunyai
akar tripel yang sama, yaitu = 1: Oleh sebab itu solusi homogennya adalah:
yh = c1 ex + c2 xex + c3 x2 ex :
Tahap II: mencari solusi khusus persamaan nonhomogennya: yk :
Kita coba memilih yk = Cex ; maka apabila disubstitusikan ke dalam persamaan
diferensial di atas akan menghasilkan : C 3C + 3C C = 0 6= 6; sehingga
tidak ada solusi. Coba lagi untuk Cxex dan Cx2 ex : Karena Cex ; Cxex dan
Cx2 ex solusi homogen dari persamaan diferensial di atas, maka pilih yk sebagai
berikut: yk = Cx3 ex : Turunan-turunan dari yk tersebut adalah:
yk0 = C(x3 + 3x2 )ex ; yk00 = C(x3 + 6x2 + 6x)ex ; dan
yk000 = C(x3 + 9x2 + 18x + 6)ex :
Kemudian substitusikan yk dan turunan-turunannya tersebut ke dalam persamaan diferensial di atas, sehingga menghasilkan :
C(x3 + 9x2 + 18x + 6) 3C(x3 + 6x2 + 6x) + 3C(x3 + 3x2 ) Cx3 = 6:
Bila diuraikan akan menghasilkan: 6C = 6 ) C = 1:
Tahap III: Jadi solusi umumnya adalah: y(x) = yh +yk = (c1 +c2 x+c3 x2 ) ex +
x3 ex :
|
Example 73 : Masalah nilai awal
64
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Selesaikan masalah nilai awal berikut ini:
y 000 4y 00 + 4y 0 = 2x2 6x + 4; y(0) = 0; y 0 (0) =
5; y 00 (0) = 0:
Jawab:
I. mencari solusi umum persamaan homogennya: yh
2
2
Persamaan karakteristiknya adalah: 3 4 2 +4 =
4 +4 = (
2) =
0; yang mempunyai tiga akar, yaitu 1 = 0; dan 2 = 3 = 2 (kembar). Oleh
sebab itu solusi homogennya adalah: yh = c1 + c2 e2x + c3 xe2x :
II. mencari solusi khusus persamaan nonhomogen: yk
Pilihan untuk yk adalah yk = Kx2 + M x + N; sehingga turunan-turunannya
adalah:
yk0 = 2Kx + M ; yk00 = 2K; yk000 = 0: Dengan mensubstitusikan ke dalam persamaan diferensial di atas, diperoleh hasil: 0 2(2K) (2Kx + M ) + 2(Kx2 +
Mx
+
N)
=
2x2
6x
+
4:
Dengan menguraikan diperoleh hasil: K = 1; M = 2 dan N = 3:
Jadi solusi khususnya: yk = x2 2x + 3:
III. Dari tahap I dan II, diperoleh solusi umum persamaan nonhomogen:
y(x) = yh + yk = c1 + c2 e2x + c3 xe2x + x2 2x + 3:
Turunan dari solusi tersebut di atas adalah:
y 0 = 2c2 e2x + c3 e2x + 2c3 xe2x + 2x 2 dan
y 00 = 4c2 e2x + 2c3 e2x + 2c3 e2x + 4c3 xe2x + 2 = 4c2 e2x + 4c3 e2x + 4c3 xe2x + 2:
Dengan memasukkan syarat awalnya, akan diperoleh:
y(0) = c1 +c2 +3 = 0; y 0 (0) = 2c2 +c3 2 = 5; dan y 00 (0) = 4c2 +4c3 +2 = 0:
Dengan menggunakan eliminasi, diperoleh hasil:
c1 = 21 ; c2 = 52 ; dan c3 = 2:
Jadi solusi masalah nilai awal di atas adalah:
y(x) =
3.4.3
1
2
5 2x
e + 2xe2x + x2
2
2x + 3:
|
Latihan
I. Carilah solusi khusus yk dari persamaan nonhomogen berikut ini:
1. y 00 + 16y = e3x
2. y 00
y0
6y = 5 sin 2x
3. y 00
y0
2y = 3x + 4
4. y 00 + 2y 0
3y = 1 + xex
II. Tentukan solusi umumnya:
5. y 000 + 2y 00
6. y 000
y0
2y = 12e2x
y 0 = 10 cos 2x
7. y 000 + 3y 00 + 3y 0 + y = 16ex + x + 3:
III. Selesaikan masalah nilai awal berikut ini:
8. y 00 + 4y = 2x ; y(0) = 1; y 0 (0) = 2:
3.4. PERSAMAAN NONHOMOGEN
65
9. y 00 + 3y 0 + 2y = ex ; y(0) = 0; y 0 (0) = 3:
10. y 00 + 2y 0 + 2y = sin 3x ; y(0) = 2; y 0 (0) = 0:
11. y iv
5y 00 + 4y = 10 cos x;
12. y 000 + y 00
3.4.4
y(0) = 2; y 0 (0) = 0; y 00 (0) = 0; y 000 (0) = 0:
2y = 2x2 + 2x; y(0) =
1; y 0 (0) = 0; y 00 (0) =
4:
Metode Variasi Parameter
Metoda koe…sien taktentu hanya dapat menyelesaikan beberapa masalah persamaan linier nonhomogen dengan koe…sien konstanta saja, yang r(x) nya berupa
fungsi eksponensial, polinomial, sinus-cosinus, maupun jumlah atau perkalian
fungsi-fungsi tersebut. Bagaimana bila persamaan linier nonhomogennya berupa
persamaan Euler-Cauchy, yang merupakan persamaan dengan koe…sien peubah
? Bagaimana bila r(x) nya berupa fungsi tangen/cotangen, secan/cosecan, logaritma natural dan yang lainnya? Untuk dapat menyelesaikan persamaan linier
nonhomogen dengan r(x) yang beragam seperti itu diperlukan suatu metoda
yang tepat. Metoda ini dikenal sebagai metoda variasi parameter, yang pertama
kali diperkenalkan oleh Joseph Louis Lagrange (1736-1813). Metoda ini dapat
digunakan untuk menyelesaikan persamaan linier nonhomogen dengan koe…sien
konstanta maupun koe…sien peubah, jadi sifatnya lebih umum dan kompleks.
Perhatikan persamaan (3.42) dan (3.43). Solusi khusus yk untuk persamaan
(3.42) pada selang I; dengan koe…sien pada persamaan (3.42) dan r(x) nya
kontinu, dirumuskan sebagai berikut:
Z
Z
W2 (x)
W1 (x)
r(x)dx + y2 (x)
r(x)dx + ::: +
yk (x) = y1 (x)
W (x)
W (x)
Z
Wn (x)
+yn (x)
r(x)dx:
(3.47)
W (x)
Fungsi y1 ; y2 ; :::; yn membentuk basis solusi persamaan (3.43). W adalah
determinan Wronski atau Wronskian saja; dengan
y1
y10
:::
W (y1 ; y2 ; :::; yn ) =
y2
y20
:::
(n 1)
y1
(n 1)
y2
:::
yn
:::
yn0
:::
:::
(n 1)
::: yn
dan Wj (j = 1; 2; :::; n) diperoleh dari W dengan mengganti kolom ke j dari W
dengan kolom [000::::1]T :
Perhatikan persamaan linier nonhomogen orde ke-dua:
y 00 + p(x)y 0 + q(x)y = r(x);
dengan p; q dan r kontinu pada selang I: Misalkan y1 dan y2 membentuk basis
solusi dari persamaan homogen:
y 00 + p(x)y 0 + q(x)y = 0:
Determinan Wronskinya adalah
W (y1 ; y2 ) =
sedangkan W1 =
0 y2
1 y20
=
y2
y1
y10
y2
y20
dan
= y1 y20
W2 =
y2 y10 ;
y1
y10
0
1
= y1 :
66
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Berdasarkan rumus pada persamaan (3.47), solusi khusus yk untuk persamaan
linier nonhomogen orde ke-dua dapat dirumuskan sebagai berikut:
Z
Z
y2 :r
y1 :r
yk (x) = y1
dx + y2
dx:
(3.48)
W
W
Metoda variasi parameter ini lebih kompleks dalam pengerjaannya, dibandingkan dengan metoda koe…sien taktentu. Dalam metoda koe…sien taktentu,
penyelesaiannya lebih sederhana dan mudah, karena hanya menggunakan teknik
aljabar dan turunan biasa. Sedangkan dalam metoda variasi parameter, penyelesaiannya menggunakan teknik pengintegralan dan selalu menyertakan basis
solusi homogennya dalam menentukan solusi yk nya.
Example 74 :
Selesaikan persamaan diferensial berikut ini:
y 00 + y = sec x:
Jawab:
Persamaan homogen dari persamaan di atas adalah:
y 00 + y = 0:
2
Persamaan karakteristiknya:
+ 1 = 0:
Akar-akar persamaan karakteristiknya: 1 = i; dan 2 = i:
Basis solusi persamaan homogennya:
y1 = cos x; dan y2 = sin x:
Solusi homogennya: yh (x) = c1 cos x + c2 sin x:
Determinan Wronskinya adalah:
cos x sin x
= cos2 x ( sin2 x) = 1:
W (y1 ; y2 ) =
sin x cos x
Solusi khususnya diperoleh dari
Z
Z
yk (x) =
cos x sin x: sec xdx + sin x cos x: sec xdx
=
cos x ln jcos xj + x sin x:
Jadi solusi umumnya adalah:
y(x)
= yh (x) + yk (x)
= (c1 + ln jcos xj) cos x + (c2 + x) sin x:
|
Example 75 :
Tentukan solusi umum persamaan Euler-Cauchy berikut:
x3 y 000 3x2 y 00 + 6xy 0 6y = x4 ln x:
Jawab:
Persamaan homogen untuk persamaan Euler-Cauchy di atas adalah:
x3 y 000 3x2 y 00 + 6xy 0 6y = 0:
Persamaan tambahannya (auxiliary equation) adalah
m3 6m2 + 11m 6 = 0:
Akar-akar persamaan tambahannya adalah m1 = 1; m2 = 2; m3 = 3:
Basis solusi homogennya adalah y1 = x; y2 = x2 ; y3 = x3 :
Solusi umum persamaan homogennya adalah:
yh (x) = c1 x + c2 x2 + c3 x3 :
Karena rumus penentuan yk berlaku untuk bentuk standar persamaan linier
nonhomogen, maka sebelum dapat diterapkan ke dalam rumus yk di atas, persamaan Euler-Cauchy tersebut harus diubah dulu ke dalam bentuk standarnya,
yaitu:
3 00
6
6
y 000
y + 2 y0
y = x ln x:
x
x
x3
3.4. PERSAMAAN NONHOMOGEN
W (y1 ; y2 ; y3 ) =
x 0
1 0
0 1
W2 =
x x2 x3
1 2x 3x2
0 2
6x
x3
3x2
6x
=
3
2x ;
3
67
= 2x ; W1 =
W3 =
0 x2 x3
0 2x 3x2
1 2
6x
x x2 0
1 2x 0
0 2 1
= x4
= x2 :
Solusi khususnya adalah
yk (x)
Z
= y1
Z
= x
Z
= x
=
=
Z
Z
W1
W2
W3
:rdx + y2
:rdx + y3
:rdx
W
W
W
Z
Z
2x3
x2
x4
2
3
:x
ln
xdx
+
x
x
ln
xdx
+
x
x ln xdx
3
3
2x
2x
2x3
Z
Z
1
x
:x ln xdx x2 x ln xdx + x3
x ln xdx
2
2x
x x3
x3
x2
x2
x3
ln x
ln x
(x ln x x)
x2
+
2 3
9
2
4
2
11
x4
ln x
:
6
6
Jadi solusi umumnya adalah:
y(x) = yh (x) + yk (x) = c1 x + c2 x2 + c3 x3 +
3.4.5
x4
6
Latihan
Selesaikan persamaan linier nonhomogen berikut ini:
1. y 00 + 9y = sec 3x
2. y 00 + 4y = tan 2x
3. x3 y 000 + x2 y 00
2xy 0 + 2y = x3 ln x:
ln x
11
6
:
|
68
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
3.5
Aplikasi Persamaan Diferensial Linier Orde
Dua
Example 76 : Sirkuit RLC
Tentukan persamaan arus I sebagai fungsi dari t setelah saklar (switch) pada suatu sirkuit RCL ditutup. Sirkuit RLC terdiri dari resistor, induktor, kondensor
(kapasitor), baterai 12 volt, dan saklar yang semuanya tersusun seri. Diketahui
resistor R = 16 ohm, induktor L = 0; 02 henry, dan kondensor C = 2 10 4
farad. Asumsikan bahwa tidak ada muatan di kondensor sebelum saklarnya
ditutup, sehingga Q = 0; jika t = 0; juga I = 0 jika t = 0:
Jawab:
Diketahui R = 16 ohm, L = 0; 02 henry, C = 2 10 4 farad dan E(t) = 12 volt,
0
dan syarat awal Q (0) = 0 dan I(0) = dQ
dt (0) = Q (0) = 0: Berdasarkan hukum
voltase Kircho¤:
d2 Q R dQ
1
1
+
+
Q = E (t) :
(3.49)
2
dt
L dt
LC
L
Dengan memasukkan nilai-nilai R; L; C dan E(t); diperoleh persamaan nonhomogen sebagai berikut:
d2 Q
16 dQ
1
1
+
+
Q =
(12)
dt2
0; 02 dt
(0; 02) (2 10 4 )
0; 02
Q00 + 800Q0 + 250:000Q = 600:
Persamaan homogennya adalah
Q00 + 800Q0 + 250:000Q = 0:
Persamaan karakteristiknya adalah
2
+ 800 + 250:000
1;2
=
=
0
400
300i
Jadi solusi persamaan homogennya adalah
Qh (t) = e
400t
(A cos 300t + B sin 300t) :
Pilih solusi khususnya
Qk = K1
sehingga diperoleh turunan-turunannya sebagai berikut: Q0k = 0; Q00k = 0:
Substitusikan Qk dan turunan-turunannya ke dalam persamaan nonhomogennya, sehingga diperoleh
0 + 0 + 250:000K1
250:000K1
=
=
600
600 =) K1 = 2; 4
10
3
:
Jadi solusi khususnya adalah
Qk (t) = 2; 4
10
3
:
Solusi umum persamaan nonhomogennya adalah
Q(t)
= Qh (t) + Qk (t)
= e 400t (A cos 300t + B sin 300t) + 2; 4
10
3
:
3.5. APLIKASI PERSAMAAN DIFERENSIAL LINIER ORDE DUA
69
Dengan memasukkan syarat awal Q(0) = 0; diperoleh
A=
2; 4
10
3
:
Untuk mencari B; turunkan Q(t) sehingga diperoleh
Q0 (t)
=
400e
400t
(A cos 300t + B sin 300t) +
e
( 300A sin 300t + 300B cos 300t)
400t
= e
[( 400A + 300B) cos 300t + ( 400B
400t
Karena Q0 (0) = 0 dan A =
2; 4
10
3
300A) sin 300t] :
; maka
400A + 300B = 0 =) B =
3; 2
10
3
:
Solusi masalah nilai awalnya adalah
Q(t) = e
400t
2; 4
10
3
cos 300t +
3; 2
10
3
sin 300t + 2; 4
10
3
:
Jadi persamaan yang diharapkan untuk arus I sebagai fungsi dari t adalah
I(t) = Q0 (t) = 2e
400t
sin 300t:
|
Example 77 : Sirkuit RLC
Tentukan kuat arus I(t) dalam sirkuit RLC dengan R = 100 ohm, L = 0; 1
henry, dan C = 10 3 farad, yang terhubung dengan sumber voltase E(t) = 155
sin 377t (catatan: 60 Hz = 60 siklus/detik). Asumsikan tegangan Q dan kuat
arus I adalah nol jika t = 0:
Jawab:
Berdasarkan hukum voltase Kircho¤, model untuk sirkuit listrik RLC tersebut
adalah
EL + ER + EC = E(t):
(3.50)
R
Dengan EL = LI 0 ; ER = RI, Ec = 1c I(t)dt; dan E(t) = E0 sin !t; maka
hukum voltase Kircho¤ dapat dituliskan kembali sebagai
Z
1
0
LI + RI +
I(t)dt = E(t) = E0 sin !t:
(3.51)
C
Untuk menghilangkan integral dalam persamaan di atas, maka persamaan tersebut diturunkan sehingga diperoleh persamaan
LI 00 + RI 0 +
1
I = E0 ! cos !t:
C
(3.52)
Berdasarkan informasi pada soal, maka persamaan di atas menjadi persamaan
nonhomogen
0; 1I 00 + 100I 0 + 1000I = 155: (377) cos 377t:
Persamaan homogennya adalah
0; 1I 00 + 100I 0 + 1000I = 0 () I 00 + 1000I 0 + 10:000I = 0:
Persamaan karakteristiknya adalah
2
+ 1000 + 10:000 = 0;
70
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
yang menghasilkan akar-akar
990 dan
1
2
10;
sehingga solusi umumnya adalah
990t
I(t) = c1 e
+ c2 e
10t
:
Untuk mencari solusi persamaan nonhomogennya, pilih solusi khusus (steadystate current):
Ik (t) = A cos 377t + B sin 377t:
Dengan menurunkan rumus dasar
Ik (t) = A cos !t + B sin !t
sampai turunan pertama dan ke-dua, diperoleh rumus reaktansi S, nilai A dan
B sebagai berikut:
1
(377) (10
1
= (377) (0; 1)
!C
reaktansi S = !L
3)
= 35,
sehingga diperoleh
A=
E0 S
(155) : (35)
=
=
R2 + S 2
1002 + 352
0484 dan B =
E0 R
(155) : (100)
=
= 1; 38:
R2 + S 2
1002 + 352
Jadi solusi khususnya adalah
Ik (t) =
0; 484 cos 377t + 1; 38 sin 377t;
sehingga solusi umum (transient current) persamaan nonhomogennya adalah
I(t) = c1 e
990t
+ c2 e
10t
0; 484 cos 377t + 1; 38 sin 377t:
Dari syarat awal I(0) = 0; diperoleh persamaan
I(0) = c1 + c2
0; 484 = 0:
Untuk
memasukkan syarat
awal Q(0) = 0, digunakan persamaan LI 0 + RI +
R
R
1
I(t)dt = E(t) dan I(t)dt = Q(t); sehingga diperoleh persamaan
C
I 0 (t) =
1
E(t)
L
RI(t)
1
Q(t) :
C
Untuk t = 0; diperoleh E(0) = 0; I(0) = 0 dan Q(0) = 0, sehingga I 0 (0) = 0:
Dari rumus I(t) yang ada, diperoleh turunan pertamanya, yaitu
I 0 (t) =
990c1 e
990t
10c2 e
10t
+ (0; 484)(377) sin 377t + (1; 38)(377) cos 377t;
sehingga
I 0 (0) =
990c1
10c2 + (1; 38)(377) = 0:
0
Dari persamaan I(0) = 0 dan I (0) = 0; diperoleh c1 = 0; 526 dan c2 = 0; 042:
Jadi solusi masalah nilai awal (kuat arus dari masalah sirkuit RLC) adalah
I(t) = 0; 526e
990t
0; 042e
10t
0; 484 cos 377t + 1; 38 sin 377t:
|
Example 78 : Masalah Nilai Batas. Medan potensial elektrik di antara dua
bola konsentrik (mempunyai pusat yang sama)
3.5. APLIKASI PERSAMAAN DIFERENSIAL LINIER ORDE DUA
71
Tentukan potensial elektrostatik v = v(r) di antara dua bola konsentrik yang
berjari-jari r1 = 4 cm dan r2 = 8 cm yang masing-masing terjaga pada potensial
v1 = 110 volt dan v2 = 0:
(Catatan: v(r) adalah solusi dari rv 00 + 2v 0 = 0; dengan v 0 = dv=dr:)
Jawab:
Persamaan rv 00 + 2v 0 = 0 dapat diubah menjadi persamaan Euler-Cauchy sebagai berikut:
r2 v 00 + 2rv 0 = 0
Persamaan tambahannya adalah
m2 + m = 0;
yang menghasilkan akar-akar m1 = 0 dan m2 = 1; sehingga solusi umumnya
adalah
v(r) = c1 r0 + c2 r 1 = c1 + c2 =r:
Dari syarat batas v(r1 ) = v(4) = 110 dan v(r2 ) = v(8) = 0; diperoleh hasil
v(4) = c1 + c2 =4 = 110 () 4c1 + c2 = 440
v(8) = c1 + c2 =8 = 0 () 8c1 + c2 = 0:
Dengan eliminasi, diperoleh nilai c1 = 110 dan c2 = 880:
Jadi solusi masalah nilai batasnya yang merupakan potensial elektrostatik di
antara dua bola konsentrik adalah
v(r) =
3.5.1
110 + 880=r volt.
|
Latihan
I. Tentukan arus steady-state ( solusi khusus Ik (t)) dari sirkuit RLC untuk data
berikut ini:
1. R = 2 ohm, L = 1 henry, C = 0:5 farad, E = 50 sin t volts.
2. R = 8 ohm, L = 2 henry, C = 0:1 farad, E = 160 cos 5t volts.
3. R = 4 ohm, L = 1 henry, C = 2:10
4
farad, E = 220 volts.
II. Tentukan arus dalam sirkuit RLC untuk data berikut ini:
4. R = 40 ohm, L = 0:5 henry, C = 1=750 farad, E = 25 cos 100t volts.
5. R = 20 ohm, L = 5 henry, C = 10
2
farad, E = 425 sin 4t volts.
6. R = 10 ohm, L = 0:1 henry, C = 1=340 farad, E = e t (169:9 sin t
160.1t)
III. Selesaikan masalah nilai awal berikut. Asumsikan I dan Q adalah nol jika
t = 0:
7. R = 80 ohms, L = 10 henry, C = 0:004 farad, E = 240:5 sin 10t volts.
8. R = 3 ohms, L = 0:5 henry, C = 0:08 farad, E = 12 cos 5t volts.
9. R = 8 ohms, L = 2 henry, C = 0:1 farad, E = 10 volts.
(a)
72
CHAPTER 3. PERSAMAAN DIFERENSIAL LINIER ORDE KE-N
Chapter 4
Sistem Persamaan
Diferensial
Pada bab-bab terdahulu, telah dibahas metode-metode penyelesaian persamaan
diferensial yang meliputi hanya satu peubah (variabel) saja. Banyak aplikasi
dalam kehidupan sehari-hari yang memerlukan kegunaan dari dua atau lebih
peubah tak bebas, yang masing-masing merupakan fungsi dari peubah bebas
yang tunggal. Hal-hal tersebut di atas, secara alamiah menunjuk kepada suatu
sistem persamaan diferensial biasa secara keseluruhan. Umumnya, peubah bebas tersebut dinyatakan dengan t dan peubah tak bebasnya (yang merupakan
fungsi dari t yang tak diketahui) dengan y1 ; y2 ; :::; yn atau x; y; z; :::
Pembahasan ini akan dibatasi hanya pada suatu sistem dengan banyaknya persamaan adalah sama dengan banyaknya peubah tak bebas (dari fungsi yang tak
diketahui). Sebagai contoh, sistem dari dua persamaan diferensial orde pertama
pada peubah tak bebas y1 dan y2 ; mempunyai bentuk umum:
f1 (t; y1 ; y2 ; y10 ; y20 ) = 0;
f2 (t; y1 ; y2 ; y10 ; y20 ) = 0;
dengan fungsi y1 dan y2 diketahui. Solusi dari sistem ini adalah pasangan
y1 (t); y2 (t) dari fungsi t yang memenuhi kedua persamaan tersebut pada suatu
selang dari t:
4.0.2
Vektor, Matriks
Untuk menyederhanakan formula dan menjelaskan ide-ide pembahasan mengenai sistem linier dari persamaan diferensial, digunakan matriks dan vektor.
Banyak dari sistem linier ini yang terdiri dari dua persamaan di dalam dua
fungsi tak diketahui y1 (t); y2 (t) berbentuk:
y10
y20
= a11 y1 + a12 y2 ;
= a21 y1 + a22 y2 :
Sebagai contoh:
y10
=
y20
=
5y1 + 2y2 ;
1
13y1 + y2 :
2
73
(4.1)
74
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Pada pembahasan selanjutnya nanti, akan dibahas sistem dari n persamaan
dengan n fungsi tak diketahui y1 (t); :::; yn (t) yang berbentuk:
y10
y20
yn0
4.0.3
= a11 y1 + a12 y2 + ::: + a1n yn
= a21 y1 + a22 y2 + ::: + a2n yn
:::::::::::::::::::::::::::::::::::::::::
= an1 y1 + an2 y2 + ::: + ann yn :
(4.2)
Nilai Eigen, vektor Eigen
Misalkan A = [ajk ] adalah matriks. Perhatikan persamaan
A!
x= !
x
(4.3)
x adalah vektor
dengan
adalah skalar (bilangan real atau kompleks) dan !
!
yang masing-masing akan ditentukan. Untuk setiap ; solusinya adalah !
x = 0:
!
!
Skalar seperti pada persamaan (4.3) yang membuat vektor x 6= 0 disebut
nilai eigen dari A dan vektornya disebut vektor eigen dari A yang berhubungan dengan nilai eigen ini. Salah satu arti dari kata ”eigen” dalam bahasa
Jerman, adalah proper . Nilai eigen juga disebut sebagai proper values, nilai
karakteristik atau latent roots (akar laten) oleh beberapa pengarang.
!
!
Persamaan (4.3) dapat ditulis sebagai A!
x
x = 0 atau
(A
I)!
x = 0:
(4.4)
Ini adalah n fungsi aljabar linier dengan x1 ; x2 ; :::; xn ( komponen dari x) yang
!
tak diketahui. Untuk mendapatkan solusi !
x 6= 0 ; koe…sien matriks A
I
harus singular. Dalam bab ini, hanya akan dibahas untuk n = 2; sehingga bila
dinyatakan dalam bentuk matriks, persamaan (4.4) menjadi
a11
a21
a12
a22
x1
x2
=
0
0
;
(4.5)
dengan komponen-komponennya:
(a11
)x1 + a12 x2
a21 x1 + (a22
)x2
= 0
= 0:
(4.6)
A
I singular jika dan hanya jika determinannya sama dengan nol (det (A
I) = 0). Determinan ini, yaitu det (A
I); disebut sebagai determinan
karakteristik dari A (juga untuk n umumnya).
det (A
I)
=
a11
a21
a12
a22
= (a11
)(a22
) a12 a21
2
=
(a11 + a22 ) + a11 a22 a12 a21 = 0:
Persamaan kuadrat di atas disebut sebagai persamaan karakteristik dari A:
Solusinya adalah nilai eigen 1 dan 2 dari A: Jika !
x vektor eigen dari A;
demikian juga k !
x untuk suatu k 6= 0:
Example 79 : Masalah nilai eigen
Tentukan nilai eigen dan vektor eigen dari matriks A =
5
2
2
2
:
4.1. KONSEP DASAR DAN TEORI
75
Jawab:
Persamaan karakteristiknya diperoleh dari :
det (A
I)
5
=
2
=
sehingga menghasilkan nilai eigen
eigennya diperoleh dari persamaan:
( 5
Untuk =
hasilkan:
1
=
2
2
1
=
2
+ 7 + 6 = 0;
1 dan
2
=
)x1 + 2x2 = 0 atau 2x1 + ( 2
6: Sedangkan vektor
)x2 = 0:
1; substitusikan ke dalam persamaan di atas sehingga meng-
4x1 + 2x2
2x1 x2
= 0
= 0:
Karena kedua persamaan tersebut pada dasarnya sama, maka untuk menentukan nilai x1 dan x2 ; dapat diambil sebarang bilangan. Dengan mengambil
x1 = 1 dan x2 = 2 , diperoleh vektor eigen yang pertama, yaitu
1
!
x (1) =
:
2
Untuk = 2 = 6; diperoleh persamaan
x1 + 2x2
2x1 + 4x2
=
=
0
0:
Dengan alasan yang sama seperti di atas, dapat diambil sebarang bilangan untuk
x1 dan x2 nya. Ambil x1 = 2 dan x2 = 1; sehingga diperoleh vektor eigen
2
yang ke dua, yaitu !
x (2) =
:
|
1
4.1
Konsep Dasar dan Teori
Sistem orde I, secara umum dinyatakan dalam bentuk:
y10
y20
yn0
= f1 (t; y1 ; :::; yn );
= f2 (t; y1 ; :::; yn );
:::::::::::::::
= fn (t; y1 ; :::; yn ):
(4.7)
Solusi dari (4.7) pada suatu selang a < t < b adalah himpunan n fungsi yang
diferensiabel (dapat diturunkan) y1 = 1 (t); :::; yn = n (t); pada selang a < t <
b yang memenuhi (4.7). Masalah nilai awal untuk (4.7) terdiri dari (4.7) dan
n kondisi awal yang diberikan:
y1 (t0 ) = K1 ; y2 (t0 ) = K2 ; :::; yn (t0 ) = Kn ;
(4.8)
dengan t0 adalah nilai khusus dari t pada suatu selang dan K1 ; ..., Kn adalah
bilangan yang diketahui.
Theorem 9 : Teorema Keujudan dan Ketunggalan
76
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Perhatikan persamaan (4.7). Misalkan f1 ; :::; fn adalah fungsi kontinu, yang
mempunyai turunan parsial kontinu pada domain R; dari ruang ty1 y2 :::yn yang
memuat titik ( t0 ; K1 ; :::; Kn ): Maka (4.7) mempunyai solusi pada selang t0
< t < t0 + yang memenuhi (4.8), dan solusi ini tunggal.
Persamaan (4.7) disebut sistem linier jika linier di y1 ; :::; yn ; yaitu jika persamaan itu dapat dituliskan dalam bentuk
y10
yn0
= a11 (t)y1 + ::: + a1n (t)yn + g1 (t);
:::::::::::::::::::::::::::
= an1 (t)y1 + ::: + ann (t)yn + gn (t):
(4.9)
Dalam bentuk vektor, persamaan (4.9) menjadi
!
y 0 = A!
y +!
g
(4.10)
dengan
0
1
0
y10
a11
!
y 0 = @ ::: A ; A = @ :::
yn0
an1
1
0
1
0
1
::: a1n
y1
g1
::: ::: A ; !
y = @ ::: A ; !
g = @ ::: A :
::: ann
yn
gn
!
Sistem ini disebut homogen bila !
g = 0 ; sehingga
!
y 0 = A!
y:
(4.11)
!
Jika !
g =
6 0 ; maka persamaan (4.10) disebut nonhomogen.
Theorem 10 : Keujudan dan ketunggalan pada kasus linier
Misalkan ajk dan gj pada persamaan (4.10) adalah fungsi dari t yang kontinu
pada selang terbuka
< t <
yang memuat titik t = t0 : Maka persamaan
(4.10) mempunyai solusi y(t) pada selang yang memenuhi (4.8), dan solusinya
tunggal.
Theorem 11 : Prinsip Superposisi atau Kelinieran
Jika y(1) dan y(2) adalah solusi dari sistem linier homogen (4.11) pada suatu
selang, maka demikian pula dengan kombinasi liniernya, yaitu y = c1 y(1) +
c2 y(2) :
Bukti:
y0
4.2
=
=
=
=
=
[c1 y(1) + c2 y(2) ]0
cy(1)0 + c2 y(2)0
c1 Ay(1) + c2 Ay(2)
A(c1 y(1) + c2 y(2) )
Ay:
Sistem Linier Homogen
Pada sub bab ini kita akan membahas sistem linier homogen
y0 = Ay
(4.12)
Asumsikan matriks A = [ajk ] ukuran nxn adalah konstan. Akan dicari solusi
dari (4.12). Dari bab I yang lalu, diketahui bahwa persamaan y 0 = ky mempunyai solusi y = Cekt : Untuk mencari solusi (4.12) tersebut, digunakan cara
seperti pada persamaan orde I tersebut (bab I).
4.2. SISTEM LINIER HOMOGEN
77
Ambil
y = xe t ;
(4.13)
dan substitusikan persamaan tersebut ke dalam persamaan (4.12), sehingga
diperoleh hasil:
y0 = xe t = Ay = Axe t :
Bagi persamaan tersebut dengan e t ; sehingga
Ax = x
(4.14)
Solusi nontrivial dari (4.12) adalah bentuk (4.13), dengan adalah nilai eigen
dari A dan x adalah vektor eigennya.
Asumsikan A mempunyai basis dari n vektor eigen x(1) ; :::; x(n) yang berkaitan
dengan nilai eigen 1 ; :::; n : Solusi yang berkaitan dengan (4.13) adalah
y(1) = x(1) e
1t
; :::; y(n) = x(n) e
nt
(4.15)
dan mempunyai Wronskian:
(1)
W (y(1) ; :::; y(n) )
1t
x1 e
(1)
x2 e
:::
(1)
xn e
=
1t
1t
(n)
::: x1 e
(n)
::: x2 e
:::
:::
(n)
::: xn e
(1)
nt
nt
(n)
x1
(1)
x2
:::
(1)
xn
1 t+:::+ n t
= e
nt
::: x1
(n)
::: x2
::: :::
(n)
::: xn
:
Pada sisi sebelah kanan, fungsi eksponensial tidak pernah nol dan determinannya tidak nol karena kolomnya adalah vektor eigen bebas linier yang membentuk
basis.
Theorem 12 : Solusi Umum
Jika matriks konstanta A pada sistem (4.12) mempunyai himpunan yang bebas
linier dari n vektor eigen, maka solusi yang berkaitan y(1) ; :::; y(n) pada (4.15)
membentuk basis solusi dari (4.12) dan solusi umumnya adalah:
y = c1 x(1) e
1t
+ ::: + cn x(n) e
nt
:
(4.16)
y10 = 3y1 + y2
y20 = y1 3y2 :
(4.17)
Example 80 : Nilai Eigen Riil Berbeda
Tentukan solusi umum dari sistem linier homogen:
y0 = Ay =
3
1
1
3
y; sehingga
Jawab:
Dengan mensubstitusikan y = xe t dan y0 (t) = xe t dan ’menghilangkan’
fungsi eksponensialnya, diperoleh Ax = x: Persamaan karakteristiknya diperoleh dari:
det(A
I) =
3
1
1
sehingga menghasilkan nilai eigen:
3
1
=
2
=
2 dan
2
+ 6 + 8 = 0;
=
4:
78
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Dari persamaan (A
I) x = 0; diperoleh persamaan:
( 3
)x1 + x2
x1 + ( 3
)x2
= 0;
= 0:
Untuk 1 = 2; diperoleh x1 + x2 = 0 dan x1 x2 = 0 atau x1 = x2 :
Karena kedua persamaan di atas pada dasarnya sama, maka x1 dan x2 mempunyai banyak jawab. Untuk menentukan x1 dan x2 yang memenuhi persamaan
tersebut, dapat diambil sebarang x1 dan x2 ; sehingga darinya dapat ditentukan
1
vektor eigen yang pertama, yaitu x(1) =
:
1
Untuk 2 = 4; diperoleh persamaan x1 + x2 = 0 atau x1 = x2 : Dengan
alasan yang sama seperti di atas, dapat ditentukan vektor eigen yang ke dua,
1
yaitu x(2) =
:
1
Jadi solusi umumnya adalah:
y1
y2
y
=
y
= c1
= c1 y(1) + c2 y(2)
1
1
e
2t
+ c2
1
1
4t
e
:
|
Example 81 : Titik Sadel. Masalah nilai awal
Tentukan solusi umum dari sistem linier homogen berikut ini:
y0 = Ay =
2
1
4
3
y; sehingga
y10 = 2y1 4y2
y20 = y1 3y2 ;
(4.18)
dan solusi khusus yang memenuhi syarat awal: y1 (0) = 3; y2 (0) = 0; atau kalau
3
dalam bentuk vektor dinyatakan dengan y(0) =
:
0
Jawab:
Persamaan karakteristik dari sistem linier tersebut di atas diperoleh dari:
det (A
2
I) =
4
1
3
2
=
+
2 = 0;
sehingga diperoleh nilai eigen: 1 = 1 dan 2 = 2:
Sedangkan vektor eigennya, diperoleh dari persamaan:
(A
I)x =
2
4
1
3
x1
x2
=
0
0
;
yaitu:
(2
x1
)x1 4x2
(3 + )x2
= 0;
= 0:
Untuk = 1; diperoleh persamaan x1 4x2 = 0, sehingga x1 = 4x2 : Karena
kedua persamaan di atas pada dasarnya sama, maka dapat diambil sebarang
x1 dan x2 yang memenuhi persamaan di atas, sehingga diperoleh vektor eigen
4
sebagai berikut: x(1) =
:
1
Dengan cara yang sama, dapat dilakukan untuk = 2; sehingga diperoleh
persamaan 4x1 4x2 = 0 atau x1 x2 = 0 ) x1 = x2 : Dengan alasan yang
4.2. SISTEM LINIER HOMOGEN
79
sama, dapat diambil sebarang x1 dan x2 sehingga diperoleh vektor eigen yang
1
ke dua, yaitu : x(2) =
:
1
Jadi solusi umumnya adalah:
y=
y1
y2
4
1
= c1 y(1) + c2 y(2) = c1
1
1
et + c2
e
2t
Dari syarat awalnya, yaitu y1 (0) = 3 dan y2 (0) = 0 atau kalau dinyatakan secara
3
vektor y(0) =
diperoleh:
0
y(0) = c1
4
1
1
1
+ c2
3
0
=
; sehingga
Dari dua persamaan tersebut diperoleh: c1 = 1 dan c2 =
Jadi solusi khususnya adalah
y=
4
1
1
1
et
e
2t
4c1 + c2 = 3
c1 + c2 = 0:
1:
y1 = 4et e 2t
y2 = et e 2t :
atau
Suatu sistem yang lebih sederhana yang mempunyai titik sadel (pada titik asal
0) adalah
1 0
y 0 = y1
y0 =
y ;sehingga 0 1
(4.19)
0
1
y 2 = y2
Solusi umumnya adalah
y =c1
1
0
et + c2
0
1
e
t
atau
y1 = c1 et
atau y1 y2 = konstanta,
y2 = c2 e t
yang merupakan keluarga hiperbola.
|
Example 82 : Pusat (Nilai Eigen Kompleks)
Tentukan solusi umum dari sistem
0
4
y0 =
1
0
y10 = y2
:
= 4y1
y; sehingga
y20
(4.20)
Jawab:
Persamaan karakteristik dari sistem persamaan diferensial di atas diperoleh dari
determinan karakteristik berikut:
det(A
1
I) =
=
4
sehingga diperoleh nilai eigen: 1 = 2i dan
dari persamaan (A
I)x = 0; yaitu
x1 + x2
4x1
x2
Untuk
1
=
=
2
=
2
+ 4 = 0;
2i: Vektor eigen diperoleh
0;
0:
= 2i; diperoleh persamaan
2ix1 + x2
4x1 2ix2
=
=
0 ) x2 = 2ix1 ;
0 ) 4x1 = 2ix2 :
80
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Karena kedua persamaan tersebut sama, maka untuk menentukan x1 dan x2 ;
dapat diambil sebarang bilangan sehingga x1 dan x2 tersebut memenuhi per1
samaan di atas. Vektor eigen yang diperoleh yaitu: x(1) =
:
2i
Untuk 2 = 2i; diperoleh persamaan
2ix1 + x2
4x1 + 2ix2
= 0 ) x2 = 2ix1 ;
= 0 ) 4x1 = 2ix2 :
Dengan alasan yang sama seperti di atas, dapat dipilih x1 dan x2 sebarang,
1
sehingga diperoleh vektor eigen yang ke dua, yaitu x(2) =
:
2i
Jadi solusi umumnya adalah
y(t)
= c1 y(1) + c2 y(2)
1
= c1
e2it + c2
2i
(4.21)
1
2i
e
2it
;
atau
y1
y2
= c1 e2it + c2 e 2it
= 2i c1 e2it 2i c2 e
2it
Untuk ’menghilangkan’i; perlu diingat bahwa i2 =
kedua persamaan tersebut di atas diperoleh:
y12
1
y2
2
:
1, sehingga dengan mengkuadratkan
= c21 e4it + 2c1 c2 + c22 e
4it
;
2
c21 e4it + 2c1 c2
=
c22 e
4it
:
Dengan menjumlahkan kedua persamaan tersebut, diperoleh:
1
y12 + y22 = 4c1 c2 = konstanta.
4
Karena solusinya merupakan solusi kompleks, maka
e2it = cos 2t + i sin 2t; e
2it
= cos 2t
i sin 2t;
sehingga solusinya berubah menjadi:
y(1)
=
1
2i
1
2i
=
cos 2t + i sin 2t
2i cos 2t 2 sin 2t
e2it =
(cos 2t + i sin 2t)
cos 2t
2 sin 2t
=
(4.22)
sin 2t
2 cos 2t
+i
:
Dengan cara yang sama, diperoleh:
y(2)
=
1
2i
=
cos 2t i sin 2t
2i cos 2t 2 sin 2t
e
2it
=
1
2i
(cos 2t
i sin 2t)
cos 2t
2 sin 2t
=
(4.23)
i
sin 2t
2 cos 2t
sehingga solusi umumnya berubah menjadi:
y
= c1 y(1) + c2 y(2)
cos 2t
= (c1 + c2 )
2 sin 2t
+ i(c1
c2 )
sin 2t
2 cos 2t
:
;
4.2. SISTEM LINIER HOMOGEN
81
Apabila solusi tersebut disubstitusikan ke dalam sistem persamaan pada soal
di atas, maka dapat diketahui bahwa bagian real dan imajiner yang ada di
persamaan [(4.22) dan (4.23)] adalah solusi. Tulis
u=
u1
u2
cos 2t
2 sin 2t
=
v1
v2
; dan v =
sin 2t
2 cos 2t
=
Solusi real ini membentuk basis, karena Wronskiannya tak nol, yaitu
cos 2t
2 sin 2t
W (u; v) =
sin 2t
2 cos 2t
= 2 cos2 2t + 2 sin2 2t = 2;
sehingga solusi umum real dari sistem persamaan diferensialnya adalah
y=
y1
y2
cos 2t
2 sin 2t
= Au+Bv =A
sin 2t
2 cos 2t
+B
;
(4.24)
dengan A = c1 + c2 dan B = i(c1 c2 ): Solusi ini menyatakan elips yang sama
seperti pembahasan sebelumnya, karena
1
y12 + y22 = (A2 + B 2 )(cos2 2t + sin2 2t) = A2 + B 2 = konstanta.
4
| (4.25)
Example 83 : Titik Spiral (Nilai Eigen Kompleks)
Tentukan solusi umum dari
1
1
y0 =
1
1
y10 = y1 + y2
y20 = y1 y2 :
y; sehingga
(4.26)
Jawab:
Persamaan karakteristiknya diperoleh dari determinan karakteristik:
det(A
I) =
1
1
1
1
Nilai eigennya diperoleh dari: 1;2 = 21 (2)
1 + i dan 2 = 1 i:
1 =
Vektor eigennya diperoleh dari persamaan:
1
1
1
x1
x2
1
( 1
)x1 + x2
x1 + ( 1
)x2
Untuk
1
=
=
1
2
2
p
4
+ 2 + 2 = 0:
4(2) =
=
0
0
1
i; sehingga
;
= 0;
= 0:
1 + i; maka
ix1 + x2
x1 ix2
=
=
0 ) x2 = ix1 ;
0 ) x1 = ix2 :
Karena kedua persamaan tersebut sama, maka untuk menentukan x1 dan x2 ;
dapat diambil sebarang bilangan sehingga x1 dan x2 yang diperoleh, memenuhi
kedua persamaan tersebut. Ambil x1 = 1; maka x2 = i; sehingga vektor eigen
1
yang pertama adalah x(1) =
:
i
Untuk 2 = 1 i; maka diperoleh persamaan:
ix1 + x2
x1 + ix2
= 0 ) x2 = ix1 ;
= 0 ) x1 = ix2 :
82
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Dengan alasan yang sama seperti di atas, maka diambil sebarang bilangan untuk
x1 dan x2 yang memenuhi persamaan di atas. Ambil x1 = 1; maka x2 = i;
1
sehingga vektor eigen yang ke dua adalah x(2) =
:
i
Jadi solusi umum dari sistem persamaan linier di atas adalah
= c1 y(1) + c2 y(2) ;
1
= c1
e( 1+i) t + c2
i
y
(4.27)
1
i
e(
1 i) t
:
Solusi persamaan linier di atas dapat dinyatakan dalam bentuk:
y(1)
1
i
=
e(
1+i) t
e t cos t
e t sin t
=
e t (cos t + i sin t)
ie t (cos t + i sin t)
=
t
+i
e
e
=
e t (cos t i sin t)
ie t (cos t i sin t)
t
sin t
cos t
;
dan
y(2)
=
1
i
=
e t cos t
e t sin t
e(
1 i) t
e
e
i
t
t
sin t
cos t
:
Jadi
y
=
=
=
c1 y(1) + c2 y(2)
e t cos t
c1
e t sin t
(c1 + c2 )
e
e
+i
e t cos t
e t sin t
t
t
sin t
cos t
+ i (c1
e t cos t
e t sin t
+ c2
e
e
c2 )
t
t
sin t
cos t
i
e
e
t
t
:
Bagian riil dan imajiner di sebelah kanan persamaan adalah solusi dari (4.26),
sebut saja u dan v; dengan
e t cos t
e t sin t
u=
dan
e
e
v=
t
t
sin t
cos t
:
u dan v membentuk basis, karena Wronskiannya tak nol, yaitu
W (u; v) =
e t cos t
e t sin t
e
e
t
t
sin t
cos t
=e
2t
(cos2 t + sin2 t) = e
2t
:
Solusi umum riil yang berhubungan dengan sistem persamaan linier di atas
adalah:
y
=
= A
y1
y2
= Au + Bv;
e t cos t
e t sin t
+B
(4.28)
e
e
t
t
sin t
cos t
dengan komponen:
y1 = e t (A cos t + B sin t); y2 = e t (B cos t A sin t):
Persamaan di atas menggambarkan suatu gra…k spiral.
;
|
sin t
cos t
4.2. SISTEM LINIER HOMOGEN
4.2.1
83
Tak ada basis dari vektor eigen yang ada
Apabila didapati kasus dengan A tidak punya basis vektor eigen, maka akan
didapatkan solusi bebas linier yang lebih sedikit daripada persamaan (4.12).
Bagaimanakah mencari basis solusi dalam kasus seperti ini ? Misalkan adalah
nilai eigen yang dobel dari A [diperoleh dari det (A I) yang mempunyai
faktor (
)2 ]; dengan hanya diperoleh satu vektor eigen x (bukan dua vektor yang bebas linier seperti biasanya), sehingga hanya didapatkan satu solusi
y(1) = xe t : Solusi ke dua dapat dicari dari persamaan (4.12) dengan jalan
mensubstitusikan:
y(2) = xte t + ue t
(4.29)
ke dalam persamaan (4.12). Turunan pertama dari solusi ke dua tersebut adalah
y(2)0 = xe
t
+ xte
t
+ ue
t
= Ay(2) = Axte
t
+ Aue t :
Dari persamaan di atas diperoleh:
xte t = Axte t ; sehingga x = Ax; dan
xe t + ue t = Aue t ; sehingga x + u = Au:
Jadi
(A I) u = x
Meskipun det (A
u:
(4.30)
I) = 0; persamaan liniernya selalu dapat diselesaikan untuk
Example 84 :
Tentukan solusi umum dari
y0 = Ay =
4
1
1
2
y:
Jawab:
Persamaan karakteristik dari sistem linier di atas diperoleh dari determinan
karakteristik berikut ini, yaitu
det (A
I) =
4
1
1
2
=
2
6 +9=(
3)2 = 0;
yang mempunyai akar dobel = 3:
Vektor eigen diperoleh dari persamaan
(4
)x1 + x2
x1 + (2
)x2
Untuk
= 0;
= 0:
= 3; diperoleh persamaan
x1 + x2
x1 x2
= 0 ) x1 =
= 0 ) x1 =
x2 ;
x2 :
Karena kedua persamaan tersebut sama, maka untuk mencari x1 dan x2 ; dapat
diambil sebarang bilangan.
Ambil x1 = 1; maka x2 = 1; sehingga vektor eigen yang pertama adalah
1
x(1) =
: Dari persamaan (4.30), diperoleh:
1
1
1
(A 3I) u = x
1
u =
1
1
1
; sehingga
u1 + u2 = 1
:
u1 u2 = 1
84
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Karena kedua persamaan tersebut sama, maka kita dapat mengambil sebarang
u1 dan u2 yang memenuhi persamaan tersebut di atas. Dengan mengambil
0
u=
; akan memberikan jawaban untuk sistem persamaan linier di atas
1
sebagai berikut, yaitu:
y
= c1 y(1) + c2 y(2)
1
= c1
e3t + c2
1
1
1
t+
0
1
e3t :
|
Jika A mempunyai tripel nilai eigen dan hanya satu vektor eigen x bebas
linier yang berkaitan dengan nilai eigen tersebut, maka solusi ke dua didapatkan
dari (4.29) dengan u yang memenuhi persamaan (4.30), dan solusi ke tiganya
berbentuk:
1
(4.31)
y(3) = xt2 e t + ute t + ve t ;
2
dengan u memenuhi persamaan (4.30) dan v yang ditentukan dari
(A
I)v = u;
(4.32)
yang selalu dapat diselesaikan.
Apabila A mempunyai tripel nilai eigen dan dua vektor eigen x(1) ; x(2) yang
bebas linier yang berkaitan dengan nilai eigen tersebut, maka ketiga solusi yang
bebas linier tersebut adalah
y(1) = x(1) e t ; y(2) = x(2) e t ; y(3) = xte
t
+ ue
t
(4.33)
dengan x adalah kombinasi linier dari x(1) dan x(2) ; sehingga
(A
I)u = x;
dapat diselesaikan untuk u:
4.2.2
Latihan
Tentukan solusi umum dari sistem persamaan diferensial berikut ini:
y10 = y2
1.
y20 = y1
y10 = 2y1 + 3y2
2.
y20 = 31 y1 + 2y2
y10 = 4y1 6y2
3.
y20 = y1 + y2
Selesaikan masalah nilai awal berikut:
y10 = 2y2
4. y20 = 2y1
y1 (0) = 9; y2 (0) = 15:
y10 = 2y1 + 4y2
5. y20 = y1 + 2y2
y1 (0) = 4; y2 (0) = 4:
y10 = y1 + 4y2
6. y20 = 3y1 2y2
y1 (0) = 3; y2 (0) = 4
(4.34)
4.3. SISTEM LINIER NONHOMOGEN
4.3
85
Sistem Linier Nonhomogen
Suatu sistem linier nonhomogen mempunyai bentuk
y0 = Ay + g
(4.35)
dengan vektor g(t) tidak identik dengan nol. Asumsikan bahwa g(t) dan matriks A(t) ukuran n n; kontinu pada suatu interval J pada sumbu t: Solusi
umum y(h) (t) dari sistem homogen y0 = Ay pada J; dan solusi khusus y (k) (t)
dari persamaan (4.35) pada J; akan membentuk solusi umum sistem persamaan
(4.35) pada J, yaitu
y = y(h) + y(k) ;
(4.36)
karena meliputi setiap solusi dari (4.35) pada J:
4.3.1
Metode Koe…sien Taktentu
Metode ini dapat digunakan jika komponen dari g adalah bilangan bulat t; fungsi
eksponensial atau sinus dan cosinus. Untuk lebih memperjelas pemahaman
pembaca, perhatikan contoh di bawah ini.
Example 85 : Metode koe…sien taktentu
Tentukan solusi umum dari sistem linier nonhomogen:
2
1
y0 = Ay + g =
4
3
2t2 + 10t
t2 + 9t + 3
y+
:
Jawab:
Dengan melihat bentuk g di atas, y(k) dapat diasumsikan dalam bentuk y(k) =
u + vt + wt2 ; dan vektor-vektor u; v, dan w dapat ditentukan.
Dengan substitusi, diperoleh turunan pertama dari solusi khusus y(k) ; yaitu:
y(k)0 = v + 2wt = Au + Avt + Awt2 + g; dengan komponen-komponen:
v1
v2
+
2w1 t
2w2 t
=
2u1
u1
4u2
3u2
+
2v1
v1
2w1
w1
4w2
3w2
t2 +
4v2
3v2
t+
2t2 + 10t
t2 + 9t + 3
:
Dengan menyamakan bagian- t2 pada ke dua sisi, diperoleh:
0 = 2w1 4w2 + 2; 0 = w1 3w2 + 1; sehingga w1 = 1 dan w2 = 0:
Dengan memandang t diperoleh:
2w1 = 2v1 4v2 + 10; 2w2 = v1 3v2 + 9; sehingga v1 = 0 dan v2 = 3:
Dari bagian konstantanya, diperoleh:
v1 = 2u1 4u2 ; v2 = u1 3u2 + 3; sehingga u1 = 0 dan u2 = 0:
Jadi solusi khususnya adalah:
y(k) = u + vt + wt2 =
0
0
+
0
3
t+
1
0
t2 =
t2
3t
:
Dari contoh 2 pada sub bab 4.3, diperoleh solusi umum dari sistem homogennya,
yaitu:
y(h) = c1
4
1
et + c2
1
1
e
2t
;
sehingga solusi umum dari sistem linier nonhomogennya adalah: y = y(h) +
4
1
t2
y(k) = c1
et + c2
e 2t +
:
|
1
1
3t
86
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Example 86 : Modi…kasi dari metode koe…sien taktentu
Tentukan solusi umum dari
3
1
y0 = Ay + g =
1
3
6
2
y+
e
2t
:
Jawab:
Solusi umum dari sistem homogennya (lihat contoh 1 pada sub bab 4.3) adalah:
1
1
y(h) = c1
2t
e
1
1
+ c2
e
4t
:
Karena
= 2 adalah nilai eigen dari A; maka dapat diasumsikan bahwa
y(k) = ute 2t + ve 2t : Dengan substitusi, diperoleh:
y(k)0 = ue 2t 2ute 2t 2ve 2t = Aute 2t + Ave 2t + g:
Dengan menyamakan bagian te 2t pada kedua sisi, diperoleh 2u = Au: Jadi
u adalah vektor eigen dari A yang berkaitan dengan = 2; sehingga uT =
a ( 1 1 ): Dengan menyamakan bagian-bagian yang lain, diperoleh:
u
6
2
2v = Av +
6
2
; karena g =
6
=a
2
dengan komponen-komponennya sebagai berikut:
sehingga Av + 2v = (A + 2I)v = u
v1 + v2
v1 v2
e
1
1
2t
;
6
2
;
= a+6
= a 2:
Karena v1 +v2 = (v1 v2 ); maka agar kedua persamaan tersebut mempunyai
solusi, seharusnya a + 6 = (a 2); sehingga a = 2: Kemudian v1 + v2 = 4
atau v2 = v1 + 4: Misalkan v1 = k; maka v2 = k + 4; sehingga
1
1
v =k
0
4
+
;
0
4
dengan dapat dipilih sebarang k: Misalkan k = 0; maka v =
; sehingga
solusi khusus y(p) adalah
y(k)
= ute
=
2t
2t
+ ve
1
te
1
2
2t
+
0
4
e
2t
:
Jadi solusi umum sistem persamaan nonhomogen tersebut adalah:
y
= y(h) + y(k)
1
= c1
e
1
2t
+ c2
1
1
e
4t
2
1
1
te
2t
+
0
4
e
2t
:
Untuk pilihan k yang lain, akan didapatkan v yang lain pula, seperti misalnya
apabila diambil k = 2; maka vT = ( 2 2 ); sehingga solusi umumnya
menjadi:
y = c1
1
1
e
2t
+ c2
1
1
e
4t
2
1
1
te
2t
+
2
2
e
2t
:
|
4.4. APLIKASI SISTEM PERSAMAAN DIFERENSIAL
4.3.2
87
Latihan
Tentukan solusi umum dari sistem linier nonhomogen berikut ini:
y10 = y2 + 6e2t
1.
y20 = y1 3e2t
y10 = 3y1 + y2 + 3 cos t
2.
y20 = y1 3y2 2 cos t 3 sin t
y10 = y2 5 sin t
3.
y20 = 4y1 + 17 cos t
Selesaikan masalah nilai awal berikut ini:
y10 = 5y2 + 23
y1 (0) = 1; y2 (0) = 2:
4.
y20 = 5y1 + 15t
y10 = 4y1 + 8y2 + 2 cos t 16 sin t
y1 (0) = 0; y2 (0) = 1; 75:
5.
y20 = 6y1 + 2y2 + cos t 14 sin t
y10 = 5y1 + 4y2 5t2 + 6t + 25
y1 (0) = 0; y2 (0) = 0:
6.
y20 = y1 + 2y2 t2 + 2t + 4
4.4
Aplikasi Sistem Persamaan Diferensial
Example 87 :
Diketahui dua buah tangki air T1 dan T2 : Pada awalnya tangki T1 memuat 100
gallon air murni dan tangki T2 memuat 100 gallon air dengan 150 lb pupuk
yang dilarutkan ke dalamnya. Larutan tersebut mengalir melalui tangki-tangki
tersebut pada kecepatan konstan, yaitu 2 gal/min, dan larutan tersebut dijaga
keseragamannya dengan cara mengaduknya. Jika y1 (t) dan y2 (t) menyatakan
banyaknya pupuk dalam tangki T1 dan T2 ; maka kecepatan perubahan y10 (t)
dari y(t) sama dengan aliran yang masuk ke tangki (in‡ow ) per menit dikurangi
aliran yang keluar dari tangki (out‡ow ).per menit. Demikian juga dengan y20 (t)
dari y2 (t): Tentukan banyaknya pupuk y1 (t) dan y2 (t) dalam tangki T1 dan T2
tersebut pada saat t:
Jawab:
I. Tahap Pemodelan
Kecepatan perubahan y10 (t) dari y1 (t) adalah
y10 (t)
= in‡ow/menit - out‡ow/menit
2
2
y2
y1
=
100
100
sedangkan kecepatan perubahan y20 (t) dari y2 (t) adalah
y20 (t)
= in‡ow/menit - out‡ow/menit
2
2
=
y1
y2
100
100
Model matematika dari masalah tersebut adalah
y10
y20
=
0; 02y1 + 0; 02y2
= 0; 02y1 0; 02y2 :
Dalam bentuk matriks dapat dinyatakan sebagai berikut:
Y
0
=
y10
y20
dan
A=
0; 02
0; 02
sehingga sistem persamaan diferensialnya berbentuk:
Y 0 = AY :
0; 02
0; 02
;
88
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
II. Tahap Mencari Solusi Umum
Untuk mencari solusinya, terlebih dulu dicari nilai-nilai eigen yang diperoleh
dari
det (A
I)
0; 02
0; 02
=
0; 02
0; 02
2
()
()
()
()
=
=0
2
( 0; 02
)
(0; 02) = 0
2
+ 0; 04 + 0; 0004 0; 0004 = 0
2
+ 0; 04 = 0
( + 0; 04) = 0
0 atau = 0; 04:
Dari nilai eigen yang diperoleh, kemudian ditentukan vektor eigennya dengan
cara mensubstitusikan nilai eigen tersebut ke dalam persamaan Ax = 0:
a) Untuk nilai eigen = 0; diperoleh vektor eigen sebagai berikut:
0; 02
0; 02
0; 02
x1
0; 02
x2
0; 02x1 + 0; 02x2
0
0
0 =) x1 = x2
=
=
Karena dari persamaan Ax = 0 diperoleh dua persamaan yang sama dalam
x1 dan x2 ; maka kita dapat mengambil sebarang x1 dan x2 : Misalkan diambil
x1 = 1; maka x2 = 1; sehingga diperoleh vektor eigen yang pertama, yaitu
1
x(1) =
:
1
b) Untuk nilai eigen = 0; 04; diperoleh vektor eigen sebagai berikut:
0; 02
0; 02
0; 02
0; 02
x1
x2
0
0
=
0; 02 0; 02
x1
0; 02 0; 02
x2
0; 02x1 + 0; 02x2
0
0
0 =) x1 =
=
=
x2 :
Dengan alasan yang sama seperti di atas, maka dapat diambil sebarang x1 dan
x2 : Misalkan x1 = 1; maka x2 = 1; sehingga diperoleh vektor eigen yang
1
: Dari kedua nilai eigen tersebut selanjutnya dapat
kedua, yaitu x(2) =
1
ditentukan basis solusi umumnya, yaitu
y (1)
= x(1) e
1t
=
y (2)
= x(2) e
2t
=
1
1
1
1
e0:t =
1
1
e
0;04t
:
Jadi solusi umumnya adalah
y
= c1 y (1) + c2 y (2)
1
= c1
+ c2
1
1
1
e
0;04t
:
III. Tahap Mencari Solusi Masalah Nilai Awal
Dari syarat awal yang dikemukakan pada soal, yaitu y1 (0) = 0 dan y2 (0) = 150;
diperoleh
y(0)
=
()
0
150
c1 + c2
c1 c2
= c1
=
1
1
0
150
+ c2
:
1
1
:
4.4. APLIKASI SISTEM PERSAMAAN DIFERENSIAL
89
Dengan eliminasi diperoleh c1 = 75 dan c2 = 75: Jadi solusi masalah nilai
awalnya adalah
1
1
y(t) = 75
75
e 0;04 t ;
1
1
dengan komponen-komponennya sebagai berikut:
y1 (t)
y2 (t)
=
=
75 75e
75 + 75e
0;04t
0;04t
:
Dari dua persamaan tersebut dapat diketahui bahwa gra…knya simetri dan nilai
limitnya menuju ke 75, jika t ! 1: Dengan kata lain, y1 dan y2 konvergen ke
75.
IV. Kesimpulan
Jadi banyaknya pupuk y1 dan y2 di tangki T1 dan T2 pada saat t adalah y1 (t) =
75 75e 0;04t dan y2 (t) = 75 + 75e 0;04t :
|
4.4.1
Latihan
1. Diketahui dua buah tangki air T1 dan T2 ; :yang dihubungkan dengan dua
buah pipa, sehingga air dari tangki T1 dapat mengalir melalui pipa tersebut ke tangki T2 : Demikian pula sebaliknya, air dapat mengalir melalui
pipa dari tangki T2 ke T1 : Pada awalnya tangki T1 memuat 100 gallon
air murni dan tangki T2 memuat 100 gallon air dengan 90 lb (pound)
garam yang dilarutkan ke dalamnya. Larutan tersebut mengalir melalui
tangki-tangki tersebut pada kecepatan konstan, yaitu 4 gal/min, dan larutan tersebut dijaga keseragamannya dengan cara mengaduknya. Tentukan
banyaknya garam y1 (t) dan y2 (t) dalam tangki T1 dan T2 tersebut pada
saat t:
2. Pertanyaan ini berkaitan dengan soal nomor 1. Bagaimana kalau tangki
T1 diganti dengan tangki yang 200 galon? Jelaskan pendapatmu.
3. Pertanyaan ini berkaitan dengan soal nomor 1. Bagaimana kalau ukuran
kedua tangki dikurangki 50 galon? Jelaskan pendapatmu.
90
CHAPTER 4. SISTEM PERSAMAAN DIFERENSIAL
Chapter 5
Solusi Deret Persamaan
Diferensial
5.1
Metode Deret Kuasa
Metode Deret Kuasa adalah suatu metode standar untuk menyelesaikan
persamaan diferensial linier dengan koe…sien peubah. Metode ini akan menghasilkan solusi yang berbentuk deret kuasa. Deret ini dapat digunakan untuk
menghitung nilai-nilai solusi, untuk menjelajahi sifat-sifatnya, dan untuk menurunkan representasi-representasi lain dari solusi tersebut. Pada sub bab ini,
akan dijelaskan dan digambarkan ide-ide dasar dari metode tersebut.
5.1.1
Deret Kuasa
Dari kalkulus yang sudah dipelajari, deret kuasa adalah suatu deret takhingga
yang berbentuk
1
X
x0 )m = a0 + a1 (x
am (x
x0 ) + a2 (x
x0 )2 + :::
(5.1)
m=0
dengan a0 ; a1 ; a2 ; ... adalah konstanta, dan disebut juga sebagai koe…sien dari
deret tersebut. x0 adalah suatu konstanta dan disebut sebagai pusat dari deret,
dan x adalah suatu peubah.
Dalam kasus x0 = 0; akan diperoleh suatu deret kuasa dalam derajat x
1
X
am xm = a0 + a1 x + a2 x2 + :::
m=0
Contoh deret kuasa yang paling dikenal adalah deret Maclaurin
1
1
x
=
1
X
xm = 1 + x + x2 + :::
m=0
(bila jxj < 1; disebut deret geometrik).
x
e
=
cos x =
sin x =
1
X
xm
m=0
1
X
m!
=1+x+
x2
x3
+
+ :::
2!
3!
( 1)m x2m
=1
(2m)!
m=0
1
X
( 1)m x2m+1
=x
(2m + 1)!
m=0
91
x2
x4
+
+ :::
2!
4!
x3
x5
+
+ :::
3!
5!
(5.2)
92
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Ide dari metode deret kuasa sebenarnya sederhana dan alami. Pertama-tama,
dengan menjelaskan prosedur praktik dan menggambarkannya untuk persamaan
yang sederhana yang sudah diketahui, maka dapat dilihat apa yang sedang
terjadi. Perhatikan persamaan diferensial berikut:
y 00 + p(x)y 0 + q(x)y = 0:
(5.3)
Pertama-tama, nyatakan p(x) dan q(x) dengan deret kuasa dalam derajat x
(atau x x0 jika solusi dalam derajat x x0 diinginkan). Seringkali, p(x)
dan q(x) adalah suku banyak (polinom). Selanjutnya, asumsikan solusi dalam
bentuk deret kuasa dengan koe…sien tak diketahui sebagai berikut:
y=
1
X
am xm = a0 + a1 x + a2 x2 + :::
(5.4)
m=0
Dengan diferensiasi, diperoleh
0
y =
1
X
mam xm
1
= a1 + 2a2 x + 3a3 x2 + :::
dan
(5.5)
m=1
00
y =
1
X
m(m
1)am xm
2
= 2a2 + 3:2a3 x + 4:3a4 x2 + :::
(5.6)
m=2
Masukkan deret-deret tersebut ke dalam persamaan (5.3), lalu kelompokkan
bagian-bagian yang memuat derajat x dari x0 ; x1 ; x2 ; dan seterusnya, sehingga
dapat ditentukan koe…sien-koe…sien tak diketahui dalam persamaan (5.4).
Example 88 :
Selesaikan persamaan diferensial berikut: y 0
y = 0:
Jawab:
Tahap pertama, masukkan persamaan (5.4) dan (5.5) ke dalam persamaan diferensial, sehingga diperoleh:
(a1 + 2a2 x + 3a3 x2 + :::) (a0 + a1 x + a2 x2 + :::) = 0
(a1 a0 ) + (2a2 a1 )x + (3a3 a2 )x2 + :::: = 0:
Dengan menyamakan koe…sien dari setiap derajat x dalam persamaan tersebut,
diperoleh:
a1
a0 = 0;
2a2
a1 = 0;
3a3
a2 = 0; dan seterusnya.
Koe…sien-koe…sien a1 ; a2 ; a3 ; dan seterusnya, dapat dinyatakan dalam a0 ; sehingga diperoleh hasil sebagai berikut, yaitu
a1 = a0 ; a2 =
1
1
1
1
a1 = a0 ; a3 = a2 = a0 ; dan seterusnya.
2
2!
3
3!
Dengan demikian, koe…sien dari deret kuasa pada persamaan (5.4) dapat dinyatakan sebagai:
a0
a0
y = a0 + a0 x + x2 + x3 + :::;
2!
3!
yang dapat disederhanakan dalam bentuk yang sudah diketahui, yaitu
y = a0 1 + x +
x2
x3
+
+ ::
2!
3!
= a0 ex :
|
5.1. METODE DERET KUASA
93
Example 89 :
Selesaikan y 0 = 3x2 y:
Jawab:
Dengan memasukkan persamaan (5.4) dan (5.5) ke dalam persamaan diferensial
tersebut, diperoleh hasil:
(a1 + 2a2 x + 3a3 x2 + :::) = 3x2 (a0 + a1 x + a2 x2 + :::)
a1 + 2a2 x + 3a3 x2 + 4a4 x3 + ::: = 3a0 x2 + 3a1 x3 + 3a2 x4 + :::
Dengan membandingkan ke dua sisi dalam persamaan tersebut, diperoleh:
a1 = 0;
2a2 = 0;
3a3 = 3a0 ;
4a4 = 3a1 ;
5a5 = 3a2 ;
6a6 = 3a3 ; :::
Karena a1 = 0; a2 = 0; maka akibatnya a4 = 0; a5 = 0; :::; sehingga
1
1
1
1
a3 = a0 ; a6 = a3 = a0 ; a9 = a6 = a0 ; :::
2
2!
3
3!
Dengan mensubstitusikan hasil tersebut, maka persamaan (5.4) menjadi
1
1
a0 x6 + a0 x9 + :::;
2!
3!
sehingga solusi dari persamaan diferensial tersebut adalah
3
1
1
y = a0 (1 + x3 + x6 + x9 + :::) = a0 ex :
|
2!
3!
Example 90 :
y = a0 + a3 x3 + a6 x6 + a9 x9 + ::: = a0 + a0 x3 +
Selesaikan persamaan diferensial: y 00 + 9y = 0:
Jawab:
Dengan memasukkan persamaan (5.4) dan (5.6) ke dalam persamaan diferensial
tersebut, diperoleh hasil:
(2a2 + 3:2a3 x + 4:3a4 x2 + :::) + 9(a0 + a1 x + a2 x2 + a3 x3 + :::) = 0
(2a2 + 9a0 ) + (3:2a3 + 9a1 )x + (4:3a4 + 9a2 )x2 + ::: = 0
Dengan membandingkan ke dua sisi dalam persamaan tersebut, diperoleh:
2a2 + 9a0
4:3a4 + 9a2
=
=
0; 3:2a3 + 9a1 = 0;
0; 5:4a5 + 9a3 = 0;
::: ;
sehingga
9
9
9
a0 ; a3 =
a1 =
a1 ;
2!
3:2
3!
2
2
9
9
9
a4 =
a2 =
a0 = a0 ;
4:3
4:3:2
4!
9
92
92
a5 =
a3 =
a1 = a1 ; :::
5:4
5:4:3:2
5!
dengan a0 dan a1 konstanta sebarang.
Dengan mensubstitusikan hasil tersebut, persamaan (5.4) menjadi
a2
=
9
9
92
92
a0 x2
a1 x3 + a0 x4 + a1 x5 + :::
2!
3!
4!
5!
32 2 34 4
32 3 34 5
y = a0 (1
x + x
+:::) + a1 (x
x + x
+:::):
2!
4!
3!
5!
Bentuk y yang terakhir ini sudah dikenal sebagai bentuk deret kuasa dari sinus dan cosinus, sehingga solusi persamaan diferensial di atas dapat dituliskan
menjadi
y = a0 cos 3x + a1 sin 3x:
|
y
= a0 + a1 x +
94
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
5.1.2
Latihan
Selesaikan persamaan diferensial berikut ini dengan menggunakan metode deret
kuasa.
1: y 0 = 3y
2: (1 x)y 0 = y
3: y 0 = 2xy
00
00
0
4: y = 4y
5: y = y
6: y 00 + 4y = 0
5.2
Teori Metode Deret Kuasa
5.2.1
Konsep Dasar
Deret kuasa adalah deret tak hingga yang berbentuk
1
X
am (x
x0 )m = a0 + a1 (x
x0 ) + a2 (x
x0 )2 + :::;
(5.7)
m=0
dengan peubah x, pusat x0 ; koe…sien a0 ; a1 ; a2 , ... adalah riil. Jumlah parsial
ke-n dari (5.7) adalah
sn (x) = a0 + a1 (x
x0 ) + a2 (x
x0 )2 + ::: + an (x
x0 )n ;
(5.8)
dengan n = 0; 1; :::. Jika bagian (5.8) dihilangkan dari persamaan (5.7), maka
sisanya adalah
Rn (x) = an+1 (x
x0 )n+1 + an+2 (x
x0 )n+2 + :::.
Rn (x) ini disebut sebagai sisa dari (5.7) setelah bagian an (x
Sebagai contoh, dalam kasus deret geometrik:
(5.9)
x0 )n :
1 + x + x2 + ::: + xn + :::;
diperoleh
s0
s1
s2
= 1;
= 1 + x;
= 1 + x + x2 ;
R0 = x + x2 + x3 + :::
R1 = x2 + x3 + x4 + :::
R2 = x3 + x4 + x5 + :::; dan seterusnya.
Dengan demikian, persamaan (5.7) berkaitan dengan barisan jumlah parsial
s0 (x); s1 (x); s2 (x); :::. Jika untuk suatu x = x1 ; barisan tersebut konvergen,
yaitu
lim sn (x1 ) = s(x1 );
n!1
maka deret (5.7) disebut konvergen pada x = x1 :Bilangan s(x1 ) disebut nilai
atau jumlah dari (5.7) pada x1 ; dan ditulis
s(x1 ) =
1
X
am (x1
x0 )m :
m=0
Maka untuk setiap n berlaku
s(x1 ) = sn (x1 ) + Rn (x1 ):
(5.10)
Jika barisan tersebut menyebar pada x = x1 ; maka deret (5.7) disebut divergen
pada x = x1 :
Dalam kasus kekonvergenan, untuk suatu positif, ada N (yang bergantung
pada ); sedemikian sehingga
jRn (x1 )j = js(x1 )
sn (x1 )j < ;
untuk semua n > N:
(5.11)
Hal ini berarti, bahwa secara geometrik, semua sn (x1 ); dengan n > N; terletak
di antara s(x1 )
dan s(x1 ) + : Prakteknya, hal ini berarti bahwa dalam kasus
kekonvergenan, kita dapat menaksir jumlah s(x1 ) dari (5.7), dengan sn (x1 )
seakurat mungkin yang kita inginkan, dengan mengambil n yang cukup besar.
5.2. TEORI METODE DERET KUASA
95
Selang kekonvergenan. Jari-jari kekonvergenan
1. Deret (5.7) selalu konvergen pada x = x0 ; karena semua bagiannya sama
dengan nol, kecuali bagian pertamanya, yaitu a0 : Dalam kasus khusus, hal
ini mungkin merupakan satu-satunya x di mana (5.7) konvergen.
2. Jika ada nilai x yang lain di mana deret konvergen, nilai-nilai ini membentuk suatu selang, yang disebut selang kekonvergenan. Jika selang
ini berhingga, maka ia mempunyai titik tengah (midpoint) x0 ; sehingga
jx
x0 j < R:
(5.12)
Deret (5.7) konvergen untuk semua x sedemikian sehingga jx x0 j < R; dan
divergen untuk semua x sedemikian sehingga jx x0 j > R: Bilangan R ini
disebut jari-jari kekonvergenan dari (5.7). R ini juga dapat diperoleh dengan
menggunakan rumus lain, yaitu
R = 1= lim
m!1
p
jam j
(5.13)
am+1
am
(5.14)
m
atau
R = 1= lim
m!1
bila limitnya ada dan tidak sama dengan nol. (Jika selang ini tak hingga, maka
(5.7) konvergen hanya pada titik pusat x0 ):
3. Selang kekonvergenan kadang-kadang tak hingga, yaitu (5.7) konvergen
untuk semua x: Sebagai contoh, jika limit dalam (5.13) dan (5.14) nol,
muncul kasus ini. Biasanya orang akan menulis R = 1; untuk mudahnya.
Untuk masing-masing x di mana (5.7) konvergen, mempunyai nilai s(x) yang
tertentu. Dikatakan bahwa (5.7) menyatakan fungsi s(x) dalam selang kekonvergenan, dan ditulis sebagai
s(x) =
1
X
m=0
am (x
x0 )m ;
dengan
jx
x0 j < R:
(5.15)
96
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Example 91 : Kasus 1, kekonvergenan hanya pada pusatnya
Dalam kasus deret
1
X
m!xm = 1 + x + 2x2 + 6x3 + :::;
m=0
diketahui bahwa am = m!; dan dalam (5.14),
am+1
(m + 1)!
=
= m + 1 ! 1;
am
m!
jika m ! 1:
Jadi deret ini konvergen hanya pada pusat x = 0: Deret yang demikian ini tidak
berguna.
Example 92 : Kasus 2, kekonvergenan dalam selang berhingga. Deret Geometrik
Untuk deret geometrik,
1
1
x
=
1
X
xm = 1 + x + x2 + :::;
(jxj < 1)
m=0
diketahui bahwa am = 1; untuk semua m; dan dari persamaan (5.13), diperoleh
R = 1; sehingga deret geometriknya konvergen dan mewakili 1=(1 x); jika
jxj < 1:
Example 93 : Kasus 3, kekonvergenan untuk semua x
Dalam kasus deret
ex =
1
X
xm
m=0
diperoleh am =
1
m! ;
m!
=1+x+
x2
x3
+
+ :::
2!
3!
sehingga dalam (5.14)
1
1=(m + 1)!
am+1
=
! 0;
=
am
1=m!
m+1
jika m ! 1;
sehingga deret tersebut konvergen untuk semua x:
Example 94 : Petunjuk untuk beberapa masalah
Carilah jari-jari kekonvergenan dari deret
1
X
( 1)m 3m
x =1
8m
m=0
x3
x6
+
8
64
x9
+ :::.
512
Jawab:
Deret tersebut merupakan deret yang derajatnya t = x3 ; dengan koe…sien am =
( 1)m =8m ; sehingga dalam (5.14)
am+1
8m
1
= m+1 = :
am
8
8
Jadi R = 8; sehingga deret tersebut konvergen untuk jtj < 8; yaitu jxj < 2:
|
5.2. TEORI METODE DERET KUASA
97
Operasi pada Deret Kuasa
Dalam metode deret kuasa, operasi yang diperbolehkan digunakan adalah menurunkan (di¤ erentiate), menambah dan mengalikan deret kuasa.
1. Menurunkan bagian demi bagian
Deret kuasa dapat diturunkan bagia demi bagian. Jelasnya, jika
y(x) =
1
X
am (x
x0 )m
m=0
konvergen untuk jx x0 j < R; dengan R > 0; maka deret yang diperoleh dengan
menurunkan bagian demi bagian juga konvergen untuk x tersebut dan menyatakan turunan y 0 dari y untuk x tersebut, yaitu
y 0 (x) =
1
X
mam (x
x0 )m
1
;
(jx
x0 j < R) :
; (jx
x0 j < R);
m=1
Dengan cara yang sama, diperoleh y 00 ; yaitu
y 00 (x) =
1
X
m(m
1)am (x
x0 )m
2
m=2
dan seterusnya.
2. Menjumlahkan bagian demi bagian
Dua deret kuasa dapat dijumlahkan bagian demi bagian. Lebih tepatnya, jika
deret
1
1
X
X
am (x x0 )m dan
bm (x x0 )m
(5.16)
m=0
m=0
mempunyai jari-jari kekonvergenan yang positif dan jumlahnya adalah f (x) dan
g(x), maka deret
1
X
(am + bm )(x x0 )m
m=0
konvergen dan menyatakan f (x) + g(x) untuk setiap x, yang terdapat dalam
interior selang kekonvergenan dari setiap deret yang diketahui.
3. Mengalikan bagian demi bagian
Dua deret kuasa dapat dikalikan bagian demi bagian. Lebih tepatnya, misalkan
deret (5.16) mempunyai jari-jari kekonvergenan yang positif dan misalkan f (x)
dan g(x) adalah jumlahnya. Maka deret yang diperoleh dengan mengalikan
setiap bagian dari deret pertama dengan setiap bagian dari deret ke-dua, dan
mengumpulkan derajat yang sama dari x x0 nya, yaitu
1
X
(a0 bm + a1 bm
1
+ ::: + am b0 )(x
x0 )m
m=0
= a0 b0 + (a0 b1 + a1 b0 )(x
x0 ) + (a0 b2 + a1 b1 + a2 + b0 )(x
x0 )2 + :::
konvergen dan menyatakan f (x)g(x) untuk setiap x dalam interior selang kekonvergenan dari setiap deret yang diketahui.
4. Menghilangkan semua koe…sien
Jika suatu deret kuasa mempunyai jari-jari kekonvergenan yang positif dan jumlahnya identik dengan nol sepanjang selang kekonvergenannya, maka setiap koe…sien dari deret tersebut harus nol.
98
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Keujudan Solusi Deret Kuasa
Perhatikan persamaan berikut:
y 00 + p(x)y 0 + q(x)y = r(x):
(5.17)
Jika koe…sien p dan q dan fungsi r pada sisi sebelah kanan persamaan tersebut
mempunyai representasi deret kuasa, maka persamaan (5.17) mempunyai solusi
deret kuasa. Hal yang sama berlaku benar jika e
h; pe; qe dan re dalam persamaan
e
h(x)y 00 + pe(x)y 0 + qe(x)y = re(x)
(5.18)
mempunyai representasi deret kuasa dan e
h(x0 ) 6= 0 (dengan x0 pusat deret).
De…nition 7 : Fungsi Riil Analitik
Fungsi riil f (x) disebut analitik pada titik x = x0 jika dapat direpresentasikan
(dinyatakan) dengan deret kuasa dalam derajat x x0 dengan jari-jari kekonvergenan R > 0:
Theorem 13 : Keujudan Solusi Deret Kuasa
Jika p; q dan r dalam persamaan (5.17) adalah analitik pada x = x0 ; maka
setiap solusi dari persamaan (5.17) adalah analitik pada x = x0 ; dan dapat
dinyatakan dengan deret kuasa dalam derajat x = x0 ; dengan jari-jari kekonvergenan R > 0: Hal yang sama berlaku benar jika e
h; pe; qe dan re dalam persamaan
(5.18) adalah analitik pada x = x0 dan e
h(x0 ) 6= 0 .
5.2.2
Latihan
Carilah solusi deret kuasa dalam derajat x dari persamaan diferensial berikut:
1. y 00
3y 0 + 2y = 0:
2. y 00
4xy 0 + (4x2
2)y = 0:
Tentukan jari-jari kekonvergenan dari deret berikut:
3.
1
P
m=0
5.3
x2m
m!
:
4:
1
P
(m + 1)mxm :
m=0
5:
1
P
m=0
( 32 )m x2m :
Persamaan Legendre, Polinom Legendre Pn (x)
Perhatikan persamaan diferensial berikut
(1
x2 )y 00
2xy 0 + n(n + 1)y = 0:
(5.19)
Persamaan ini disebut persamaan Legendre. Persamaan ini terdapat dalam
berbagai masalah, khususnya dalam masalah nilai batas untuk lengkungan (sphere).
Parameter n dalam persamaan (5.19) adalah bilangan riil yang diketahui. Solusi
dari persamaan (5.19) disebut fungsi Legendre.
Dengan membagi persamaan (5.19) dengan 1 x2 dari y 00 , dapat dilihat bahwa
2x=(1 x2 ) dan n(n + 1)=(1 x2 ) dari persamaan yang baru, adalah analitik
pada x = 0: Oleh sebab itu, berdasarkan Teorema keujudan solusi deret kuasa,
metode deret kuasa dapat diterapkan pada persamaan tersebut.
Substitusikan persamaan
1
X
y=
am xm
(5.20)
m=0
5.3. PERSAMAAN LEGENDRE, POLINOM LEGENDRE PN (X)
99
dan turunan-turunannya ke dalam persamaan (5.19). Misalkan k = n(n + 1),
maka persamaan (5.19) menjadi
2
(1
x )
1
X
m(m
m 2
1)am x
2x
m=2
1
X
m 1
mam x
m=1
1)am xm
m(m
1
X
2
m=2
1
X
m(m
1)am xm
+k
1
X
am xm = 0:
m=0
2
m=2
1
X
mam xm + k
m=1
1
X
am xm = 0:
m=0
(5.21)
Dengan menjabarkan persamaan tersebut di atas, diperoleh
2:1a2 + 3:2a3 x + 4:3a4 x2 + ::: + (s + 2)(s + 1)as+2 xs :::
2:1a2 x2 ::: + s(s 1)as xs + :::
2:1a1 x 2:2a2 x2 ::: 2sas xs :::
+ka0 + ka1 x + ka2 x2 + ::: + kas xs = 0:
Jika (5.20) adalah solusi dari (5.19), maka jumlah koe…sien-koe…sien dari setiap
derajat x harus sama dengan nol. Dengan memasukkan kembali nilai k =
n(n + 1); diperoleh:
untuk koe…sien x0
untuk koe…sien x1
untuk koe…sien x2
:
:
:
2a2 + n(n + 1)a0 = 0;
6a3 + [ 2 + n(n + 1)]a1 = 0;
12a4 + [ 6 + n(n + 1)]a2 = 0;
(5.22)
dan secara umum, jika s = 2; 3; :::; maka untuk koe…sien xs :
(s + 2)(s + 1)as+2 + [ s(s
1)
2s + n(n + 1)]as = 0:
(5.23)
Dengan menyederhanakan bagian [ s(s 1) 2s + n(n + 1)] = (n s)(n + s + 1);
persamaan (5.23) menjadi
(s + 2)(s + 1)as+2 + (n
as+2 =
s)(n + s + 1)as = 0;
(n s)(n + s + 1)
as ;
(s + 2)(s + 1)
s = 0; 1; :::
(5.24)
Persamaan (5.24) ini disebut relasi rekurensi atau rumus rekursi.
Dengan menjabarkan persamaan (5.24), diperoleh
a2
=
a4
=
a3
=
a5
=
n(n + 1)
a0 ;
2!
(n 2)(n + 3)
(n
a2 =
4:3
(n
(n
1)(n + 2)
a1 ;
3!
3)(n + 4)
(n
a3 =
5:4
3)(n
2)n(n + 1)(n + 3)
a0 ;
4!
1)(n + 2)(n + 4)
a1 ;
5!
dan seterusnya, dengan mengambil konstanta a0 dan a1 sebarang.
Dengan memasukkan nilai-nilai dari a tersebut ke dalam persamaan (5.20),
diperoleh
y(x) = a0 y1 (x) + a1 y2 (x);
(5.25)
dengan
y1 (x) = 1
n(n + 1) 2 (n
x +
2!
2)n(n + 1)(n + 3) 4
x
4!
+:::
(5.26)
100
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
dan
y2 (x) = x
(n
1)(n + 2) 3 (n
x +
3!
3)(n
1)(n + 2)(n + 4) 5
x
5!
+::: (5.27)
Deret ini konvergen untuk jxj < 1: Karena persamaan (5.26) hanya memuat x
berderajat genap saja, dan persamaan (5.27) hanya memuat x yang berderajat
ganjil saja, maka perbandingan antara y1 =y2 bukan merupakan suatu konstanta,
sehingga y1 dan y2 tidak proporsional. Dengan demikian, y1 dan y2 adalah
solusi yang bebas linier. Jadi persamaan (5.25) merupakan solusi umum dari
persamaan (5.19), pada selang 1 < x < 1:
5.3.1
Polinom Legendre
Dalam banyak kasus, parameter n dalam persamaan Legendre akan menjadi
bilangan bulat non negatif, sehingga sisi kanan persamaan (5.24)
(n s)(n + s + 1)
as ;
s = 0; 1; :::
(s + 2)(s + 1)
akan sama dengan nol, bila s = n; dan an+2 = 0; an+4 = 0; an+6 = 0; ::: Oleh
sebab itu, jika n genap, maka y1 (x) akan berubah menjadi polinom derajat n
dan jika n ganjil, maka y2 (x) juga akan menjadi polinom derajat n: Polinom
yang demikian ini, bila dikalikan dengan beberapa konstanta, disebut sebagai
polinom Legendre.
Perhatikan rumus as+2 tersebut di atas. Persamaan tersebut dapat dinyatakan
dalam bentuk
as+2 =
(s + 2)(s + 1)
as+2 ;
(n s)(n + s + 1)
as =
(s
n
2):
(5.28)
Dengan memilih an = 1; jika n = 0, dan
(2n)!
1:3:5:::(2n
=
2n (n!)2
n!
an =
1)
;
n = 1; 2; :::
(5.29)
Alasan memilih an yang demikian adalah bahwa semua polinom akan mempunyai nilai 1 jika x = 1:Dari persamaan (5.28) dan (5.29) diperoleh
an
2
n(n 1)
an
2(2n 1)
n(n 1)(2n)!
2(2n 1)2n (n!)2
n(n 1)(2n)(2n 1)(2n 2)!
2(2n 1)2n n(n 1)!n(n 1)(n 2)!
(2n 2)!
:
2n (n 1)!(n 2)!
=
=
=
=
(5.30)
Dengan cara yang sama, diperoleh:
an
4
=
=
(n
2)(n 3)
an 2
4(2n 3)
(2n 4)!
;
2n 2!(n 2)!(n 4)!
dan seterusnya. Secara umum, jika n
an
2m
= ( 1)m
2m
(2n
2n m!(n
0;
2m)!
:
m)!(n 2m)!
(5.31)
5.4. METODE FROBENIUS
101
Hasil solusi dari persamaan diferensial Legendre (5.19) disebut polinom Legendre derajat n dan dinyatakan dengan Pn (x): Dari persamaan (5.31) diperoleh
Pn (x) sebagai berikut:
Pn (x)
=
M
X
( 1)m
m=0
=
(2n)! n
x
2n (n!)2
(2n 2m)!
xn
2n m!(n m)!(n 2m)!
(2n 2)!
2n 1!(n 1)!(n
2)!
xn
2m
2
(5.32)
+ :::
dengan M = a=2 atau (n 1)=2; yang mana saja dari ke dua nilai M tersebut
yang merupakan bilangan bulat.
Contoh untuk fungsi ini adalah
P0 (x)
=
1; P1 (x) = x;
1
1
(3x2 1); P3 (x) = (5x3 3x);
P2 (x) =
2
2
1
1
4
2
P4 (x) =
(35x
30x + 3); P5 (x) = (63x5
8
8
70x3 + 15x);
dan seterusnya.
5.3.2
Latihan
1. Fungsi Legendre untuk n = 0:
Tunjukkan bahwa persamaan (5.26) dengan n = 0; memberikan y1 (x) =
P0 (x) = 1 dan persamaan (5.27) memberikan
y2 (x)
2 3 ( 3)( 1):2:4 5
x3
x5
x +
x + ::: = x +
+
+ :::
3!
5!
3
5
1 1+x
ln
:
2 1 x
= x+
=
Jelaskan hal ini dengan menyelesaikan persamaan (5.19) dengan n = 0;
membentuk z = y 0 dan memisahkan variabel-variabelnya.
2. Fungsi Legendre untuk n = 1:
Tunjukkan bahwa persamaan (5.27) dengan n = 1 memberikan y2 (x) =
P1 (x) = x; dan persamaan (5.26) memberikan
y1 (x)
5.4
=
1
=
1
x2
x4
x6
1
3
5
1
1+x
x ln
:
2
1 x
::: = 1
x(x +
x3
x5
+
+ :::)
3
5
Metode Frobenius
Theorem 14 : Metode Frobenius
Suatu persamaan diferensial yang berbentuk
y 00 +
b(x) 0 c(x)
y + 2 y = 0;
x
x
(5.33)
dengan fungsi b(x) dan c(x) adalah analitik pada x = 0; mempunyai paling
sedikit satu solusi yang dapat dinyatakan dalam bentuk
y(x) = xr
1
X
m=0
am xm = xr (a0 + a1 x + a2 x2 + :::)
(a0 6= 0);
(5.34)
102
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
dengan eksponen r dapat berupa bilangan riil atau kompleks, dan r dipilih
sedemikian sehingga a0 6= 0:
Persamaan diferensial tersebut juga mempunyai solusi ke dua, sedemikan sehingga kedua solusi tersebut bebas linier. Solusi ke dua tersebut hampir sama
dengan solusi pertama pada persamaan (5.34), dengan r berbeda dan koe…sien
yang berbeda pula, atau mungkin akan memuat bagian logaritmik.
Sebagai contoh, persamaan Bessel
y 00 +
1 0
y +
x
x2
v2
y=0
x2
dari bentuk (5.33) dengan b(x) = 1 dan c(x) = x2 v 2 ; analitik pada x = 0;
sehingga teorema 1 (Metode Frobenius) dapat diterapkan. Persamaan ini tidak
dapat dikerjakan secara penuh dengan metode deret kuasa. Serupa dengan
contoh tersebut, persamaan diferensial hipergeometrik juga memerlukan metode
Frobenius dalam penyelesaiannya.
Titik Reguler dan Singuler
Titik reguler dari persamaan diferensial
y 00 + p(x) y 0 + q(x) y = 0;
adalah titik x0 dengan koe…sien p dan q analitik, sehingga metode deret kuasa
dapat diterapkan. Jika titik x0 tidak reguler, maka disebut titik singuler.
Serupa dengan persamaan diferensial tersebut, titik reguler dari
e
h(x) y 00 + pe(x) y 0 + qe(x) y = 0
adalah x0 dengan e
h; pe; qe analitik dan e
h(x0 ) 6= 0 (sehingga persamaan tersebut dapat dibagi dengan e
h; dan mendapatkan bentuk standarnya, seperti pada
persamaan (5.33). Jika x0 tidak reguler, maka disebut singuler.
5.4.1
Persamaan Indisial (Indicial Equation), Menunjukkan
Bentuk Solusi-solusi
Perhatikan persamaan (5.33). Kalikan persamaan tersebut dengan x2 ; sehingga
menghasilkan bentuk
x2 y 00 + x b(x) y 0 + c(x) y = 0:
(5.35)
Dengan menyatakan b(x) dan c(x) dalam bentuk deret kuasa, diperoleh
b(x) = b0 + b1 x + b2 x2 + :::
dan c(x) = c0 + c1 x + c2 x2 + :::
Perhatikan persamaan (5.34). Turunkan persamaan tersebut bagian demi bagian
sehingga diperoleh y 0 dan y 00 sebagai berikut:
y 0 (x) =
1
X
(m + r) am xm+r
1
= xr
1
[r a0 + (r + 1) a1 x + :::]
m=0
y 00 (x)
=
1
X
(m + r)(m + r
m=0
r 2
= x
[r(r
1) am xm+r
2
1) a0 + (r + 1) r a1 x + :::]:
(5.36)
5.4. METODE FROBENIUS
103
Dengan memasukkan semua deret ini ke dalam persamaan (5.35), diperoleh
persamaan
xr [r(r 1) a0 +(r+1) r a1 x+:::]+(b0 +b1 x+b2 x2 )xr [r a0 +(r+1) a1 x+:::] (5.37)
+(c0 + c1 x + c2 x2 + :::)xr (a0 + a1 x + a2 x2 + :::) = 0:
Dengan menyamakan sisi sebelah kiri dan kanan, diperoleh:
untuk koe…sien xr :
[r (r
1) + b0 r + c0 ] a0 = 0:
Dari asumsi a0 6= 0; diperoleh
r (r
1) + b0 r + c0 = 0:
(5.38)
Persamaan ini disebut sebagai persamaan indisial dari persamaan diferensial
(5.33).
Metode ini akan menghasilkan suatu basis solusi-solusi. Salah satu dari dua
solusi tersebut akan selalu berbentuk
r
y(x) = x
1
X
am xm = xr (a0 + a1 x + a2 x2 + :::)
m=0
(a0 6= 0);
dengan r merupakan akar dari persamaan (5.38). Bentuk dari solusi yang lain
akan ditunjukkan dengan persamaan indisial. Berikut ini ada tiga kasus:
1. Akar-akar berbeda, tidak dibedakan oleh suatu bilangan bulat 1, 2, 3, ...
2. Akar dobel.
3. Akar-akar dibedakan oleh bilangan bulat 1, 2, 3, ...
Theorem 15 : Metode Frobenius. Basis solusi. Tiga kasus
Misalkan persamaan diferensial (5.33) memenuhi asumsi-asumsi dalam Teorema 1. Misalkan r1 dan r2 adalah akar-akar dari persamaan indisial. Maka
ada tiga kasus:
Kasus 1: Akar-akar berbeda, tidak dibedakan oleh suatu bilangan
bulat.
y1 (x) = xr1 (a0 + a1 x + a2 x2 + :::)
(5.39)
y2 (x) = xr2 (A0 + A1 x + A2 x2 + :::)
(5.40)
dan
dengan koe…sien-koe…sien yang diperoleh dari (5.37), masing-masing dengan
r = r1 dan r = r2 :
Kasus 2: Akar dobel r = r1 = r2 : Basisnya adalah
y1 (x) = xr (a0 + a1 x + a2 x2 + :::)
[r =
1
(1
2
b0 )]
(5.41)
(mempunyai bentuk umum yang sama seperti sebelumnya) dan
y2 (x) = y1 (x) ln x + xr (A0 + A1 x + A2 x2 + :::)
(x > 0):
(5.42)
Kasus 3: Akar-akarnya dibedakan oleh bilangan bulat. Basisnya adalah
y1 (x) = xr1 (a0 + a1 x + a2 x2 + :::)
(5.43)
(mempunyai bentuk umum yang sama seperti sebelumnya) dan
y2 (x) = ky1 (x) ln x + xr2 (A0 + A1 x + A2 x2 + :::);
di mana akar-akarnya r1
r2 > 0 dan k mungkin bisa nol.
(5.44)
104
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Aplikasi
Example 95 : Persamaan Euler-Cauchy, menggambarkan kasus 1, 2, dan kasus 3 tanpa logaritma
Perhatikan persamaan Euler-Cauchy
x2 y 00 + b0 xy 0 + c0 y = 0
(b0 ; c0 konstanta).
Dengan mensubstitusikan y = xr ; diperoleh persamaan pembantu
r(r
1) + b0 r + c0 = 0;
yang merupakan persamaan indisial. Untuk akar-akar yang berbeda r1 dan r2 ;
diperoleh basis y1 = xr1 dan y2 = xr2 : Untuk akar dobel r; diperoleh basis xr
dan xr ln x:
Example 96 : Ilustrasi kasus 2
Selesaikan persamaan diferensial berikut:
1)y 00 + (3x
x(x
1)y 0 + y = 0:
(5.45)
(Ini persamaan diferensial hipergeometrik yang khusus).
Jawab:
Dengan menuliskan persamaan tersebut dalam bentuk standarnya, yaitu dengan
membagi persamaan tersebut dengan x(x 1); sehingga diperoleh persamaan
baru:
1
(3x 1) 0
y +
y = 0;
y 00 +
x(x 1)
x(x 1)
maka persamaan tersebut memenuhi asumsi Teorema 1. Dengan memasukkan
y dan turunan-turunan y 0 ; y 00 ke dalam persamaan diferensial tersebut, maka
diperoleh
1
X
(m + r)(m + r
1) am xm+r
m=0
1
X
(m + r)(m + r
1) am xm+r
1
+ (5.46)
m=0
3
1
X
(m + r) am xm+r
m=0
1
X
(m + r) am xm+r
m=0
1)
r]a0 = 0;
+
1
X
am xm+1 = 0:
m=0
r 1
Dengan melihat derajat x terendah, yaitu x
…siennya ke nol, maka
[ r(r
1
; dan dengan menyamakan koe-
sehingga r2 = 0:
Maka persamaan indisial ini mempunyai akar dobel r = 0:
Solusi pertama.
Dengan memasukkan nilai ini ke dalam persamaan (5.46), dan menyamakan
jumlah koe…sien dari derajat xs ke nol, maka diperoleh
s(s 1)as (s + 1)sas+1 + 3sas (s + 1)as+1 + as
s as sas s2 as+1 sas+1 + 3sas sas+1 as+1 + as
s2 as + 3sas s2 as+1 3sas+1
s(s + 3)as
as
2
=
=
=
=
=
0;
0;
0;
s(s + 3)as+1 ;
as+1 :
5.4. METODE FROBENIUS
105
Jadi a0 = a1 = a2 = :::; dan dengan memilih a0 = 1; akan diperoleh solusi
y1 (x) =
1
X
xm =
m=0
1
1
(jxj < 1):
x
Solusi Ke-dua.
Solusi ke-dua y2 yang bebas, ditentukan dengan menggunakan metode reduksi
urutan, yaitu dengan mensubstitusikan y2 = u:y1 dan turunan-turunannya ke
dalam persamaan. Dari bentuk standar persamaan diferensial di atas, diperoleh
(3x 1)
p = x(x
1) : Dengan mengintegralkan secara parsial, diperoleh
Z
Z
p dx =
(3x
x(x
1)
dx =
1)
Z
2
x
+
1
1
x
dx =
2 ln(x
1)
ln x:
y2 = u:y1 =
ln x
:
1 x
Jadi
u 0 = U = y1 2 e
R
pdx
=
1
(x 1)2
= ;
2
(x 1) x
x
u = ln x;
y1 dan y2 bebas linier dan membentuk basis pada interval 0 < x < 1:
|
Example 97 : Solusi ke-dua dengan bagian logaritmik
Selesaikan:
x)y 00
(x2
xy 0 + y = 0
(5.47)
Jawab:
Dengan memasukkan y(x) =
y 00 (x) =
1
P
1
P
am xm+r ; y 0 (x) =
m=0
(m + r)(m + r
1
P
(m+r) am xm+r
1
; dan
m=0
1) am xm+r
2
ke dalam persamaan diferensial
m=0
tersebut, diperoleh hasil:
(x2 x)
1
X
(m+r)(m+r 1)am xm+r
2
(m + r)(m + r
m=0
r) am xm+r +
1
P
1
X
(m+r)am xm+r
1
+
m=0
m=0
1
P
x
1
P
1) am xm+r
1
P
1
X
am xm+r = 0:
m=0
1) am xm+r
(m + r)(m + r
1
P
1
m=0
am xm+r = 0:
(m +
m=0
m=0
1
P
[(m+r)(m+r 1) (m+r)+1] am xm+r
m=0
(m+r 1)(m+r) am xm+r
1
=
m=0
0:
1
X
m=0
(m + r
1)2 am xm+r
1
X
1)(m + r) am xm+r
(m + r
1
= 0:
m=0
Perhatikan bagian pertama dari deret tersebut, yaitu
Dengan mengambil m = s; diperoleh hasil
juga bagian ke-dua deret tersebut, yaitu
1
P
s=0
1
P
(m + r
1)2 am xm+r :
m=0
(s + r
(m + r
m=0
1
P
1)2 as xs+r : Perhatikan
1)(m + r) am xm+r
1
:
106
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Dengan mengambil m = s + 1 atau s = m
1; diperoleh hasil
1
P
(s + r)(s +
s= 1
r + 1) as+1 xs+r ; sehingga deret secara keseluruhan menjadi:
1
X
(s + r
2
s+r
1) as x
s=0
1
X
(s + r)(s + r + 1) as+1 xs+r = 0:
(5.48)
s= 1
Dengan menjabarkan deret tersebut, diperoleh hasil:
[(r
1)2 a0 xr + r2 a1 xr+1 + :::]
1) ra0 xr
[(r
Koe…sien dari derajat x terendah (xr
r(r
Karena a0 6= 0; maka
r(r
1
1
+ r(r + 1) a1 xr + :::] = 0:
) adalah
1)a0 = 0:
1) = 0
merupakan persamaan indisial dari persamaan diferensial (5.47). Akar-akar
persamaan indisial tersebut adalah r1 = 1 dan r2 = 0: Karena r1 r2 > 0 (
selisihnya merupakan bilangan bulat), maka mereka termasuk kasus 3.
Solusi Pertama
1
P
Solusi pertama untuk metode Frobenius adalah y1 (x) =
am xm+r1 = a0 xr1 +
m=0
a1 xr1 +1 +a2 xr1 +2 +:::: Karena r1 = 1; maka solusi pertamanya menjadi berbentuk
y1 (x) = a0 x + a1 x2 + a2 x3 + ::::
Untuk mencari koe…sien-koe…sien a0; a1 ; a2 ; ..., masukkan r = r1 = 1 ke dalam
persamaan (5.48), sehingga diperoleh hasil:
1
X
[s2 as
(s + 2)(s + 1)as+1 ] xs+1 = 0:
s=0
Relasi rekurensinya adalah
as+1 =
s2
as ;
(s + 2)(s + 1)
(s = 0; 1; 2; :::):
Untuk s = 0; diperoleh a1 = 0: Untuk s = 1; a2 = 61 a1 = 0; demikian seterusnya
sehingga a3 = 0; a4 = 0; :::Jadi solusi pertama untuk metode Frobenius adalah
y1 (x) = a0 x;
a0 sebarang.
Dengan mengambil a0 = 1; diperoleh solusi pertama y1 (x) = x:
Solusi Ke-dua
Solusi ke-dua dari persamaan diferensial (5.47) dapat dicari dengan menggunakan metode reduksi urutan. Metode ini dapat digunakan bila solusi pertamanya sudah diketahui. Substitusikan y2 = y1 u = xu: Dengan menurunkan y2
sampai turunan ke-dua, diperoleh: y20 = u + xu0 dan y200 = u0 + u0 + xu00 =
2u0 + xu00 : Masukkan y2 dan turunan-turunannya ke dalam persamaan diferensial (5.47), sehingga diperoleh:
(x2
x)(2u0 + xu00 ) x(u + xu0 ) + xu = 0
(x2 x)(2u0 + xu00 ) x2 u0 = 0
(x2 x)xu00 + (x 2)xu0 = 0
x[(x2 x)u00 + (x 2)u0 ] = 0:
5.5. PERSAMAAN BESSEL
107
Karena x 6= 0; maka dengan membagi persamaan tersebut dengan x diperoleh:
(x2
sehingga
A(x
u00
=
u0
1) + Bx =
x
x2
x)u00 + (x
2
=
x
2)u0 = 0;
x 2
A
B
= +
:
x(x 1)
x
x 1
x + 2 =) A = 2;
A+B =
2+B =
1 =) B = 1:Jadi
u00
2
1
=
+
:
0
u
x
x 1
Dengan mengintegralkannya, diperoleh
Z 00
Z
2
1
u
dx
=
+
dx
0
u
x
x 1
ln u0
=
2 ln x + ln(x
ln x2 + ln(x
1) =
1) = ln
x
1
x2
:
Dengan mengeksponensialkan, diperoleh:
u0 =
x
1
x2
=
1
x
1
:
x2
Dengan mengintegralkan dan mengeksponensialkannya lagi, diperoleh:
Z
Z
1
1
0
u dx =
dx
x x2
1
u = ln x + :
x
Jadi solusi ke-duanya menjadi
y2 (x) = y1 u = x(ln x +
1
) = x ln x + 1;
x
dengan y1 dan y2 nya bebas linier, dan y2 mempunyai bagian logaritmik.
5.4.2
1.
2.
3.
4.
5.
6.
7.
|
Latihan
x(1 x)y 00 + 2(1 2x)y 0 2y = 0
xy 00 + 2y 0 + xy = 0
xy 00 + (1 2x)y 0 + (x 1)y = 0
x2 y 00 + 2xy 0 6y = 0
xy 00 + 3y 0 + 4x3 y = 0
8x(1 x)y 00 + (4 14x)y 0 y = 0
4x(1 x)y 00 + y 0 + 8y = 0
5.5
Persamaan Bessel
Salah satu persamaan diferensial yang paling penting dalam matematika terapan
adalah persamaan diferensial Bessel, yang berbentuk
x2 y 00 + xy 0 + (x2
v 2 )y = 0;
(5.49)
dengan v sebuah parameter (bilangan yang diketahui.). Diasumsikan bahwa v
adalah riil dan taknegatif.Persamaan Bessel ini muncul berkaitan dengan medan
listrik, vibrasi, konduksi panas, dan sebagainya.
108
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Persamaan Bessel dapat diselesaikan dengan menggunakan metode Frobenius,
seperti yang sudah diungkapkan pada pembahasan sebelumnya, di mana persamaan tersebut ditulis dalam bentuk standarnya. Dengan mensubstitusikan
deret
1
X
y(x) =
am xm+r ;
a0 6= 0;
m=0
(5.50)
dengan koe…sien taktentu dan turunan-turunannya, yaitu
y 0 (x) =
1
X
(m+r) am xm+r
1
y 00 (x) =
; dan
m=0
1
X
(m+r)(m+r 1) am xm+r
2
m=0
ke dalam persamaan diferensial (5.49), diperoleh
1
X
1) am xm+r +
(m + r)(m + r
m=0
(m + r) am xm+r
m=0
+
1
X
am xm+r+2
v2
m=0
1
X
1
X
pada persamaan tersebut dengan nol,
1) as xs+r +
(s + r)(s + r
1
X
(s + r) as xs+r
s=0
s=0
1
X
+ as xs+r+2
v2
s=0
1
X
as xs+r = 0:
s=0
r
Selanjutnya, koe…sien dari x adalah
1)a0 + ra0
am xm+r = 0:
m=0
m+r
Dengan menyamakan koe…sien dari x
dan bila m = s, diperoleh hasil
r(r
1
X
v 2 a0 = 0;
untuk s = 0:
(5.51)
Koe…sien dari xr+1 adalah
v 2 a1 = 0;
(r + 1)ra1 + (r + 1)a1
untuk s = 1:
(5.52)
Untuk s = 2; 3; 4; :::; koe…sien dari xs+r+2 adalah
(s + r)(s + r
1)as + (s + r)as + as
2
v 2 as = 0:
(5.53)
Dari persamaan (5.51) diperoleh persamaan indisial
(r
v)(r + v) = 0;
dengan akar-akarnya r1 = v (> 0) dan r2 =
(5.54)
v:
Koe…sien Rekurensi dalam kasus r = r1 = v
Untuk r = r1 = v; persamaan (5.52) menjadi
a1 [v 2 + 2v + 1
v 2 ] = 0 =) a1 (2v + 1) = 0;
yang menghasilkan a1 = 0: Persamaan (5.53) dapat ditulis menjadi
(s + r + v)(s + r
v)as + as
2
= 0;
;
5.5. PERSAMAAN BESSEL
109
sehingga untuk r = v; persamaannya menjadi
(s + 2v)sas + as
2
= 0:
(5.55)
Karena a1 = 0 dan v > 0, maka dari persamaan (5.55) diperoleh a3 = 0; a5 =
0; ::: Dengan demikian, persamaan (5.55) hanya akan bergantung pada koe…sien
s yang genap, sehingga dengan mengambil s = 2m; persamaannya akan menjadi
(2m + 2v)2ma2m + a2m
2
= 0;
atau dapat dinyatakan dalam relasi rekurensi:
1
a2m
22 m(m + v)
a2m =
m = 1; 2; :::
2;
(5.56)
Jadi koe…sien a2 ; a4 ; ::: dapat ditentukan, yaitu
a2 =
a0
;
22 (v + 1)
a4 =
a2
a0
= 4
;
22 2(v + 2)
2 2!(v + 1)(v + 2)
dan seterusnya. Secara umum, relasi (5.56) dapat ditulis
a2m =
22m m!(v
( 1)m a0
;
+ 1)(v + 2):::(v + m)
untuk m = 1; 2; :::
(5.57)
Fungsi Bessel Jn (x) untuk bilangan bulat v = n
Nilai bilangan bulat v dinyatakan dengan n; yang merupakan standarnya. Untuk
v = n; relasi (5.57) menjadi
a2m =
22m m!(n
( 1)m a0
;
+ 1)(n + 2):::(n + m)
untuk m = 1; 2; :::;
dengan a0 masih konstanta sebarang, sehingga deret y(x) =
1
P
(5.58)
am xm+r akan
m=0
memuat konstanta sebarang a0 ini. Dengan demikian, a0 dapat dipilih, yang
memungkinkan adalah a0 = 1: Untuk kepraktisan, dipilih
a0 =
1
;
2n n!
karena bila a0 ini disubstitusikan ke dalam relasi (5.58), maka dalam bagian
penyebutnya, yaitu n!(n + 1)(n + 2):::(n + m) = (n + m)!; sehingga relasi pada
(5.58) dapat ditulis dengan
a2m =
( 1)m
;
+ m)!
22m+n m!(n
untuk m = 1; 2; ::::
(5.59)
Dengan koe…sien-koe…sien tersebut dan r1 = v = n; dari persamaan (5.50)
didapatkan solusi khusus dari persamaan diferensial (5.49), yang dinyatakan
dengan Jn (x); dan dituliskan
Jn (x) = xn
1
X
m=0
( 1)m x2m
:
+ m)!
22m+n m!(n
(5.60)
Jn (x) ini disebut sebagai fungsi Bessel jenis pertama yang berderajat n:
Deret ini konvergen untuk semua x:
Example 98 : Fungsi Bessel J0 (x) dan J1 (x)
110
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Untuk n = 0; dari persamaan (5.60) diperoleh fungsi Bessel berderajat nol
J0 (x) =
1
X
( 1)m x2m
=1
22m (m!)2
m=0
x2
x4
+
22 (1!)2
24 (2!)2
x6
+ :::;
26 (3!)2
(5.61)
yang mirip dengan fungsi cosinus. Untuk n = 1; diperoleh fungsi Bessel berderajat satu, yaitu
J1 (x) =
1
X
m=0
( 1)m x2m+1
x
=
+ 1)!
2
x3
22m+1 m!(m
+
23 1!2!
x5
x7
25 2!3!
27 3!4!
+ ::: (5.62)
yang mirip dengan fungsi sinus.
Fungsi Bessel Jv (x) untuk suatu v > 0: Fungsi Gamma
Fungsi Gamma (v) dide…nisikan oleh integral
(v) =
Z1
e t tv
1
dt
(5.63)
0
Dengan mengintegralkan bagian demi bagian, diperoleh
(v + 1) =
Z1
t v
e t dt =
e
t v 1
t 0
+v
Z1
e t tv
1
dt = 0 + v (v)
0
0
Jadi hasil dari integral tersebut adalah relasi dasar
(v + 1) = v (v):
Untuk v = 1;
(1) =
Z1
e t dt =
e
t 1
0
=0
(5.64)
( 1) = 1:
0
Dari hasil tersebut dapat dicari fungsi Gamma untuk v yang lain, yaitu (2) =
1 (1) = 1:1 = 1!; (3) = 2 (2) = 2:1 = 2!; (4) = 3 (3) = 3:2! = 3!; ::: Secara
umum,
(n + 1) = n!
(5.65)
Rumus ini menunjukkan bahwa fungsi Gamma memperumum fungsi faktorial.
Pada pembahasan sebelumnya, diketahui a0 = 2n1n! : Dengan mengganti n! dengan fungsi Gamma, diperoleh a0 = 1=(2n (n + 1)); sehingga untuk suatu v;
a0 =
2v
1
:
(v + 1)
Jadi relasi rekurensinya menjadi
a2m =
22m+v m!(v
( 1)m
:
+ 1)(v + 2):::(v + m) (v + 1)
Perhatikan bahwa
(v + 1) (v + 1) = (v + 2); (v + 2) (v + 2) = (v + 3);
dan seterusnya, sehingga
(v + 1)(v + 2):::(v + m) (v + m) = (v + m + 1):
(5.66)
5.5. PERSAMAAN BESSEL
111
Dengan demikian, rumus relasi rekurensinya menjadi
a2m =
( 1)m
:
(v + m + 1)
(5.67)
22m+v m!
Dari koe…sien-koe…sien ini dan r = r1 = v; serta mensubstitusikannya ke dalam
persamaan (5.50), diperoleh solusi khusus dari persamaan diferensial (5.49), dan
dinyatakan dengan Jv (x); yaitu
v
Jv (x) = x
1
X
m=0
( 1)m x2m
:
(v + m + 1)
(5.68)
22m+v m!
Rumus ini disebut sebagai fungsi Bessel jenis pertama yang berderajat
v: Deret ini konvergen untuk semua x:
Solusi J
v (x)
dari persamaan Bessel
Selain Jv ; untuk solusi umum diperlukan solusi ke dua yang bebas linier. Mengganti v dengan v menyebabkan persamaan (5.68) menjadi
J
v (x)
=x
v
1
X
m=0
22m
( 1)m x2m
:
v m! (m
v + 1)
(5.69)
Karena persamaan Bessel memuat v 2 ; fungsi Jv dan J v adalah solusi dari
persamaan untuk v yang sama. Jika v bukan bilangan bulat, maka Jv dan J v
bebas linier, karena bagian pertama dari persamaan (5.68) dan bagian pertama
dari persamaan (5.69) adalah kelipatan taknol berhingga dari xv dan x v :
Theorem 16 : Solusi Umum persamaan Bessel
Jika v bukan bilangan bulat, solusi umum dari persamaan Bessel untuk semua
x 6= 0 adalah
y(x) = c1 Jv (x) + c2 J v (x):
(5.70)
Bila v bilangan bulat, maka persamaan (5.70) bukan solusi umum karena tidak
bebas linier.
Theorem 17 : Ketakbebasan linier fungsi Bessel Jn dan J
n
Untuk bilangan bulat v = n; fungsi Bessel Jn (x) dan J n (x) tak bebas linier,
karena
J n (x) = ( 1)n Jn (x)
n = 1; 2; :::
(5.71)
112
CHAPTER 5. SOLUSI DERET PERSAMAAN DIFERENSIAL
Chapter 6
Transformasi Laplace
Metode transformasi Laplace adalah suatu metode penyelesaian persamaan diferensial, dan berkaitan dengan masalah nilai awal dan nilai batas. Proses penyelesaiannya dapat dibagi dalam tiga tahap utama, yaitu:
1. Masalah yang berat (sulit) ditransformasikan ke dalam persamaan tambahan (subsidiary equation) yang lebih sederhana.
2. Persamaan yang sederhana tersebut kemudian diselesaikan dengan menggunakan manipulasi aljabar.
3. Penyelesaian persamaan sederhana tersebut selanjutnya ditransformasikan
kembali untuk memperoleh solusi masalah yang diketahui.
Dengan cara tersebut, transformasi Laplace mereduksi masalah penyelesaian
persamaan diferensial menjadi masalah aljabar. Proses ini dibuat menjadi lebih
mudah dengan menggunakan tabel fungsi dan transformasinya, yang perannya
mirip dengan tabel integral dalam kalkulus. Perubahan dari operasi kalkulus
menjadi operasi aljabar pada transformasi disebut kalkulus operasional, yang
sangat penting dalam matematika terapan. Bagi insinyur, metode transformasi
Laplace merupakan metode operasional yang sangat penting. Metode tersebut
sangat berguna khususnya dalam masalah di mana tenaga penggerak mekanik
atau listrik mengalami diskontinuitas, impulsif atau merupakan fungsi periodik
yang sangat rumit, tidak hanya sinus atau cosinus saja. Selain itu, transformasi Laplace juga mempunyai kelebihan yaitu menyelesaikan masalah secara
langsung, masalah nilai awal (tanpa menentukan solusi umum dahulu), dan
persamaan diferensial nonhomogen (tanpa menyelesaikan persamaan homogen
yang terkait terlebih dahulu).
6.1
Transformasi Laplace.
Misalkan f (t) adalah fungsi yang diketahui, yang terde…nisi untuk semua t 0:
Dengan mengalikan f (t) tersebut dengan e st dan mengintegralkannya terhadap
t dari 0 ke tak hingga, maka hasil pengintegralannya (jika ada), merupakan
fungsi dari s; sebut saja F (s); yaitu
F (s) =
Z1
e
st
0
113
f (t) dt:
114
CHAPTER 6. TRANSFORMASI LAPLACE
Fungsi F (s) dari peubah s ini disebut sebagai transformasi Laplace dari
fungsi asal f (t); dan dinyatakan dengan simbol L(f ): Jadi
F (s) = L(f ) =
Z1
st
e
f (t) dt:
(6.1)
0
Perlu diingat, bahwa fungsi asal f bergantung pada t dan fungsi baru F (transformasinya) bergantung pada s: Operasi yang baru saja dijelaskan, yang menghasilkan F (s) dari fungsi yang diketahui f (t) juga disebut transformasi Laplace.
Selanjutnya, fungsi asal f (t) dalam (6.1) disebut transformasi invers atau invers dari F (s); dan dinyatakan dengan L 1 (F ); dan ditulis
1
f (t) = L
(F ):
Notasi: fungsi asal dinyatakan dengan huruf kecil dan transformasinya dinyatakan dengan huruf kapital yang sama, sehingga F (s) menyatakan transformasi
dari f (t); dan Y (s) menyatakan transformasi dari y(t); dan sebagainya.
Example 99 : Transformasi Laplace
Misalkan f (t) = 1; jika t
0: Carilah F (s):
Jawab:
Dari persamaan (6.1) diperoleh pengintegralan
L(f ) = L(1) =
Z1
e
st
dt =
1
e
s
st
1
j=
0
0
1
;
s
(s > 0)
|
Remark 1 :
Selang pengintegralan dalam (6.1) adalah takhingga. Integral yang demikian
disebut integral improper ( tidak murni), dan dengan de…nisi, dievaluasi menurut
aturan
Z1
ZT
st
e
f (t) dt = lim e st f (t) dt:
T !1
0
0
Oleh sebab itu, notasi yang sesuai berarti
Z1
e
st
1
e
s
dt = lim
T !1
0
T
st
1
e
s
= lim
0
T !1
sT
1 0
1
e = ; (s > 0):
s
s
Example 100 : Transformasi Laplace dari fungsi eksponensial
Misalkan f (t) = eat ; jika t
0; dengan a konstanta. Carilah L(f ):
Jawab:
Menurut (6.1),
at
L(e ) =
Z1
e
1
st at
e dt =
a
s
e
0
maka jika s
a > 0;
L(eat ) =
1
s
a
:
|
(s a)t
1
j;
0
6.1. TRANSFORMASI LAPLACE.
115
Theorem 18 : Kelinieran transformasi Laplace
Transformasi Laplace adalah operasi linier, yaitu bahwa untuk suatu fungsi f (t)
dan g(t) yang transformasi Laplacenya ada, dan untuk suatu konstanta a dan
b;
Lfaf (t) + bg(t)g = aLff (t)g + bLfg(t)g:
Example 101 : Aplikasi Teorema 1: Fungsi Hiperbolik
Misalkan f (t) = cosh at = 21 (eat + e
at
); carilah L(f ):
Jawab:
Dari Teorema 1 dan contoh 2 diperoleh
L(cosh at) =
1
1
L(eat ) + L(e
2
2
at
)=
1
2
1
s
dan dengan menyamakan penyebutnya, jika s > a (
L(cosh at) =
1 (s + a) + (s
2
s2 a2
a)
=
a
+
1
s+a
;
0); diperoleh
s
s2
a2
:
Dengan cara yang sama, untuk transformasi dari sinus hiperbolik adalah
L(sinh at) =
dengan s > a
0:
1
L(eat )
2
|
1
L(e
2
at
)=
1
2
1
s
a
1
s+a
=
a
s2
a2
;
116
CHAPTER 6. TRANSFORMASI LAPLACE
Example 102 : Sinus dan Cosinus
Dalam contoh 2, jika diambil a = i!; dengan i =
L(ei!t ) =
1
s
i!
=
p
1; maka akan diperoleh
s
!
s + i!
s + i!
= 2
+i 2
:
= 2
i!)(s + i!)
s + !2
s + !2
s + !2
(s
Sebaliknya, dari Teorema 1 dan ei!t = cos !t + i sin !t; diperoleh
L(ei!t ) = L(cos !t + i sin !t) = L(cos !t) + iL(sin !t):
Dengan menyamakan bagian riil dan imajiner dari kedua persamaan tersebut,
diperoleh transformasi dari cosinus dan sinus sebagai berikut, yaitu
L(cos !t) =
s2
s
;
+ !2
L(sin !t) =
s2
!
:
+ !2
Teorema Pergeseran Pertama: Penggantian s oleh s
formasi
|
a dalam Trans-
Transformasi Laplace mempunyai sifat-sifat umum yang sangat bermanfaat,
yaitu seperti dinyatakan dalam teorema berikut.
Theorem 19 : Teorema Pergeseran Pertama
Jika f (t) mempunyai transformasi F (s)(dengan s > k); maka eat f (t) mempunyai transformasi F (s a) (dengan s a > k): Dalam bentuk rumus,
Lfeat f (t)g = F (s
a);
atau jika diambil inversnya pada kedua sisinya, diperoleh
eat f (t) = L
1
fF (s
a)g:
6.1. TRANSFORMASI LAPLACE.
117
Example 103 Vibrasi Lembab (Damped vibrations)
Dari contoh 4 dan Teorema Pergeseran Pertama, diperoleh rumus yang sangat
bermanfaat, yaitu
s a
;
L(eat cos !t) =
(s a)2 + ! 2
dan
L(eat sin !t) =
(s
!
:
a)2 + ! 2
Untuk a negatif, f (t) ini merupakan vibrasi lembab.
|
Berikut ini adalah tabel singkat dari transformasi yang mendasar. Dari transformasi ini, hampir dapat diperoleh semua transformasi lain yang dibutuhkan
dalam bab ini, melalui penggunaan beberapa teorema umum yang sederhana,
yang akan dibahas pada sesi selanjutnya.
Tabel 6.1 Beberapa fungsi f (t) dan transformasi Laplacenya L(f )
f (t)
L(f )
f (t)
L(f )
s
1
7
cos
!t
1
1
s
s2 +! 2
1
!
2
t
8
sin !t
s2
s2 +! 2
2!
s
2
3
t
9
cosh at
s3
s2 a2
n
t
a
n!
10
sinh at
4
sn+1
s2 a2
(n = 0; 1; 2; :::)
(a+1)
5
ta ; a positif
11 eat cos !t (s sa)2a+!2
sa+1
1
12 eat sin !t (s a)!2 +!2
6
eat
s a
Example 104 : Teorema pergeseran pertama
Dari tabel 6.1 dan Teorema Pergeseran Pertama, diperoleh rumus lain yang
bermanfaat
n!
L(tn eat ) = F (s a) =
:
|
(s a)n+1
Sebagai contoh, L(teat ) = 1=(s
a)2 :
Theorem 20 : Teorema Keujudan Transformasi Laplace
Misalkan f (t) adalah fungsi yang setiap bagiannya kontinu pada setiap selang
berhingga dalam range t 0; dan memenuhi
jf (t)j
Me
kt
;
untuk semua t
0
(6.2)
dan untuk suatu konstanta k dan M: Maka transformasi Laplace dari f (t) ada
untuk semua s > k:
6.1.1
Latihan
A. Tentukan transformasi Laplace dari fungsi berikut:
1. 2t + 6
2: sin
t
3:ea
bt
B. Transformasi Laplace Invers
5.
s 10
s2 s 2
6: s25s25
4: sin (!t + )
118
CHAPTER 6. TRANSFORMASI LAPLACE
Aplikasi dari Teorema Pergeseran Pertama.
C. Carilah transformasi Laplacenya
7:t2 e
3t
8:5e2t sinh 2t
9: sinh t cos t
D. Carilah transformasi inversnya.
3
11: s2 +6s+18
1
10: (s+1)
2
6.2
12: (s+ 1s)2 +1
2
Transformasi dari Turunan dan Integral
Transformasi Laplace adalah metode penyelesaian persamaan diferensial. Idenya
adalah bahwa transformasi Laplace menggantikan operasi kalkulus dengan operasi aljabar pada transformasi. Singkatnya, diferensiasi dari f (t) digantikan
dengan perkalian dari L(f ) dengan s: Pengintegralan f (t) digantikan dengan
pembagian dari L(f ) dengan s:
Theorem 21 : Transformasi Laplace dari turunan f (t)
Misalkan f (t) kontinu untuk semua t 0; memenuhi persamaan (6.2), untuk
suatu k dan M; dan mempunyai turunan f 0 (t) yang perbagiannya kontinu pada
setiap selang berhingga dalam range t
0: Maka transformasi Laplace dari
turunan f 0 (t) ada jika s > k; dan
L(f 0 ) = sL(f )
f (0);
(s > k):
(6.3)
Remark 2 :
Teorema tersebut dapat diperluas, sehingga dengan menggunakan persamaan
(6.3) pada turunan kedua f 00 (t), diperoleh
L(f 00 )
= sL(f 0 )
= s2 L(f )
f 0 (0) = s[sL(f )
sf (0) f 0 (0):
f (0)]
f 0 (0)
(6.4)
Dengan cara yang sama, diperoleh transformasi dari turunan ketiga f 000 (t); yaitu
L(f 000 ) = s3 L(f )
s2 f (0)
sf 0 (0)
f 00 (0):
(6.5)
Selanjutnya, dengan induksi diperoleh perluasan dari Teorema 1.
Theorem 22 : Transformasi Laplace dari turunan orde ke-n
Misalkan f (t) dan turunan-turunannya f 0 (t); f 00 (t); :::; f (n 1) (t) adalah fungsi
yang kontinu untuk semua t 0; memenuhi (6.2), untuk suatu k dan M; dan
misalkan turunan f (n) kontinu perbagian pada setiap selang berhingga dalam
range. Maka transformasi Laplace dari f (n) ada jika s > k dan diberikan oleh
L(f (n) ) = sn L(f )
sn
1
f (0)
sn
2 0
f (0)
:::
f (n
1)
(0):
(6.6)
Example 105 :
Misalkan f (t) = t2 :Turunkan L(f ) dari L(1).
Jawab:
Karena f (0) = 0; f 0 (0) = 0; f 00 (t) = 2; dan L(2) = 2L(1) = 2=s:
Dari (6.4) diperoleh
L(f 00 ) = L(2) =
2
2
= s2 L(f ); sehingga L(f ) = L(t2 ) = 3 :
s
s
|
6.2. TRANSFORMASI DARI TURUNAN DAN INTEGRAL
119
Example 106 :
Turunkan transformasi Laplace dari cos !t:
Jawab:
Misalkan f (t) = cos !t:Maka f 0 (t) =
! sin !t; f 00 (t) =
! 2 cos !t =
f (0) = 1; f 0 (0) = 0: Dengan mengambil transformasi, L(f 00 ) =
persamaan tersebut dan (6.4), diperoleh
! 2 L(f ) = L(f 00 ) = s2 L(f ) sf (0)
s2 L(f ) + ! 2 L(f ) = s ) L(f )[s2 + ! 2 ] = s
s
L(f ) =
= L(cos !t):
s2 + ! 2
! 2 L(f ): Dari
f 0 (0) = s2 L(f )
Dengan cara yang sama dapat diperoleh pula L(sin !t) =
!
s2 +! 2 :
Example 107 :
Misalkan f (t) = sin2 t: Carilah L(f ):
Jawab:
f (0) = 0; f 0 (t) = 2 sin t cos t = sin 2t:
L(sin 2t) =
2
s2 +4
! 2 f (t):
= sL(f ) = sL(sin2 t); sehingga L(sin2 t) =
2
s(s2 +4) :
|
s
120
CHAPTER 6. TRANSFORMASI LAPLACE
Example 108 :
Misalkan f (t) = t sin !t: Carilah L(f ):
Jawab:
f (0) = 0; dan f 0 (t) = sin !t + !t cos !t;
f 00 (t) = 2! cos !t
f 0 (0) = 0:
! 2 t sin !t = 2! cos !t
! 2 f (t):
Dari persamaan (6.4),
L(f 00 )
=
[s2 + ! 2 ]L(f )
=
! 2 L(f (t) = s2 L(f )
2!s
:
2!L(cos !t) = 2
s + !2
2!L(cos !t)
Jadi hasilnya adalah
L(f ) = L(sin !t) =
2!s
(s2
2:
+ !2 )
|
Persamaan Diferensial, Masalah Nilai Awal
Berikut ini akan dibahas bagaimana metode transformasi Laplace menyelesaikan
masalah persamaan diferensial. Perhatikan masalah nilai awal berikut
y 00 + ay 0 + by = r(t);
y(0) = K0 ; y 0 (0) = K1 ;
(6.7)
dengan a dan b konstanta. Dalam hal ini, r(t) adalah input yang diterapkan
pada sistem mekanik, dan y(t) adalah output (respon terhadap sistem). Dalam
transformasi Laplace, ada tiga tahapan yang harus diselesaikan:
Tahap Pertama:
Dengan menulis Y = L(y) dan R = L(r) dan mensubstitusikan persamaan
(6.3) dan (6.4) ke dalam persamaan (6.7), diperoleh persamaan tambahan
(subsidiary equation):
[s2 Y
sy(0)
y 0 (0)] + a[sY
y(0)] + bY = R(s):
Dengan mengumpulkan Y; diperoleh
(s2 + as + b)Y = (s + a)y(0) + y 0 (0) + R(s):
6.2. TRANSFORMASI DARI TURUNAN DAN INTEGRAL
121
Tahap Ke-dua:
Persamaan tambahan tersebut kemudian diselesaikan secara aljabar untuk Y:
Persamaan tersebut selanjutnya dibagi dengan s2 + as + b; dan dengan menggunakan fungsi transfer
Q(s) =
1
;
s2 + as + b
(6.8)
diperoleh solusi
Y (s) = [(s + a)y(0) + y 0 (0)]Q(s) + R(s)Q(s):
(6.9)
Jika y(0) = y 0 (0) = 0; akan memberikan Y = RQ; sehingga Q adalah kuosien
Q=
L(output)
Y
=
:
R
L(input)
Perhatikan bahwa Q hanya bergantung pada a dan b; tidak pada r(t) atau pada
kondisi awal.
Tahap Ke-Tiga:
Persamaan (6.9) direduksi menjadi jumlah bagian-bagian yang inversnya dapat dicari dalam tabel, sehingga solusi y(t) = L 1 (Y ) dari persamaan (6.7)
diperoleh.
Example 109 : Masalah Nilai Awal. Penjelasan Tahap Dasar
Selesaikan:
y 00
y(0) = 1; y 0 (0) = 1:
y = t;
Jawab:
Tahap Pertama:
Dengan menulis Y = L(y); maka berdasarkan persamaan (6.4), transformasi
Laplace untuk turunan ke-dua adalah L(y 00 ) = s2 Y sy(0) y 0 (0); dan L(t) =
1=s2 (lihat tabel); sehingga persamaan tambahan untuk masalah nilai awal
tersebut adalah:
1
:
s2
Dengan syarat awal y(0) = 1; dan y 0 (0) = 1; maka persamaan tambahan
tersebut menjadi
1
(s2 1)Y = (s + 1) + 2 :
s
Tahap Ke-dua:
Dengan mengambil fungsi transfer Q = 1=(s2 1), maka solusi persamaan
tambahan tersebut adalah
[s2 Y
Y (s)
=
=
sy(0)
1
Q=
s2
1
2
s
1
(s + 1)Q +
1
s
1
+
y 0 (0)]
Y =
s+1
1
+ 2 2
2
s
1 s (s
1
:
s2
1)
Keterangan:
1
s2 (s2
1)
=
A
B
A(s2 1) + Bs2
+ 2
=
:
2
s
s
1
s2 (s2 1)
Dengan menyamakan pembilang pada sisi sebelah kiri dengan sisi sebelah kanan
diperoleh:
122
CHAPTER 6. TRANSFORMASI LAPLACE
- untuk koe…sien s2 : A + B = 0 :::(i)
- untuk koe…sien s0 :
A = 1 =) A =
diperoleh B = 1; sehingga
1
s2 (s2
1)
1; akibatnya dari persamaan (i),
1
1
1
+ 2
= 2
s2
s
1
s
1
=
1
s2
Tahap Ke-tiga:
Dari solusi persamaan tambahan, kemudian dicari transformasi inversnya dalam
Tabel 6.1, sehingga diperoleh solusi masalah nilai awal:
y(t)
= L
1
1
(Y ) = L
= et + sinh t
f
1
s
1
|
t:
g+L
1
f
1
s2
1
g
L
1
f
1
g
s2
Example 110 : Perbandingan dengan metode yang biasa
Selesaikan masalah nilai awal berikut:
y 00 + 2y 0 + y = e t ;
y(0) =
1;
y 0 (0) = 1:
Jawab:
I. Penyelesaian dengan transformasi Laplace
Transformasi Laplace dari masalah nilai awal tersebut adalah
L(y 00 ) + 2L(y 0 ) + L(y) = L(e t )
Dari rumus transformasi Laplace untuk turunan-turunan, dan dari tabel (L(e t ) =
1=(s + 1)), diperoleh persamaan tambahan:
[s2 Y
sy(0)
y 0 (0)] + 2[sY
y(0)] + Y =
1
:
s+1
Dengan mengelompokkan Y; dan dari syarat awal y(0) =
samaan tambahan tersebut menjadi
y 0 (0)
2y(0)
=
[s2 + 2s + 1]Y + s
1+2
=
(s + 1)2 Y
=
[s2 + 2s + 1]Y
sy(0)
1; y 0 (0) = 1; per-
1
s+1
1
s+1
s
1+
1
:
s+1
Dengan mengalikan fungsi transfer Q = 1=(s+1)2 dengan persamaan tambahan
tersebut, diperoleh solusi
s 1
1
(s + 1)
1
1
1
+
=
+
=
+
:
(s + 1)2
(s + 1)3
(s + 1)2
(s + 1)3
(s + 1) (s + 1)3
n
o
n
o
1
1
t
1
Transformasi inversnya adalah L 1
=
e
dan
L
=
3
(s+1)
(s+1)
Y (s) =
1 2
t
2t e ;
sehingga solusi masalah nilai awalnya adalah
y(t) = L
Keterangan:
1
(Y (s)) =
e
t
1
+ t2 e
2
t
=
1 2
t
2
1 e t:
|
6.2. TRANSFORMASI DARI TURUNAN DAN INTEGRAL
Dengan memperhatikan L(tn eat ) =
L
1
1
(s + 1)3
n!
(s+a)n+1 ;
1
2
1
=L
123
diperoleh
2!
(s + 1)3
=
1 2 t
t e :
2
II. Penyelesaian dengan metode biasa (metode koe…sien tak tentu)
Perhatikan lagi masalah nilai awal (MNA) pada soal, yaitu:
y 00 + 2y 0 + y = e t ;
y(0) =
1;
y 0 (0) = 1:
Persamaan homogennya adalah
y 00 + 2y 0 + y = 0:
Persamaan karakteristik dari persamaan homogennya:
2
+2 +1 = 0
2
( + 1) = 0 =)
=
1 (dobel)
Solusi dari persamaan homogennya adalah:
t
yh (t) = c1 e
t
+ c2 te
= (c1 + c2 t) e t :
Karena e t dan te t adalah solusi dari persamaan homogennya, maka pilih solusi khusus yk (t) = Ct2 e t ; sehingga turunan-turunannya adalah yk0 = 2Cte t
Ct2 e t = C(2t t2 )e t ; dan yk00 = C[2e t 2te t (2te t t2 e t )] = C[2
4t + t2 ] e t : Dengan mensubstitusikan yk dan turunan-turunannya ke dalam
persamaan diferensial tersebut, diperoleh
C[2
4t + t2 ] e
t
+ 2C(2t
t2 )e
t
+ Ct2 e
t
= e
t
2Ce
t
= e
t
=) C =
1
:
2
Dengan mensubstitusikan nilai C tersebut ke dalam solusi khususnya diperoleh
yk (t) =
1 2 t
t e :
2
Jadi solusi umumnya adalah
y(t) = yh (t) + yk (t) = (c1 + c2 t) e
t
1
+ t2 e t :
2
t
1 2 t
t e :
2
Turunan pertama dari solusi umum y(t) adalah
y 0 (t) = c2 e
t
(c1 + c2 t) e
t
+ te
Dengan memasukkan syarat awalnya, yaitu y(0) =
1; y 0 (0) = c2
y(0) = c1 =
1; dan y 0 (0) = 1; diperoleh
c1 = 1 =) c2 = 0:
Jadi solusi masalah nilai awalnya adalah
y(t) =
Remark 3 :
e
t
1
+ t2 e
2
t
=
1 2
t
2
1 e t:
|
124
CHAPTER 6. TRANSFORMASI LAPLACE
Untuk mengetahui bahwa solusi yang diperoleh adalah benar, yaitu memenuhi
persamaan diferensial dan syarat awalnya, maka substitusikan solusi MNA tersebut dan turunan-turunannya ke dalam persamaan diferensial, dan periksa apakah
hasilnya sama dengan persamaan diferensial nonhomogen tersebut.
Example 111 :
Dari solusi MNA y(t) =
y 0 (t)
= te
y 00 (t)
=
1 2
2t
1 2
t
2
t
(1
1 e t ; diperoleh turunan-turunan
t) e
t
1 e
1+t
t
=
1+t
1 2
t e
2
t
1 2
t e t ; dan
2
1 2
=
t
2t e t :
2
Dengan mensubstitusikan y(t) dan turunan-turunan tersebut ke dalam persamaan diferensialnya, diperoleh
1 2
t
2
t
2t e
+2 1+t
1 2
t e
2
t
+
1 2
t
2
1 e
t
= e t:
Untuk syarat awalnya,
y(0) = 21 :02 1 e 0 = 1 dan y 0 (0) = 1 + 0 12 :02 e 0 = 1:
Jadi benar bahwa solusi MNA adalah y(t) = 12 t2 1 e t :
|
Dengan membandingkan kedua penyelesaian dalam contoh 6 tersebut, dapat
diambil kesimpulan, bahwa metode transformasi Laplace mempunyai kelebihan:
1. Tidak ada penentuan solusi umum dari persamaan homogennya;
2. Tidak ada penentuan nilai untuk konstanta sebarang dalam solusi umumnya.
Transformasi Laplace dari Integral suatu Fungsi
Diferensiasi dan integrasi adalah proses invers. Diferensiasi dari suatu fungsi
berkaitan dengan perkalian dari transformasinya dengan s; maka harapannya
integrasi dari suatu fungsi menghubungkan pembagian dari transformasinya
dengan s; karena pembagian adalah operasi invers dari perkalian.
Theorem 23 : Integrasi dari f (t)
Misalkan F (s) adalah transformasi Laplace dari f (t): Jika f (t) kontinu bagianperbagian dan memenuhi ketaksamaan pada teorema keujudan untuk transformasi Laplace, maka
8t
9
<Z
= 1
L
f ( )d
= F (s)
(s > 0; s > k);
(6.10)
:
; s
0
atau jika kita mengambil transformasi invers pada kedua sisi persamaan tersebut,
Zt
1
F (s) :
(6.11)
f ( )d = L 1
s
0
Example 112 : Aplikasi Teorema 3
Misalkan L(f ) =
1
s(s2 +! 2 ) :
Carilah f (t):
6.2. TRANSFORMASI DARI TURUNAN DAN INTEGRAL
125
Jawab:
Dari Tabel 6.1, diperoleh transformasi invers
1
(s2 + ! 2 )
1
L
=
1
sin !t:
!
Berdasarkan Teorema 3 dan hasil transformasi invers tersebut, diperoleh jawaban
f (t)
= L
1
1
s
1
2
(s + ! 2 )
1
=
!
Zt
sin ! d
0
=
1
!2
t
cos ! j
0
1
= 2 (1
!
cos !t) :
|
Example 113 : Aplikasi lain dari Teorema 3
Dengan cara yang sama seperti pada contoh 7, untuk L(f ) =
f (t) nya.
1
s2 (s2 +! 2 ) ;
carilah
126
CHAPTER 6. TRANSFORMASI LAPLACE
Jawab:
Dari contoh 7, diperoleh transformasi invers
L
1
s(s2
1
+ !2 )
=
1
(1
!2
cos !t) :
Berdasarkan Teorema 3 dan hasil transformasi invers tersebut, diperoleh
f (t)
= L
1
s
1
1
s(s2 + ! 2 )
=
1
!2
Zt
(1
cos ! ) d
0
=
t
1
!2
(
sin ! ) j
0
1
= 2
!
sin !t
!
t
:
|
Masalah Data Pergeseran
Masalah data pergeseran adalah nama singkat untuk masalah nilai awal dengan
kondisi awalnya merujuk pada suatu t = t0 ; bukan t = 0: Dalam hal ini, kondisi
y(0) dan y 0 (0) yang muncul pada pendekatan transformasi Laplace, tidak dapat
langsung digunakan, tetapi harus diproses dalam dua cara.
1. Metode solusi pertama. Carilah solusi umum dengan transformasi
Laplace dan setelah itu, carilah solusi dari masalah seperti pada metode klasik.
2. Metode solusi ke-dua. Dengan mengambil t = e
t + t0 ; sehingga t = t0 ;
memberikan hasil e
t = 0: Dengan demikian, transformasi Laplace baru dapat
diterapkan.
Example 114 :
Dengan menggunakan metode pada masalah data pergeseran tersebut di atas,
akan diselesaikan masalah nilai awal berikut:
y 00 + y = 2t;
y
1
4
=
1
;
2
y0
1
4
=2
p
2:
Jawab:
Dari masalah nilai awal tersebut, diketahui t0 = 14 ; sehingga t = e
t + 14 : Dengan
1
demikian, untuk t = t0 = 4 ; menyebabkan e
t = 0; sehingga masalah nilai awal
tersebut berubah menjadi
1
ye00 + ye = 2(e
t+
);
4
y (0) =
1
;
2
y 0 (0) = 2
p
2:
Tahap I: Membentuk persamaan tambahan
Dengan menuliskan Ye = L(e
y ); maka dengan rumus transformasi Laplace untuk
turunan-turunan, yaitu
L (e
y 00 ) = s2 Ye
dan dari tabel,
1
L 2(e
t+
)
4
se
y (0)
=
ye0 (0)
2
=2
+
s2
s
diperoleh persamaan tambahan sebagai berikut:
h
s2 Ye
se
y (0)
i
2
=2
ye0 (0) + Ye = 2 +
:
s
s
6.2. TRANSFORMASI DARI TURUNAN DAN INTEGRAL
127
Tahap II: Solusi dari persamaan tambahan
Secara aljabar, persamaan tambahan tersebut dapat diselesaikan, yaitu
1
s
2
s2 + 1 Ye
p
2
2
=2
2
+
s2
s
2
=2 1
+
+
s+ 2
s2
s
2
=
s2 + 1 Ye
=
p
2 ;
sehingga solusi persamaan tambahannya menjadi
Ye =
p
2
2
=2
s
+
+
+ 2
:
2
2
2
2
s (s + 1) s(s + 1) 2(s + 1)
(s + 1)
2
Dari contoh 7 dan 8 sebelumnya, diperoleh solusi
ye =
=
Karena e
t=t
2 e
t
1
2e
t+
2
1
4
sin e
t +
p
cos e
t +
1
2 sin e
t:
; dan cos 14
y(t)
1
2
= sin 14
1
4
=
+
1
2
p
2 t
=
2t
p
2 sin t cos
=
2t
p
2
=
2t
p
2 sin e
t
2; maka
p
1
2
=
1
cos e
t+ 2
2
1
4
1p
2 sin t
2
sin t + cos t:
1
4
1
cos t sin
4
1p
2 cos t
2
2 sin t
Jadi solusi masalah data pergeseran tersebut adalah
y(t) = 2t
6.2.1
sin t + cos t:
|
Latihan
I. Selesaikan masalah nilai awal berikut dengan transformasi Laplace.
1. y 0 + 3y = 10 sin t;
2. y 00
4y 0 + 3y = 6t
3. y 00 + 2y 0
3y = 6e
y(0) = 0
8;
2t
;
y(0) = 0; y 0 (0) = 0
y(0) = 2; y 0 (0) =
14:
II. Diketahui L(f ); carilah f (t): Gunakan transformasi invers dan integrasi.
4.
1
s2 +4s
5.
1
s3 s
128
CHAPTER 6. TRANSFORMASI LAPLACE
Appendix A
Abjad Yunani dan
Rumus-rumus Trigonometri
A.1
A
B
E
Z
H
I
K
M
A.2
Abjad Yunani
alpha
beta
gamma
delta
epsilon
zeta
eta
theta
iota
kappa
lambda
mu
N
O
o
P
T
X
!
nu
xi
omicron
pi
rho
sigma
tau
upsilon
phi
chi
psi
omega
Rumus-rumus Trigonometri
Hukum Cosinus
Jika A, B dan C adalah sudut-sudut dalam dari suatu segitiga dan a; b dan c
adalah sisi-sisi yang berseberangan dengan sudut-sudut tersebut, maka
a2 = b2 + c2
2bc cos A:
Identitas Pythagoras
sin2 x + cos2 x = 1
1 + tan2 x = sec2 x
cot2 x + 1 = csc2 x
Rumus-rumus Reduksi
sin ( x) = sin x
cos ( x) = cos x
tan ( x) = tan x
sin 2 + x = cos x
tan 2 + x = cot x
tan (x
) = tan x
129
130APPENDIX A. ABJAD YUNANI DAN RUMUS-RUMUS TRIGONOMETRI
Rumus-rumus Tambahan
sin (x
cos (x
tan (x
y) = sin x cos y cos x sin y
y) = cos x cos y sin x sin y
tan x tan y
y) =
1 tan x tan y
Rumus Sudut Ganda
sin 2x = 2 sin x cos x
cos 2x = cos2 x sin2 x = 2 cos2 x
1=1
2 sin2 x
Rumus Setengah Sudut
sin2
x
1
=
2
cos x
;
2
cos2
1 + cos x
x
=
2
2
Jumlah dan Perkalian
sin x + sin y
sin x
sin y
cos x + cos y
cos x
cos y
x+y
x y
cos
2
2
x y
x+y
= 2 sin
cos
2
2
x+y
x y
= 2 cos
cos
2
2
x+y
x y
= 2 sin
cos
2
2
=
2 sin
The appendix fragment is used only once. Subsequent appendices can be created
using the Chapter Section/Body Tag.
Appendix B
Rumus-rumus Turunan dan
Integral
B.1
Tabel Turunan
1. Dx (un ) = nun
1
Dx u
2. Dx (u + v) = Dx u + Dx v
3. Dx (uv) = uDx v + vDx u
4. Dx
u
v
=
vDx u uDx v
v2
5. Dx (eu ) = eu Dx u
6. Dx (au ) = au ln a Dx u
7. Dx (ln u) =
1
u
Dx u
8. Dx (sin u) = cos u Dx u
9. Dx (cos u) =
sin u Dx u
10. Dx (tan u) = sec2 u Dx u
csc2 u Dx u
11. Dx (cot u) =
12. Dx (sec u) = sec u tan u Dx u
13. Dx (csc u) =
csc u cot u Dx u
14. Dx (sin
1
x) =
p 1
1 u2
Dx u
15. Dx (cos
1
x) =
p
1
1 u2
Dx u
16. Dx (tan
1
x) =
1
1+u2
Dx u
17. Dx (cot
1
x) =
1
1+u2
Dx u
18. Dx (sec
1
x) =
p1
juj u2 1
Dx u
19. Dx (csc
1
x) =
p1
juj u2 1
Dx u
20. Dx (sinh u) = cosh u Dx u
21. Dx (sinh u) = cosh u Dx u
131
132
APPENDIX B. RUMUS-RUMUS TURUNAN DAN INTEGRAL
22. Dx (cosh u) = sinh u Dx u
23. Dx (tanh u) = sec h2 u Dx u
csc h2 u Dx u
24. Dx (coth u) =
25. Dx (sec h u) =
sec h u tanh u Dx u
26. Dx (csc h u) =
csc h u coth u Dx u
B.2
Integral Trigonometri
Yang berbentuk
1:
2:
Z
Z
p
p
a2
u2
du
2au u2
p
p
a2
Yang berbentuk a2
Z
du
a2 + u2
Z
du
2:
2
a
u2
Z
du
3:
2
u
a2
1:
=
=
=
=
sin
1
=
cos
1
a2 + u2 dan
du
+ u2
Z
du
2: p
2
u
a2
1:
p
u2 , dan
du
a2
Yang berbentuk
Z
p
p
2au
sinh
1
=
cosh
1
u2 dan u2
u
+ c; jika u2 < a2 ; a > 0:
a
r
u
u
+ c = 2 sin 1
+ c:
1
a
2a
u2
=
u2
a2
p
u
+ c = ln u + a2 + u2 :
a
p
u
+ c = ln u + u2 a2 :
a
a2
u
1
tan 1
+ c; jika a_ > 0:
a
a
u
1
a+u
1
tanh 1
+c=
ln
+ c; jika u2 < a2 :
a
a
2a
a u
1
u
1
u a
coth 1
+c=
ln
+ c; jika u2 > a2 :
a
a
2a
u+a
Yang Berbentuk Trigonometri
1.
2.
3.
4.
R
R
R
R
sin u du =
cos u + c:
cos u du = sin u + c:
tan udu =
ln cos u + c = ln sec u + c:
cot udu = ln sin u + c =
ln csc u + c:
B.2. INTEGRAL TRIGONOMETRI
5.
6.
7.
8.
9.
10.
11.
12.
13.
R
R
R
R
R
R
R
R
R
133
sec udu = ln(sec u + tan u) + c = ln tan
csc udu =
u
2
+
u
2
ln (csc u + cot u) + c = ln tan
4
+ c:
sec2 udu = tan u + c:
csc2 udu =
cot u + c:
sec u tan udu = sec u + c:
csc u cot udu =
csc u + c:
sin2 udu =
1
2
(u
sin u cos u) + c = 21 u
cos2 udu =
1
2
(u + sin u cos u) + c = 21 u +
tan2 udu = tan u
1
4
sin 2u + c:
1
4
sin 2u + c:
u + c:
Yang Berbentuk Invers Trigonometri
1.
2.
3.
R
R
R
sin
1
udu = u sin
1
cos
1
udu = u cos
tan
1
udu = u tan
p
u
1
u
1
1
u2 + c
p
u2 + c
1
2
u
1
ln 1 + u2 + c:
Yang Berbentuk Eksponensial dan Logaritmik
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
R
R
R
R
R
R
R
R
R
R
+ c:
eu du = eu + c
au du =
au
ln a
+c
ueu du = eu (u
1) + c
un eu du = un eu
eu
uu du
=
n
eu
(n 1)un
1
R
un
+
ln udu = u ln u
u+c
un ln udu = un+1
h
du
u ln u
ln u
n+1
1 u
e du
1
n 1
R
eu
uu 1 du
1
(n+1)2
i
+c
= ln(ln u) + c
eau sin nudu =
eau (a sin nu n cos nu)
a2 +n2
+c
eau cos nudu =
eau (a cos nu+n sin nu)
a2 +n2
+c
134
APPENDIX B. RUMUS-RUMUS TURUNAN DAN INTEGRAL
Yang Berbentuk Hiperbolik
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
sinh udu = cosh u + c
cosh udu = sinh u + c
tanh udu = ln cosh u + c
coth udu = ln sinh u + c
sec hudu = tan
1
(sinh u) + c
csc hudu = ln tanh 12 u + c
sec h2 udu = tanh u + c
csc h2 udu =
coth u + c
sec hu tanh udu =
sec hu + c
csc hu coth udu =
csc hu + c
sinh2 udu =
1
4
sinh 2u
cosh2 udu =
1
4
sinh 2u + 21 u + c
1
2u
+c
u sinh udu = u cosh u
sinh u + c
u cosh udu = u sinh u
cosh u + c
eau sinh nudu =
eau (a sinh nu n cosh nu)
a2 n2
+c
eau cosh nudu =
eau (a cosh nu n sinh nu)
a2 n2
+c
Daftar Pustaka
1. Edward Jr., C. H. & Penney, David E. (1993). Elementary Di¤ erential
Equations with Boundary Value Problems, Third Edition. New Jersey:
Prentice-Hall, Inc.
2. Finan, M.B. (2012). A First Course in Elementary Di¤erential Equations.
[Online]. Tersedia: http://math.utoledo.edu/~melbialy/classes/Elem-DE/Finandi¤ q1book.pdf. [16 Februari 2012]
3. Kreyszig, E. (1999). Advanced Engineering Mathematics, 8th Edition.
New York: John Wiley & Sons, Inc.
4. Ross, Shepley L. (1974). Di¤ erential Equations. New York: John Wiley
& Sons, Inc.
5. Simmons, George F. (1991). Di¤ erential Equations with Applications and
Historical Notes. Second Edition. New York: McGraw-Hill, Inc.
135