File

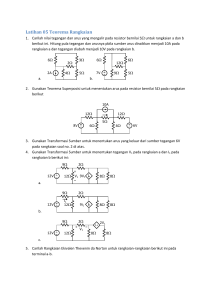
Teorema Superposisi
Teorema ini hanya berlaku untuk rangkaian yang bersifat linier. Rangkaian linier adalah suatu
rangkaian dimana persamaan yang muncul akan terpenuhi jika y = kx, dimana k = konstanta dan
x = variable.
Dalam setiap rangkaian linier dengan beberapa buah sumber tegangan atau sumber arus,
perhitungannya dapat dilakukan dengan cara:
“Menjumlahkan secara aljabar tegangan atau arus yang disebabkan oleh tiap sumber bebas
yang bekerja sendiri, dengan semua sumber tegangan atau arus bebas lainnya yang diganti
dengan tahanan dalamnya.”
Pengertian dari teorema dia atas bahwa jika terdapat n buah sumber bebas, maka dengan
teorema superposisi itu berarti sama dengan n buah keadaan rangkaian yang akan di analisisis,
dimana nantinya n buah keadaan tersebut akan dijumlahkan. Jika terdapat beberapa buah
sumber tak bebas, maka tetap saja teorema superposisi menghitung n buah keadaan dari n
buah sumber bebasnya.
Rangkaian linier tentu tidak terlepas dari gabungan rangkaian yang mempunyai sumber bebas,
sumber tak bebas linier ( sumber tak bebas arus/tegangan tak bebas sebanding dengan pangkat
satu dari tegangan/arus lain, atu sebanding dengan jumlah pangkat satu besaran – besaran
tersebut), dan elemen resistor, induktor, serta kapasitor.
Dalam setiap rangkaian listrik, tegangan dan arus pada suatu unsur merupakan akibat yang
ditimbulkan oleh sumber yang dikenakannya. Jika suatu rangkaian mempunyai beberapa
sumber, setiap tegangan dan arus pada unsur – unsurnya dapat dipandang sebagai jumlah
beberapa komponen dimana masing – masing komponen disebabkan oleh sebuah sumber.
Prinsip superposisi, jika diterapkan pada suatu rangkaian konstant, menyatakan bahwa arus
atau tegangan di setiap cabang yang dihasilkan oleh beberapa sumber yang dikenakan
serentak adalah jumlah aljabar arus atau tegangan yang dihasilkan pada cabang itu oleh masing
– masing sumber itu secara tersendiri. Prinsip ini berdasarkan kenyataan bahwa arus dalam
setiap resistansi berbanding lurus dengan tegangannya.
Langkah – langkah penyelesaian dengan teorema Superposisi:
 Berpatokan pada sumber arus
 Menentukan arah arus
 Menghitug besar arus pada masing – masing beban
Soal
Menghitung arus I dengan teorema superposisi
10 Ω
20 Ω
10 Ω
DC
1 A
Jawaban:
Pada saat sumber tegangan aktif/bekerja maka sumber arus tidak aktif ( diganti dengan
tahanan dalamnya yaitu tak hingga atau rangkaian open circuit):
Maka : i1 =
20
=1A
10 + 10
10 Ω
20 Ω
10 Ω
DC
Pada sumber arus aktif/ bekerja maka sumber tegangan tidak aktif ( diganti dengan tahanan
dalamnya yaitu nol atau rangkaian short circuit):
10 Ω
10 Ω
I2 =
10
1 = - 0,5 A
10 + 10
Sehingga :
I = i1 + i2 = 1 – 0,5 = 0,5 A
1A
TEOREMA SUPERPOSISI
 BERPATOKAN PADA SUMBER
 MENENTUKAN ARAH ARUS
 MENGHITUNG BESAR ARUS PADA MASING-MASING BEBAN
Berpatokan pada E1
Menentukan arah arus
Diketahui:
E1=28v
E2=7V
R1=4Ω
R2=2Ω
R3=1Ω
Menghitung besar arus pada masing-masing beban
I11=
RT= R1+
=4 +
= Ω
I11=
=
= 6A
I2
1=
=
=2A
I31=
=
I11
6A
I11
6A
=4A
Berpatokan pada E2
Menentukan arus
I32=
RT= R3+
=1 +
= Ω
I32=
=
= 3A
I2
2=
=
I32
3A
=2A
I1
2=
=
I32
3A
=1A
Menghitung jumlah arus
I1
I2
I3
E1
6A
2A
4A
E2
1A
2A
3A
5A
4A
1A
Teorema Thevenin
Pada teorema ini berlaku bahwa:
Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri dari satu buah
sumber tegangan yang diubungkan secara seri dengan sebuah tahanan ekuivalennya
pada dua terminal yang diamati
Tujuan sebenarnya dari teorema ini adalah untuk menyederhanakan analisis rangkaian,
yaitu membuat rangkaian pengganti berupa sumber tegangan yang dihubungkan secara
seri dengan suatu resistansi ekuivalennya.
i
i
a
+
Rangkaian
Linier A
V
Rangkaian
B
Rangkaian
Linier A
+
- v
b
Cara memperoleh resistansi penggantinya (Rth) adalah dengan mematikan atau
menonaktifkan semua sumber bebas pada rangkaian linier A ( untuk sumber tegangan
tahanan dalamnya = 0 atau rangkaian short circuit dan untuk sumber arus tahanan
dalamnya = ∞ atau rangkaian open circuit).
Jika pada rangkaian sumber dependent atau sumber tak bebas, maka untuk
memperoleh resistansi penggantinya, maka terlebih dahulu harus dicari arus hubung
singkat (isc), sehingga nilai resistansi penggantinya ( Rth) didapatkan dari nilai tegangan
pada kedua terminal yang di open ciruit dibagi dengan arus pada kedua terminal yang di
short circuit.
Langkah – langkah penyelesaian dengan teorema Thevenin:
1. Cari dan tentukan titik terminal a – b dimana parameter ditanyakan
2. Lepaskan komponen pada titik a – b tersebut, jadikan open circuit terminal a – b,
kemudian hitung nilai tegangan di titik a – b tersebut ( vab = vth )
3. Jika semua arusnya adalah sumber bebas, maka tentukan nilai tahanan diukur
pada titik a – b tersebut saat semua sumber di non aktifkan dengan cara diganti
dengan tahanan dalamnya ( untuk sumber tegangan bebas diganti dengan short
circuit dan untuk sumber arus bebas diganti dengan rankaian open circuit ) (Rab =
Rth )
4. Jika terdapat sumber arus tak bebas, maka untuk mencari nilai tahanan
pengganti Theveninnya didapatkan dengan cara Rth =
5. Untuk mencari
, terminal titik a – b tersebut dihubungingkatkan dan dicari
arus yang mengalir pada titik tersebut (
= ),
6. Gambarkan kembali rangkaian pengganti Theveninnya, kemudian pasangkan
kembali komponen yang tadi dilepas da hitung parameter yang ditanyakan.
Kegunaan utama teorema Thevenin ini adalah memungkinkan suatu rangkaian untuk
digantikan oleh sepasang kutub keluaran, dan hasilnya dapat dipakai untuk menghitung
pengaruh suatu beban yang dipasangkan pada kutub – kutub keluaran itu, atau akibat yang
diperoleh beban karena sifat – sifat rangkaian tersebut.
Soal
Tentukan nilai arus I dengan teorema Thevenin
4Ω
i
12Ω
DC
3 A
6Ω
6 Ω
12 Ω
Tentukan titik a – b pada R dimana parameter i ditanyakan, kemudian hitung tegangan di
titik a – b pada saat terbuka.
4Ω
12 V
DC
a
3A
6Ω
b
12 Ω
4Ω
V1
12 V
DC
a
3 A
6Ω
V1 - 12
b
12 Ω
Tinjau node voltage v1 :
V1
6
+
v1
12
12
3 = 0 v1  v1  12  3  0
6
12
2v1  v1  12  36  0
3v1  48
2v1 + v1 -12 – 36 = 0
v  16v
3v1 = 48
48 = 16 V 1
3
vab  voc  12  v1  12  16  28v
Sehingga
=
= 12 +
= 12 + 16 = 28 V
Rth dicari ketika semua sumber bebasnya tidak aktif ( diganti dengan tahanan dalamnya ) dilihat
dari titik a – b :
4Ω
a
6Ω
b
12 Ω
Rth = 6 x 12 + 4 = 4 + 4 = 8Ω
6 + 12
R .R
RTh  1 2  R3
R1  R2
6 x12
RTh 
4
pengganti Thevenin:
6Rangkaian
 12
RTh  4  4
RTh  8
a
8 Ω
28 V
i
DC
6 Ω
b
Sehingga:
i = 28
= 28 = 2 A
8+6
I
v
RTh  R4
28
14
I  2A
I
14
Daftar Pustaka
 Budiono Mismail, Rangkaian listrik, 1981 Surabaya Lembaga penerbitan Universitas
Brawijaya Malang
 Harmonyati B.K, 1981, Rangkaian Listrik 1, Institut Teknologi Bandung, Bandung