BAB III - surya sebayang

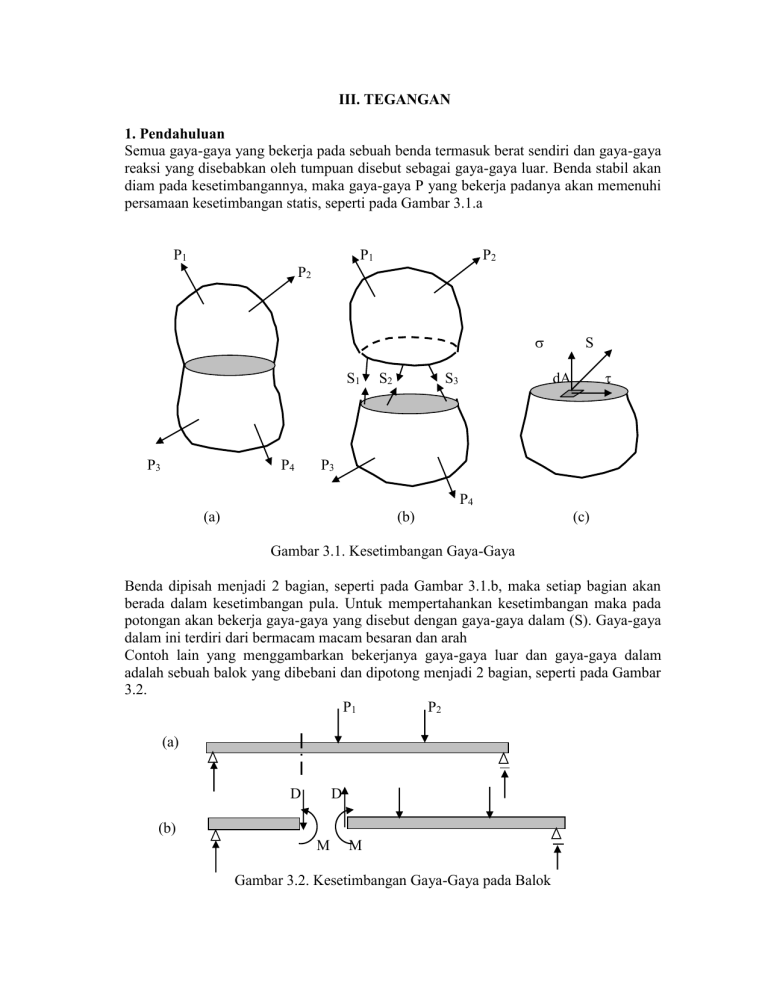
III. TEGANGAN
1. Pendahuluan
Semua gaya-gaya yang bekerja pada sebuah benda termasuk berat sendiri dan gaya-gaya
reaksi yang disebabkan oleh tumpuan disebut sebagai gaya-gaya luar. Benda stabil akan
diam pada kesetimbangannya, maka gaya-gaya P yang bekerja padanya akan memenuhi
persamaan kesetimbangan statis, seperti pada Gambar 3.1.a
P1
P1
P2
P2

S1
P3
P4
S2
S3
S

dA
P3
P4
(a)
(b)
(c)
Gambar 3.1. Kesetimbangan Gaya-Gaya
Benda dipisah menjadi 2 bagian, seperti pada Gambar 3.1.b, maka setiap bagian akan
berada dalam kesetimbangan pula. Untuk mempertahankan kesetimbangan maka pada
potongan akan bekerja gaya-gaya yang disebut dengan gaya-gaya dalam (S). Gaya-gaya
dalam ini terdiri dari bermacam macam besaran dan arah
Contoh lain yang menggambarkan bekerjanya gaya-gaya luar dan gaya-gaya dalam
adalah sebuah balok yang dibebani dan dipotong menjadi 2 bagian, seperti pada Gambar
3.2.
P1
P2
(a)
D
D
(b)
M
M
Gambar 3.2. Kesetimbangan Gaya-Gaya pada Balok
31
Balok setelah dipotong akan tetap berada dalam kesetimbangan apabila gaya-gaya dalam
momen M dan gaya lintang D bekerja pada penampang yang terpotong.
2. Tegangan Normal dan Tegangan Geser
Adanya gaya-gaya dalam pada penampang akan menyebabkan timbulnya tegangan pada
penampang tersebut. Tinjau gaya yang bekerja pada suatu irisan dA pada Gambar 3.1.c.
Tegangan Normal adalah tegangan yang tegak lurus terhadap suatu irisan yang secara
matematis dirumuskan sebagai berikut:
N
A
Namun untuk keperluan praktis rumus diatas dapat ditulis sebagai berikut:
  lim
A0

N
A
 : Tegangan normal
N : Gaya tegak lurus penampang, bekerja pada titik berat
penampang
A : Luas penampang.
Tegangan Geser adalah tegangan yang sejajar terhadap suatu irisan yang secara
matematis dirumuskan sebagai berikut:
D
A  0  A
Namun untuk keperluan praktis rumus diatas dapat ditulis sebagai berikut:
  lim

D
A
 : Tegangan geser rata-rata
D : Gaya sejajar penampang
A : Luas penampang.
Gambar 3.3 Pengujiaan Tegangan Normal dan Tegangan Geser
32
3. Satuan
Tegangan normal dan tegangan geser dihitung dalam satuan gaya dibagi dengan satuan
luas. Gaya adalah vektor sedangkan luas adalah skalar maka hasil baginya juga
merupakan vektor.
Satuan dasar SI adalah meter (m) untuk satuan panjang, kilogram (kg) untuk satuan
massa, dan detik (s) untuk satuan waktu. Satuan gaya didefinisikan sebagai satuan massa
dikalikan dengan satuan percepatan yaitu kilogram meter perdetik kwadrat (kg.m/s 2)
disingkat dengan newton (N). Satuan tegangan adalah newton per meter kwadrat (N/m2)
disingkat dengan pascal (Pa). Tegangan dalam satuan Pascal secara numeric sangat kecil
bila dibandingkan dengan satuan-satuan tegangan lain yang biasa dipakai. Oleh karena
itu satuan tegangan lebih dapat diterima apabila menggunakan satuan N/mm2 yang sama
dengan megapascal (106 Pa = MPa), satuan MPa ini telah mendapat pengakuan yang
luas untuk satuan tegangan.
4. Contoh-Contoh
Contoh 3.1.
Sebatang baja dengan diameter 19 mm mengalami gaya tarik sebesar 100 kN, hitunglah
tegangan yang terjadi pada batang baja.
Penyelesaian:

N
A
N = 100 kN = 100000 N
A = 0,25..192 = 283,5287 mm2
100000

 352,698 N/mm2 = 352,698 MPa
283,5287
Contoh 3.2.
Sebuah silinder beton dengan diameter 150 mm mengalami gaya tekan sebesar 600 kN,
hitunglah tegangan yang terjadi pada silinder beton.
Penyelesaian:

N
A
N = 600 kN = 600000 N
A = 0,25..1502 = 17671,4587 mm2
600000

 33,953 N/mm2 = 33,953 MPa
17671,4587
33
Contoh 3.3
Sebuah pondasi seperti tergambar memikul beban 20 kN/m2. Hitunglah tegangan yang
terjadi pada dasar pondasi. Berat isi pondasi sebesar 24 kN/m3
0,5 m
1m
1m
0,5 m
Penyelesaian:
tampak samping
Tegangan yang terjadi pada dasar pondasi diakibatkan oleh gaya normal. Gaya normal
yang bekerja terdiri dari 2 macam:
1. Gaya normal akibat beban 20 kN/m2
2. Gaya normal akibat berat sendiri pondasi.
1. Gaya normal akibat beban
N1 = luas bidang yang dibebani x besar beban
N1 = 0,5m.0,5m.20 kN/m2 = 5 kN
2. Gaya normal akibat berat sendiri pondasi
N2 = volume pondasi x berat volume pondasi
N2 = [ 1 2 (1 +0,5). 1.0,5] 24 = 9 kN
N = N1 + N2 = 5 + 9 = 14 kN
A = luas alas pondasi = 1.0,5 = 0,5 m2 = 0,5.106 mm2

N
14.10 3
=
 0,028 MPa
A 0,5.10 6
Contoh 3.4.
Dua buah pelat baja disambung dengan menggunakan baut berdiameter 20 mm, seperti
pada gambar dibawah.
1. Hitung tegangan normal rata-rata dari pelat dimana tidak terdapat lobang
2. Hitung tegangan normal rata-rata pelat pada penampang kritis
3. Hitung tegangan geser rata-rata pada baut
4. Hitung tegangan dukungan antara baut dan pelat
34
45 kN
45 kN
150 mm
10 mm
10 mm
potongan memanjang
Penyelesaian
1. Tegangan normal rata-rata dari pelat dimana tidak terdapat lubang:
N 45.10 3
=
 30 MPa
A 150.10
2. Penampang kritis merupakan penampang yang telah dikurangi dengan lubang
baut sehingga :

A = 150.10 – 2.20.10
A = 1100 mm2
20 mm

150 mm
3
N 45.10
=
 40,9 MPa
A
1100
20 mm
10 mm
3. Tegangan geser rata- rata pada baut:
Dalam hal ini ada dua penampang baut yang tergeser, sehingg luas penampang geser
baut :
A = 2. 1 4 . .20 2

D
45.10 3

 71,65 MPa
A 2. 14 . .20 2
4. Tegangan dukungan antara baut dengan pelat
Akibat gaya yang bekerja maka pelat yang berlubang akan didesak/ditekan oleh
baut, luas penampang yang terdesak (lihat gambar pada penyelesaian bagian 2)
A = 2.20.10 = 400 mm2

D 45.10 3

 112,5 MPa
A
400