Modul 11- MOMEN PUSAT BERAT

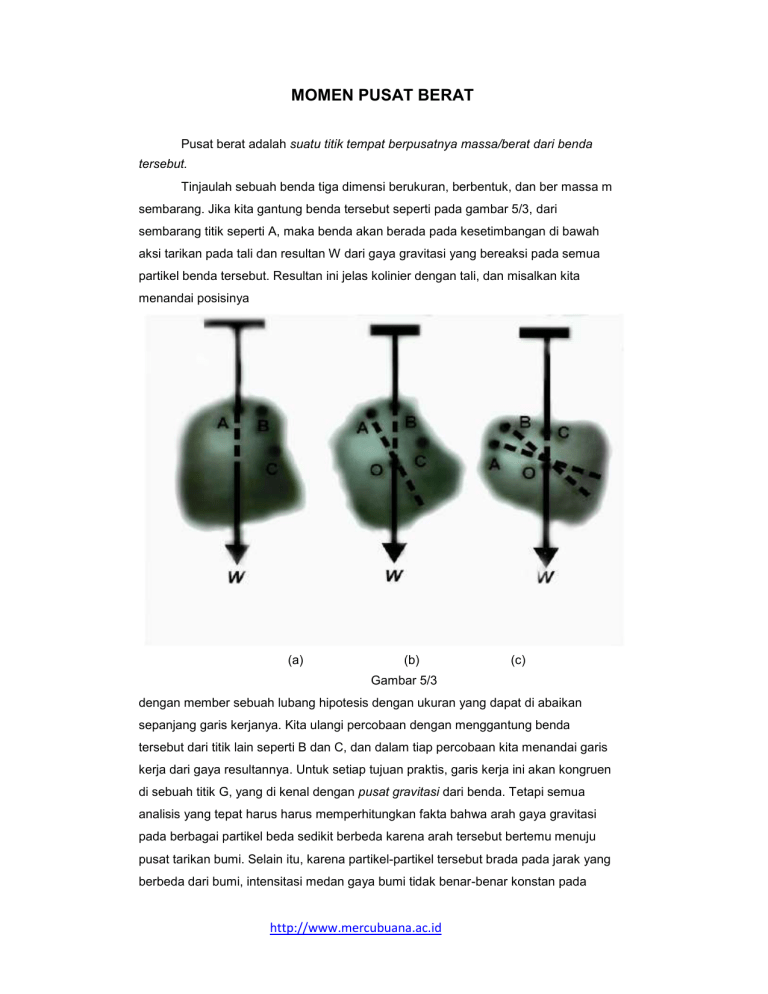
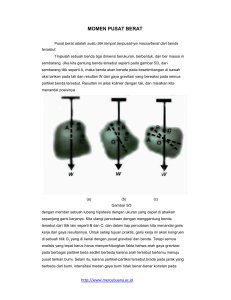
MOMEN PUSAT BERAT
Pusat berat adalah suatu titik tempat berpusatnya massa/berat dari benda
tersebut.
Tinjaulah sebuah benda tiga dimensi berukuran, berbentuk, dan ber massa m
sembarang. Jika kita gantung benda tersebut seperti pada gambar 5/3, dari
sembarang titik seperti A, maka benda akan berada pada kesetimbangan di bawah
aksi tarikan pada tali dan resultan W dari gaya gravitasi yang bereaksi pada semua
partikel benda tersebut. Resultan ini jelas kolinier dengan tali, dan misalkan kita
menandai posisinya
(a)
(b)
(c)
Gambar 5/3
dengan member sebuah lubang hipotesis dengan ukuran yang dapat di abaikan
sepanjang garis kerjanya. Kita ulangi percobaan dengan menggantung benda
tersebut dari titik lain seperti B dan C, dan dalam tiap percobaan kita menandai garis
kerja dari gaya resultannya. Untuk setiap tujuan praktis, garis kerja ini akan kongruen
di sebuah titik G, yang di kenal dengan pusat gravitasi dari benda. Tetapi semua
analisis yang tepat harus harus memperhitungkan fakta bahwa arah gaya gravitasi
pada berbagai partikel beda sedikit berbeda karena arah tersebut bertemu menuju
pusat tarikan bumi. Selain itu, karena partikel-partikel tersebut brada pada jarak yang
berbeda dari bumi, intensitasi medan gaya bumi tidak benar-benar konstan pada
http://www.mercubuana.ac.id
harus sama dengan Wx ,yaitu momen dari jumlah. Oleh karena itu, xW = x d W .
Dengan pernyataan yang serupa untuk kedua komponen lainnya, kita dapat
menyatakan
 x dW
X=
W
koordinat
,y=
 y dW
W
pusat
gravitasi
G
sebagai
 z dW
, z=
W
(5/1a)
Untuk membayangkan momen fisis akibat gaya gravitasi guna memperoleh
persamaan ketiga, kita dapat mengubah posisi benda tersebut dan sumbu yang
tergantung sedemikian rupa sehingga sumbu z menjadi horisontal. Perlu di ketahui
bahwa pembilang dari masing masing persamaan ini menyatakan jumlah momen,
sedangkan perkalian W dan koordinat yang berkaitan dari G menyatakan momen
dari jumlah. Prinsip momen ini berulang kali di pakai dalam seluruh mekanika.
http://www.mercubuana.ac.id
Dalam kebanyakan persoalan, perhitungan posisi pusat massa dapat di
sederhanakan dengan pemilihan sumbu acuan yang tepat. Secara umum sumbu ini
harus di tempatkan sedemikian rupa sehingga dapat menyederhanakan persamaan
batas sebanyak mungkin. Jadi koordinat polar akan bermanfaat untuk benda yang
memiliki batas melingkar. Petunjuk penting lain dapat di ambil dari peninjauan
simetri. Apabila terdapat sebuah garis atau budang simetri pada sebuah benda
homogen, maka sumbu atau bidang koordinat harus di pilih agar berimpit dengan
garis atau bidang ini. Pusat massa selalu terletak pada garis atau bidang demikian,
karena momen akibat elemen-elemen yang terlokasi secara simetris selalu akan
saling menghilangkan, dan benda tersebut dapat di tinjau sebagai benda yang
tersusun dari pasangan elemen ini.
Koordinat titik berat suatu sistem benda dengan berat masing-masing W 1, W 2,
........., W i ; yang terletak pada koordinat (x1,y1), (x2,y2), ............, (xi,yi) adalah:
X=(
Y=(
Wi . Xi)/(Wi)
Wi . Yi)/(Wi)
LETAK/POSISI TITIK BERAT
1. Terletak pada perpotongan diagonal ruang untuk benda homogen berbentuk
teratur.
2. Terletak pada perpotongan kedua garis vertikal untuk benda sembarang.
3. Bisa terletak di dalam atau diluar bendanya tergantung pada homogenitas
dan bentuknya.
TITIK BERAT BEBERAPA BENDA
Nama
Letak Titik Berat
Keterangan
Garis lurus
yo = 1/2 AB
z = di tengah-tengah AB
Busur lingkaran
yo = AB/AB . R
AB = tali busur
AB = busur AB
R = jari-jari lingkaran
Busur setengah lingkaran
yo = 2.R/p
R = jari-jari lingkaran
Juring lingkaran
yo = AB/AB.2/3.R
AB = tali busur
AB = busur AB
R = jari-jari lingkaran
Setengah lingkaran
yo = 4.R/3
http://www.mercubuana.ac.id
R = jari-jari lingkaran