9. Teori Dasar Digital - Otomasi Sistem Produksi

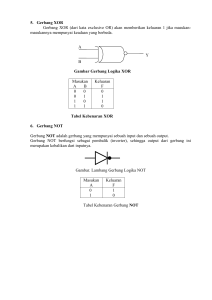
TEORI DASAR
DIGITAL
Leterature :
(1) Frank D. Petruzella, Essentals of Electronics, Singapore,McGrraw-Hill Book Co, 1993, Chapter 41
(2) Ralph J. Smith, Circuit, Devices, and System, Fourth Edition, California, John Wiley & Sons, Inc.,
1992, Chapter 13 - 14
OTOMASI SISTEM PRODUKSI
1
ELEKTRONIKA DIGITAL
• Elektronika digital telah menyebabkan terjadinya perubahan besar dalam industri, baik dalam industri elektronika maupun industri-industri yang lain.
• Beberapa tahun silam, aplikasi elektronika digital
terbatas hanya pada sistem komputer.
• Belakangan ini penggunaan elektronika digital semakin meluas, seperti misalnya mesin robot dikontrol
menggunakan rangkaian digital, pengendalian dan
pemonitoran fungsi mesin otomobil, peralatan musik,
kontrol panel (keyboard), dan banyak lagi penggunaan
yang lainnya.
OTOMASI SISTEM PRODUKSI
2
Bentuk gelombang signal digital
•
Rangkaian digital beroperasi hanya menggunakan signal dua
keadaan (two-state signal), yang pada umumnya dinyatakan
dengan dua level tegangan berbeda yaitu tinggi dan rendah (high
and low) masing-masing dengan simbol H dan L  gambar (a).
(a)
(b)
•
•
Cara lain yang juga digunakan untuk menyatakan dua keadaan
tersebut adalah 0 dan 1 masing-masing sebagai pengganti level
L dan level H  gambar (a).
Semua tegangan yang berada di atas level standar menyatakan
signal ON (1), dan tegangan di bawah level standar menyatakan
signal OFF (0)  gambar (b).
OTOMASI SISTEM PRODUKSI
3
SISTEM BILANGAN BINER
•
•
Dalam elektronika digital, bilangan biner digunakan sebagai
kode untuk menyatakan bilangan desimal, huruf alfabet, dan
beberapa jenis informasi yang lain.
Sistem bilangan biner merupakan cara lain yang sederhana
untuk menyatakan bilangan, dimana hanya digunakan dua digit
yaitu 0 dan 1.
Count
Decimal number
Binary number
Zerq
0
0
One
1
1
Two
2
10
Three
3
11
Four
4
100
Five
5
101
Six
6
110
Seven
7
111
Eight
8
1000
Nine
9
1001
Ten
10
1010
Eleven
11
1011
Twelve
12
1100
Thirteen
13
1101
Fourteen
14
1110
Fifteen
15
1111
•
•
Sistem biner dapat digunakan dengan rangkaian
digital karena prosesnya
hanya terdiri dari signal
digital level high dan low
saja.
Setiap posisi bilangan biner hanya dapat berupa
angka 0 atau 1, dan posisi berikutnya kemudian
ditempatkan di sebelah
kiri. Dalam tabel ditunjukkan
bilangan
biner
untuk nilai desimal 1
sampai dengan 15.
OTOMASI SISTEM PRODUKSI
4
Pembobotan dalam sistem desimal
•
•
•
Bobot dari bilangan desimal tergantung dari jumlah digit yang
membentuknya dan bobot posisi yang ditempati oleh setiap digit
bilangan tersebut.
Dalam sistem bilangan desimal, bobot posisi pertama, dimulai
dari posisi yang paling kanan adalah 0; kedua 1; ketiga 2; dan
seterusnya hingga posisi yang terakhir.
Setiap posisi berturut-turut dikalikan dengan 100, 101, 102, 103
(atau 1, 10, 100, 1000) dan seterusnya, dan jumlah hasil
perkalian merupakan bobot dari keseluruhan bilangan tersebut.
Decimal number
3
2
1
0
1
9
6
2
10
2 x 100 = 2 x
1=
2
6 x 101 = 6 x
10 =
60
9 x 102 = 9 x
100 =
900
1 x 103 = 1 x 1000 = 1000
1962
(Sum of products)
OTOMASI SISTEM PRODUKSI
5
Konversi sistem biner ke sistem desimal
•
•
Konversi bilangan biner ke bilangan desimal dapat dilakukan
dengan cara yang hampir sama.
Setiap posisi berturut-turut dikalikan dengan 20, 21, 22, 23 , 24, 25,
26, 27 (atau 1, 4, 8, 16, 32, 64, 128) dan seterusnya, dan jumlah
hasil perkalian merupakan bobot dari keseluruhan bilangan
desimal hasil konversi dari bilangan biner tersebut.
Binary number
7
6
5
4
3
2
1
0
1
0
1
0
1
1
0
1
2
1 x 20 = 1 x
1 =
1
0 x 21 = 0 x
2 =
0
1 x 22 = 1 x
4 =
4
1 x 23 = 1 x
8 =
8
0 x 24 = 0 x
16 =
0
1 x 25 = 1 x
32 =
32
0 x 26 = 0 x
64 =
0
1 x 27 = 1 x 128 = 128
Decimal number
173
(Sum of products)
OTOMASI SISTEM PRODUKSI
6
Bit, nibble, byte, dan word
•
•
•
Satu angka biner tunggal disebut bit; dalam sistem digital,
seluruh informasi disajikan dengan sederetan bit-bit.
Satu deretan dengan 4-bit disebut satu nibble; satu deretan 8-bit
disebut byte.
Satu byte dapat mempresentasikan angka desimal dari 0 sampai
dengan 255 (disusun dalam 28 = 256 kombinasi yang berbeda).
MSB
0
Bit
1
1
0
0
1
1
0
0
0
1
Byte
LSB
1
1
0
1
1
Byte
16 - bit word
•
•
•
Kelompok bit-bit dalam deretan yang berurutan disebut word .
Pada umumnya komputer menggunakan 8 atau 16 bit untuk
membentuk sebuah word ; gambar di atas word dibangun dari 2
byte.
Least significant bit (LSB) adalah digit yang menunjukkan nilai
terendah dan most significant bit (MSB) adalah digit yang
menunjukkan nilai terbesar.
OTOMASI SISTEM PRODUKSI
7
Data biner
•
•
Saklar dapat digunakan untuk memasukkan data biner ke dalam
peralatan digital  Gambar berikut ini menunjukkan bilangan
biner 11000101, atau dalam bilangan desimal 197.
Indikator sinar seperti LED kadang-kadang digunakan untuk
membaca atau mendisplaikan data biner dalam peralatan
digital.
OTOMASI SISTEM PRODUKSI
8
Sistem bilangan heksadesimal
•
•
•
•
Sistem biner memerlukan lebih banyak digit daripada sistem
desimal, sehingga susah untuk dibaca dan ditulis.
Untuk mengatasi masalah ini, sistem bilangan yang lain
digunakan agar lebih mudah dan lebih efisien dikomunikasikan
dengan rangkaian digital.
Sistem bilangan tersebut merupakan kelipatan dua dan
termasuk oktal, heksadesimal, desimal kode biner (binary code
decimal, BCD).
Gambar berikut ini menunjukkan perbandingan antara sistem
bilangan heksadesimal, biner, desimal.
Hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Binary
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
Decimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
•
•
Heksadesimal terdiri dari
angka 0 sampai dengan 9
ditambah lagi dengan huruf A sampai dengan F.
Sistem bilangan ini dapat
digunakan untuk menghitung dari 0 hingga 15 dengan satu digit karakter
tunggal.
OTOMASI SISTEM PRODUKSI
9
Cara menuliskan bilangan heksadesimal
•
•
8-bit bilangan biner dapat dituliskan dalam heksadesimal
dengan membagi menjadi dua kelompok, dimana masing-masing
kelompok terdiri dari 4-bit bilangan biner.
Masing-masing kelompok 4-bit menunjukkan bilangan 0 hingga
15 (0000 dan 1111).
Contoh
• Bilangan desimal 47 dalam sistem biner adalah 0010 1111, dan
dalam heksadesimal adalah 2F, dimana 2 = 0010 dan F = 1111
(lihat tabel).
Decimal
number
4
0
0
Equivalent
hexadecimal
number
1
7
0
1
2
F
1
1
OTOMASI SISTEM PRODUKSI
1
Equivalent
binary
number
10
GERBANG LOGIKA
•
•
Gerbang logika dapat didefinisikan sebagai peralatan yang
dapat menghasilkan suatu output hanya bila telah ditentukan
sebelumnya kondisi input yang ada.
Dalam hal ini digunakan istilah gerbang karena menunjukkan
keadaan terbuka atau tertutup.
Gerbang AND
•
•
Rangkaian saklar sederhana dalam
gambar di samping kiri menunjukkan
bahwa bateri hanya dapat mensuplai
lampu bila saklar A dan B dalam
keadaan ON (1).
Gambar (A) dan (B) di bawah berturut-turut menunjukkan simbol dan
tabel kebenaran (truth table) gerbang AND.
A. Standard AND-gate symbol
B. AND truth table
OTOMASI SISTEM PRODUKSI
11
•
Gambar (C) menunjukkan skematik rangkaian AND dan gambar
(D) menunjukkan chip IC gerbang AND dua-input.
C. Circuit schematic
•
D. Typical quad two-input AND gate IC chip
Gerbang AND dapat memiliki lebih dari dua input.
OTOMASI SISTEM PRODUKSI
12
Diagram waktu gerbang AND
•
Bila input A dan input B merupakan
pulsa, maka bentuk pulsa outputnya
sesuai dengan kaidah tabel kebenarannya (truth table).
Gerbang OR
•
•
Rangkaian saklar sederhana berikut ini menunjukkan bahwa
bateri dapat mensuplai lampu bila saklar A dan/atau saklar B
dalam keadaan ON (1).
Gambar (A) dan (B) di bawah berturut-turut menunjukkan
simbol dan tabel kebenaran gerbang OR.
A. Standard OR-gate
symbol
B. OR truth table
OTOMASI SISTEM PRODUKSI
13
•
Gambar (C) menunjukkan skematik rangkaian OR dan gambar (D)
menunjukkan chip IC gerbang OR dua-input.
C. Circuit schematic
•
D. Typical quad two-input OR gate IC chip
Gambar (E) menunjukkan aplikasi gerbang dalam otomotif dan
gambar (F) menunjukkan diagram waktu bila input A dan B
berupa pulsa.
E. Typical automotive application
OTOMASI SISTEM PRODUKSI
F. Timing diagram
14
Gerbang NOT
•
•
•
Tidak seperti gerbang AND dan OR, gerbang NOT hanya memiliki satu input.
Rangkaian saklar sederhana berikut ini menunjukkan bahwa
bateri dapat mensuplai lampu ( A = 1) bila saklar A dalam keadaan OFF (0), sedang bila saklar A dalam keadaan ON (1) arus
listrik yang melewati lampu sangat kecil sehingga tidak dapat
menyalakan lampu ( A = 0).
Gambar (A) dan (B) di bawah berturut-turut menunjukkan
simbol dan tabel kebenaran gerbang NOT (INVERTER).
A. Standard INVERTER symbol
B. INVERTER truth table
OTOMASI SISTEM PRODUKSI
15
•
Gambar (C) menunjukkan skematik rangkaian NOT dan gambar
(D) menunjukkan chip IC gerbang NOT input tunggal.
C. Circuit schematic
•
D. Typical INVERTER IC chip
Gambar (E) menunjukkan bahwa dalam operasi gerbang NOT,
kondisi pulsa high (1) pada input dibalik menjadi kondisi low (0)
pada output dan sebaliknya kondisi pulsa low (0) pada input
dibalik menjadi kondisi high (1) pada output.
E. Pulsed operation
OTOMASI SISTEM PRODUKSI
16
Gerbang NAND (NOT-AND)
•
Gerbang NAND merupakan kombinasi gerbang AND dan INVERTER, gambar (A) menunjukkan simbol standar gerbang NAND
sedang gambar (B) merupakan gerbang NAND equivalen yang
dirangkai dari gerbang AND dan INVERTER.
A. Standard NAND-gate symbol
B. Equivalent NAND-gate wired
using an AND-gate and INVERTER
•
•
C. NAND truth table
D. Typical quad two-input NAND
gate IC chip
Tabel kebenaran gerbang NAND dalam gambar (C) menujukkan
nilai output yang berlawanan dengan nilai output tabel
kebenaran gerbang AND.
Gambar (D) menunjukkan chip IC gerbang NAND dua-input.
OTOMASI SISTEM PRODUKSI
17
•
Gambar (E) menunjukkan skematik rangkaian NAND dan gambar
(F) menunjukkan diagram waktu bila input A dan B berupa pulsa.
E. Circuit schematic
F. Timing diagram
Gerbang NOR (NOT-OR)
•
Gerbang NOR merupakan kombinasi gerbang OR dan INVERTER,
gambar (A) menunjukkan simbol standar gerbang NOR sedang
gambar (B) merupakan gerbang NOR equivalen yang dirangkai
dari gerbang OR dan INVERTER.
B. Equivalent NOR-gate wired using
an OR-gate and INVERTER
OTOMASI SISTEM PRODUKSI
18
A. Standard NOR-gate symbol
•
•
Tabel kebenaran gerbang NOR dalam gambar (C) menujukkan
nilai output yang berlawanan dengan nilai output tabel
kebenaran gerbang OR.
Gambar (D) menunjukkan chip IC gerbang NOR dua-input.
C. NOR truth table
•
D. Typical quad two-input NOR gate IC chip
Gambar (E) menunjukkan skematik rangkaian NOR dan gambar
(F) menunjukkan diagram waktu bila input A dan B berupa pulsa.
E. Circuit schematic
F. Timing diagram
OTOMASI SISTEM PRODUKSI
19
Fungsi Eksklusif-OR (Exclusive-OR , XOR )
•
•
•
•
Kombinasi gerbang yang sering digunakan adalah fungsi ekslusif-OR (XOR) seperti ditunjukkan dalam gambar di bawah ini.
Gerbang XOR juga ada dalam bentuk IC dengan simbol tersendiri, jadi tidak perlu menghubungkan gerbang-gerbang terpisah
untuk membangun fungsi XOR tersebut.
Dari tabel kebenarannya dapat dilihat bahwa output hanya akan
1 bila salah satu inputnya 1, tetapi bila kedua-duanya memiliki
digit yang sama maka outputnya 0.
Gerbang XOR sering digunakan untuk membandingkan dua
bilangan biner seperti gambar berikut ini.
OTOMASI SISTEM PRODUKSI
20
•
Sebagai contoh bilangan biner yang menunjukkan temperatur
dapat dibandingkan dengan bilangan biner yang menunjukkan
level tegangan dari sensor pendingin (coolant sensor) untuk
menentukan temperatur pendingin.
•
Bilangan yang menunjukkan temperatur dihubungkan ke satu
input gerbang XOR, dan bilangan yang menunjukkan temperatur
pendingin dihubungkan ke input yang lain.
Bila kedua input 1 atau keduanya 0, maka outputnya 0, jadi bila
kodenya sama berarti temperatur yang diinginkan telah sesuai.
•
OTOMASI SISTEM PRODUKSI
21
Aljabar Boolean
•
•
•
Kombinasi rangkaian logika dapat direncanakan menggunakan
aljabar Boolean.
Fungsi rangkaian dinyatakan dengan persamaan Boolean.
Gambar di atas menunjukkan bagaimana fungsi AND, NAND, OR,
NOR, dan NOT digunakan untuk membentuk persamaan Boolean.
OTOMASI SISTEM PRODUKSI
22
Teorema Boolean
•
Hukum-hukum dasar diperlihatkan dalam tabel berikut ini
Hukum-hukum Boolean dengan
0 dan 1
OR
0
0
1
1
+
+
+
+
0
1
0
1
=
=
=
=
AND
0
1
1
1
0
0
1
1
.
.
.
.
0
1
0
1
=
=
=
=
0
0
0
1
Teorema-teorema Boolean
dengan satu variabel
NOT
OR
AND
0 =1
1 =0
A+0=A
A+1=1
A+A=A
A+A=1
A.0=0
A.1=A
A.A=A
A.A=0
NOT
A =A
Teorema-teorema Boolean untuk lebih dari satu variabel
Hukum Komutasi
Hukum Asosiasi
Teorema DeMorgan
A+B=B+A
A + (B + C) = (A + B) + A
A+B=A.B
A.B=B.A
A . (B . C) = (A . B) . A
A.B=A+B
Hukum Serapan
Hukum Distribusi
A + (A . B) = A
A . (B + C) = (A . B) + (A . C)
A . (A + B) = A
A + (B . C) = (A + B) . (A + C)
OTOMASI SISTEM PRODUKSI
23
Gerbang XOR dalam persamaan Boolean
•
Persamaan Boolean untuk gerbang XOR adalah sebagi berikut :
A XOR B = A
A
A
B
B
B = (A + B) . AB
A
A+B
B
Simbol gerbang XOR
A
Tabel kebenaran
A B
0
0
1
1
0
1
0
1
A
AB
B
0
1
1
0
Rangkaian XOR
OTOMASI SISTEM PRODUKSI
24
B
Contoh soal 1
Tunjukkan teorema-teorema berikut ini dengan tabel kebenaran.
A+A=1
dan
A.1 =A
Jawab :
Berdasarkan teorema Boolean, tabel kebenarannya adalah :
A A
0
1
1
0
A+A
1
1
A
0
A.1
0
1
1
Contoh soal 2
Tunjukkan A + (A . B) = A dengan teorema dasar lainnya.
Jawab :
Penguraian dengan teorema distribusi :
A + (A . B) = (A + A) . (A + B) = A . (A + B) = A.A + A.B
Substitusi A. 1 untuk A.A :
A + (A . B) = A.A + A.B = A.1 + A.B = A . (1 + B) = A
OTOMASI SISTEM PRODUKSI
25
Contoh soal 3
Gunakan gerbang NAND untuk membentuk gerbang OR dua-input.
Jawab :
Fungsi satu gerbang OR dua-input adalah Y = A + B
Berdasarkan teorema DeMorgan : A + B = A . B  Y = A + B = A . B
Ini berarti output Y dapat dibentuk dengan satu gerbang NAND
dengan dua input NOT.
Karena A . A = A, ini berarti bila kedua input gerbang NAND disatukan akan melakukan operasi NOT.
Jadi rangkaian ekuivalen gabungan gerbang NAND dapat digambarkan sebagai berikut :
A
A
Y=A+B
B
B
OTOMASI SISTEM PRODUKSI
26
Contoh soal 4
Tunjukkan bahwa rangkaian di bawah ini dapat diganti dengan satu
gerbang NAND tunggal dengan cara (a) membuat tabel kebenaran,
(b) dengan aljabar Boolean.
A
AB
B
Y
Output
A
A +B
Jawab :
(a) Tabel kebenaran :
Jadi Y = A B

A B
0
0
1
1
0
1
0
1
AB
A+B
Y
1
1
1
0
0
0
1
0
1
1
1
0
gerbang NAND
OTOMASI SISTEM PRODUKSI
27
(b) Aljabar Boolean :
Output rangkaian logika dapat dituliskan sebagai berikut :
Y=AB + A+B
= (A + B) + A B
(Teorema DeMorgan)
= A + ( B + A B)
(Hukum asosiasi)
= A + B (1 + A)
(Hukum distribusi)
=A+B
(1 + A = 1)
=AB
(Teorema DeMorgan)
Jadi Y = A B

A
B
gerbang NAND
Y = A.B
OTOMASI SISTEM PRODUKSI
28
Contoh soal 5
Tunjukkan bahwa rangkaian di bawah ini dapat diganti dengan satu
gerbang XOR tunggal dengan cara (a) membuat tabel kebenaran,
(b) dengan aljabar Boolean.
A
B
A
AB
B
Y
A
B
AB
Jawab :
(a) Tabel kebenaran :
OTOMASI SISTEM PRODUKSI
29