Sebuah batang yang panjangnya tak hingga diberi

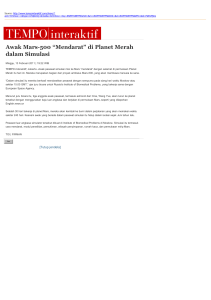
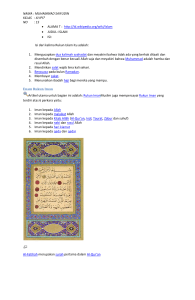
1. Perhatikan gambar 1! Sebuah batang yang panjangnya tak hingga diberi muatan
sehingga rapat muatan liniernya ( yaitu muatan per satuan panjang, dalam satuan
C/m) bernilai konstan γ. Hitunglah medan lisrik E di titik P yang berjarak y dari
batang tersebut! (Nilai maksimum 20)
(Petunjuk: Medan listrik yang bekerja pada titik P merupakan jumlah dari seluruh
medan listrik dari setiap muatan pada batang. Gunakan metode integral dengan
batas x dari - ∞ sampai ∞ )
dE
•P
θ
r
y
x
-
+ ++ + + ++ + + + + + + + + ++ + + + + + +
dx
0
Gambar 1. batang dengan muatan terdistribusi merata
2. Bidang berbentuk segitiga dengan kemiringan sudut sebesar θ dan bermassa M
bersama-sama dengan benda bermassa m1 dan m2 dihubungkan dengan katrol
sehingga membentuk sistem seperti pada gambar 2. Katrol dan tali yang digunakan
bermassa sangat kecil. Jika antara lantai dan bidang segitiga memiliki koefisien
gesekan statis μ, dan massa m2 bersentuhan tanpa gesekan dengan bidang, tentukan:
a. percepatan massa m1 dan m2, dan besarnya tegangan tali
b. koefisien gesekan terkecil sehingga bidang segitiga tetap dalam keadaan diam.
(Nilai maksimum 20)
m1
m2
M
θ
Gambar 2. bidang segitiga dengan dua benda terhubung tali
3. Sebuah loop berbentuk persegi yang panjang sisinya S berada di sebelah atas sebuah
kawat lurus dengan jarak a yang panjangnya tak hingga membawa arus I, seperti
ditunjukan pada gambar 3.
S
Physics is wonderful and
immensely beautiful
S
a
I
Gambar 3. loop persegi diletakan dekat kawat berarus
a. tentukan fluks B yang melalui loop
b. jika loop ditarik ke atas menjauhi kawat dengan kecepatan v, cari potensial
(GGL) yang dihasilkan!
c. apa yang terjadi jika loopditarik ke kiri dan ke kanan
d. berapakah muatan total yang melalui loop jika kawat berarus itu dipotong?
(Nilai maksimum 25)
dΦ
(Petunjuk: gunakan rumus Φ = ∫ B dA , ε = −
; dimana A adalah luas dari
dt
persegi, B adalah medan magnet, Ф adalah fluks magnet dan ε adalah potensial
1
GGL. Diketahui: ∫ dx = ln( x) )
x
4. Suatu sistem tediri dari cincin yang didalamnya terdapat benda P. Cincin tersebut
menggalinding tanpa slip di atas bidang datar. Kecepatan pusat massa cincin sebesar
vo saat benda P berada pada titik terendah A. B adalah titik tertinggi. Berapa nilai vo
agar cincin tidak melompat – lompat jika massa cincin sama dengan massa benda
P ? (Nilai maksimum 35)
B
A
Gambar 4. cincin yang menggelinding
5. Ana dan Ani adalah saudara kembar yang tinggal di Bumi yang sudah tidak aman
lagi, peperangan terus terjadi di Bumi yang mengakibatkan Ana dan Ani
berkeinginan untuk melakukan perjalanan keluar angkasa. Si Ana berkeinginan
untuk pergi ke sistem Tata Surya yang lain, Sedangkan adiknya Ani ingin pergi ke
planet Mars untuk menetap disana karena lebih aman dibandingkan tinggal di
Bumi. Bantulah mereka untuk mewujudkan impiannya dengan konsep dasar fisika
yang Anda ketahui.
Lets get succes with
physics !
A
•
•X
Gambar 5. pesawat berada pada orbit planet Mars
a. Tentukanlah kelajuan minimum pesawat Ana dan Ani agar dapat lepas dari
pengaruh gaya gravitasi bumi sesuai dengan konsep dasar fisika. Massa bumi
Mb dan jari-jarinya Rb
b. Jika Ana dan Ani melakukan perjalanan dengan memanfaatkan system roket.
Tentukanlah besarnya gaya dorongan roket hingga menghasilkan kecepatan
sebesar kecepatan lepasnya!
c. Ketika telah sampai pada orbit Mars, Saudara kembar tersebut akhirnya
berpisah. Ana ingin melanjutkan perjalanannya keluar dari tata surya kita.
Sedangkan adiknya, Ani, ingin menuju permukaan planet Mars. Jika pesawat
yang dipakai oleh Ani bermassa ma dan mengorbit Planet Mars dalam lintasan
melingkar pada ketinggian hx. Untuk dapat mencapai permukaan planet Mars
,mesin jet pesawat ini dinyalakan di titik X dalam waktu yang singkat. Jika
kecepatan buang dari penyembur adalah u relative terhadap pesawat tersebut.
Jari-jari planet Mars adalah Rm dan percepatan gravitasinya gm. Ani yang cerdas
mengetahui bahwa untuk mencapai permukaan planet Mars di titik A hanya
tejadi jika pesawat berada pada sisi yang berlawanan sesuai gambar dengan
gambar 4. Hitunglah bahan bakar yang di perlukan dalam proses tersebut!
d
Ketika telah sampai di planet Mars Ani yang cerdas mencoba berbagai
pengetahuannya, Ani melemparkan sebuah logam menggunakan suatu alat
dengan kecepatan awal V0, Saat dibumi, dengan kecepatan awal yang sama
logam tersebut dapat mencapai ketinggian maksimum 25 meter. Berapakah
ketinggian maksimum yang dapat dicapai oleh logam tersebut ketika dilempar
dari permukaan mars,dengan asumsi massa planet mars sepersepuluh massa
planet Bumi dan jari-jarinya setengah dari jari-jari bumi! Dari asumsi tersebut
tentukan pula periode Revolusi planet Mars dan bandingkan dengan Bumi!
e. Di lain sisi, Ana yang melanjutkan perjalanan menuju Tata Surya yang lain,
pesawatnya harus lepas dari gravitasi tatasurya kita. Ketika itu ia masih berada
di orbit planet mars. Dengan bantuan gravitasi planet ini, kecepatan (besar dan
arah) pesawatnya akan berubah sedemikian sehingga kecepatan setelah berubah
ini mampu melepaskannya dari gravitasi tata surya kita. Hitung kecepatan
pesawat agar pesawat Ana tersebut bisa keluar dari system tata surya kita setelah
memotong orbit planet Mars! Di sini pesawat akan bertemu dengan planet Mars
dan Gravitasi planet Mars akan mengubah kecepatan pesawat sehingga
kecepatannya cukup untuk lepas dari pengaruh gravitasi tata surya kita.
(Nilai maksimum 50)
Catatan : untuk soal a dan b cukup dengan symbol variabelnya saja.
Data yang dimiliki si kembar :
Massa Bumi 5,98x1024 kg
Jari-jari bumi 6.4x106 m dan percepatan gravitasi di bumi sebesar 9,8 m/s2
Kecepatan bumi mengelilingi matahari 30 km/s dan perbandingan jarak bumi dan
mars dari matahari adalah 2/3