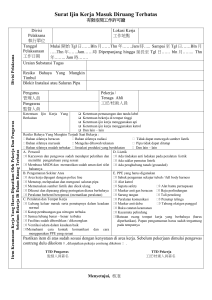
Integer Programmming (pemrograman bilangan bulat)

Integer Programmming
(pemrograman bilangan bulat)
• Masalah pemrograman bilangan bulat
murni
– IP dengan semua variabelnya bil bulat
• Masalah pemrograman bilangan bulat
campuran
– IP dengan beberapa variabelnya bulat
• Masalah pemrograman 0-1 (biner)
– IP dengan variabel bulat, hanya 0 dan 1
Contoh-contoh model dengan
Variabel “Bilangan Bulat”
Beberapa Model :
• Capital Budget ( anggaran dr modal )
• Multiperiod Capital Budgeting ( menganggar-kan modal dalam periode yang
berbeda)
• Knapsack Problem ( masalah Knapsack)
• Set Covering ( penutup himpunan )
Capital Budgeting
• Punya uang utk investasi Rp 14.000.000.
• Ada 4 jenis kesempatan investasi :
– Investasi 1 : butuh Rp 5.000.000 , akan berkembang mjd Rp
8.000.000
– Investasi 2 : butuh Rp 7.000.000 , akan berkembang mjd Rp
11.000.000
– Investasi 3 : butuh Rp 4.000.000 , akan berkembang mjd Rp
6.000.000
– Investasi 4 : butuh Rp 3.000.000 , akan berkembang mjd Rp
4.000.000
Capital Budgeting
•
•
•
•
•
•
•
Model IP : xi = investasi ke i , i=1,2,3,4
Xi = 0 jika tidak mengambil investasi i
= 1 jika mengambil investasi i
Maks : Z = 8x1 + 11x2 + 6x3 + 4x4
Kendala : 5x1 + 7x2 + 4x3 + 3x4 ≤ 14
xi  {0,1} , i = 1,2,3,4
( dalam juta rupiah )
Capital Budgeting
• Apabila ditambah kendala :
– Kita hanya dapat membuat paling banyak dua investasi
– Jika investasi 2 diambil, maka investasi 4 juga diambil
– Jika investasi 1 diambil, maka investasi 3 tidak dapat diambil
• Model matematikanya :
– ( x 1 + x2 + x 3 + x4 ≤ 2 )
– ( x 2 – x4 ≤ 0 )
– ( x 1 + x3 ≤ 1 )
Multiperiod Capital
Budgeting
• Dipunyai 3 jenis dana utk investasi sebesar Rp
14.000.000 , Rp 12.000.000 dan Rp 15.000.000
selama 4 periode.
• Kita identifikasi 4 kali kesempatan investasi :
• Investasi 1 : Rp 5.000.000 , Rp 8.000.000 dan Rp
2.000.000 dalam bln 1, bln 2, bln 3 akan menjadi Rp
8.000.000
• Investasi 2 : Rp 7.000.000 dan Rp 10.000.000 dalam
bln 1dan bln 3 akan menjadi Rp 11.000.000
Multiperiod Capital
Budgeting
• Investasi 3 : Rp 4.000.000 dan Rp 6.000.000 dalam bln
2 dan bln 3 akan menjadi Rp 6.000.000
• Investasi 4 : Rp 3.000.000 , Rp 4.000.000 dan Rp
5.000.000 dalam bln 1, bln 2, bln 3 akan menjadi Rp
5.000.000
• Bagaimana keputusan dari pemodal ?
Multiperiod Capital
Budgeting
• Model IP :
• Maks : Z = 8x1 + 11x2 + 6x3 + 5x4
• Kendala : 5x1 + 7x2
+ 3x4 ≤ 14
•
8x1
+ 4x3 + 4x4 ≤ 12
•
2x1 + 10x2 + 6x3 + 5x4 ≤ 15
•
xi  {0,1} , i = 1,2,3,4
•
( dalam juta rupiah )
Knapsack Problem
• Secara tradisional ada Knapsack ( karung /
tempat) dengan kapasitas 14.
• Ada sejumlah barang katakanlah 4 jenis barang.
Tiap barang mempunyai ukuran dan nilai , sbb :
Barang ke-
1
2
3
4
Ukuran
5
8
7
11
4
6
3
4
Nilai
• Tujuan : memaks. nilai total brg dlm knapsack !
Knapsack Problem
• Model IP :
• Maksimumkan :
•
Z = 8x1 + 11x2 + 6x3 + 4x4
• Kendala : 5x1 + 7x2 + 4x3 + 3x4 ≤ 14
•
xi  {0,1} , i = 1,2,3,4
•
Set Covering
• Amati masalah penempatan dalam suatu lokasi.
Suatu kota akan mempertimbang-kan lokasi
stasiun pemadam kebakaran.
• Stasiun pemadam kebakaran itu akan efektif bila
dia dapat menjangkau lokasi daerahnya sendiri
dan daerah tetangga sekitarnya yang
berbatasan.
• Tujuannya adalah meminimumkan banyak
stasiun pemadam kebakaran yang dibangun
serta dapat melayani semua daerah !
Set Covering
• Misal peta daerahnya adalah sbb :
Set Covering
• Model IP :
• Minimumkan :
• Z = x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11
• Kendala :
•
•
•
•
(1) x1+x2+x3+x4 ≥ 1
(2) x1+x2+x3+x5 ≥ 1
(3) x1+x2+x3+x4+x5+x6 ≥ 1
(4) x1+x3+x4+x6+x7 ≥ 1
Set Covering
•
•
•
•
•
•
•
•
(5) x2+x3+x5+x6+x8+x9 ≥ 1
(6) x3+x4+x5+x6+x7+x8 ≥ 1
(7) x4+x6+x7+x8 ≥ 1
(8) x5+x6+x7+x8+x9+x10 ≥ 1
(9) x5+x6+x8+x9+x10+x11 ≥ 1
(10) x8+x9+x10+x11 ≥ 1
(11) x9+x10+x11 ≥ 1
xi  {0,1} , i = 1,2,3, ….. ,11