5.2. Monte Carlo Untuk Menghitung Nilai p

5
.
M
O
N
T
E
C
A
R
L
O
5.1. Metode Monte Carlo
Metode pencarian acak adalah suatu metode dimana solusi dicari secara
acak dan diulang-ulang sampai dihasilkan solusi yang diharapkan.
Misalkan dicari suatu angka antara 0 sampai dengan 100, maka akan
diacak angka-angka antara 0 dan 100 sampai didapatkan angka yang
dimaksud. Metode ini tampak sangat sederhana, karena hanya
diperlukan bagaimana suatu solusi dinyatakan dan kemudian
mengacak nilainya hingga diperoleh nilai yang diharapkan dari model
solusi yang ada.
Metode pencarian acak ini menjadi tidak popular karena hasilnya
memang tidak bagus, tetapi sudah merupakan konsep dasar yang
menarik untuk dibahas. Ada beberapa hal yang perlu diperbaiki dari
konsep pencarian acak ini, antara lain:
Tidak semua nilai pada solusi harus diubah pada setiap iterasi. Bila sudah
solusi mendekati target tidak perlu perubahan yang terlalu besar.
Perlu pertimbangan bahwa munculnya bilangan acak sangat tergantung1
pada distribusi bilangan acak yang digunakan (lihat bab 4).
5 . 1 .
M e t o d e
M o n t e
C a r l o
Metode Monte Carlo memperbaiki metode pencarian acak ini dengan
mempertimbangkan kedua hal di atas, sehingga metode ini menjadi
metode simulasi yang banyak digunakan. Metode Monte Carlo
sebenarnya merupakan metode pencarian acak, tetapi dengan
beberapa perbaikan, yaitu: tidak semua nilai pada solusi diacak
ulang, tetapi dipilih satu nilai saja di antara barisan nilai solusi,
dan kemungkinan acak dari setiap kejadian solusi. Sebagai contoh,
pada pencarian kata setiap iterasi hanya mengubah satu nilai saja dari
kelima nilai yang ada dalam satu solusi. Bila pada solusi hanya
mengandung satu nilai saja maka metode Monte Carlo ini sama
dengan metode pencarian acak.
Beberapa impelementasi dasar dari Monte Carlo dalam proses simulasi
adalah sebagai berikut:
Metode Rejection pada pembangkitan bilangan acak yang berdistribusi
non-uniform seperti telah dibahas pada bab 4.
1. Menghitung nilai p.
2. Menghitung nilai integral
2
3. Pencarian Acak Dengan Monte Carlo
5.2. Monte Carlo Untuk Menghitung Nilai p
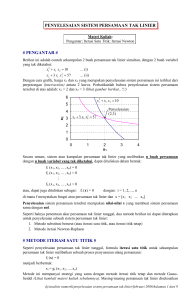
Perhatikan lingkaran dengan jari-jari 1, maka dapat dikatakan bahwa luas
lingkaran tersebut adalah p. Bila kita mengacak pasangan (x,y) dengan
bilangan acak [0,1] maka kita cukup memandang pada kuadran I pada
bujursangkar luar dari lingkaran berjari-jari 1 maka kemungkinan titik (x,y)
berada dalam lingkaran adalah:
1
-1
1
-1
3
5.2. Monte Carlo Untuk Menghitung Nilai p
Dengan kata lain bila dibangkitkan N pasang pasangan korrdinat (x,y)
dengan bilangan acak [0,1] maka ada m=Np/4 pasangan yang
berada dalam lingkaran pada kuadran I. Aturan ini bisa dikatakan
bahwa: nilai p dapat dihitung dengan:
4m
p 
N
dimana m adalah jumlah titik acak [0,1] yang masuk dalam lingkaran,
dan N adalah jumlah titik yang dibangkitkan.
dimana m adalah jumlah titik acak [0,1] yang masuk dalam lingkaran,
dan N adalah jumlah titik yang dibangkitkan.
Implementasi Monte Carlo untuk menghitung nilai p dalam MATLAB
adalah sebagai berikut:
4
5.2. Monte Carlo Untuk Menghitung Nilai p
% Memasukkan jumlah titik yang diacak
n=input('Jumlah titik acak = ');
% Mengacak n buah titik
x=rand(1,n);
y=rand(1,n);
% Menghitung jumlah titik
% yang masuk daerah lingkaran
p=(y<(1-x.^2).^0.5);
m=sum(p);
% Menghitung dan menampilkan nilai pi
mpi=4*m/n;
fprintf('pi = %1.5f\n',mpi);
Simpan dalam file hitungpi.m, kemudian jalankan program ini.
Beberapa hasil dari program ini adalah:
5
5.2. Monte Carlo Untuk Menghitung Nilai p
Jumlah titik acak = 10
Jumlah titik acak = 100
Jumlah titik acak = 1000
Jumlah titik acak = 2000
Jumlah titik acak = 2500
Jumlah titik acak = 4000
Jumlah titik acak = 10000
Jumlah titik acak = 20000
Jumlah titik acak = 50000
Jumlah titik acak = 100000
Jumlah titik acak = 250000
Jumlah titik acak = 500000
Jumlah titik acak = 1000000
pi = 3.20000
pi = 2.88000
pi = 3.15200
pi = 3.13800
pi = 3.11840
pi = 3.12800
pi = 3.15760
pi = 3.12640
pi = 3.13600
pi = 3.13876
pi = 3.14133
pi = 3.14120
pi = 3.14156
Memang dibutuhkan jumlah titik yang besar untuk dapat mendekati nilai
p yang sebenarnya. Tetapi ide ini merupakan ide dasar pencarian
yang sangat bagus.
6
5.3. Monte Carlo Untuk Menghitung Integral
Persoalan menghitung integral adalah persoalan dasar dalam kalkulus,
tetapi ternyata tidak semua fungsi dapat dihitung integralnya dengan
mudah. Metode Monte Carlo dapat digunakan untuk menghitung
integral dengan menghitung jumlah titik yang berada di dalam suatu
kawasan fungsi f(x) pada interval yang ditentukan.
7
5.3. Monte Carlo Untuk Menghitung Integral
Untuk menghitung integral f(x) dari [a,b] dengan menggunakan metode
Monte Carlo, maka dibangkitkan pasangan (x,y) secara acak dengan
nilai x=[a,b] dan nilai y=[0,1], Hitung jumlah titik (x,y) dimana y<f(x)
dengan f(x) didefinisikan
Nilai integral dapat dihitung dengan :
M
I
N
dimana :
M=jumlah titik yang terletak di dalam fungsi f(x)
N=jumlah titik yang dibangkitkan
8
5.3. Monte Carlo Untuk Menghitung Integral
Contoh 5.1.
Menghitung nilai:
1
 x.e
2 x
dx
0
Implementasi Monte Carlo untuk menghitung integral di atas dalam MATLAB
adalah:
% Memasukkan jumlah titik yang diacak
n=input('Jumlah titik acak = ');
% Mengacak n buah titik
x=rand(1,n);
y=rand(1,n);
% Menghitung jumlah titik
% yang masuk daerah integral fungsi
p=(y<x.*exp(-x));
m=sum(p);
% Menghitung dan menampilkan nilai integral
L=m/n;
fprintf('Integral = %1.5f\n',L);
9
5.3. Monte Carlo Untuk Menghitung Integral
Simpan dalam file integral1.m, kemudian jalankan. Salah satu contoh
hasilnya adalah sebagai berikut:
Jumlah titik acak = 10
Integral = 0.40000
Jumlah titik acak = 1000
Integral = 0.26800
Jumlah titik acak = 1500
Integral = 0.24800
Jumlah titik acak = 2000
Integral = 0.26950
Jumlah titik acak = 5000
Integral = 0.26440
Jumlah titik acak = 10000
Integral = 0.26470
Jumlah titik acak = 50000
Integral = 0.26316
Jumlah titik acak = 100000
Integral = 0.26270
Jumlah titik acak = 500000
Integral = 0.26416
Jumlah titik acak = 1000000
Integral = 0.26451
Hasil eksak dari nilai integral di atas adalah sebagai berikut:
1

 xe dx   xe  e
x
x
   e  e
x 1
0
1
1

 1  0.2642
0
10
5.4.
Pencarian
Acak
(Random
Walk)
Metode paling sederhana dalam menyelesaikan suatu
permasalahan tanpa harus melibatkan banyak
operasional matematis dan struktur data yang rumit
adalah metode pencarian secara acak, dimana suatu
penyelesaian diperoleh dengan mencoba-coba (trial and
error) dengan memanfaatkan bilangan acak. Misalkan
untuk mencari nilai terbesar dari f(x,y)=x*exp(-y) dapat
dihitung dengan mengacak pasangan nilai (x,y), dan
hitung nilai f(x,y), kemudian acak lagi pasangan nilai
(x,y) dan hitung nilai f(x,y), bila f(x,y) yang baru lebih
besar dicatat demikian seterusnya sehingga diperoleh
f(x,y) yang paling besar.
Algoritma dari pencarian acak untuk mencari nilai
maksimal suatu fungsi f(x) dari barisan nilai x=[xk 11
]
dapat dituliskan sebagai berikut:
5.4.
Pencarian
Acak
(Random
Walk)
• Acak satu penyelesaian x yang mungkin.
• Hitung nilai fungsi dari penyelesaian tersebut f(x)
anggap sebagai f_maksimal
• Acak lagi satu penyelesaian yang mungkin, dengan
mengubah satu atau beberapa bagian kejadian
pada ruang solusi.
• Hitung nilai fungsi dari penyelesaian tersebut f(x)
• Bila f(x)>f_maksimal maka f_maksimal=f(x)
• Ulangi langkah 2 sampai dinyatakan stop dengan
kriteria stop yang ditentukan. Kriteria stop yang
banyak dilakukan adalah jumlah iterasi atau nilai
maksimal acuan.
12
5.4.
Pencarian
Acak
(Random
Walk)
Contoh 5.1.
Mencari nilai maksimum dari fungsi:
dimana
0 x2
f ( x)  xe
Sebelum mencari penyelesaiannya
digambarkan fungsi ini dengan cara:
>> x=0:0.1:2;
>> y=x.*exp(-2*x);
>> plot(x,y), grid
2 x
sebaiknya
terlebih
dahulu
Dari grafik di atas, terlihat
bahwa nilai maksimum sekitar
0.18 sampai dengan 2, yang
terjadi di nilai x sekitar 0.4
sampai dengan 0.6.
Implementasi pencarian acak
dalam MATLAB untuk memperoleh nilai maksimum dari
fungsi f(x).
13
5.4.
Pencarian
Acak
(Random
Walk)
Contoh 5.1.
Mencari nilai maksimum dari fungsi:
dimana
0 x2
f ( x)  xe
Sebelum mencari penyelesaiannya
digambarkan fungsi ini dengan cara:
>> x=0:0.1:2;
>> y=x.*exp(-2*x);
>> plot(x,y), grid
2 x
sebaiknya
terlebih
dahulu
Dari grafik di atas, terlihat
bahwa nilai maksimum sekitar
0.18 sampai dengan 2, yang
terjadi di nilai x sekitar 0.4
sampai dengan 0.6.
Implementasi pencarian acak
dalam MATLAB untuk memperoleh nilai maksimum dari
fungsi f(x).
14
5.4.
Pencarian
Acak
% Memasukkan jumlah iterasi
n=input(‘Jumlah iterasi = ‘);
% Pengacakan nilai awal
x=rand;
y=x*exp(-2*x);
% Random walk dengan n iterasi
for iterasi=1:n
x1=rand;
y1=x1*exp(-2*x1);
if y1>y
x=x1;
y=y1;
end
end
% Hasil
fprintf('Iterasi %d : ',n);
fprintf('Nilai maksimum %1.3f ',y);
fprintf('terjadi di x = %1.3f\n',x);
(Random
Walk)
15
5.4.
Pencarian
Acak
(Random
Walk)
Simpan program ini dalam file rndwalk1.m, dan hasil dari
implementasi ini untuk setiap jumlah iterasi tertentu
adalah sebagai berikut:
Iterasi 10 : Nilai maksimum 0.184 terjadi di x = 0.500
Iterasi 50 : Nilai maksimum 0.184 terjadi di x = 0.499
Iterasi 100 : Nilai maksimum 0.184 terjadi di x = 0.499
Nilai maksimal yang diperoleh adalah 0.184.
Contoh 5.2.
Mencari kata acak sampai diperoleh kata yang disimpan
oleh komputer, misalkan kata acaknya adalah ‘STATE’.
Sebelumnya pastikan nilai target (kata yang disimpan)
dibentuk dalam array integer sehingga didefinisikan:
target = { 19 20 1 20 5 }, dimana nilai-nilai tersebut
menyatakan urutan dari alfabet pada kata target.
16
5.4.
Pencarian
Acak
(Random
Walk)
Implementasinya dalam bahasa MATLAB adalah:
% Menyimpan kata target
target=[19 20 1 20 5];
katatarget=char(target+64);
% Membuat kata secara acak
s=floor(rand(1,5)*26)+1;
% Menghitung jarak antara kata target dan s
e=sum(abs(target-s));
% Proses iterasi pencarian sebanyak 300 kali
for iterasi=1:300
% Menyimpan s ke dalam s1
s1=s;
% Melakukan update dengan mengubah
% salah satu huruf saja
17
5.4.
Pencarian
Acak
(Random
Walk)
k=floor(rand*5)+1;
s1(k)=floor(rand*26)+1;
% Menghitung jarak s1 dengan target
e1=sum(abs(target-s1));
% Menguji apakah s baru diterima
if(e1<=e)
s=s1;
e=e1;
end
% Setiap 20 iterasi ditampilkan
if mod(iterasi,25)==0
kata=char(s+64);
fprintf('Iterasi ke %d : %s\n',iterasi,kata);
end
end
18
5.4.
Pencarian
Acak
(Random
Walk)
Simpan dalam file carikata.m, lalu jalankan. Salah satu
hasilnya adalah sebagai berikut:
>> carikata
Iterasi ke 25 : VUJTC
Iterasi ke 50 : VUETC
Iterasi ke 75 : VUATE
Iterasi ke 100 : UTATE
Iterasi ke 125 : QTATE
Iterasi ke 150 : QTATE
Iterasi ke 175 : STATE
Iterasi ke 200 : STATE
Iterasi ke 225 : STATE
Iterasi ke 250 : STATE
Iterasi ke 275 : STATE
Iterasi ke 300 : STATE
19
5.4.
Pencarian
Acak
(Random
Walk)
Tugas 3.2.
1. Buat program sederhana dalam MATLAB untuk
meng-hitung nilai integral :


f ( x)  2 p e  x
untuk x = 0 s/d 1
2. Buatlah grafik yang menghubungkan jumlah titik yang
dibangkitkan dan nilai integral yang diperoleh.
20
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
Sampel data yang diperoleh dengan konfigurasi spin dari lattice
diletakkan pada suatu kesatuan. Kita pilih data yang mempunyai
bobot w,
we
 H i / Z
dimana Hi adalah energi pada konfigurasi i, teknik ini dinamakan
dengan algoritma Metropolis. Hal ini berguna untuk memilih
kandidat berikutnya pada proses pencarian acak (random walk),
dimana konfigurasi solusi yang dapat diterima adalah konfigurasi
solusi dengan bobot: H trial
e
w   H i
e
Bila proses ini dilakukan secara terus-menerus akan diperoleh kumpulan
data sampling yang mempunyai distribusi:
f ( Z )  e  H i / Z
21
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
Contoh 5.3.
Bangkitkan 10 bilangan acak [-1 1] yang menyatakan
komposisi elektron dari suatu atom. Misalkan:
S = [1 1 –1 1 –1 –1 –1 1 1 –1]
Energi yang terpancar dalam suatu komposisi elektron
adalah energi yang terjadi ketika terjadi dua kutub
yang berbeda yang berada secara berdampingan.
Energi untuk S dapat dihitung dengan:
S = [1 1 –1 1 –1 –1 –1 1 1 –1]
dE = [ 0 1 1 1 0 0 1 0 1 ]
Total Energi E=5.
Algoritma metropolis bersama-sama random walk dari
Monte Carlo akan mengubah komposisi di atas
menjadi komposisi dengan Energi yang minimum. 22
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
Proses 1:
Nomor state yang berubah = 3
S’ = [1 1 1 1 –1 –1 –1 1 1 –1]
dE’ = [ 0 0 0 1 0 0 1 0 1 ]
Total Energi E = 3
State ini diterima
Proses 2:
Nomor state yang berubah = 5
S’ = [1 1 1 1 1 –1 –1 1 1 –1]
dE’ = [ 0 0 0 0 1 0 1 0 1 ]
Total Energi E = 3
State ini diterima
Proses 3:
Nomor state yang berubah = 6
S’ = [1 1 1 1 –1 1 –1 1 1 –1]
dE’ = [ 0 0 0 1 1 1 1 0 1 ]
Total Energi E = 5
State ini tidak diterima
23
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
Proses di atas hanya melakukan pertimbangan perubahan state
dilakukan ketika energi lebih kecil. Perhatikan pada proses 1 dan
proses 2, meskipun kedua state ini berbeda tetapi energinya
sama. Hal ini membuat teknik perubahan state hanya dengan
pertimbangan besar-kecilnya energi masih terlalu dini untuk
dapat menyatakan kondisi terbaik.
Contoh Implementasi Algoritma Metropolis:
Algoritma metropolis untuk membangkitkan sejumlah bilangan acak xk
dengan distribusi f(xk).
1. Bangkitkan N pasangan bilangan acak (x,y)
2. Untuk Xn=xn Hitung ratio Metropolis dari masing-masing
pasangan
f ( y ) bilangan acak:
r
f ( x)
3. Tentukan
:
p  min(1, r)
 y dengan
xn 1  
dengan 1  p
x
24
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
Contoh 5.4.
Membangkitkan bilangan acak berdistribusi exponensial :
p( x) 
1
2 x
, e
0.4323
untuk 0 < x < 1
Implementasi Algoritma Metropolis untuk membangkitkan bilangan acak
dengan distribusi eksponensial di atas adalah sebagai berikut:
% Memasukkan jumlah bilangan acak
% yang akan dibangkitkan
n=input('Jumlah bilangan acak = ');
% Membangkitkan n pasangan bilangan acak (x,y)
for i=1:n
x=rand;
y=rand;
% Menghitung nilai ratio metropolis
fx=exp(-x)/0.4323;
fy=exp(-y)/0.4323;
r=fy./fx;
p=rand;
25
5 . 6 .
A l g o r i t m a
M e t r o p o l i s
if p<r
s(i)=y;
else
s(i)=x;
end
end
disp(s)
Simpan dalam file acakmet.m, kemudian jalankan.
Perhatikan hasil dari pembangkitan bilangan acak
dengan algoritma metropolis. Untuk membangkitkan
bilangan acak dengan fungsi distribusi yang berbeda,
tinggal mengganti fx dan fy pada program di atas.
26