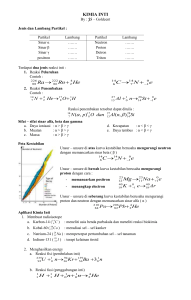
kajian stabilitas inti super berat dengan nomor

KAJIAN STABILITAS INTI SUPER BERAT DENGAN
NOMOR ATOM 110 SAMPAI DENGAN 200 MENGGUNAKAN
MODEL INTI TETESAN CAIRAN
AGIE MALIKI AKBAR
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2013
KAJIAN STABILITAS INTI SUPER BERAT DENGAN
NOMOR ATOM 110 SAMPAI DENGAN 200 MENGGUNAKAN
MODEL INTI TETESAN CAIRAN
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2013
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK
CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul “Kajian Stabilitas
Inti Super Berat dengan Nomor Atom 110 sampai dengan 200
Menggunakan Model Inti Tetesan Cairan” adalah benar karya saya dengan
arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun
kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau
dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis
lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di
bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada
Institut Pertanian Bogor.
Bogor, Maret 2013
Agie Maliki Akbar
NIM G74090021
ABSTRAK
AGIE MALIKI AKBAR. Kajian Stabilitas Inti Super Berat dengan Nomor
Atom 110 sampai dengan 200 Menggunakan Model Inti Tetesan Cairan.
Dibimbing oleh ABD. DJAMIL HUSIN.
Model inti tetesan cairan dapat digunakan untuk menduga energi
ikat, energi ikat per nukleon, isotop paling stabil, dan kondisi terjadinya fisi
spontan. Persamaan-persamaan tersebut kemudian diubah menjadi bentuk
persamaan numerik yang kemudian dimasukkan ke dalam bahasa
pemrograman MATLAB.
Berdasarkan hasil perhitungan yang telah
dilakukan pada penelitian ini, inti super berat akan mengalami fisi spontan
di atas Z = 135. Pada Z = 135 energi yang diperlukan untuk membuat inti
mengalami fisi atau energi aktivasi sangat kecil yaitu sekitar 0.48 MeV. Di
atas Z = 135 energi aktivasi adalah negatif, artinya untuk membentuk inti
dengan Z > 135 diperlukan sejumlah energi. Kemudian pada Z = 135 rasio
Z2/A adalah 48.86, hampir mencapai syarat rasio Z2/A dimana inti akan
mengalami fisi spontan yaitu 49. Energi ikat per nukleon untuk inti-inti
super berat sampai Z = 200 adalah sekitar 7 – 5.5 MeV, sama dengan
kisaran inti-inti ringan yang stabil. Sehingga kemungkinan terdapat inti-inti
super berat yang stabil di Z < 135 dan di atas Z > 135 tidak akan terdapat
inti yang stabil.
Kata kunci : inti super berat, fisi spontan, energi aktivasi, energi ikat per
nukleon, pairing
ABSTRACT
AGIE MALIKI AKBAR. Super Heavy Nucleic Stability Review with
Atomic Numbers 110 to 200 Using the Liquid Droplets Model Nucleic.
Guided by ABD. DJAMIL HUSIN.
Liquid droplets of nucleic models can be derived equations to
estimate the binding energy, binding energy per nucleon, the most stable
isotope, and the condition of the occurrence of spontaneous fission. The
equations are then converted into a numerical equation form which is then
inserted into the MATLAB programming language. Based on the results of
the calculations have been carried out in this study, super-heavy nuclei will
undergo spontaneous fission in the Z = 135. At Z = 135 the energy needed
to create the nucleus undergoing fission or activation energy is very small at
around 0:48 MeV. Above Z = 135 the activation energy is negative, it
means to form a nucleus with Z> 135 needed some energy. Then at Z = 135
the ratio Z2 / A is 48.86, almost reaching requirement ratio Z2 / A where the
nucleic will undergo spontaneous fission is 49. Binding energy per nucleon
for super-heavy nuclei up to Z = 200 is about 7 - 5.5 MeV, together with a
range of light nuclei are stable. So there may be a super-heavy nuclei are
stable at Z <135 and above Z> 135 there will be no stable nucleic
Keywords: super heavy nuclei, spontaneous fission, activation energy,
binding energy per nucleon, pairing
KAJIAN STABILITAS INTI SUPER BERAT DENGAN
NOMOR ATOM 110 SAMPAI DENGAN 200 MENGGUNAKAN
MODEL INTI TETESAN CAIRAN
AGIE MALIKI AKBAR
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains
pada
Departemen Fisika
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2013
Juclu\ Skripsi : Kajian Stabilitas Inti Super Bcr;lt dCI1gt1l1 Nomor Atom 110
Sampai dengan 200 Menggul1<1bl1 \ 'loc1el Inti Tetesan Cairan
:
Agie Maliki Akbar
Nama
: 074090021
NIM
Disetujui oleh
Abd. Djamil Husin, M.Si Pembimbing Diketahui oleh Tanggal Lulus:.
B JUL 2013
Judul Skripsi : Kajian Stabilitas Inti Super Berat dengan Nomor Atom 110
Sampai dengan 200 Menggunakan Model Inti Tetesan Cairan
Nama
: Agie Maliki Akbar
NIM
: G74090021
Disetujui oleh
Abd. Djamil Husin, M.Si
Pembimbing
Diketahui oleh
h
Dr. Akhiruddin Maddu, M.Si
Ketua Departemen Fisika
Tanggal Lulus:
PRAKATA
Puji syukur kami sampaikan kepada Allah SWT yang telah
memberikan rahmat-Nya sehingga kami mampu menyelesaikan usulan
penelitian yang berjudul “Kajian Stabilitas Inti Super Berat dengan Nomor
Atom 110 sampai dengan 200 Menggunakan Model Inti Tetesan Cairan”.
Shalawat dan salam semoga senantiasa tercurah pula kepada Rasulullah
Muhammad SAW serta para sahabatnya. Teriring doa dan harap semoga
Allah SWT meridhoi upaya yang kami lakukan.
Usulan penelitian ini ditujukan sebagai salah satu syarat untuk
melaksanakan penelitian pada Departemen Fisika, Fakultas Matematika dan
Ilmu Pengetahuan Alam, Institut Pertanian Bogor. Penulis mengucapkan
terimakasih kepada berbagai pihak yang telah membantu dalam menyusun
usulan penelitian ini, terutama kepada Abdul Djamil Husin sebagai dosen
pembimbing yang telah banyak memberikan bimbingan dan arahan kepada
penulis dalam penyusun usulan penelitian ini. Besar harapan penulis karya
ini dapat bermanfaat bagi penulis maupun masyarakat dalam bidang sains
terutama bidang fisika nuklir.
Bogor, Maret 2013
Agie Maliki Akbar
DAFTAR ISI
DAFTAR GAMBAR
v
DAFTAR LAMPIRAN
vi
PENDAHULUAN
1
Latar Belakang
1
Perumusan Masalah
2
Tujuan Penelitian
2
Manfaat Penelitian
3
Ruang Lingkup Penelitian
3
TINJAUAN PUSTAKA
3
Model Inti Tetesan Cairan
METODE
3
7
Waktu dan Tempat Penelitian
7
Prosedur Penelitian
7
Tinjauan Pustaka
7
Melakukan Simulasi Perhitungan Energi Kestabilan Inti
7
Analisis Hasil Kajian
8
HASIL DAN PEMBAHASAN
SIMPULAN DAN SARAN
8
17
Simpulan
17
Saran
17
DAFTAR PUSTAKA
18
LAMPIRAN
19
RIWAYAT HIDUP
26
DAFTAR GAMBAR
1 Diagram alir simulasi
2 Grafik hubungan energi ikat per nukleon terhadap nomor massa untuk
inti-inti ringan dan inti-inti sedang
3 Grafik hubungan energi ikat per nukleon terhadap nomor massa untuk
inti-inti berat
4 Grafik hubungan energi ikat per nukleon terhadap nomor massa untuk
inti-inti super berat
5 Grafik hubungan jumlah neutron terhadap jumlah neutron
6 Grafik hubungan energi total yang dilepas ketika terjadi fisi dan energi
8
10
11
12
14
7 Grafik hubungan energi aktivasi terhadap nomor massa estimasi
16
DAFTAR LAMPIRAN
1 Program untuk menduga energi ikat, energi ikat per nukleon, mencari
isotop paling stabil, syarat terjadinya fisi spontan, dan energi aktivasi
19
1
PENDAHULUAN
Unsur dengan nomor atom terbesar yang terbentuk secara alami
adalah uranium. Unsur-unsur setelah uranium semuanya bersifat radioaktif
dan mempunyai kestabilan yang relatif rendah. Oleh karena itu unsur-unsur
tersebut kelimpahannya di alam sangat sedikit (atau bahkan tidak terdapat di
alam), tetapi dapat dihasilkan di laboratorium. Unsur-unsur setelah uranium
ini disebut unsur transuranik yang deretnya diawali oleh neptunium (Z =
93). Proses pembentukan unsur transuranik ini mengikuti proses
penangkapan neutron yang disusul oleh peluruhan beta. Dengan proses
tersebut sampai saat ini nomor atom unsur paling besar yang berhasil
dibentuk adalah
.6 Untuk menghasilkan inti dengan nomor atom di
atas 107 metode tangkapan neutron tidak dapat lagi digunakan karena waktu
yang paruh yang sangat singkat dari inti-inti transuranik. Inti-inti
selanjutnya dapat dihasilkan dengan cara menembak sebuah inti berat
dengan sebuah inti sedang. Dengan cara ini unsur dengan nomor atom
paling besar yang berhasil dibentuk adalah
.
Sampai saat ini isotop unsur-unsur transuranik yang berhasil
dihasilkan mempunyai waktu paruh beberapa menit atau detik saja.6 Terlihat
jelas waktu paruh yang sangat singkat dari unsur-unsur transuranik
disebabkan akibat bertambahnya gaya tolak Coulomb seiring bertambahnya
nomor atom Z. Untuk mencapai kestabilan unsur-unsur ini mengalami
peluruhan beta, alfa, atau membelah secara spontan (fisi spontan). Tetapi
pada 1960-an Glenn T. Seaborg menyatakan bahwa kemungkinan terdapat
daerah dimana ada isotop inti-inti super berat yang stabil. Daerah tersebut
dinamakan island of stability. Dasar dari pernyataan ini berasal dari model
inti kulit yang menyatakan konfigurasi pengisian nukleon pada inti analog
dengan pengisian elektron pada atom. Menurut perhitungan yang rumit
tentang struktur inti, unsur-unsur dengan nomor atom 111, 112, 113, 114
haruslah stabil terhadap peluruhan beta, alfa, atau fisi spontan.3 Penelitian
ini bertujuan meninjau kestabilan inti-inti tersebut melalui model inti yang
lain yang sebetulnya berlawanan dengan model inti kulit yaitu model inti
tetesan cairan. Jika model inti kulit memperlakukan nukleon-nukleon pada
inti secara sendiri-sendiri (independen), sedangkan model inti tetesan cairan
memperlakukan nukleon-nukleon pada inti seperti satu kesatuan (kolektif).
Latar Belakang
Seiring bertambahnya nomor atom Z gaya tolak Coulomb akibat
interaksi antar proton semakin kuat, sehingga semakin menurunkan
kestabilan inti. Pada inti-inti berat gaya tolak Coulomb karena jumlah
proton di dalam inti semakin banyak. Pada inti-inti berat dengan nomor
atom Z yang besar, gaya tolakan Coulomb yang kuat akibat banyaknya
2
proton diimbangi oleh jumlah neutron yang besar sekitar 1.6 kali jumlah
proton. Jumlah neutron yang lebih banyak dibandingkan jumlah proton
membuat gaya kuat akibat interaksi neutron-neutron dan neutron-proton
semakin kuat sehingga mampu mengimbangi gaya tolak Coulomb akibat
interaksi proton-proton. Peningkatan interaksi kuat hanya bertambah secara
linier seiring dengan kenaikan jumlah neutron N, sedangkan gaya tolak
Coulomb meningkat secara kuadratik dengan bertambahnya Z sehingga
akan ada kondisi dimana sebuah gaya kuat yang mengikat inti tidak mampu
lagi mengimbangi gaya tolak Coulomb sehingga inti akan membelah,
kondisi ini disebut fisi spontan. Pada fisi spontan sebuah inti akan
membelah menjadi dua atau lebih yang bermassa lebih ringan dengan
sendirinya tanpa harus dipicu oleh partikel penembak. Berbeda dengan
proses fisi pada umumnya yang membutuhkan partikel penembak agar
proses fisi bisa terjadi. Model inti tetesan cairan dapat digunakan untuk
menduga kapan kondisi ini bisa terjadi.
Perumusan Masalah
1.
2.
3.
Bagaimanakah kestabilan suatu inti atom jika inti tersebut
mempunyai nomor atom dan nomor massa sangat besar.
Sampai di nomor massa berapakah inti akan mengalami fisi spontan?
Adakah inti super berat yang stabil?
Tujuan Penelitian
1.
2.
3.
4.
5.
Mengkaji kestabilan inti super berat menggunakan model inti tetesan
cairan.
Menduga isotop paling stabil inti-inti super berat.
Menghitung energi ikat per nukleon inti-inti super berat.
Menghitung dan memperkirakan energi aktivasi inti-inti super berat.
Menghitung rasio Z2/A dan energi aktivasi untuk menduga di nomor
atom berapakah inti super berat akan mengalami fisi spontan.
3
Manfaat Penelitian
Manfaat dari penelitian ini adalah untuk memprediksi kestabilan intiinti super berat, memprediksi nomor massa dan jumlah neutron-proton pada
inti-inti berat yang stabil sehingga memberikan referensi bagi para ilmuwan
dalam proses pembentukan inti-inti super berat yang stabil.
Ruang Lingkup Penelitian
Pada kajian ini diasumsikan bahwa inti mengalami fisi spontan
dengan distribusi massa sama besar. Artinya inti membelah menjadi dua
buah inti baru yang bermassa hampir sama. Kemudian efek kuantum yang
dilibatkan pada penelitian ini hanya efek pairing pengisian tingkat energi
nukleon saja. Bilangan-bilangan ajaib yang diperoleh dari model kulit yang
disinggung pada penelitian ini hanya sebagai pembanding saja, tidak
dibahas lebih lanjut tentang asal-usulnya. Penelitian ini sepenuhnya
menggunakan model inti tetesan cairan.
TINJAUAN PUSTAKA
Model Inti Tetesan Cairan
Von Wieszacker pada tahun 1935 mendapati bahwa sifat-sifat inti
berhubungan dengan ukuran, massa, dan energi ikat mirip dengan apa yang
dijumpai di dalam tetesan cairan. Kerapatan tetesan cairan adalah konstan,
ukurannya sebanding dengan jumlah partikel atau molekul di dalam cairan,
penguapan panas atau energi ikatnya berbanding lurus dengan massa atau
jumlah partikel yang membentuk tetesan.
Energi ikat menurut model inti tetesan cairan dinyatakan oleh :
(
)
(
)
(1)
Konstanta pada Persamaan 1 ditentukan dari data eksperimen.
Nilainya (dalam satuan energi) yang dapat diambil adalah
= 14 MeV,
= 13 MeV,
= 0.6 MeV, = 19 MeV dan untuk
bernilai -33.5 MeV
4
jika inti mempunyai A genap dan Z genap, bernilai 0 jika A ganjil dan
bernilai +33.5 MeV jika A ganjil dan Z ganjil.
Asumsi dari model ini adalah menggangap inti seperti tetesan cairan,
dimana energi yang dibutuhkan untuk menguapkan tetesan cairan sebanding
dengan jumlah molekul di dalam cairan tersebut yang berarti energi ikatnya
sebanding dengan jumlah molekul yang terkandung pada cairan tersebut.
Pada inti juga dianggap demikian sehingga menghasilkan suku pertama
pada Persamaan 1 yaitu
yang menyatakan energi volume. Selanjutnya
energi volume ini dikoreksi oleh kenyataan bahwa nukleon-nukleon yang
terletak pada permukaan inti kurang terikat dibanding dengan nukleon yang
berada di lebih dalam. Koreksi ini sebanding dengan luas permukaan inti
tersebut, menghasilkan koreksi permukaan
. Keberadaan proton di
dalam inti menyebabkan energi ikat berkurang karena adanya gaya
Coulomb antar proton yang saling tolak menolak. Untuk itu perlu
ditambahkan suku koreksi akibat adanya interaksi Coulomb antar proton
(
)
yaitu
yang besarnya tergantung dari jumlah proton yang
berinteraksi.2 Rumus energi ikat di atas dapat diperbaiki dengan dengan
memasukan dua efek yang sebenarnya tidak cocok dengan model tetesan
cairan sederhana tetapi bisa diterangkan dalam model yang menghasilkan
tingkat energi. Salah satu efek ini terjadi jika jumlah neutron dalam inti
melebihi jumlah proton (atau sebaliknya), ini berarti tingkat energi yang
lebih tinggi harus terisi, sedangkan hal itu tidak terjadi jika N dan Z sama
sehingga menghasilkan koreksi asimetri (
)
. Sedangkan efek
yang kedua adalah terjadi akibat adanya kecenderungan terjadi pasangan
proton dan pasangan neutron, sehingga inti genap-genap merupakan inti
termantap, sehingga mempunyai energi ikat lebih tinggi daripada yang
diharapkan. Jadi inti seperti
dan
muncul sebagai puncak dalam
kurva empiris energi ikat per nukleon. Pada ekstrim lain, inti ganjil-ganjil
memiliki proton tak berpasangan dan neutron tak berpasangan dan memiliki
energi ikat yang relatif rendah.1 Energi pasangan bernilai positif untuk inti
genap-genap dan inti genap-ganjil dan bernilai negatif untuk inti ganjilganjil dan berubah terhadap A menurut A-3/4. Sehingga menghasilkan
koreksi energi pasangan A-3/4.1
Model inti tetesan cairan dapat digunakan untuk menduga kondisi
terjadinya fisi spontan. Persamaan energi ikat inti
secara umum
(
)
(
)
(
)
(2)
maka dengan mensubstitusikan Persamaan 1 ke dalam Persamaan 2 dapat
(
).
diperoleh perumusan massa semi empirik
(
)
(
)
(
)
(3)
Dengan
bernilai -33.5 MeV untuk inti dengan nomor massa A dan
nomor atom Z genap dan bernilai +33.5 MeV untuk inti dengan nomor
massa dan nomor atom ganjil.
5
kemudian dengan mengatur ulang Persamaan diatas diperoleh Persamaan
(
)
(
)
(4)
dengan
γ
+
β
α
Persamaan 3 merupakan Persamaan parabolik, dimana titik balik minimum
Zo diberikan oleh
|
(
(
))
| = 0 dengan A konstan
Diperoleh
(nomor atom untuk isobar paling stabil)
(5)
Persamaan diatas merupakan Persamaan untuk menduga isobar (inti dengan
nomor massa A sama, tapi nomor atom Z berbeda) paling stabil Zo untuk
nomor massa A tertentu. Karena nilai Z adalah suatu bilangan bulat yang
berurutan maka dengan memasukan nilai Z tersebut dapat di duga isotop
untuk tiap nomor atom Z. Kemudian setiap nomor massa tiap isotop
dimasukan ke Persamaan 1 untuk memperoleh isotop yang paling stabil.
Batas terjadinya fisi spontan dapat diturunkan dari Persamaan 1. Fisi
spontan terjadi akibat adanya perubahan koreksi energi Coulomb dan
koreksi energi permukaan akibat berubahnya bentuk inti. Dengan adalah
eksentrisitas inti yang berhubungan dengan parameter deformasi β.
( )
(
(
)
)
(
)
Perubahan energi ikat akibat deformasi dinyatakan oleh
(
)
(6)
6
Dengan
adalah eksentrisitas inti yang berhubungan dengan parameter
deformasi β. Eksentritas inti dinyatakan oleh
. Dengan
√
parameter deformasi dinyatakan oleh
√
(7)
dimana
adalah perbedaan antara sumbu semi mayor dan sumbu semi
minor. Dan
adalah jari-jari inti rata-rata didekati oleh Persamaan
. Jika suku kedua lebih besar dari suku pertama, perubahan
energi positif dan diperoleh peningkatan energi melalui perubahan bentuk
inti. Semakin lonjong inti, semakin besar energi yang diperoleh. Syarat
terjadinya fisi spontan adalah
dan
dan dengan memasukan nilai
syarat terjadinya fisi spontan terjadinya jika
didapatkan
(8)
Selain dapat digunakan untuk menduga kondisi terjadinya fisi
spontan model inti tetesan cairan juga dapat digunakan untuk menduga
energi aktivasi yang diperlukan untuk mengakibatkan terjadinya fisi. Jika
diasumsikan ketika fisi inti terbelah menjadi dua inti yang identik maka
energi potensial Coulomb
yang menghalangi terjadi proses fisi
dinyatakan oleh
(
)
(9)
dengan
Z1, Z2 = jumlah proton inti akhir masing-masing
R1, R2 = jari-jari inti akhir masing-masing
e = muatan proton (1.6 x 10-19 C)
Seperti pada proses peluruhan α dan β, proses fisi spontan yang
terjadi pada inti berat adalah salah satu cara inti menuju kestabilan. Oleh
karena itu inti akhir dari proses fisi spontan ini harus lebih stabil dari inti
awalnya. Misal, energi ikat inti pada daerah inti-inti berat adalah sekitar 7.6
MeV. Jika sebuah inti
membelah menjadi dua buah inti dengan massa
masing-masing 119, dengan energi ikat per nukleonnya sekitar 8.5 MeV.
Energi ikat inti akhir yang lebih besar dari inti awal mengharuskan
sejumlah energi harus dilepaskan. Energi yang dilepaskan adalah perubahan
energi ikat inti awal dan inti akhir. Perubahan energi ikat yang terjadi adalah
: energi ikat inti
adalah 238 x -7.6 MeV = -1809 MeV kemudian jika
inti tersebut membelah menjadi dua buah inti
maka energi ikat inti
7
akhir adalah sebesar 2 x 119 x -8.5 = -2033 MeV. Keadaan akhir dari
proses tersebut mengandung kelebihan energi sebesar ΔEf = 214 MeV yang
dapat muncul dalam berbagai bentuk (energi neutron, energi peluruhan β,
dan emisi sinar γ). Tetapi sekitar 80% dari energi ini digunakan sebagai
energi kinetik kedua inti akhir.7 Energi total Et yang terjadi selama fisi
adalah perubahan energi akibat deformasi ΔEd ditambah dengan perubahan
energi ikat inti setelah inti mengalami fisi ΔEf.. Jika energi total ini lebih
besar dibanding energi potensial halangan Coulomb
maka inti akan
mengalami fisi spontan. Energi aktivasi diberikan oleh
(10)
METODE
Waktu dan Tempat Penelitian
Penelitian ini dilaksanakan pada bulan Februari 2013 sampai bulan
Juli 2013. Tempat penelitian dilakukan di laboratorium Fisika Teori dan
Komputasi, Departemen Fisika, Fakultas Matematika dan Ilmu Pengetahuan
Alam, Institut Pertanian Bogor.
Prosedur Penelitian
Studi Pustaka
Sebelum melaksanakan penelitian ini, penulis melakukan studi
pustaka mengenai model inti tetesan cairan. Selain itu penulis juga
melakukan studi pustaka mengenai faktor-faktor yang mempengaruhi
stabilitas inti yaitu energi ikat, energi ikat per nukleon, rasio jumlah neutron
dan proton, eksentrisitas inti, dan efek pasangan (pairing).
Melakukan Simulasi Perhitungan Energi Kestabilan Inti
Kajian dilakukan dengan menggunakan Persamaan energi ikat
menurut model inti tetesan cairan (Persamaan 1). Dari Persamaan 1 dapat
diturunkan berbagai Persamaan untuk menduga kestabilan inti. Diantaranya
energi ikat, energi ikat per nukleon, energi aktivasi, dan kondisi terjadinya
fisi spontan. Persamaan-Persamaan turunan tersebut kemudian diubah ke
dalam bentuk Persamaan numerik lalu dimasukkan ke dalam software
8
MATLAB R2008b untuk diolah lebih lanjut. Urutan simulasi penelitian
disajikan oleh gambar dibawah.
Persamaan energi ikat per nukleon model
inti tetesan cairan
(Persamaan 1)
Persamaan untuk
mencari isobar paling
stabil
Masukkan nilai A = 1,
2, 3, 4... dst
untuk menduga
kombinasi Z dan A
yang paling stabil
Persamaan perubahan
energi ikat akibat
deformasi
Syarat terjadinya fisi
spontan
Persamaan Potensial
Coulomb
Energi aktivasi
Kombinasi Z dan A
yang paling stabil dan
energi ikatnya
Daerah inti-inti super berat
yang diduga stabil
Gambar 1. Diagram alir simulasi. Garis merah menunjukkan input berupa Z
dan A, garis hijau menunjukkan ouput berupa energi, dan garis
hitam ouput berupa rasio.
9
Analisis Hasil Simulasi
Setelah melakukan simulasi, penulis kemudian menganalisis hasil
simulasi untuk memprediksi kemungkinan adanya inti super berat yang
stabil. Aspek kestabilan yang menjadi fokus kajian adalah energi ikat per
nukleon, rasio jumlah neutron terhadap proton, dan efek pairing.
HASIL DAN PEMBAHASAN
Kestabilan sebuah inti atom ditentukan oleh berbagai faktor, antara
lain oleh energi ikat per nukleon, rasio jumlah proton-neutron, dan efek
pasangan (pairing) antar nukleon. Semakin besar nomor atom, energi ikat
inti cenderung semakin meningkat karena diketahui bahwa gaya kuat yang
mengikat nukleon-nukleon di dalam inti berjangkauan pendek, dan sebuah
nukleon hanya berinteraksi dengan tetangga terdekatnya, sehingga energi
yang dibutuhkan untuk memecah sebuah inti sebanding dengan jumlah
nukleonnya. Tetapi karena di dalam inti terdapat proton maka interaksi
Coulomb antar proton menyebabkan energi ikat inti akan terkoreksi. Untuk
inti-inti ringan dengan nomor massa kurang dari 20, koreksi energi ikat
akibat interaksi Coulomb tidak terlalu berpengaruh karena pada inti-inti
ringan jumlah proton yang terkandung relatif sedikit dan jumlah neutron
dan protonnya relatif sama. Nukleon yang berspin ½ mengikuti prinsip
ekslusi Pauli sehingga setiap tingkat energi inti dapat mengandung dua
neutron yang berspin berlawanan dan dua proton yang berspin berlawanan.1
Tingkat energi dalam inti diisi menurut aturan tertentu sama dengan tingkat
energi pada atom, agar terjadi suatu konfigurasi dengan energi paling
minimum sehingga mempunyai kestabilan maksimum, sehingga jumlah
proton dan neutron yang sama memungkinkan terjadinya pairing yang
menurunkan energi total inti. Proton dan neutron di orbit yang sama akan
cenderung berpasangan (pairing) untuk membentuk keadaan momentum
anguler, J = 0, sedangkan jika sebuah inti mempunyai proton atau neutron
ganjil, total momentum angulernya adalah momentum anguler nukleon
terakhir (ganjil). Selain itu karena jumlah proton dan neutron relatif sama
menyebabkan neutron dan proton dapat menempati tingkat energi paling
rendah yang tersedia.1
Unsur alami dengan nomor atom di atas Bismut sampai Uranium
semuanya diamati bersifat radioaktif (mengalami peluruhan beta atau alfa)
dengan waktu paruh yang bervariasi dari 0,0018 detik untuk
sampai
1,39 x 1010 tahun untuk
.2 Sampai saat ini tidak ditemukan inti di atas
yang stabil terhadap peluruhan beta atau alfa. Sedangkan inti berat
dengan nomor massa paling tinggi yang terbentuk secara alami di alam
adalah uranium. Tidak ada inti dengan nomor atom di atas uranium yang
terbentuk secara alami, karena waktu paruh yang singkat dari inti-inti berat
menyebabkan proses tangkapan neutron secara alami tidak lagi berpeluang
10
menghasilkan inti-inti baru. Tetapi inti-inti setelah uranium dapat dihasilkan
di laboratorium. Proses pembentukkan deret unsur yang diawali dengan
neptunium (Z = 93) yang disebut unsur-unsur transuranik, melalui proses
penangkapan neutron disusul dengan peluruhan beta. Dengan cara ini semua
unsur hingga Z = 107 dihasilkan.6 Sebagian besar unsur dalam deret ini
mempunyai waktu paruh beberapa menit atau beberapa detik saja yang
artinya inti-inti tersebut mempunyai kestabilan yang rendah. Gambar 2
memperlihatkan hubungan antara energi ikat per nukleon terhadap nomor
massa untuk inti-inti ringan dan inti-inti sedang. Terlihat bahwa untuk intiinti dengan Z genap dan N genap mempunyai energi ikat per nukleon lebih
besar dari inti-inti sekitarnya. Hal ini menunjukkan kuatnya efek pairing
yang terjadi pada inti-inti ringan dan inti-inti sedang. Hal ini berbeda pada
wilayah dengan A > 150 (inti-inti berat). Di sini efek pairing mulai
menghilang dan energi ikat per nukleon inti cenderung terus menurun. Hal
ini menunjukkan bahwa untuk inti-inti berat koreksi akibat tolakan Coulomb
dan koreksi akibat ketidaksimetrian antara jumlah proton dan jumlah
neutron mulai mendominasi.
Salah satu ciri dari inti-inti berat adalah berlebihnya jumlah neutron
dibanding proton. Di satu sisi jumlah neutron yang berlebih diharapkan
dapat mengimbangi gaya tolak antar proton, tetapi di sisi lain berlebihnya
jumlah neutron terhadap proton mengharuskan neutron tambahan
menempati tingkat energi yang lebih tinggi dibanding proton. Jika kita
analogikan dengan elektron pada atom, semakin tinggi tingkat energi
semakin kecil energi ikat, sehingga kemungkinan neutron untuk terlepas
atau meluruh menjadi proton lebih besar dibanding neutron yang menempati
Gambar 2. Grafik hubungan energi ikat per nukleon terhadap nomor massa
untuk inti-inti ringan dan inti-inti sedang
11
tingkat energi yang lebih rendah. Berdasarkan hasil perhitungan diketahui
untuk inti-inti super berat (inti-inti dengan nomor atom Z > 110) rasio
neutron terhadap proton mencapai 1.7 ~ 2. Gambar 3 memperlihatkan
bahwa pada daerah inti-inti berat terlihat bahwa semakin besar nomor atom
dan nomor massa energi ikat per nukleon cenderung terus mengalami
penurunan, tidak ditemukan inti yang mempunyai energi ikat per nukleon
lebih besar dibanding inti-inti tetangganya. Kondisi ini berlanjut pada intiinti super berat. Sehingga sangat sulit untuk menentukkan inti-inti berat
yang kemungkinan stabil hanya berdasarkan energi ikat per nukleonnya
saja. Gambar 4 menunjukkan hubungan antara energi ikat per nukleon
terhadap nomor massa untuk inti-inti super berat. Cara yang dapat
digunakan untuk menduga kestabilan pada inti-inti super berat adalah
dengan melihat pengisian nukleon terluar di luar closed shell (jumlah
nukleon yang memenuhi bilangan ajaib). Jika kita lihat pada kasus inti-inti
ringan dan inti-inti sedang, inti-inti yang mempunyai jumlah nukleon terluar
sama dengan salah satu bilangan ajaib atau berjumlah genap mempunyai
kestabilan lebih tinggi dibanding inti-inti sekitarnya. Jika hal ini juga
berlaku pada inti-inti super berat maka dapat diduga inti-inti super berat
dengan nomor atom 111, 112, 113, 114, 126, 142, 143, dan 144 akan
mempunyai kestabilan yang lebih tinggi dibanding inti-inti disekitarnya
karena inti-inti tersebut di prediksi mempunyai jumlah neutron sama dengan
bilangan ajaib untuk neutron yaitu 184 (untuk inti dengan Z = 111, 112,
113) dan 258 (untuk inti dengan nomor atom (142, 143, dan 144) dan
bilangan ajaib untuk proton 126 (untuk inti dengan Z = 126).
Gambar 3. Grafik hubungan energi ikat per nukleon terhadap nomor massa
untuk inti-inti berat
12
Gambar 4. Grafik hubungan energi ikat per nukleon terhadap nomor massa
untuk inti-inti super berat
Berdasarkan hasil perhitungan yang dilakukan pada penelitian intiinti tersebut mempunyai energi ikat per nukleon yang cukup besar, sekitar
6.8 sampai 7 MeV, sehingga dapat diduga inti-inti tersebut akan stabil,
mengingat inti-inti isotop inti-inti ringan yang stabil seperti
dan
mempunyai energi per nukleon yang berada pada kisaran yang sama. Tetapi
kenyataannya hasil eksperimen menunjukkan bahwa salah satu isotop intiinti transuranik
,
,
,
yang berhasil dibuat
mempunyai waktu paruh yang sangat singkat dengan orde beberapa
milisekon sampai beberapa sekon. Waktu paruh yang singkat menunjukkan
bahwa inti-inti tersebut mempunyai kestabilan yang rendah yang tidak
sesuai dengan dugaan model inti kulit. Tetapi walaupun demikian belum
dapat dipastikan inti-inti dengan nomor atom di atas benar-benar tidak stabil
karena sejauh ini baru satu isotop yang berhasil dihasilkan. Sebagai contoh
salah isotop inti
yang berhasil diciptakan di laboratorium Society of
Heavy Ion Research di Darmstad, Jerman memiliki nomor massa 285 dan
memiliki paruh sekitar 29 detik. Sedangkan hasil perhitungan menggunakan
model inti tetesan cairan yang dilakukan pada penelitian ini menunjukkan
bahwa
adalah isotop paling stabil untuk inti
dengan energi ikat
per nukleon sekitar 7,15 MeV. Untuk membentuk inti-inti di atas proses
penangkapan neutron dan peluruhan beta tidak dapat lagi digunakan karena
tidak tersedia neutron yang cukup untuk memasok neutron yang diperlukan
untuk kestabilan. Dengan demikian perlu digunakan inti yang kaya akan
neutron sebagai proyektil sasaran, seperti
+
, dengan harapan bahwa
suatu keadaan antara (semacam inti gabung) akan terbentuk yang kemudian
meluruh (atau mungkin berfisi) ke isotop stabil pada Z = 112 misalnya 3.
13
Interaksi Coulomb akibat adanya kehadiran proton bertambah secara
kuadratik dengan meningkatnya Z sedangkan interaksi kuat hanya
meningkat secara linier seiring dengan meningkatnya N, sehingga suatu saat
terdapat kondisi dimana gaya kuat tidak mampu lagi menahan gaya tolak
antar proton. Pada kondisi demikian inti akan mengalami fisi spontan. Pada
umumnya reaksi fisi melibatkan sebuah inti berat dan partikel penembak.
Agar terjadi fisi, energi partikel penembak harus melebihi energi aktivasi.
Energi aktivasi adalah energi yang diperlukan untuk mengakibatkan
terjadinya fisi. Berbeda dengan proses fisi pada umumnya, pada fisi spontan
inti membelah tanpa dipicu partikel penembak. inti dengan sendirinya
(spontan) membelah menjadi dua buah inti baru diikuti oleh pelepasan
sejumlah energi. Pada proses fisi, sebuah inti berat seperti uranium terbelah
menjadi dua inti yang lebih ringan. Karena energi ikat inti ringan adalah
sekitar 1 MeV per nukleon lebih kuat daripada inti berat, maka dalam tiap
proses fisi terjadi pengubahan energi sekitar 200 MeV (200 nukleon x 1
MeV per nukleon). Bandingkan dengan proses-proses elektron dalam yang
hanya melibatkan energi sekitar beberapa elektron volt. Dalam inti terjadi
persaingan antara gaya inti, yang menyatukan inti , dan tolakan elektrostatik
antara berbagai proton dalam inti, yang cenderung memisahkan kesatuan
inti. Bagi sebagian besar inti, gaya inti lah yang menang dalam persaingan
ini ini, tetapi bagi inti-inti berat dan super berat ada perimbangan yang labil
antara gaya inti dan gaya Coulomb, suatu perimbangan yang mudah sekali
tumbang.4 Berdasarkan eksperimen diketahui bahwa energi aktivasi
menurun seiring dengan meningkatnya A. Rumusan massa semi empiris
dapat digunakan untuk menduga kondisi inti yang akan mengalami fisi
spontan. Misalkan sebuah inti
dengan energi ikat per nukleon sebesar
7.54 MeV membelah menjadi dua buah inti dengan A masing-masing 117
dengan energi ikat kira-kira 8.3 MeV. Karena terbelah menjadi dua inti
sedang maka energi ikat inti akhir lebih besar daripada inti awal, maka
sesuai dengan hukum kekekalan energi sejumlah energi harus dilepaskan.
Perubahan energi yang terjadi pada proses ini adalah : energi ikat inti awal
adalah sekitar 234 x 7.54 = -1765 MeV (tanda negatif menujukkan energi
ikat) kemudian setelah mengalami fisi energi total yang dimiliki kedua inti
akhir adalah sekitar 2 x 117 x 8.4 = -1965 MeV. Menurut hukum kekekalan
energi maka keadaan akhir dari inti tersebut harus mengandung kelebihan
energi sebesar kira-kira 200 MeV. Kelebihan energi ini dapat muncul dalam
berbagai bentuk (energi partikel β, energi neutron, atau berupa emisi sinar γ)
tetapi sebagian besar (~80 %) muncul sebagai energi kinetik fragmen kedua
inti akhir 7. Sebelum terjadinya fisi inti akan terlebih dulu mengalami
perubahan bentuk. Menurut model inti tetesan cairan sebuah inti berat dapat
dianalogikan seperti tetesan cairan dengan bentuk kesetimbangan yang agak
sedikit melonjong. Apabila inti tersebut diganggu, seperti menyerap sebuah
neutron atau proton berenergi tinggi, “tetesan” ini bergetar. Bentuk inti
berubah dengan cepat berulang kali dari bentuk yang lebih lonjong ke
bentuk yang agak bundar. Bila inti tertarik ke bentuk yang sangat lonjong,
energi Coulomb tidaklah berubah banyak, tetapi gaya inti melemah, karena
bertambahnya luas permukaan inti (semua nukleon pada permukaan inti
berkurang kekuatan ikatnya). Dengan penarikan yang cukup kuat, bagian
14
tengah tetesan inti menjadi hampir lepas, sehingga inti dengan mudah
terbelah menjadi dua bagian, dan oleh tolakan Coulomb kedua bagian ini
saling terdorong jauh. Di sini perubahan bentuk inti tidak menyebabkan
volume inti berubah. Tetapi perubahan bentuk inti akan menyebabkan luas
permukaan inti bertambah dan karena inti semakin lonjong interaksi
Coulomb menjadi lebih dominan dibanding gaya kuat (karena gaya
Coulomb berjangkauan tak hingga sedangkan gaya kuat berjangkauan
pendek).4 Hasil perhitungan menunjukkan semakin besar nomor massa,
eksentrisitasi inti semakin mendekati 1, artinya inti semakin lonjong.
Menurut perhitungan, eksentrisitas untuk inti-inti berat dan super berat
berkisar 0.75 ~ 0.85. Perubahan energi ikat inti adalah penjumlahan akibat
perubahan koreksi energi Coulomb ditambahan perubahan akibat koreksi
energi permukaan sesuai dengan Persamaan 5. Jika suku kedua lebih besar
dari suku pertama, perubahan energi positif dan diperoleh peningkatan
energi melalui perubahan bentuk inti. Semakin inti lonjong semakin besar
mengalami perubahan bentuk
energi yang diperoleh. Jika sebuah inti
maka akan inti
akan mengalami penambahan energi sebesar 51 MeV.
jadi energi total yang dilepas ketika terjadi fisi adalah perubahan energi
ketika inti mengalami perubahan bentuk (sebelum terjadinya fisi) ditambah
energi yang dilepas ketika inti membelah. Sehingga energi total yang
dilepas jika sebuah inti
membelah menjadi dua inti yang identik adalah
sekitar 250 MeV.
Bila dikaitkan dengan perhitungan probabilitas peluruhan maka
semakin besar energi yang dilepas, maka peluang untuk terjadinya
peluruhan semakin besar. Salah satu faktor yang menghambat terjadinya fisi
Gambar 5. Grafik hubungan jumlah neutron terhadap jumlah proton
15
adalah adanya halangan Coulomb (Coulomb barrier) yang juga menjadi
faktor yang mencegah terjadinya peluruhan α. Jika sebuah inti
menjadi
dua buah inti yang identik yang permukaannya saling bersentuhan maka
halangan Coulombnya adalah sekitar 295 MeV. Jika energi total yang
dilepas lebih besar dari halangan Coulomb maka inti akan mengalami fisi
spontan. Selisih antara halangan Coulomb dan energi total yang terlibat
pada proses fisi adalah energi aktivasi. Gambar 6 memperlihatkan hubungan
antara energi halangan Coulomb dan energi total yang dilepas selama
terjadinya fisi. Berdasarkan perhitungan yang dilakukan pada penelitian ini,
dengan asumsi inti terbelah menjadi dua inti yang identik, diketahui energi
aktivasi naik (dengan mengalami fluktuasi) sampai daerah inti-inti sedang.
Pada daerah inti-inti sedang, energi aktivasi masih mengalami fluktuasi dan
cenderung konstan berkisar 45 sampai 60 MeV, dengan energi aktivasi
terbesar dimiliki oleh inti
MeV. Hal ini masuk akal mengingat inti-inti
sedang memiliki kestabilan yang lebih tinggi, dibanding inti-inti ringan atau
inti-inti berat sehingga untuk membuat inti-inti tersebut fisi dibutuhkan
energi yang besar. Kemudian pada daerah inti-inti berat dan super berat
energi aktivasi cenderung terus menurun, artinya semakin besar nomor
massa sebuah inti semakin mudah untuk membuat inti tersebut untuk
mengalami fisi. Fluktuasi yang terjadi pada energi aktivasi diakibatkan
karena energi ikat inti genap-genap lebih besar daripada inti ganjil-ganjil
atau ganjil-genap maka ketika terjadi fisi (dengan asumsi inti terbelah
menjadi dua inti yang identik), inti genap-genap akan membebaskan energi
lebih besar daripada inti ganjil-ganjil atau ganjil-genap. Hal tersebut akan
menyebabkan energi aktivasi untuk inti genap-genap lebih kecil dibanding
dengan inti ganjil-genap atau ganjil-ganjil. Gambar 6 memperlihatkan
hubungan antara energi total yang dilepas selama terjadinya dan potensial
halangan Coulomb terhadap nomor massa. Kecuali untuk inti helium dan
berilium, sampai dengan nomor massa kira-kira 373 dan nomor atom 135
energi total yang dilepas selalu lebih kecil dari energi halangan Coulomb
(energi aktivasi selalu positif), setelahnya terlihat bahwa energi total yang
dilepas selalu melebihi energi potensial halangan Coulomb (energi aktivasi
negatif) sehingga dapat diduga bahwa inti-inti setelah itu akan mengalami
fisi spontan. Energi aktivasi pada batas tersebut adalah sekitar 0.48 MeV.
Energi aktivasi positif, artinya diperlukan sejumlah energi untuk membelah
inti, sedangkan negatif berarti diperlukkan sejumlah energi untuk
membentuk inti. Berarti dapat diduga inti-inti setelah Z = 135 tidak akan
terbentuk, karena dibutuhkan sejumlah energi untuk membentuk inti-inti
tersebut. Kemudian dari perhitungan diduga bahwa inti akan mengalami fisi
spontan jika rasio Z2/A melebihi 49. Ternyata hasil ini cocok jika
dibandingkan dengan energi aktivasi yang dibutuhkan. Rasio Z2/A pada Z =
135 adalah sekitar 48.86, kemudian Z setelahnya sudah melebihi 49. Dapat
diduga bahwa jika inti diasumsikan terbelah menjadi dua inti yang identik
maka Z = 135 adalah batas dimana inti akan mulai mengalami fisi spontan.
Sehingga kemungkinan terdapat inti-inti super berat yang stabil asalkan
belum melewati batas fisi spontan di atas.
16
Gambar 6. Grafik hubungan energi total yang dilepas ketika fisi dan
halangan Coulomb terhadap nomor massa
Gambar 7. Grafik hubungan energi aktivasi terhadap nomor massa estimasi
17
SIMPULAN DAN SARAN
Simpulan
Model inti tetesan cairan dapat digunakan untuk menghitung dan
menduga isotop paling stabil, energi ikat per nukleon, energi aktivasi, dan
batas terjadinya fisi spontan. Berdasarkan hasil perhitungan yang telah
dilakukan, inti akan mengalami fisi spontan di atas Z = 135. Pada Z = 135
energi yang diperlukan untuk membuat inti mengalami fisi atau energi
aktivasi sangat kecil yaitu sekitar 0.48 MeV. Di atas Z = 135 energi aktivasi
adalah negatif. Kemudian pada Z = 135 rasio Z2/A adalah 48.86, hampir
mencapai syarat rasio Z2/A dimana inti akan mengalami fisi spontan yaitu
49. Energi ikat per nukleon untuk inti-inti super berat sampai Z = 200
adalah sekitar 7 – 5.5 MeV. Walaupun mempunyai energi ikat per nukleon
yang kecil bukan berarti inti-inti akan tidak stabil karena inti-inti ringan
yang stabil seperti litium juga mempunyai energi ikat pada kisaran yang
sama. Dari perhitungan dengan menggunakan model inti tetesan cairan
diduga ada inti super berat sampai nomor atom Z = 135 yang stabil,
sedangkan setelah Z = 135 inti sudah tidak ada lagi inti super berat yang
stabil.
Saran
Untuk penelitian tentang kestabilan selanjutnya, diharapkan kestabilan
inti super berat tidak hanya ditinjau menggunakan satu model saja,
sehingga inti-inti super berat yang diduga stabil bisa ditentukkan secara
lebih spesifik.
18
DAFTAR PUSTAKA
1. Beiser, Arthur. Konsep Fisika Modern. The Houw Liong. Penerjemah :
Carol Manik. Editor. Jakarta : Erlangga. Terjemahan
dari : Concepts
of Modern Physics, 3rd Edition. 1982
2. Gautreau, Ronald, William Savin. Teori dan Soal-soal Fisika Modern.
Penerbit Erlangga. Penerjemah : Soni Astranto, Wibi Hardani, editor.
Jakarta. Terjemahan dari : Schaum`s Outline of Theory and Problems of
Modern Physics Second Edition. 2006
3. Goeppert Maria, J. Hans D. Jensen.. Elementary Theory of Nuclear Shell
Structure. New York : John Wiley and Sons, Inc. 1964
4. Lilley, John. Nuclear Physics : Principles and Applications. New York :
John Wiley and Sons, Inc. 2001
5. N. Subrahmanyan, Brij Lal. Atomic and Nuclear Physics. New Delhi. S.
Chand and Company Ltd. 1996
6. S. Krane, Kenneth. Fisika Modern. Hans J.W. Penerjemah; Sofia
Niksolihin. Editor. Jakarta : UI Press. Terjemahan dari : Modern Physics.
1982
7. S. Krane, Kenneth. Introductory Nuclear Physics. New York. John and
Sons, Inc. 1988
19
LAMPIRAN
Lampiran 1.
Program untuk menduga energi ikat, energi ikat per nukleon,
mencari isotop paling stabil, kondisi terjadinya fisi spontan,
dan energi aktivasi.
clear
clc
av=14;%MeV
as=13;%MeV
ac=0.6;%MeV
aa=19;%MeV
ro=1.25;%fm
k=1.44;%MeV
phi=3.14;
mp=(1.007275).*931.5;%massa proton (MeV)
mn=(1.008665).*931.5;%massa proton (MeV)
dR=0.06;
Z=[ ];%definisi nomor atom
for i=1:200;
Z(i,1)=i
end
%nomor massa yang ada di alam
A1=[1;4;7;9;11;12;14;16;19;20;23;24;27;28;31;32;35;40;39;40;4
5;48;51;52;55;56;59;58;63;64;69;74;75;78;79;84;85;88;89;90;93
;98;98;102;103;106;107;114;115;118;121;128;127;132;133;138;13
9;142;141;144;146;149;154;152;159;156;165;166;169;174;175;180
;181;184;187;192;193;195;197;202;205;208;209;209;210;222;223;
226;227;232;231;238;237;242;243;247;247;251;252;257;258;259;2
60;261;262;271;270;277;278;281;281;285;286;289;289;293;294;29
4;319;322;326;329;332;335;339;342;345;349;352;356;359;362;366
;369;373;376;380;383;386;390;393;397;400;404;407;411;414;418;
422;425;429;432;436;440;443;447;450;454;458;461;465;469;473;4
76;480;484;487;491;495;499;502;506;510;514;518;522;525;529;53
3;537;541;545;549;553;556;560;564;568;572;576;580;584;588;592
;596;600;604;608;612;616;]
%nomor massa estimasi
A2=[1;4;6;8;10;12;14;16;18;20;24;26;28;30;32;34;36;38;40;44;4
6;48;50;52;54;56;60;62;64;66;68;72;74;76;78;80;84;86;88;90;94
;96;98;100;104;106;108;112;114;116;118;122;124;126;129;132;13
4;137;140;142;145;148;151;153;156;159;162;164;167;170;173;176
;178;181;184;187;190;193;196;199;201;204;207;210;213;216;219;
222;225;228;231;234;237;240;243;246;249;252;255;258;262;265;2
68;271;274;277;280;284;287;290;293;296;299;303;306;309;312;31
6;319;322;326;329;332;335;339;342;345;349;352;356;359;362;366
;369;373;376;380;383;386;390;393;397;400;404;407;411;414;418;
422;425;429;432;436;440;443;447;450;454;458;461;465;469;473;4
76;480;484;487;491;495;499;502;506;510;514;518;522;525;529;53
20
3;537;541;545;549;553;556;560;564;568;572;576;580;584;588;592
;596;600;604;608;612;616;]
n=length(A1);
%tanpa koreksi energi pairing dan energi asimetri
for i=1:n;
B(i)=av.*A1(i)-as.*A1(i).^(2./3)-ac.*Z(i).*(Z(i)1)./A1(i).^(1./3);%energi ikat
fb(i)=B(i)./A1(i);%energi ikat per nukleon
N1(i)=A1(i)-Z(i);%jumlah neutron
X1(i)=(Z(i)).^2./A1(i);%Batas fisi spontan
Y1(i)=A1(i)./Z(i);%Rasio nomor massa terhadap nomor atom
R1(i)=N1(i)./Z(i);%Rasio jumlah neutron terhadap jumlah
proton
end
%dengan koreksi energi pairing dan energi asimetri
for i=1:n;
c=rem(A1(i),2);
N1(i)=A1(i)-Z(i);
b=rem(N1(i),2);
a=rem(Z(i),2);
if c==1;
ap(i)=0;
elseif b==1 && a==1;
ap(i)=-34;
else
ap(i)=34;
end
Ev1(i)=av.*A1(i);%energi volume
Es1(i)=as.*(A1(i)).^(2./3);%energi permukaan
Z21(i)=ac.*(Z(i).*(Z(i)-1));
Ax(i)=A1(i).^(1./3);
Ec1(i)=Z21(i)./Ax(i);%energi coulomb
Ea1(i)=aa.*((A1(i)-2.*Z(i)).^2)./A1(i);%energi asimetri
Ep1(i)=ap(i).*A1(i).^(-3./4);%energi pasangan
B1(i)=Ev1(i)-Es1(i)-Ec1(i)-Ea1(i)+Ep1(i);%energi ikat
fb1(i)=B1(i)./A1(i);%energi ikat per nukleon
end
for i=1:n;
B(i)=av.*A1(i)-as.*A1(i).^(2./3)-ac.*Z(i).*(Z(i)1)./A1(i).^(1./3);%energi ikat
fb(i)=B(i)./A1(i);%energi ikat per nukleon
N1(i)=A1(i)-Z(i);%jumlah neutron
X1(i)=(Z(i)).^2./A1(i);%Batas fisi spontan
Y1(i)=A1(i)./Z(i);%Rasio nomor massa terhadap nomor atom
R1(i)=N1(i)./Z(i);%Rasio jumlah neutron terhadap jumlah
proton
end
%dengan koreksi energi pairing dan energi asimetri
for i=1:n;
c=rem(A1(i),2);
N1(i)=A1(i)-Z(i);
b=rem(N1(i),2);
a=rem(Z(i),2);
if c==1;
21
ap(i)=0;
elseif b==1 && a==1;
ap(i)=-34;
else
ap(i)=34;
end
Ev1(i)=av.*A1(i);%energi volume
Es1(i)=as.*(A1(i)).^(2./3);%energi permukaan
Z21(i)=ac.*(Z(i).*(Z(i)-1));
Ax(i)=A1(i).^(1./3);
Ec1(i)=Z21(i)./Ax(i);%energi coulomb
Ea1(i)=aa.*((A1(i)-2.*Z(i)).^2)./A1(i);%energi asimetri
Ep1(i)=ap(i).*A1(i).^(-3./4);%energi pasangan
B1(i)=Ev1(i)-Es1(i)-Ec1(i)-Ea1(i)+Ep1(i);%energi ikat
fb1(i)=B1(i)./A1(i);%energi ikat per nukleon
end
for i=1:n;
c=rem(A2(i),2);
N2(i)=A2(i)-Z(i);
b=rem(N2(i),2);
a=rem(Z(i),2);
if c==1;
ap(i)=0;
elseif b==1 && a==1;
ap(i)=-34;
else
ap(i)=34;
end
Ev2(i)=av.*A2(i);%energi volume
Es2(i)=as.*(A2(i)).^(2./3);%energi permukaan
Z22(i)=ac.*(Z(i).*(Z(i)-1));
Ay(i)=A2(i).^(1./3);
Ec2(i)=Z22(i)./Ay(i);%energi coulomb
Ea2(i)=aa.*((A2(i)-2.*Z(i)).^2)./A2(i);%energi asimetri
Ep2(i)=ap(i).*A2(i).^(-3./4);%energi pasangan
B2(i)=Ev2(i)-Es2(i)-Ec2(i)-Ea2(i)+Ep2(i);%energi ikat
fb2(i)=B2(i)./A2(i);%energi ikat per nukleon
X2(i)=(Z(i)).^2./A2(i);%Batas fisi spontan
Y2(i)=A2(i)./Z(i);%Rasio nomor massa terhadap nomor atom
R2(i)=N2(i)./Z(i);%Rasio jumlah neutron terhadap jumlah
proton
end
%mencari energi aktivasi
for i=1:n;
c=rem(A2(i),2);
N2(i)=A2(i)-Z(i);
b=rem(N2(i),2);
22
a=rem(Z(i),2);
if c==1;
ap(i)=0;
elseif b==1 && a==1;
ap(i)=-34;
else
ap(i)=34;
end
d=rem(A2(i), 2);
%untuk inti dengan nomor massa ganjil
if d==1;
Ao(i)=A2(i)./2;
Ar(i)=Ao(i)+0.5;
As(i)=Ao(i)-0.5;
betar(i)=mp-mn-(ac./(Ar(i).^(1/3)))-aa.*4;
gammar(i)=(ac./Ar(i).^(1/3))+((aa.*4)./Ar(i));
Zr(i)=-(betar(i)./(2.*gammar(i)));
betas(i)=mp-mn-(ac./(As(i).^(1/3)))-aa.*4;
gammas(i)=(ac./As(i).^(1/3))+((aa.*4)./As(i));
Zs(i)=-(betas(i)./(2.*gammas(i)));
R1(i)=(ro.*(Ar(i)).^(1./3))+(ro.*(As(i)).^(1./3));
Cb(i)=k.*(((Zr(i).*Zs(i)))./(R1(i)));%Coulomb
Barrier
Evr(i)=av.*Ar(i);%energi volume
Esr(i)=as.*(Ar(i)).^(2./3);%energi permukaan
Z2r(i)=ac.*(Zr(i).*(Zr(i)-1));
Ayr(i)=Ar(i).^(1./3);
Ecr(i)=Z2r(i)./Ayr(i);%energi coulomb
Ear(i)=aa.*((Ar(i)-2.*Zr(i)).^2)./Ar(i);%energi
asimetri
Epr(i)=ap(i).*Ar(i).^(-3./4);%energi pasangan
Br(i)=Evr(i)-Esr(i)-Ecr(i)-Ear(i)+Epr(i);%energi ikat
fbr(i)=Br(i)./Ar(i);%energi ikat per nukleon
Eer(i)=Ar(i).*fbr(i);%energi ikat setelah fisi
Evs(i)=av.*As(i);%energi volume
Ess(i)=as.*(As(i)).^(2./3);%energi permukaan
Z2s(i)=ac.*(Zs(i).*(Zs(i)-1));
Ays(i)=As(i).^(1./3);
Ecs(i)=Z2s(i)./Ays(i);%energi coulomb
Eas(i)=aa.*((As(i)-2.*Zs(i)).^2)./As(i);%energi
asimetri
Eps(i)=ap(i).*As(i).^(-3./4);%energi pasangan
Bs(i)=Evs(i)-Ess(i)-Ecs(i)-Eas(i)+Eps(i);%energi ikat
fbs(i)=Bs(i)./As(i);%energi ikat per nukleon
Ees(i)=As(i).*fbs(i);
Ee(i)=Ees(i)+Eer(i);%energi ikat setelah fisi
E_re(i)=Ee(i)-B2(i);%energi yang dilepas
E_act(i)=Cb(i)-E_re(i);
23
else
%untuk inti dengan nomor massa genap
At(i)=A2(i)./2;
beta(i)=mp-mn-(ac./(At(i).^(1./3)))-aa.*4;
gamma(i)=(ac./At(i).^(1./3))+((aa.*4)./At(i));
Zt(i)=-(beta(i)./(2.*gamma(i)));
R1(i)=ro.*(At(i)).^(1./3);
Cb(i)=k.*((Zt(i)).^2)./(2.*(R1(i)));%Coulomb Barrier
Evt(i)=av.*At(i);%energi volume
Est(i)=as.*(At(i)).^(2./3);%energi permukaan
Z2t(i)=ac.*(Zt(i).*(Zt(i)-1));
Ayt(i)=At(i).^(1./3);
Ect(i)=Z2t(i)./Ayt(i);%energi coulomb
Eat(i)=aa.*((At(i)-2.*Zt(i)).^2)./At(i);%energi
asimetri
Ept(i)=ap(i).*At(i).^(-3./4);%energi pasangan
Bt(i)=Evt(i)-Est(i)-Ect(i)-Eat(i)+Ept(i);%energi ikat
Ee(i)=2.*Bt(i);%energi ikat setelah fisi
E_re(i)=Ee(i)-B2(i);%energi yang dilepas
end
end
for i=1:n;
Dp(i)=(4./3).*(3.14./5).^(1/2).*(dR./ro.*(A2(i)).^(1./3));%pa
rameter deformasi
ecc(i)=Dp(i).*(5./4.*phi).^(1/2);%eksentrisitas
%perubahan energi ikat akibat deformasi
Esurf(i)=((2./5).*as.*(A2(i)).^(2./3)).*(ecc(i)).^2;
Ecoul(i)=((1./5).*ac.*(Z(i)).^2).*(A2(i)).^(1./3).*(ecc(i)).^2;
dE(i)=(((2./5).*as.*(A2(i)).^(2./3)+(1./5).*ac.*(Z(i)).^2).*(A2(i)).^
(-1./3)).*(ecc(i)).^2;
dddE(i)=dE(i)+E_re(i)%energi total yang dilepas ketika
inti mengalami fisi
ddE(i)=Cb(i)-dddE(i);%energi aktivasi
end
%menghitung jumlah inti genap-genap, genap-ganjil, ganjilganjil, dan
%ganjil-genap untuk nomor massa yang nyata
for i=1:n;
EE(i)=0;
EO(i)=0;
OO(i)=0;
OE(i)=0;
w=rem(N1(i), 2)
24
f=rem(Z(i), 2)
if w==0 && f==0;
EE1(i+1)=EE(i)+1;
g=sum(EE1);
elseif w==0 && f==1;
EO1(i+1)=EO(i)+1;
h=sum(EO1);
elseif w==1 && f==1;
OO1(i+1)=OO(i)+1;
j=sum(OO1);
else
OE1(i+1)=OE(i)+1;
m=sum(OE1);
end
end
%menghitung jumlah inti genap-genap, genap-ganjil, ganjilganjil, dan
%ganjil-genap untuk nomor massa estimasi
for i=1:n;
EE11(i)=0;
EO11(i)=0;
OO11(i)=0;
OE11(i)=0;
u=rem(N2(i), 2)
y=rem(Z(i), 2)
if u==0 && y==0;
EE3(i+1)=EE11(i)+1;
g2=sum(EE3);
elseif u==0 && y==1;
EO3(i+1)=EO11(i)+1;
h2=sum(EO3);
elseif u==1 && y==1;
OO3(i+1)=OO11(i)+1;
j2=sum(OO3);
else
OE3(i+1)=OE11(i)+1;
m2=sum(OE3);
end
end
%plot(A1, fb1, 'red', A2, fb2, 'blue')
%plot(A1, fb2)
%plot(A2, fb2, A1, fb1)
%plot(Z, ddE)
%plot(Z, X2)
plot(A2, Esurf, A2, Ecoul)
xlabel('Nomor Massa'), ylabel('Energi (MeV)')
grid on
25
legend('Energi permukaan', 'Energi potensial Coulomb')
%subplot(1,2,1)
%plot(A1, fb, A1, fb1)
%xlabel('nomor massa (A)'), ylabel('energi ikat per nukleon
(fb)')
%subplot(1,2,2)
%plot(Z, A1)
%xlabel('Z'), ylabel('A')
disp(' Z A (Eks) N(Eks) fb(Eks)
A(Est) N(Est)
fb(Est) ')
disp('-------------------------------------------------------------------')
for i=1:length(Z)
string = '%2.0f
%2.0f
%2.0f
%6.04f
%6.0f
%2.0f
%6.04f' ;
disp(sprintf(string,i,A1(i), N1(i), fb1(i), A2(i), N2(i),
fb2(i)))
end
disp('--------------------')
disp('-------------------------------------------------------------------')
for i=1:length(Z)
string = '%2.0f
%2.0f
%2.0f
%2.02f
%2.02f
%2.02f
%2.02f
%2.02f' ;
disp(sprintf(string, A2(i), Z(i), N2(i), Cb(i), dddE(i),
dE(i)))
end
disp('--------------------')
26
RIWAYAT HIDUP
Penulis dilahirkan di Cianjur pada tanggal 10 Mei
1991 dari Ayah Anang Pirtana dan Ibu Ema
Setiawati. Penulis adalah putra pertama dari empat
bersaudara. Tahun 2009 penulis lulus dari SMA
Negeri 1 Sukanagara dan pada tahun yang sama
penulis lulus seleksi masuk Institut Pertanian
Bogor (IPB) melalui jalur Undangan Seleksi
Masuk IPB dan diterima di Departemen Fisika, Fakultas Matematika dan
Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten praktikum
Fisika TPB pada tahun ajaran 2010/2011, 2011/2012 dan 2012/2013, asisten
praktikum Fisika Modern pada tahun ajaran 2011/2012 dan 2012/2013,
asisten praktikum Sensor dan Transduser pada tahun ajaran 2012/2013, dan
asisten praktikum Fisika Dasar 2 pada tahun ajaran 2012/2013. Penulis juga
aktif mengajar mata kuliah Fisika TPB dan Fisika Dasar 2 di bimbingan
belajar dan privat mahasiswa Katalis Corporation. Penulis juga pernah aktif
sebagai staf Pengembangan Sumber Daya Manusia Himpunan Mahasiswa
Fisika IPB.
.
27
28