KUTUB EMPAT

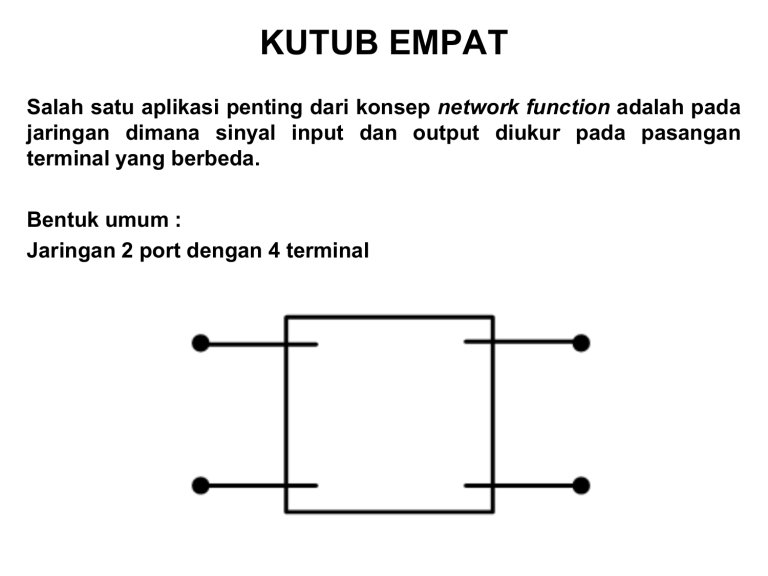
KUTUB EMPAT
Salah satu aplikasi penting dari konsep network function adalah pada
jaringan dimana sinyal input dan output diukur pada pasangan
terminal yang berbeda.
Bentuk umum :
Jaringan 2 port dengan 4 terminal
• Adapun teori rangkaian (K-4) ini banyak dipergunakan
pada jaringan yang dipergunakan dalam sistem
komunikasi, sistem daya, sistem kontrol dan rangkaian
elektronik (model transistor).
• Pada rangkaian (K-4) ini banyak memerlukan hubungan
antara V1, V2, I1, dan I2 yang salingindependent, dimana
berbagai macam hubungan antara tegangan dan arus
disebut sebagai parameter.
Jaringan 2 port dengan 3 terminal
1.
2.
3.
4.
Parameter Z
Parameter Y
Parameter hybrid
Paramater ABCD
Parameter Z
Misalkan : I1 dan I2 adalah input
V1 dan V2 adalah output
Maka :
V1  Z11 I 1  Z12 I 2
V2  Z 21 I 1  Z 22 I 2
Parameter Z (cont.)
Jika port 2 open circuit (I2 = 0), sehingga :
V1
Z 11 
I1
Z 21
V2

I1
I 2 0
I 2 0
Jika port 1 open circuit (I1 = 0), sehingga :
Z 21
Z 22
V1

I2
I1  0
V2

I2
I1  0
Parameter Z (cont.)
Impedansi yang dihasilkan sebagai impedansi open circuit atau
parameter open circuit atau parameter Z.
Z11
= impedansi port primer ketika port sekunder open circuit
Z22
= impedansi port sekunder ketika port primer open circuit
Z12 = Z21 = impedansi transfer dimana perbandingan tegangan disatu
port dibandingkan arus di port lainnya.
Contoh soal :
Tentukan parameter Z !
Parameter Y
Misalkan : V1 dan V2 adalah input
I1 dan I2 adalah output
Maka :
I 1  Y11V1  Y12V2
I 2  Y21V1  Y22V2
Parameter Y (cont.)
Jika port 2 short circuit (V2 = 0), sehingga :
I1
Y11 
V1
V2  0
I2
Y21 
V1
V2  0
Jika port 1 short circuit (V1 = 0), sehingga :
I1
Y21 
V2
V1  0
I2
Y22 
V2
V1  0
Parameter Y (cont.)
Admitansi yang dihasilkan sebagai admitansi short circuit atau
parameter short circuit atau parameter Y.
Contoh soal :
Tentukan parameter Y dalam domain j !
Parameter Hybrid
Parameter hybrid h
Misalkan : I1 dan V2 adalah input
V1 dan I2 adalah output
Maka :
V1  h11 I 1  h12V2
I 2  h21 I 1  h22V2
Parameter Hybrid h (cont.)
Jika port 2 short circuit (V2 = 0), sehingga :
V1
h11 
I1
V2  0
I2
h21 
I1
V2  0
Jika port 1 open circuit (I1 = 0), sehingga :
V1
h12 
V2
I1  0
I2
h22 
V2
I1  0
Parameter hybrid g
Misalkan : V1 dan I2 adalah input
I1 dan V2 adalah output
Maka :
I 1  g11V1  g12 I 2
V2  g 21V1  g 22 I 2
Jika port 2 open circuit (I2 = 0), sehingga :
I1
g 11 
V1
g 21
V2

V1
I 2 0
I 2 0
Parameter hybrid g (cont.)
Jika port 1 short circuit (V1 = 0), sehingga :
g 12
g 22
I1

I2
V1  0
V2

I2
V1  0
Parameter ABCD
Parameter ini penting untuk engineering transmisi sebab disisi primer
(pengirim) terdiri dari variable V1 dan I1, sedangkan disisi
sekunder (penerima) terdiri dari variabel V2 dan - I2 (negatif I2
karena arus masuk ke beban penerima).
• Kutub 4 juga dapat dinyatakan tanpa menggunakan
impedansi atau admintasi, yakni hanya menggunakan
variabel tegangan dan arus yaitu parameter transmisi
(ABCD)
• V1= A V2 . B V2
• I1 = C V2 . D V2
• Parameter ini penting untuk teknik transmisi, sebab disisi
primer (pengirim) terdiri dari variabel V1 dan I1,
sedangkan (penerima) terdiri dari variabel V2 dan
I2 (negatif I2 karena arus masuk ke beban penerima)
Parameter ABCD (cont.)
Misalkan : V2 dan I2 adalah input
V1 dan I1 adalah output
Maka :
V1  AV2  BI 2
I 1  AV2  BI 2
Jika port 2 open circuit (I2 = 0), sehingga :
V1
A
V2
I 2 0
I1
C
V2
I 2 0
Parameter ABCD (cont.)
Jika port 2 short circuit (V2 = 0), sehingga :
V1
B
 I2
I1
D
 V2
V2  0
V2  0
Interkoneksi Kutub Empat
Koneksi Paralel
Koneksi Paralel (cont.)
I 1a  Y11aV1a  Y12aV2 a
I 2 a  Y21aV1a  Y22aV2 a
I 1b  Y11bV1b  Y12bV2b
I 2b  Y21bV1b  Y22bV2b
Dimana :
V1  V1a  V1b
V2  V2 a  V2 b
I 1  I 1a  I 1b
I 2  I 2 a  I 2b
Koneksi Paralel (cont.)
I 1  I 1a  I 1b
I 1  Y11aV1a  Y12aV2 a  Y11bV1b  Y12bV2b
I 1  (Y11a  Y11b )V1  (Y12a  Y12b )V2
I 2  I 2 a  I 2b
I 2  Y21aV1a  Y22aV2 a  Y21bV1b  Y22bV2b
I 2  (Y21a  Y21b )V1  (Y22a  Y22b )V2
dengan demikian :
Y11  Y11a  Y11b
Y12  Y12a  Y12b
Y21  Y21a  Y21b
Y22  Y22a  Y22b
Koneksi Seri
Koneksi Seri (cont.)
V1a  Z 11a I 1a  Z 12a I 2 a
V2 a  Z 21a I 1a  Z 22a I 2 a
V1b  Z 11b I 1b  Z 12b I 2b
V2b  Z 21b I 1b  Z 22b I 2b
Dimana :
I 1  I 1a  I 1b
I 2  I 2 a  I 2b
Koneksi Seri (cont.)
V1  V1a  V1b  Z11a I 1a  Z12a I 2 a  Z11b I 1b  Z 12b I 2b  Z 11a I 1a  Z11b I 1b  Z12a I 2 a  Z12b I 2b
V1  ( Z11a  Z11b ) I 1  ( Z12a  Z12b ) I 2
V2  V2 a  V2b  Z 21a I 1a  Z 22a I 2 a  Z 21b I 1b  Z 22b I 2b  Z 21a I 1a  Z 21b I 1b  Z 22a I 2 a  Z 22b I 2b
V2  ( Z 21a  Z 21b ) I 1  ( Z 22a  Z 22b ) I 2
dengan demikian :
Z11  Z11a  Z11b
Z12  Z12a  Z12b
Z 21  Z 21a  Z 21b
Z 22  Z 22a  Z 22b
Koneksi Kaskade
V1  V1a  AaV2 a  Ba I 2 a  AaV1b  Ba I 1b  Aa ( AbV2b  Bb I 2b )  Ba (CbV2b  Db I 2b )
V1  ( Aa Ab  Ba Cb )V2b  ( Aa Bb  Ba Db ) I 2b
I 1  (C a Ab  Da Cb )V2  (C a Bb  Da Db ) I 2
Dimana :
A  Aa Ab  Ba C b
B  Aa Bb  Ba Db
C  C a Ab  Da C b
D  C a Bb  Da Db
Tabel konversi kutub 4
Rencana pertemuan
selanjutnya
• 27 Desember 2013 pukul 8.40-11.00
presentasi ruang menyusul
• 3 januari 2014 pukul 8.40 – selesai quiz
materi UAS B.41
• Sifat UAS open 1 note A4, calculator