Gerbang logika

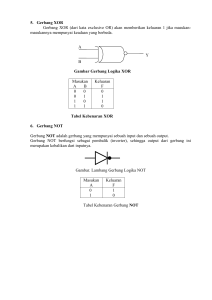
Gerbang Logika
1.
2.
3.
4.
5.
6.
Dwi Indra Oktoviandy
Faiz Hammam
Delva Rizal
Bajeng Nurul W.
Zhafira Amajida
Eggie Addenda C.
(A11.2012.07105)
(A11.2012.07111)
(A11.2012.07108)
(A11.2012.06986)
(A11.2012.06981)
(A11.2012.07301)
Pengertian
• Gerbang logika (logic gate) merupakan
diagram block simbol rangkainan digital
yang memproses sinyal masukan menjadi
sinyal keluaran dengan perilaku tertentu.
Tipe dasar dan turunan gerbang
logika
• AND
• OR
• NOT
Masing masing gerbang dasar ini dapat
dikombinasikan
• NAND(NOT AND)
• NOR (NOT OR)
• XOR (EXLCLUSIVE OR)
• XNOR (EXCLUSIVE NOT OR)
Logika ALjabar
• Aljabar bolean bekerja berasarkan prinip
true dan false yg bisa dinyatakan dengan
nilai 1 untuk true dan 0 untuk false.
Aturan aljabar boolean
•
•
•
•
•
•
•
•
Operasi AND
Operasi OR
Operasi NOT
Hukum Asosiatif
Hukum Distributif
Hukum Komunikatif
Aturan Prioritas
Teorema DeMorgan
(.)
(+)
(‘)
(Associative Law)
(Distributive Law)
(Commutative Law)
(Precedence)
Operasi AND
•
•
•
•
0.0=0
1.0=0
0.1=0
1.1=1
•
•
•
•
A.0=0
A.1=A
A.A=A
A . A’ = 0
Operasi OR
•
•
•
•
0+0=0
1+0=1
0+1=1
1+1=1
•
•
•
•
A+0=A
A+1=1
A+A=A
A + A’ = 1
Operasi NOT
• 0’ = 1
• 1’ = 0
• A” = A
Hukum Asosiatif (Associative Law)
• (A.B).C = A.(B.C) = A.B.C
• (A+B)+C = A+(B+C) = A+B+C
Hukum Distributif (Distributive Law)
• A.(B+C) = (A.B) + (A.C)
• A+(B.C) = (A.B) + (A.C)
Hukum Komunikatif (Commutative Law)
• A.B = B.A
• A+B = B+A
Teorema Prioritas (Procedence)
• AB = A.B
• A.B+C = (A.B)+C
• A+B.C = A.(B+C)
Teorema DeMorgan
• (A.B)’ = A’+B’
• (A+B)’ = A’.B’
(NAND)
(NOR)
Macam-macam Gerbang Logika
• Gerbang Dasar
a. AND
b. OR
c. NOT
• Gerbang Turunan
a. NAND (NOT AND)
b. NOR (NOT OR)
c. XOR (EXCLUSIVE OR)
d. XNOR
AND
Gerbang AND adalah rangkaian elektronik
yang mengeluarkan nilai 1 jika semua
inputnya bernilai 1. Operasi AND
menggunakan tanda (.), seperti : C = A.B =
A AND B.
OR
Gerbang OR adalah rangkaian elektronik
yang mengeluarkan nilai 1 jika salah satu
input-nya bernilai 1. Tanda (+) menunjukkan
operasi OR. Contoh C = A+B = A OR B.
NOT
Gerbang NOT adalah rangkaian yang
mempunyai output berkebalikan dari nilai
input. Simbol operasi NOT adalah “NOT”, “ ‘
“, atau “ ⁻ “. Ā = A’ = NOT A.
NAND (NOT AND)
Gerbang NAND adalah gabungan antara
gerbang AND dan NOT, atau kebalikan dari
gerbang AND. Keluaran gerbang NAND
akan 1 jika salah satu masukannya bernilai
0. Contoh : C = A.B = A NAND B.
NOR
Gerbang NOR adalah gabungan gerbang
OR diikuti gerbang NOT, atau merupakan
kebalikan gerbang OR. Keluaran gerbang
NOR adalah 0 jika input-nya 1.
XOR (EXCLUSIVE OR)
Gerbang XOR adalah rangkaian elektronik
yang akan bernilai 1 jika masukannya
berbeda. Simbol dari operasi XOR adalah .
XNOR
Gerbang XNOR adalah rangkaian elektronik
yang mengeluarkan nilai 1 jika input-nya
sama. Gerbang XNOR merupakan
gabungan antara gerbang XOR dan NOT.
Kombinasi Gerbang Logika
Gerbang logika dapat dikombinasikan satu
dengan yang lainnya untuk mendapatkan
fungsi baru. Contohnya adalah kombinasi
antara gerbang NOT dengan AND seperti
gambar berikut :
Q = A AND (NOT B)
Selain kombinasi 2 gerbang, juga ada kombinasi 3 gerbang
logika seperti gambar berikut :
Rangkaian di atas merupakan kombinasi antara gerbang
NOR, AND, dan OR. Dapat dinyatakan bahwa :
D = A NOR B
E = B AND C
Q = D NOR E = (A NOR B) NOR (B AND C)
• Tabel Kebenaran kombinasi 3 gerbang
pada slide sebelumnya adalah :
MASUKAN
KELUARAN
A
B
C
D = A NOR B
E = B AND C
Q = D NOR E
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
1
1
1
0
Gerbang Logika dalam Chip
Gerbang logika dibuat pabrik dalam chipset.
Biasanya dalam satu chip terdiri dari
beberapa buah gerbang logika.
Chip 7400, mengandung
empat gerbang NAND dengan
tambahan jalur satu daya
(+5V) dan satu ground.
Materi Tambahan
Organisasi Komputer
Edisi 5
Carl Hamacher
Zvonko Vranesic
Safwat Zaky
Sintesis Fungsi Logika
• Misalkan suatu table terdiri dari dua
gerbang AND dan satu gerbang Or.
Jaringan tersebut dapat dinyatakan
dengan ekspresi
Ƒ= x1 .x 2 + x1.x2
• Ekspresi tersebut disebut juga sumproduct karena operasi OR sering disebut
fungsi “sum” dan operasi AND fungsi
“product”
Sintesis Fungsi Logika
• Kita
sebaiknyamemperhatikanbahwaakanlebihsesuaiu
ntukmenuliskan
f = ((𝑥1 ) . 𝑥2 + (𝑥1 . (𝑥2 ))
• Untukmengindikasikanurutanpenerapanoperasidal
amekspresitersebut.
Untukmenyederhanakantempilanekspresitersebut,
kitadefinisikanhierakiantara AND ,OR , NOT.
Tanpatandakurung ,
operasidalamekspresilogikasebaiknyadilakukande
nganurutan NOT, AND,
kemudianOR.selanjutntalazimmenghilangkan
operator “ . “ padasaattidakadaambiguitas.
Minimalisasi ekspresi logika
• Untukmenyederhanakanekspresilogikakita
akanmelakukansuaturangkaianmanipulasi
aljabar. Aturanlogikabaru yang
akankitamanipulasiadalahaturan
distributive.
w (y+z) = wy + wz
Dan identitas
w + 𝑤2 = 1
Minimalisasi ekspresi logika
• Tujuan dalam memanipulasi logika adalah untuk mengurangi biaya
implementasi fungsi logika tertentu menurut beberapa kriteria.
• Strategi umum dalam melakukan manipulasi aljabar adalah sebagai
berikut.
• Pertama,pasangan product term kelompok yg berbeda hanya pada
beberapa variable yang complemented(x) pada satu term dan true
(x) dalam term lain. Pada saat subproduct gabungan yang terdiri
dari variable lain difaktorkan berdasarkan pasangannya dengan
aturan distributive,kita mendapatkan term x+(x) , yg bernilai 1.
menerapkan prosedur ini ke ekspresi untuk ƒ1 , kita mendapatkan)
Minimalisasi menggunakan peta
karnaugh
• Peta karnaugh adalah teknik geometric yg dapat
digunakan untuk secara cepat mendapatkan
ekspresi minimal untuk fungsi logika beberapa
variable. Teknik tersebut tergantung pada
bentuk ekspresi table kebenaran yang berbedabeda.
SINTESIS DENGAN GERBANG
NAND DAN NOR
Gerbang NAND dan NOR
mengimplementasikan kesetaraan fungsi
AND dan OR diikuti dengan fungsi NOT.
Jika misalkan panah “↑” dan “↓” masingmasing menyatakan operator NAND dan
NOR, dan menggunakan aturan de Morgan
maka kita mendapatkan
x1  x2  x1 x2  x1  x2
Dan
x1  x2  x1  x2  x1 x2
Tersedia gerbang NAND dan NOR dengan lebih
dari dua variabel input, dan keduanya beroperasi
sesuai dengan generalisasi yang jelas dari hukum
de Morgan sebagai
x1  x2  ...  xn  x1 x2 ...xn  x1  x2  ...  xn
dan
x1  x2  ...  xn  x1  x2  ...  xn  x1 x2 ...xn
Perhatikan manipulasi aljabar suatu
ekspresi logika berikutyang dihubungkan ke
jaringan empat-input yang terdiri dari tiga
gerbang 2-input NAND :
Gambar gerbang logika dari manipulasi
aljabar pada slide sebelumnya :
Cascading Gerbang AND dan
OR
Fungsi tiga-input AND dan OR dengan
cascade 2 gerbang dua-input AND dan OR.
Cascading Gerbang NAND
Fungsi tiga-input NAND tidak dapat
diimplementasikan dengan cascade 2 gerbang
dia-input NAND seperti gerbang AND atau OR.
Namun diperlukan tiga gerbang, seperti yang
ditunjukkan gambar berikut :
Terima Kasih