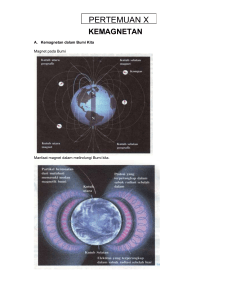
Gaya magnet pada penghantar berarus

Matakuliah
Tahun
Versi
: D0564/Fisika Dasar
: September 2005
: 1/1
Pertemuan 18 - 19
Medan Magnet, Gaya Magnet dan
Gaya Gerak Listrik Induksi
1
Learning Outcomes
Pada akhir pertemuan ini, diharapkan mahasiswa
akan mampu :
• Menjelaskan konsep medan magnet, gaya magnet
dan gaya gerak listrik induksi (C2)
2
Outline Materi
• Medan magnet dan kuat medan magnet, hukum
Biol-savart
• Gaya magnet, gaya Lorenz
• Gaya gerak listrik (ggl) induksi, hukum LenzFaraday
3
MEDAN MAGNET
Muatan listrik selalu mengeluarkan medan listrik.
Muatan listrik yang bergerak mengeluarkan medan
listrik dan Medan Magnet.
Arus listrik merupakan gerakan elektron, sehingga
akan membangkitkan medan magnet disekitar
kawat penghantarnya.
Simbul-simbul besaran dalam medan magenet:
 = fluks magnet, merupakan jumlah garis gaya
magnet. (satuan WEBER, W)
4
B = rapat medan magnet, merupakan fluks
magnet persatuan luas bidang yang
ditembus. (satuan W/m2)
H = Intensitas medan magnet atau kuat medan
magnet. (satuan : Ampere/meter, A/m)
B = oH
(18.1)
o = permeabilitas hampa (satuan W/Am)
= 4 x 10-7 W/Am
 = permeabilitas medium
r = permeabilitas relatif = /o
5
Hubungan antara B dan  dinyatakan:
 = A.B
= A B cos 
dimana A : luasan loop yang ditembus
(18.2)
6
Fluks magnet didefinisikan sebagai banyaknya
garis gaya magnet yang menembus tegak lurus
luasan, dan ditulis:
 =  B dA
(18.3)
Fluks magnet dapat ditingkatkan dengan cara
memberikan bahan feromegnetik di dalam luasan
tersebut. (ingat =r o)
7
HUKUM BIOT SAVART
Hukum Biot-Savart menjelaskan besar dan arah
medan magnet di sekitar kawat berarus.
1. Kawat lurus berarus.
Medan magnet B pada titik p yang berjarak a
dari kawat yang panjangnya l dan dialiri arus
I dinyatakan sbb:
p
a
1
i
l
2
8
o i
cos 1  cos  2 
Bp 
4a
(18.4)
Jika panjang kawat tak berhingga (∞), maka:
o i
Bp 
2a
(18.5)
Jika posisi p simetri tengah:
o i
cos 1 
Bp 
2a
(18.6)
9
2.Kawat lingkaran berarus.
r
i
p
Bp 
o i
(18.7)
2r
3.Kawat kumparan (solenoida)
l
2
1
N
i
R
l
10
Bp 
o Ni
2l
sin 2  sin1 
(18.8)
jika l>>R, maka bedan B di pusat solenoida:
Bp 
o Ni
(18.9)
l
4.Kumparan Toroida (kumparan lingkaran).
i
Rd
N
Rl
11
Medan magnet di dalam kumparan (posisi
Rd<r<Rl):
oNi
B 
2r
(18.10)
Medan magnet pada r<Rd dan r>Rl sama dengan
nol.
GAYA MAGNETIK
• Gaya magnetik pada partikel bermuatan
12
Partikel bermuatan Q coulomb bergerak dengan
kecepatan pada suatu medan magnet , akan
mengalami gaya :
F = qV  B  q V B sin r̂
  sudut antara V dan B
Jika V sejajar B, maka gaya F  0
Gaya magnet pada penghantar berarus :
Jika kawat sepanjang l dialiri arus i dan berada
dalam medan B, maka :
13
I = dQ
dt
 dQ = I dt

 
dF = dQ V  B
 
= I dt V  B


= I  V dt  B


= I d  B

Untuk penghantar yang lurus dan B
yang konstan, maka :
F = I L B sin 
14
dengan :
 = sudut antara L dan B
HUKUM FARADAY
Jika fluks magnet yang menembus loop tertutup
berubah terhadap waktu, maka terjadi gaya gerak
listrik (ggl) induksi () pada loop tersebut.
d
d
   N   N ( AB cos )
dt
dt
(18.11)
N = jumlah lilitan pada loop
15
Perubahan fluks magnet dapat dikarenakan:
•Perubahan karena fungsi sinusoidal arus bolak-balik
•Fungsi putaran ().
Kesimpulan:
Ggl induksi akan timbul pada loop tertutup jika ada
perubahan terhadap waktu (minimum salah satu)
dari A, B atau .
16
INDUKTANSI
1. Induktasi bersama.
Jika batang besi yang panjangnya l dililit dengan
kumparan sehingga jumlah lilitannya N1
kemudian dialiri arus i1, maka akan timbul
medan magnet.
B
 o N1i1
l1
17
Jika kemudian di luar lilitan pertama dililitkan lagi
kawat lain dengan jumlah lilitan N2, maka ggl
induksi akan terjadi pada lilitan kedua, yaitu:
di1
 21   M 21
dt
(18.12)
M21disebut Induktasi bersama, yang nilainya:
M 21 
 o N1 N 2 A
(18.13)
l
Hal yang sama akan terjadi jika yang diberi arus
pada lilitan dua, dimana M21 = M12
18
2.Induktansi Diri
l
i
N
Jika kumparan dialiri arus yang berubah sebagai
fungsi waktu, maka akan terjadi induksi diri
sehingga timbul ggl pada kumparan itu sendiri.
19
d
 di
di
  N
 N
 L
dt
i dt
dt
(18.14)
N o N A
L

i
l
(18.15)
2
Jika dalam kumparan ada inti besi, dengan
=ro maka induktansi dan ggl induksinya juga
berubah dengan faktor r
Contoh.
20
1. Suatu kawat yang panjangnya 5 m dialiri arus
20 A.
a. Jika kawat dibentuk persegi, tentukan kuat
medan di pusat diagonalnya?
b. Juka kawar dibuat lingkaran, tentukan kuat
medan magnet di pusatnya?
Jawab:
21
a. Jika kawat berbentuk persegi empat, maka
panjang sisinya :5/4 = 1,25 m.
Jarak terdekat dari kawat ke pusat diagonal
adalah: a = 1,25/2 = 0,625 m
Dari pers. 16.6 diperoleh kuat medan di pusat
adalah:
B
i
1
i 2
H
 4x

 14,4 A / m
o
2a 2 a
22
b. Kawat berbentuk lingkaran, keliling 5 m.
Jari-jarinya: 0,796 m
Kuat medan di pusat diperoleh dari pers. 16.7,
yaitu: H= i/2r = 12,6 A/m
23
24