listrik statis

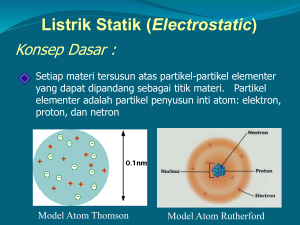
LISTRIK STATIS
Benda menurut muatannya terbagi menjadi :
1. Benda netral :
Benda yang tidak bermuatan / jumlah muatan positif dan negatif sama besarnya.
2. Benda bermuatan listrik :
a. Benda bermuatan listrik positif ( + )
b. Benda bermuatan listrik negatif ( - )
Secara atomik setiap benda terdiri dari muatan positif dan negatif yang dalam keadaan netral jumlahnya
sama. Di dalam atom tersebut juga terdapat netron.
Lalu bagaimanakah suatu benda dapat menjadi bermuatan ?
Lakukan kegiatan berikut :
1. Gosokkan sisir plastik dengan kain wol, kemudian dekatkan potongan kertas kecil kecil pada
sisir plastik tersebut.
Sisir plastik menjadi bermuatan negatif. Ini dikarenakan elektron dari kain wol yang berpindah
ke sisir sehingga kelebihan elektron. Sementara kain wol menjadi bermuatan positif, karena
kekurangan elektron.
2. Gosokkan batang kaca dengan kain sutera, kemudian untuk mengujinya dekatkan potongan
kertas kecil kecil pada batang kaca.
Batang kaca akan menjadi bermuatan positif karena elektron-elektronnya sebagian berpindah ke
kain sutera, dan kain sutera menjadi bermuatan negatif karena kelebihan elektron.
Kesimpulan :
Suatu benda dapat menjadi bermuatan karena benda tersebut menerima/melepaskan elektron.
Benda menjadi bermuatan (+) karena kekurangan elektron (melepaskan elektronnya)
Benda menjadi bermuatan negatif karena menerima tambahan elektron dari benda lain.
Secara umum jumlah muatan listrik adalah kekal.
Disekitar benda bermuatan terdapat medan listrik yaitu ruangan disekitar muatan listrik yang mana jika
ada muatan disekitarnya pengaruh gaya listrik oleh muatan itu masih dapat terpengaruh.
Medan listrik dinyatakan dengan garis gaya listrik yaitu garis khayal yang menyatakan kekuatan gaya
listrik di sekitar muatan listrik.
Arah Garis gaya menunjukkan arah medan listrik, dimana :
Untuk muatan positif ( + ) :
Untuk muatan negatif ( - ) –
–
+
Sifat muatan listrik :
a. Muatan sejenis akan tolak menolak :
+
+
–
–
+
–
b. Muatan berlawanan saling tarik menarik :
A. GAYA COULOMB :
Gaya Interaksi antara dua muatan besarnya sebanding dengan hasil kali antara besar muatan masing
masing dan berbanding terbalik dengan kuadrat jarak antara dua muatan.
Gaya yang terbentuk disebut dengan Gaya Coulomb, dirumuskan :
F  k.
q1.q 2
R2
q1 dan q2 = besarnya muatan masing masing ( tak
perlu dimasukkan tanda (+) atau (-) nya ( C )
R = jarak antara kedua muatan ( m )
F = Gaya coulomb ( N )
k = konstanta pembanding ( N.m2 /c2 )
Catatan :
Arah Gaya Coulomb ditentukan berdasarkan interaksi dua muatan dari Positif ( + ) ke
negatif ( - ).
Jenis muatan menentukan jenis interaksi, yaitu tolak menolak atau tarik menarik
Harga k memiliki hubungan dengan permitivitas relatif medium
 = permitivitas listrik suatu medium
k
1
4..
 = o.r
r = konstanta pembanding/permitivitas relatif medium
o = Permitivitas ruang hampa/udara (8,85 x 10-12 C2.N-1.m-2)
harga k = 9 x 109
Untuk di ruang hampa atau udara
o = 8,85 x 10-12 C2.N-1.m-2
N.m2.C-2 dengan
harga
Cara melukiskan gaya interaksi dua muatan :
1. Dua muatan positif
F12
3. Muatan berlainan jenis
q1
q2
+
+
q1
+
F21
Dua muatan tolak menolak
q2
F12
F21
–
Dua muatan tarik menarik
2. Dua muatan negatif
F12
q1
q2
–
–
F21
Dua muatan tolak menolak
Jika muatan yang berinteraksi lebih dari dua ( misal untuk 3 muatan ), maka Gaya Coulomb total
dicari dengan Resultan dua Vektor yang dirumuskan :
F12 = gaya muatan 1 dengan 2 ( C )
F13 = gaya muatan 1 dengan 3 ( C )
 = sudut antara F12 dan F13 ( ….0 )
F  F  F  2.F12 .F13.Cos
2
12
2
13
contoh lukisan :
–
q3
F13
F

+
q2
+
q1
F12
Soal-Soal :
1.
2.
3.
4.
5.
6.
7.
8.
Dua muatan masing masing 10 C dan 20 C berada pada jarak 20 cm. Tentukan besarnya gaya
Coulomb yang terjadi dari interaksi kedua muatan tersebut !
Dua buah muatan besarnya masing-masing q1 dan q2 berada pada jarak r sehingga menghasilkan
gaya interaksi coulomb sebesar F. Agar gaya interaksinya menjadi ¼.F berapakah jarak antara
kedua muatan tersebut sekarang ?
Dua muatan titik – q dan – 2.q tolak menolak dengan gaya sebesar F. Jika muatan – q coulomb
ditambahkan ke masing masing muatan titik itu, dan jaraknya dijadikan dua kalinya, tentukan gaya
tolaknya sekarang !
Sebuah titik A yang bermuatan 135 C dan titik B bermuatan – 60 C berada pada jarak 10 cm
satu sama lainnya. Muatan C berada di suatu tempat sehingga resultan gaya pada muatan tersebut
sama dengan nol. Tentukan letak muatan tersebut dari titik A.
Dua muatan masing-masing q1 = 10 C dan q2 = 20 C berada pada jarak 20 cm satu sama lainnya.
Dimana muatan ketiga yang besarnya q3 = 5 C diletakkan agar gaya yang dialami muatan ke tiga
tersebut sama dengan nol dilihat dari muatan q1 ?
Pada titik sudut segitiga sama sisi ABC dengan sisi 9 cm terdapat muatan 4 C, 5 C, dan
– 10
C. Tentukan Gaya Coulomb yang bekerja di muatan 4 C !
Tiga buah muatan masing-masing q1 = 10 C, q2 = - 4 C, dan q3 = 12 C, berada pada satu garis
lurus dengan q2 berada di antara dua muatan yang lain. Jarak antara q1 dengan q2 adalah 10 cm, dan
q2 dengan q3 adalah 8 cm. Tentukan resultan gaya coulomb di muatan q2 !
Tiga muatan yang sama terletak pada titik sudut sebuah segitiga sama sisi. Jika gaya antara dua
muatan itu F, tentukan besarnya gaya pada setiap muatan !
B. KUAT MEDAN LISTRIK ( E ) :
Besarnya gaya listrik yang bekerja pada suatu muatan uji sebesar satu satuan muatan listrik :
E
q2 = muatan listrik penguji ( c )
F = Gaya Coulomb ( N )
E = Kuat medan listrik ( N/c )
F
q2
atau setelah dijabarkan diperoleh :
q
E  k. 21
r
q1 = muatan listrik yang diuji ( C )
Kuat medan listrik merupakan besaran vektor yang arahnya :
- searah dengan arah gaya coulomb jika muatan sumber ( + )
- berlawanan arah dengan arah gaya coulomb jika muatan sumber ( - )
Catatan : setiap titik yang berada di dalam medan listrik selalu dianggap bermuatan ( + )
P
+
–
E
P
E
Jika sebuah titik dipengaruhi oleh dua muatan listrik, maka resultan Kuat Medan Listrik dinyatakan :
E1

E  E12  E22  2.E1.E2 . cos 
E2
q1
+
–
q2
Soal Soal :
1. Dua muatan bernilai 8 C dan 12 C berada pada jarak 10 cm. Tentukan :
a. Kuat medan listrik di tengah tengah antara kedua muatan ! (1,4 x 107)
b. Letak titik yang memiliki kuat medan listrik sama dengan nol ! (4,5 cm dari
muatan 1)
2. Pada titik sudut segitiga sama sisi ABC dengan sisi 10 cm terdapat muatan masingmasing 5 C, 5 C, dan –3 C. Tentukan kuat medan di tengah tengah segitiga
(perpotongan garis beratnya) !
Catatan :
Pada garis berat segitiga berlaku perbandingan sisi panjang : sisi pendek = 2 : 1
Atau sisi panjang = 2/3.panjang garis beratnya.
Hukum Gauss :
Untuk menentukan Kuat Medan Listrik (E) yang terdistribusi kontinyu dikembangkan teknik baru
oleh Karl Friedrich Gauss (1777 – 1855).
Pembahasan kita awali dari konsep Fluks Listrik yang didefinisikan : “ jumlah garis-garis medan
listrik yang menembus tegak lurus suatu bidang”
Diilustrasikan :
Bidang Normal
Secara matematis kita dapatkan
hubungan persamaan Fluks Listrik :

Garis gaya listrik
  E. A.Cos 
Bidang yang ditembus
Bidang Normal adalah bidang khayal yang selalu tegak lurus terhadap garis gaya listrik.
Sehubungan dengan Fluks Listrik, Gauss mengemukakan Hukum Gauss yang berbunyi :
“ Jumlah garis gaya medan listrik (fluks listrik) yang menembus suatu permukaan tertutup sama
dengan jumlah muatan listrik yang dilingkupi oleh permukaan tertutup itu dibagi dengan
permitivitas listrik di hampa / udara (0)”
Secara matematis dituliskan :

q
0
atau menjadi
q

E. A.Cos  
0
Keterangan :
 = Fluks Listrik ( Weber) / (Wb)
A = Luas permukaan tertutup (m2)
E = Kuat medan listrik (Wb.m-2)
 = sudut antara bidang dengan bidang normal
q = muatan total yang dilingkupi bidang tertutup ( Coulomb)
0 = permitivitas listrik ruang hampa / udara (C.Wb-1)
Kuat Medan Listrik untuk muatan yang terdistribusi kontinyu :
Dengan menggunakan Hukum gauss kita dapat menentukan Kuat Medan Listrik untuk muatan yang
terdistribusi kontinyu atau seragam seperti pada konduktor dua keping sejajar dan Bola Berongga.
1. Kuat Medan Listrik pada Konduktor dua keping sejajar.
Dua keeping sejajar dengan luas masing-masing A diberi muatan berlawanan +q dan –q, seperti
gambar berikut :
+q
A
E
-q
A
Menurut Hukum Gauss berlaku :
q
E. A.Cos  
0
Dengan  = 0 (bidang sejajar dengan bidang
Normal) atau (bidang tegak lurus medan listrik),
sehingga Cos 0 = 1, dan muatannya q, maka :
q
E. A 
0
Sehingga besarnya Kuat Medan Listrik (E) :
E
q
A. 0
Jika
q
sebagai rapat muatan listrik ()(Sigma) yaitu Muatan listrik tiap satuan luas, diperoleh :
A

q
maka Kuat Medan Listrik dapat dirumuskan :
A
E

0
2. Kuat Medan Listrik pada Bola Berongga
Jika sebuah konduktor berongga kita beri muatan sejenis, maka muatan akan tersebar di seluruh
permukaan konduktor berongga tersebut ( ingat sifat muatan sejenis tolak menolak),
diilustrasikan sebagai berikut :
II
+ + +
+
++
R +
+
+ I
+
+
+
+
+
r<R
+
+
+
+
+
+ + + + ++
r>R
a. Kuat Medan Listrik di dalam bola konduktor
Perhatikan permukaan Gauss I yang melingkupi tempat di dalam bola berongga, dimana di
dalamnya tidak ada muatan listrik yang dilingkupi, sehingga menurut Hukum Gauss berlaku :
q
q
E. A 
sehingga E 
dengan q = 0 ,
maka E = 0
0
A. 0
b. Kuat Medan Listrik di permukaan bola (r = R) sampai dengan titik berjarak r (r > R )
Perhatikan permukaan Gauss II yang melingkupi tempat di luar bola berongga, dimana di
dalamnya terdapat muatan listrik q yang dilingkupi, sehingga menurut Hukum Gauss berlaku
persamaan :
q
E
dengan A = 4..r2 (Luas permukaan bola), sehingga diperoleh
A. 0
persamaan :
1 q
E
4.. 0 r 2
1
k
dengan
4. . 0
sehingga
E  k.
q
r2
Jika dibuatkan grafik hubungan E dengan r, diperoleh seperti di bawah ini :
E
E=0
r
r=R
r=0
C. ENERGI POTENSIAL LISTRIK ( Ep ) :
Besarnya usaha untuk memindahkan suatu muatan listrik dari jauh tak terhingga ke titik di dalam
medan listrik.
W = F. r
W = Ep = F. r
Untuk perubahan yang kecil di cari dengan mengintegralkan persamaan di atas menjadi :
r2
W   F .dr
r1
r2
q .q
W   k . 1 2 2 .dr
r
r1
r2
W  k .q1.q2 . r  2 .dr
r1
r2
W  k .q1 .q2 .
r1
1
.dr
2
r
r
1 2
W  k .q1.q2 . 
r  r1
1
1
W   k .q1.q2 .  
 r2 r1 
Jika muatan dipindahkan ke jauh tak terhingga, r2 =
Listrik di titik asal muatan. Sehingga :
,
besar Usaha sama dengan Energi Potensial
1 1
W   k .q1 .q 2 .  
  r1 

1
W   k .q1.q2 .0  
r1 

Hasilnya :
W  k.
Dengan W
q1 .q 2
r
= Ep , Untuk itu diperoleh :
Ep = Energi Potensial listrik ( J )
r = jarak titik terhadap muatan ( m )
q1 = muatan listrik yang di uji ( C )
q2 = muatan penguji ( C )
Energi Potensial listrik adalah besaran skalar, sehingga tanda (+) atau (-) dari muatan di tuliskan apa
adanya dalam persamaan.
q .q
E p  k. 1 2
r
D. POTENSIAL LISTRIK ( V ) :
Besarnya Usaha untuk memindahkan satu satuan muatan penguji dari titik tak terhingga ke suatu
titik di dalam medan listrik.
Ep
V
q2
Maka diperoleh :
q1 = muatan yang diuji ( yang mempe ngaruhi muatan uji ( C )
q1
V = potensial listrik ( Volt )
V  k.
r
Potensial listrik dari beberapa muatan listrik merupakan jumlah dari masing masing potensial listrik.
V
= V1 + V2 + V3 + …..
(penjumlahan skalar)
atau :
 q1
V  k  r


q 2 q3
  ....
r2 r3

 1
q1, q2, q3 = muatan yang mempengaruhi suatu titik dan tanda (+) atau (- ) dari muatan di
masukkan apa adanya.
r1 , r2 , r3 = jarak masing masing muatan ke suatu titik ( m )
Potensial Listrik pada Konduktor Bola Berongga :
Perhatikan bola berongga di bawah ini :
q
B
R
D
C
r>R
r<R
Bola berongga dengan jari-jari R dimuati dengan muatan +q tersebar merata di
permukaan bola tersebut.
Pada materi sebelumnya telah dibuktikan bahwa di dalam bola (r < R) berlaku E = 0.
Usaha untuk memindahkan muatan listrik dari titik C ke titik D (mewakili titik di dalam
bola berongga) :
WCD = q. VCD menjadi WCD = q. (VD – VC) ...................... *
Usaha juga dapat dituliskan sebagai :
WCD = F. CD ( hasil kali gaya dengan perpindahan)
Dengan F = q.E ( hubungan gaya dengan kuat medan listrik), maka
WCD = q.E.CD
Karena untuk r < R berlaku E = 0, maka
WCD = q.0.Cd
WCD = 0 ............................................. **
Jika pers * digabung dengan pers **, maka diperoleh :
0 = q. (VD – VC)
Sehingga secara matematis dapat dinyatakan :
q = 0 ( tak mungkin) atau VD – VC = 0
Sehingga :
VD = VC
Artinya :
Bahwa Potensial listrik di dalam bola konduktor sama dengan potensial listrik di
permukaan bola konduktor tersebut.
Kondisi ini dapat dikatakan bahwa bidang di dalam bola berongga adalah “Bidang
Ekipotensial” yaitu bidang dimana setiap titik di dalam bidang tersebut memiliki
potensial listrik yang sama.
q
r
Untuk titik berjarak r  R tetap berlaku : V  k . , sehingga dapat disimpulkan :
a. Di luar bola ( r > R ) :
b.
V  k.
q
r
V  k.
Di Kulit bola dan di dalam bola ( 0  r  R ) :
q
R
Secara grafik dapat kita lukiskan :
V
r=0
r=R
r
Soal soal :
1. Dua buah muatan
4 C dan 6 C berada pada jarak 20 cm satu dengan lainnya. Berapakah
Energi Potensial yang terjadi antara dua muatan tersebut !
2. Tentukan potensial di suatu titik yang berjarak 2 cm dan 4 cm dari suatu muatan titik sebesar q =
0,5 C !
3. Pada titik sudut segitiga samasisi ABC dengan sisi 10 cm, terdapat muatan - 13C, 6 C, dan 2 C.
Hitunglah :
a. potensial di titik E yang berada di tengah tengah AB dan titik F ditengah tengah BC !
b. Usaha orang untuk memindahkan muatan – 2 C dari titik E ke titik F !
4. Hitung Usaha yang diperlukan untuk memindahkan muatan 4 C dari titik yang berjarak 20 cm ke
titik yang berjarak 6 cm dari muatan 10 C !
Tambahan :
Hubungan antara Energi Potensial dengan Potensial Listrik :
Ep = q2 . V
Usaha untuk memindahkan muatan dari dua titik yang berpotensial berbeda adalah :
W = Ep
maka W = q2. V
atau
Hubungan Potensial Listrik dengan Gaya Coulomb :
F
Hubungan Gaya coulomb dengan Energi Potensial Listrik :
W  q2 V2  V1 
q2 .V
R
F
Ep
R