penggunaan determinan polinomial matriks dalam modifikasi

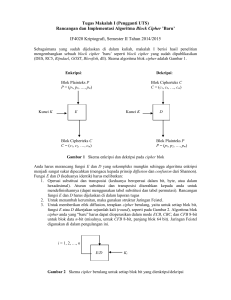
PENGGUNAAN DETERMINAN POLINOMIAL MATRIKS DALAM
MODIFIKASI KRIPTOGRAFI HILL CHIPER
Alz Danny Wowor
Jurusan Teknologi Informasi Fakultas Teknologi Informasi Universitas Kristen Satya Wacana
Jl. Diponegoro 50-66, Salatiga, 50711
Telp : (0298) 3419240, Fax : (0298) 3419240
E-mail: [email protected]
Abstrak
Hill cipher mengenkripsi pesan menggunakan matriks sebagai kunci, yang dapat digunakan
sebagai pengamanan informasi. Teknik kriptografi ini telah dipecahkan dengan kriptanalisis known
plaintext attack. Penelitian ini memodifikasi Hill cipher menggunakan kunci yang dibangkitkan dari
determinan polinomial matriks. Hasil diperoleh bahwa modifikasi Hill cipher memenuhi syarat sistem
kriptografi. Proses enkripsi-dekripsi membutuhkan rata-rata waktu 0,068 detik lebih lama dari Hill cipher
dan membutuhkan rata-rata memori lebih banyak 0,102M. Modifiaksi yang dilakukan dapat menahan
serangan kriptanalisis yang sebelumnya dapat membobol Hill cipher.
Kata Kunci: Hill Cipher, Known Plaintext Attack, Determinan Polinomial Matriks
Pendahuluan
Penggunaan kriptografi sebagai pengamanan terhadap transfer informasi menjadi
perhatian yang serius. Banyak kasus penyadapan, pembobolan email dan lain sebagainya
membuat menempatkan kriptografi pada peranan yang penting. Banyak kasus yang terjadi
akibat dari lemahnya sebuah sistem pengamanan sehingga informasi penting baik secara
pribadi maupun organisasi jatuh ke pihak yang tidak berwajib.
Seiring dengan berjalannya waktu kriptografi pun mengalami masalah dalam
mengamankan informasi bila hanya mengandalkan kriptografi standart, yang mempunyai
kemungkinan sudah ada kriptanalisisnya. Oleh karena itu, sangat diperlukan teknik yang baru
atau memodifikasi teknik yang sudah ada untuk dapat meningkatkan keamanan informasi
tersebut.
Tulisan ini memodifikasi kriptografi Hill Cipher (HC) yang mengandalkan matriks
sebagai kunci dalam melakukan proses enkripsi maupun dekripsi. Penggunaan kunci tambahan
berupa determinan dari matriks polinomial berupa persamaan polinomial yang digunakan
sebagai pembangkit kunci. Selain itu juga digunakan convert between base (CBB) yang
mengkonversi setiap bilangan ke basis bilangan yang lainnya.
Studi Pustaka
Hill Cipher
Hill Cipher adalah kriptografi yang menggunakan matriks sebagai kunci. Proses Hill
cipher ditunjukkan pada Gambar 1.
Gambar 1. Proses Enkripsi-Dekripsi Hill Cipher (Alz, 2013)
Matriks bujursangkar Ω berordo 𝑛 × 𝑛 yang mempunyai invers untuk dijadikan kunci.
Misalkan P sebagai plainteks yaitu dan C sebagai cipherteks sehingga proses enkripsi adalah
(Stanoyevitch, 2011)
𝐶 = Ω ∙ 𝑃 (𝑚𝑜𝑑 26)
(1)
Proses dekripsi secara umum diberikan
𝑃 = Ω−1 ∙ 𝐶 (𝑚𝑜𝑑 26)
(2)
Matriks Polinomial
Jika A adalah sebuah matriks bujursangkar, misalnya m × m, dan jika
𝑝(𝑥) = 𝑎0 + 𝑎1 𝑥 + ⋯ + 𝑎𝑛 𝑥 𝑛
adalah polinomial sembarang. Untuk setiap koefisien 𝑎0 sampai 𝑎𝑛 dari Persamaan (3),
digantikan dengan 𝑛 matriks yang secara umum dapat didefenisikan sebagai
𝑝(𝑥) = 𝐴0 + 𝐴1 𝑥 + ⋯ + 𝐴𝑛 𝑥 𝑛
(3)
(4)
Convert Between Base
Convert Between Base (CBB) merupakan suatu proses yang mengubah urutan bilangan
dari satu basis ke basis yang lainnya. Untuk menjelaskan proses cari CBB maka diberikan
dengan kedua defenisi berikut ini.
Defenisi 1. (Maplesoft, 2010) Konversi sembarang bilangan positif s berbasis 10 ke basis β.
Secara umum notasinya,
Konv (s, base β ).
Defenisi 2. (Maplesoft, 2010) Konversi dari urutan bilangan (list digit) ℓ dalam basis α ke
basis β, dinotasikan,
Konv (ℓ, α base β )
nops(ℓ)
dengan jumlahan urutan bilangan (jumlahan ℓ) mengikuti aturan,
å
I k × a k-1
i=1
dimana nops (ℓ) adalah nilai terakhir dari urutan bilangan ℓ.
• 0 ≤ Ik ≤ α dan ℓ adalah bilangan positif.
• Nilai yang diperoleh merupakan kumpulan urutan bilangan dalam basis β.
Metodologi Penelitian
Penelitian ini memodifikasi kriptografi Hill cipher menggunakan determinan dari
matirks polinomial. Perlu untuk disiapkaan sembarang matriks bujur sangkar yang mempunyai
invers. Kemudian hasil dari determinan matriks tersebut dijadikan sebagai kunci yang
dibangkitkan dari fungsi polinomial.
Berikut langkah-langkah analisis yang dilakukan untuk mencapai tujuan penelitian
yaitu, memodifikasi Hill cipher dan menguji modifikasi tersbut terhadap serangan kriptanalisis
known plaintext attack, secara lengkap diberikan pada Gambar 2.
Gambar 2. Langkah Penelitian
Berdasar pada Gambar 2, Langkah ke-2 adalah Modifikasi Hill cipher. Bagian ini
menujukan perancangan modifikasi. Menyiapkan plainteks yang akan di enkripsi, setelah itu
adalah pembangkitan kunci dari fungsi polinomial dari sembarang matriks bujursangkar.
Fungsi yang diperoleh kemudian disubtitusikan dengan konstanta bilangan bulat sehingga
menghasilkan bilangan unik yang dapat dijadikan sebagai koefisien pada sejumlah persamaan
linier (f1, f2, ..., fn). Selanjutnya kunci yang dimasukan akan di ubah menjadi sederetan angka
menggunakan konversi ASCII, yang membentuk n-matriks kunci (M1, M2, ..., Mn), seperti pada
Gambar 3.
Gambar 3. Proses Enkripsi
Proses dekripsi dilakukan dengan plainteks dikonversi ke ASCII, setelah itu dilakukan
proses CBB seperti yang diberikan pada Defenisi 2, hasil dari CBB kemudian di kalikan dengan
matriks kunci (M1) dan kemudian di subtitusikan ke dalam persamaan linier (f 1) yang
menggunakan konstanta unik. Hasil tersebut dianggap sebagai (C1) atau ciphertext yang
pertama. Selanjutnya dilakukan proses yang sama untuk mendapatkan ciphertext ke-n (Cn),
setelah itu prose yang terakhir adalah dilakukan konverai antar basis bilangan (Bs-2) untuk
mendapatkan ciphertext.
Gambar 4. Proses Dekripsi
Setiap matriks yang dijadikan kunci adalah matriks yang mempunyai invers, sehingga
dalam proses dekripsi dapat juga dikembalikan ke plantext. Gambar 3, menujukkan proses
untuk mengembalikan pesan dilakukan dengan mengkonversi kembali dengan invers dari CBB
yang kedua (Inv-Bs 2) kemudian dengan fungsi linier yang terakhir (fn), hasilnya dikalikan
dengan invers matriks (Mn-1). Proses ini dilakukan terus menerus sampai dengan perkalian
fungsi terakhir (f1) dan M1, hasil tersebut di konversi dengan InvBs-1 sehingga diperoleh
plaintext.
Hasil dan Pembahasan
Modifikasi kriptografi Hill cipher diuji dengan mengenkripsi sebuah palinteks yaitu
“salatiga hati beriman” dan kunci yang digunakan adalah “fti uksw”. Selain juga perlu
disiapkan beberapa matriks yang digunakan sebagai pembangkit kunci fungsi linier, matriks
tersebut adalah
1
𝐴 = [−30
60
30
1
0
0
0.1822
0.0088
2] , 𝐵 = [ 0.0141
0.2769
1
−0.0966 −0.0435
0.0033 −0.0082 0.0495
𝐶 = [0.3444 0.2730 0.2246]
0.0845 0.0379 0.0733
0.011
0.1035],
0.4876
Dari ketiga matriks di atas, disubtitusikan ke Persamaan (5), dengan A0 = A, A1 = B, dan A2 =
C, maka akan diperoleh sebuah matriks
1 − 0.1822𝑥 − 0.0033𝑥 2
𝐷𝐸 = [−30 − 0.0141𝑥 − 0.3444𝑥 2
60 + 0.0966𝑥 − 0.0845𝑥 2
30 − 0.0088𝑥 + 0.0082𝑥 2
1 − 0.2769𝑥 − 0.2730𝑥 2
0.0435𝑥 − 0.0379𝑥 2
−0.011𝑥 − 0.0495𝑥 2
2 − 0.1035𝑥 − 0.2246𝑥 2 ]
1 − 0.4876𝑥 − 0.0733𝑥 2
Selanjutnya adalah mencari determinan dari matriks DE, sehingga diperoleh
persamaan polinomial
𝑓(𝑥) = 4501 − 620.6147𝑥 − 461.2591221𝑥 2 − 6.251018198𝑥 3 − 1.203136772𝑥 4 −
0.003379045028𝑥 5 + 0.000406454158𝑥 6
(5)
Persamaan (5) menjadi pembangkit kunci untuk mendapatkan koefisien untuk fungsi
rasional yang digunakan (f1 sampai fn). Selanjutnya untuk mencari matriks kunci (M1 sampai
Mn) digunakan kunci yang diinput. Misalnya dalam kasus ini adalah digunakan 3 matriks yang
dibangkitkan dari kunci “fti uksw”, maka diperoleh
30
0
112
1
2
30
73
2
30
𝑀1 = [ 7 108
3 ] , 𝑀2 = [26 108 3 ] , 𝑀3 = [ 3 108 73]
0
52
2
21 52
2
5 104 2
Selain menggunakan determinan dari polinomial matriks dan matriks kunci,
perancangan kriptografi ini juga menggunakan CBB untuk proses awal dan akhir, pada kasus
ini berdasarkan Defenisi 2, maka untuk Bs-1 digunakan 𝛼 = 127 dan 𝛽 = 7 dan Bs-2 dipilih
𝛼 = 131 dan 𝛽 = 2 . Setelah kunci yang digunakan telah tersedia, proses enkripsi dapat
dilakukan dengan menggunakan plaintext “salatiga hati beriman” diperoleh ciphertext
"1110110001101011101011100101"
Untuk proses dekripsi dilakukan dengan menggunakan CBB untuk Bs-2 sedangkan
basis untuk Bs-1, proses untuk setiap iterasi dilakukan perkalian dengan invers dari setiap
matiks. Sehingga akan diperoleh kembali palainteks “salatiga hati beriman”. Berdasarkan
proses yang telah ditunjukkan, modifikasi kriptografi Hill cipher dapat melakukan proses
enkripsi-dekripsi, secara umum dapat dikatakan sebagai sebuah teknik kriptografi.
Menjadi sebuah teknik kriptografi tidak hanya dapat melakukan proses enkripsidekripsi, tetapi harus memenuhi 5-tuple yang disyaratkan oleh Stinson. Sebuah sistem
kriptografi harus memenuhi 5 tuple P, C, K, E, D. Oleh karena itu akan ditunjukan modifikasi
ini memenuhi kelima kondisi tersebut (Stinson, 1995). P adalah himpunan berhingga dari
plainteks. Dalam modifikasi Hill cipher menggunakan 127 karakter maka himpunan plainteks
pada modifikasi Hill Cipher adalah himpunan berhingga.
C adalah himpunan berhingga dari cipherteks. Cipherteks dihasilkan dalam elemen
bit biner (bilangan 0 dan 1). Karena hipunanan cipherteks hanya {0,1}, maka cipherteks
modifikasi Hill Cipher adalah himpunan berhingga. K merupakan ruang kunci (keyspace),
adalah himpunan berhingga dari kunci. Kunci tambahan dalam modifikasi Hill Cipher adalah
fungsi linier dan Konversi Basis Bilangan yang juga himpunan berhingga. Untuk setiap 𝑘 ϵ 𝐊,
terdapat aturan enkripsi ek ϵ 𝐄 dan berkorespodensi dengan aturan dekripsi dk ϵ 𝐃. Setiap ek ∶
𝐏 ⟶ 𝐂 dan dk ∶ 𝐂 ⟶ 𝐏 adalah fungsi sedemikian hingga 𝑑𝑘 (𝑒𝑘 (𝑥)) = 𝑥 untuk setiap
plainteks 𝑥 ϵ 𝐏. Kondisi ke-4 ini, terdapat kunci yang dapat melakukan proses enkripsi
sehingga merubah plaintext menjadi ciphertext. Dan dapat melakukan proses dekripsi yang
merubah ciphertext ke plaintext. Karena memenuhi ke-lima kondisi maka modifikasi pada Hill
Cipher merupakan sebuah sistem kriptografi.
Perbandingan dengan Hill Cipher
Proses enkripsi-dekripsi yang dibandingkan adalah ketersediaan plainteks,
ketersediaan banyaknya matriks kunci yang dapat dibentuk dan tentu juga untuk invers matriks
kunci. Ruang sampel yang dapat digunakan untuk plainteks. Plaintext yang dapat dibentuk
untuk Modifikasi sebanyak 127 karakter yang disesuaikan dengan ASCII, tetapi untuk Hill
cipher hanya tersedia 26 karakter. Berdasarkan aturan perpangkatan diperoleh modifikasi Hill
Cipher mengungguli Hill Cipher sebanyak 3.298105963 × 10229 kali.
Matriks kunci yang tersedia diambil berdasarkan bilangan yang bersesuaian karakter
plainteks (26 pada Hill Cipher dan 127 dalam modifikasi). Entri matriks bergantung pada ordo
matriks kunci. Perbandingan banyak matriks yang dapat dijadikan kunci diberikan pada Tabel
1, dibawah ini.
Tabel 1. Perbandingan Ketersediaan Matriks Kunci (Alz, 2013)
Ordo
Matriks
(𝑘
× 𝑘)
2x2
3x3
4x4
Banyak
entri
(𝑘 2 )
HC (𝑘 = 26)
MHC (𝑘 = 127)
4
9
16
14950
3124550
5311735
10334625
17722355795375
81675143551104405225
Banyak Kombinasi matriks yang diperoleh
Perbandingan
(Hc : MHc)
1 : 691.279
1 : 5.672 × 106
1 : 1.538 × 1013
Invers matriks digunakan untuk proses enkripsi baik pada Hill Cipher dan Modifikasi
Hill Cipher. Invers dari matriks, terlebih dahulu dilihat determinan yang mempunyai resiprok
(invers perkalian) terhadap 𝐙𝟐𝟔 dan 𝐙𝟏𝟐𝟕 . Hill cipher, matriks kunci tidak bisa memiliki nilai
determinan genap, 0 dan 13 karena tidak memiliki resiprok terhadap modulo 26. Sedangkan
Modifikasi Hil Cipher, hanya determinan 0 saja yang tidak memiliki resiprok terhadap modulo
127. Shingga banyak peluang determinan dari matriks kunci yang mempunyai resperiok, maka
untuk Hill Cipher diperoleh 0,538, dan pada Modifikasi diperoleh 0.992. Peluang untuk matriks
yang tidak mempunyai invers sebesar 0,462 = (1 – 0,538) untuk Hill cipher, sehingga perlu
lebih hati-hati dan teliti untuk mengambil matriks kunci. Sedangkan untuk untuk Modifikasi
Hill Cipher hampir mendekati satu (yaitu 0.992). Sehingga pengambilan matriks yang dapat
dijadikan kunci sangat bebas. Hal ini juga dapat ditunjang dengan peluang matriks yang tidak
mempunyai invers sangat kecil hanya sekitar 0.008 = (1 – 0.992).
Kriptananlisis Pada Modifikasi Hill Cipher
Kriptografi Hill cipher telah dipecahkan dengan teknik Kriptanalisis known-plaintext
attack (Anton & Rorres, 2005). Perkalian matriks merupakan suatu kombinasi liner, sehingga
pola dari setiap cipherteks dengan plainteks dapat diketahui. Hal ini dipermudah dengan relasi
plainteks dan cipherteks adalah Z26 ke Z26. Oleh karena itu perkalian matriks dapat dilakukan
dan matriks kunci dapat ditemukan. Modifikasi Hill cpher ini, dirancang dengan plainteks
dalam Z127 ke cipherteks dalam Z2, relasi ini mempersulit kriptananlisis untuk dapat melihat
pola yang semula mudah ditemukan. Hal ini dipersulit dengan penggunaan perkalian n-matriks
kunci dan proses CBB. Sehingga kriptanalisis known-plaintext attack dengan perkalian matriks
tidak dapat menumukan matriks kunci (apalagi ada n-matriks kunci).
Kebutuhan Waktu dan Memori
Kebutuhan akan waktu dan memori pada setiap kriptografi sangat diperlukan untuk
melihat perbandingan antara Hill Cipher (HC) dan Modifikasi Hil Cipher (MHc). Gambar 4
menunjukkan MHc membutuhkan memori dan waktu yang lebih banyak dari HC. MHc
memerlukan rata-rata memori 0,102 M lebih banyak dari HC. Sedangkan untuk kebutuhan
waktu berdasarkan banyak karakter MHc memerlukan rata-rata waktu 0,068 detik lebih banyak
dibandingkan dengan HC.
Lebih banyak kebutuhan waktu dan memori karena dalam proses yang dilakukan,
terdapat beberapa fungsi ditambahkan untuk memperkuat proses kriptografi. Hal ini
berimplikasi pada kekuatan algoritma terhadap kriptanalisis known-plaintext attack (KPA)
yang sebelum memecahkan Hill Cipher.
2.5
0.2
0.18
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
Waktu (s)
Memori (M)
2
1.5
1
0.5
0
0
100
200
300
400
Banyak Karakter
Hil Cipher
Modifikasi
500
0
100
200
300
400
500
Banyak Karakter
Hill Cipher
Modifikasi
Gambar 4. Kebutuhan Memori dan Waktu
Kesimpulan
Perancangan modifikasi kriptografi Hill cipher menggunakan determinan polinomial
matriks dapat dapat memenuhi syarat untuk menjadi sebuah sistem kriptografi. Penggunaan
kunci dari determinan polinomial matriks memberikan perubahan yang signifikan pada
algoritma dari sisi keamanan, karena dapat menahan serangan kriptanalisis known-plaintext
attack yang sebelumnya membobol Hill cipher. Kelebihan menahan kriptanalisis memebrikan
dampak pada modifikasi Hill cipher dalam proses enkripsi-dekripsi membutuhkan waktu ratarata 0,068 detik lebih lama dari Hill cipher, sedangakan untuk rata-rata kebutuhan memori lebih
banyak 0,102M.
Daftar Pustaka
Alz Danny Wowor, 2013, Modifikasi Kriptografi Hill Cipher Menggunakan Convert Between
Base, Seminar Nasional Sistem Informasi Indonesia (SESINDO), Bali 2-4 Desember
2005, ITS Surabaya.
Anton, H. & Rorres, C., 2005, Elementary Linear Algebra, Applications Version, 9th Edition,
New York: John Wiley & Sons.
Hill, Lester, S., 1929, Cryptography in an Algebraic Alphabet: The American Mathematical
Monthly, 36 (6), pp.306-312.
Stinson, D.R., 1995, Cryptography Theory and Practice, Florida: CRC Press, Inc.
Stanoyevitch, A., 2011, Introduction to Cryptography with Mathematical Foundations and
Computer Implementations, Boca Raton-Florida: Chapman & Hall/CRC Taylor &
Francis Group.