Penggunaan Integral dalam Keteknikan dan Ekonomi

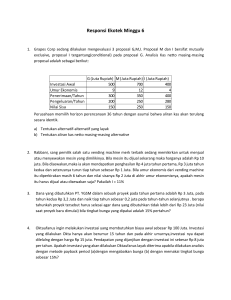
PENGGUNAAN INTEGRAL DALAM KETEKNIKAN DAN EKONOMI
DIGUNAKAN UNTUK MEMENUHI TUGAS AKHIR MATEMATIKA INDUSTRI
Oleh :
MARISA AMALIA
125100301111076
TEKNOLOGI INDUSTRI PERTANIAN
FAKULTAS TEKNOLOGI PERTANIAN
UNIVERSITAS BRAWIJAYA
MALANG
2013
Penggunaan Integral dalam Keteknikan dan Ekonomi
Penerapan integral dalam kehidupan sehari-hari sangat luas. Aplikasi integral banyak
digunakan di berbagai disiplin ilmu. Beberapa contoh penggunaan integral dalam disiplin ilmu
alam adalah digunakan dalam bidang biologi untuk menghitung laju pertumbuhan organisme,
dalam bidang fisika untuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung
laju pemisahan, dan dalam bidang keteknikan. Tidak hanya itu, integral juga digunakan dalam
disiplin ilmu sosial yang berupa penerapan dalam bidang bisnis dan ekonomi.
Penggunaan integral dalam keteknikan adalah sebagai berikut :
1. Solusi masalah transport polutan dalam medium anisotropik
Solusi masalah transport polutan dalam medium anisotropik adalah dengan
metode elemen batas. Metode inimenggunakan dasar persamaan integral
batas, dengan mentransformasi persamaan pengatur menjadi persamaan
integral.
Persamaan pengatur :
Persamaan integral :
2. Penyelesaian pada sistem elektronik
 Pada arus DC
t=0
E
R
L
 Pada arus AC biasa
Sebuah arus sinusoidial biasa dapat ditulis sebagai berikut
Maka besarnyategangan pada komponen elektronik menjadi
3. Untuk menghitung volume
Penggunaan integral dalam ekonomi adalah sebagai berikut :
1. Dari fungsi marginal ke fungsi total
Bila diketahui fungsi total (misalnya, fungsi total biaya), proses diferensiasi
dapat menghasilkan fungsi marginal (misalnya, fungsi biaya marginal).
Karena proses integrasi merupakan kebalikan dari diferensiasi, hal ini,
sebaliknya akan memungkinkan kita untuk mencari fungsi total dari fungsi
marginal tertentu.
Contoh soal :
Jika biaya marginal (MC) suatu perusahaan merupakan fungsi output C'(Q) =
2e0,2Q, dan jika biaya tetap adalah CF = 90, carilah fungsi biaya total C(Q).
Dengan mengontegrasikan C'(Q) terhadap Q, kita dapatkan bahwa
Hasil ini dapat digunakan sebgai fungsi C(Q) yang diinginkan kecuali,
mengingat konstanta arbiter c, jawabannya timbul tanpa ditentukan.
Untungnya, informasi bahwa CF = 90 dapat digunakan sebagai kondisi awal
untuk menetapkan konstanta. Bila Q = 0, total biaya C hanya akan terdiri dari
CF. oleh karena itu, dengan menetapkan Q = 0 dalam hasil di atas, kita akan
dapatkan nilai 90; yaitu 10e0 + c = 90. Tetapi ini akan berarti bahwa c = 90 –
10 = 80. Jadi, fungsi total biaya adalah
2. Investasi dan pembentikan modal
Pembentukan modal adalah proses penjumlahan persediaan atau stok modal.
Dengan menganggap proses ini sebagai proses yang kontinu sepanjang
waktu, kita bisa menyatakan persediaan modal sebagai suatu fungsi waktu,
K9t),
dan
menggunakan
derivatif
untuk
menunjukkan
tingkat
pembentukan modal. Tetapi tingkat pembentukan modal pada waktu t adalah
identik dengan tingkat arus investasi netto pada waktu t, yang ditunjukkan
dengan l(t). jadi persediaan modal K dan investasi netto l dihubungkan
dengan dua persamaan berikut
dan
Persamaan pertama merupakan suatu identitas yang menunjukkan sinonimitas
antara investasi netto dan pertambahan modal. Karena l(t) adalah K(t), maka
beralasan bahwa K(t) merupakan integral atau antiderivatif dari l(t), seperti
ditunjukkan dalam persamaan kedua. Transformasi integran dalam persamaan
yang terakhir juga mudah untuk dipahami : Peralihan dari l ke
adalah
menurut definisi, dan transformaasi selanjutnya adalah dengan pembatalan
dua diferensial yang identik, yaitu menurut aturan subtitusi. Kadang-kadang
konsep investasi bruto digunakan bersama dengan investasi netto dalam
model. Dengan menunjukkan investasi bruto dengan lg dan investasi netto
dengan IlI, kita dapat menghubungkannya satu sama lain dengan persamaan
dimana δ menggambarkan tingkat penyusutan modal dan δK
tingkat investasi pengganti.
Contoh soal :
Jika investasi netto merupakan arus konstan pada l(t) = 1000 (dollar per
tahun), berapakah total investasi netto (pembentukan modal) selama satu
tahun, dari t = 0 ke t = 1 ?
Jelas jawabannya adalah $1000; ini dapat diperoleh secara formal sebagai
berikut :
3. Nilai sekarang dan arus kas
Contoh soal :
Berapakah nilai sekarang dari arus pendapatan kontinu yang berlangsung
selama y tahun pada tingkat yang konstan sebesar D dollar per tahun dan
didiskontokan pada tingkat r per tahun ?
Terdapat persamaan
Jadi Π tergantung pada D, r dan y. bila D = $3.000, r = 0,06 dan y = 2,
misalnya, kita memperoleh
Nilai Π biasanya selalu positif, ini sesuai dengan positivitas D dan r serta
. Bilangan e yang mempunyai pangkat negatif akan selalu
memberikan nilai pecahan yang positif.
4. Nilai sekarang dan arus perpetual
Jika arus kas berlangsung selamanya―suatu situasi yang dicontohkan oleh
bunga atas obligasi perpetual atau pendapatan atas aktiva modal yang tak
dapat rusak seperti tanah―nilai sekarang dari arus kas akan menjadi
yang merupakan integral tak wajar.
Contoh soal :
Carilah nilai sekarang dari aliran pendapatan perpetual yang mengalir pada
tingkat yang seragam sebesar D dollar per tahun, bila tingkat diskonto
kontinu adalah r. karena, dalam mengevaluasi integral tak wajar, kita cukup
mengmbil limit integral tak wajar. Secara khusus, kita dapat menulis
Perhatikan bahwa parameter y (jumlah tahun) telah hilang dari jawaban akhir.
Hal ini memang seharusnya terjasi, karena di sini kita menghadapi arus
perpetual. Dapat juga diamati bahwahasil yang didapat (nilai sekarang =
tingkat arus pendapatan + tingkat diskonto) secara tepat berhubungan dengan
rumus yang lazim disebut “kapitalisasi” dari suatu aktiva dengan hasil
perpetual.
5. Menentukan persamaan harga dan permintaan
6. Menentukan persamaan harga dan penawaran
7. Menentukan fungsi biaya
Contoh soal :
Biaya marginal suatu perusahaan ditunjukkan oleh MC = 3Q – 6Q + 4.
Carilah biaya total dan biaya rata-ratanya.
Biaya total merupakan integrasi dari biaya marginal
. Soal ini dapat diselesaikan dengan :
Biaya total :
Biaya rata-rata :
konstanta k adalah biaya tetap
8. Menentukan fungsi pendapatan
Contoh soal :
Carilah persamaan penerimaan total dan penerimaan rata-rata dari suatu
perusahaan jika penerimaan marginalnya MR = 16 – 4Q.
Penerimaan total merupakan integral dari penerimaan marginal
. Soal ini dapat diselesaikan dengan :
Penerimaan total :
Penerimaan rata-rata :
dalam persamaan penerimaan total, konstanta k = 0, sebab penerimaan tidak
ada jika tidak ada barang yang dihasilkan atau barang yang terjual.
Daftar Pustaka
Chiang,
Alpha C.
Wainwright,
Kevin.
2005.
FUNDAMENTAL
METHODS OG
MATHEMATICAL ECONOMICS, 4TH ED. London : McGraw-Hill, Inc.
Listya, Tri Dewi dan Herawati. 2007. MATEMATIKA, Buku Pelajaran untuk SMA Kelas
XII.Bandung : Grafindo Media Pratama.
Sahari, Agusman. 2011. METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT.
JIMT, Vol.8 , No.1
Wanda.
2010.
Aplikasi
Integral
Tak
Tentu
Dalam
Ekonomi.
http://wanday-
doanx.blogspot.com/2010/01/aplikasi-integral-tak-tentu-dalam.html
pada 28 Desember 2012 pukul 19:00 WIB.
Diakses