SISTEM LINIER_BAB I_b kecil _1

1.1. Pendahuluan
Teori dan konsep sinyal diperlukan pada bidang rekayasa kelistrikan
dan bidang teknik lainnya. Dalam bab ini diperkenalkan tentang pengertian
sinyal serta klasifikasinya. Beberapa sinyal dasar yang penting serta operasi
dasar sinyal juga dibahas dalam bab ini.
1.2. Pengertian Sinyal
Secara umum, sinyal didefinisikan sebagai suatu besaran fisis yang
merupakan fungsi waktu, ruangan atau beberapa variable. Contoh dari sinyal
adalah sebagai berikut:
 Tegangan listrik (V) sebagai fungsi waktu
 Suhu ruangan fungsi waktu
 Potensial listrik fungsi dari posisi pada suatu ruang 3 dimensi
 Intensitas sebagai fungsi koordinat x, y dan waktu
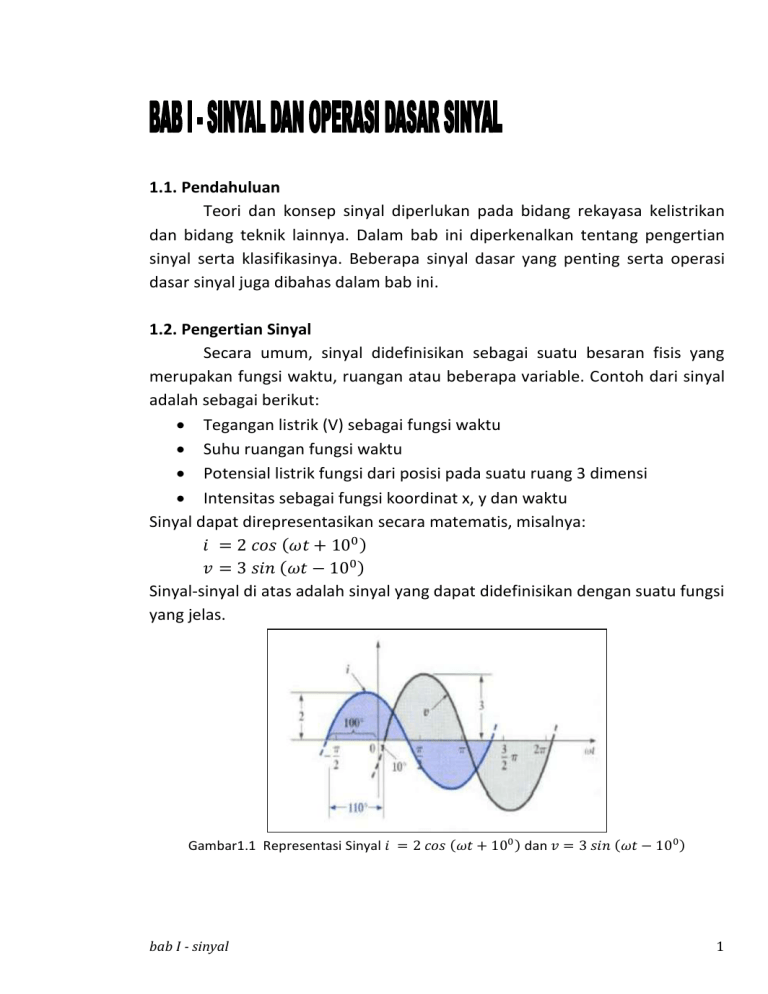
Sinyal dapat direpresentasikan secara matematis, misalnya:
𝑖 = 2 𝑐𝑜𝑠 (𝜔𝑡 + 100 )
𝑣 = 3 𝑠𝑖𝑛 (𝜔𝑡 − 100 )
Sinyal-sinyal di atas adalah sinyal yang dapat didefinisikan dengan suatu fungsi
yang jelas.
Gambar1.1 Representasi Sinyal 𝑖 = 2 𝑐𝑜𝑠 (𝜔𝑡 + 100 ) dan 𝑣 = 3 𝑠𝑖𝑛 (𝜔𝑡 − 100 )
bab I - sinyal
1
Dalam beberapa kasus, sinyal tidak dapat dilihat hubungan fungsinya secara
nyata dan sangat kompleks. Contohnya sinyal pembicaraan seperti terlihat
pada Gambar 1.2.
Gambar 1.2 Contoh Sinyal Suara
Sinyal suara pada Gambar 1.2 dapat dituliskan sebagai fungsi
penjumlahan dari gelombang sinus dengan amplitude berbeda:  Ai = sin
[2Fi(t) + i(t)].
Sinyal mempunyai beberapa jenis informasi yang dapat diamati
misalnya amplitudo, frekuensi, perbedaan fasa dan gangguan akibat noise.
Untuk mengamati informasi tersebut, dapat digunakan peralatan ukur
elektronik seperti osciloskop dan spectrum analyzer. Peralatan tersebut
bekerja dengan memanfaatkan model matematik dari sinyal tersebut.
Pengolahan sinyal adalah suatu operasi matematik yang dilakukan
terhadap suatu sinyal sehingga diperoleh suatu informasi yang berguna.
Pengolahan sinyal dapat dilakukan secara analog atau digital. Pengolahan
sinyal analog memanfaatkan komponen-komponen analog, misalnya diode,
transistor, Op-amp, dan lainnya. Pengolahan secara digital menggunakan
komponen-komponen digital seperti register, counter, decoder, summing,
mikroprosesor, mikrokontroller, dan lainnya. Untuk kemudahan pada
pengolahan sinyal digital sebagai pemroses digunakan komputer
(mikrokontroller) untuk merepresentasikan algoritma atau model matematik.
1.3 Klasifikasi Sinyal
A. Sinyal Waktu Kontinyu dan Sinyal Waktu Diskrit
Sinyal x(t) disebut sinyal waktu kontinyu jika t adalah variabel
kontinyu. Jika t adalah variabel diskrit, maka x (t) didefinisikan sebagai sinyal
waktu diskrit. Sinyal waktu diskrit sering diidentifikasi sebagai urutan angka,
bab I - sinyal
2
dilambangkan dengan {xn} atau x[n], dimana n = bilangan bulat. Ilustrasi sinyal
waktu kontinyu x(t) dan sinyal waktu diskrit x[n] ditunjukkan pada Gambar. 11.
Gambar 1.3 a. Sinyal Waktu Kontinyu b. Sinyal Waktu Diskrit
Sinyal waktu diskrit adalah sinyal yang hanya ada pada waktu tertentu.
Misalnya kita mengukur suhu dalam suatu ruangan setiap satu menit, dengan
demikian kita tak dapat mengetahui suhu pada menit 1,5 menit. Setiap
komponen sinyal diskrit diberi nomor sesuai urutan pembacaan atau
pengambilan datanya. Jarak antar pembacaan ini disebut waktu sampling.
Sebutan diskrit dipergunakan untuk menunjukkan kondisi sumbu
waktunya. Artinya nomor komponen sinyal harus berupa bilangan bulat
sedangkan nilai dari sinyalnya berupa bilangan riil. Sebagai contoh, sebuah
sinyal diskrit x(m) memiliki komponen sinyal x(0), x(1), x(2), …… tetapi bukan
x(1,5) atau atau sesuatu yang semacam ini. Jadi nilai x(1,5) bisa dikatakan
tidak ada atau tidak terdefinisi. Konsep ini sangat penting untuk memahami
sinyal diskrit.
Sinyal waktu diskrit x[n] dapat diperoleh dari sampling sinyal waktu
kontinyu x(t) yaitu: x(to), x(t1), …, x(tn),
Sampling ke-(to), (t1), …, (tn) = nol dan bil. bulat positif, maka sinyal
waktu diskrit dapat ditulis:
x[0], x[1], …, x[n]
atau
Xn = x[n]=x(tn)
dengan x[n]= sinyal sampling dan tn = interval sampling
Jika interval sampling serbasama/uniform, maka:
Xn = x[n]=x(nTs)
dengan Ts= interval sampling
bab I - sinyal
3
Sinyal waktu diskrit x[n] dapat dinyatakan dengan dua cara:
1. Bentuk aturan tertentu dari urutan nilai ke-n. Contoh
1 𝑛
2
( )
𝑥[𝑛] = 𝑥𝑛 = {0
1 1
𝑛≥0
𝑛<0
1 𝑛
{𝑥𝑛 } = {1, , , … , ( ) }
2 4
2
atau
2. Bentuk eksplisit urutan nilai x[n]. Contoh:
{𝑥𝑛 } = {… , 0, 0, 1, 2, 1, 2, 2,0,0, … }
↑
tanda  menyatakan n=0, dan jika tidak terdapat tanda  maka n=0 pada data
pertama sedangkan untuk n<0 dianggap data=0
Jumlah dan perkalian sinyal waktu diskrit dinyatakan sbb:
{cn} = {an} +{bn}
 cn = an +bn
{cn} = {an}{bn}  cn = anbn
{cn} = {an}
 cn = an ,  = konstanta
Beberapa contoh sinyal diskrit adalah:
 Keluaran dari sebuah ADC
 Laporan jumlah produksi mesin tiap jamnya
 Catatan IHSG Byrsa Efek Jakarta per Minggu
 Catatan fluktuasi nilai tukar mata uang asing dalam satu tahun
Berikut contoh program MATLAB untuk menampilkan sinyal waktu
diskrit. Fungsi yang dipergunakan adalah stem
n = -5:1:5 % set untuk n dari -5 sampai 5 dengan jarak interval 1
x = [ 1 2 -5 3 -2 7 5 6 -1 5 -3];
stem(n,x,'linewidth',2);
bab I - sinyal
4
8
6
4
2
0
-2
-4
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
Gambar 1.4 Contoh Sinyal Diskrit
Sinyal waktu kontinyu menggunakan bilangan riil pada sumbu
waktunya. Karena menggunakan bilangan riil, maka kita bisa mendapatkan
nilai sinyal kapanpun. Hal ini tentu berbeda dengan sinyal waktu diskrit.
Sinyal waktu kontinyu dinyatakan dalam bentuk garis yang utuh, bukan
garis vertikal seperti sinyal diskrit. Penggunaan garis seperti ini menunjukkan
kita bisa mendapatkan nilai sinyal untuk setiap nilai waktu.
Berikut ini contoh menampilkan sinyal waktu kontinyu menggunakan
program MATLAB
t=0:0.01:8;
x=sin(2*pi*t/4);
plot(x,'linewidth',2)
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
100
200
300
400
500
600
700
800
900
Gambar 1.5 Contoh Siyal Kontinyu
Pada beberapa kasus, pengklasifikasian ini bisa membingungkan.
Sebagai contoh, untuk pengukuran suhu ruangan dengan nilai suhu
bab I - sinyal
5
bisa berupa bilangan riil. Apabila pencatatan dilakukan tiap 5 menit,
maka data yang didapatkan adalah sinyal diskrit. Tetapi saat
pembacaan dilakukan dengan menggunakan plotter seperti yang
dipergunakan untuk rekam jantung, maka kita mendapatkan sinyal
kontinyu. Jadi klasifikasi ini sangat tergantung dari cara mendapatkan
data yang diinginkan.
Beberapa contoh sinyal waktu kontinyu:
 Rekaman suara manusia di pita magnetik
 Pengukuran suhu ruangan yang tidak dilakukan secara
sampling
B. Sinyal Analog dan Sinyal Digital
Jika sinyal waktu kontinyu x(t) mempunyai nilai sembarang (bernilai
riil) pada interval waktu kontinyu (a,b) dengan a= -  dan b= , maka sinyal
waktu kontinyu x(t) disebut sinyal analog. Jika sinyal waktu diskrit x[n]
mempunyai nilai diskrit (bilangan bulat), maka sinyal waktu diskrit disebut
sinyal digital.
C. Sinyal Bilangan Nyata dan Sinyal Bilangan Kompleks
Sinyal x(t) disebut sinyal bilangan nyata jika nilai x(t) adalah nyata dan
x(t) disebut sinyal bilangan kompleks jika nilainya kompleks. Bentuk umum
fungsi sinyal bilangan kompleks atau sering disebut sinyal kompleks adalah:
x(t) = x1(t) + jx2(t), dengan x1(t), x2(t) = bilangan nyata dan j=-1
bab I - sinyal
6
bab I - sinyal
7
bab I - sinyal
8
1.4 Sinyal-sinyal Standar
Dalam analisis sistem, kita memerlukan beberapa sinyal standar untuk
memberikan hasil yang lebih akurat. Sinyal-sinyal ini terbagi atas sinyal diskrit
standar dan sinyal kontinyu standar
bab I - sinyal
9
Sinyal diskrit standar
Beberapa sinyal standar yang akan dibahas dalam buku ini adalah unit
step, unit impulse, unit ramp dan complex exponential.
Sinyal unit step adalah sinyal yang bernilai tetap, yaitu satu untuk
semua nilai waktu yang positif dan nol. Secara matematis, sinyal ini ditulis
sebagai:
1, untuk n ≥ 0
u(n) = {
0, untuk n < 0
Berikut, gambar yang menunjukkan sinyal unit step
Gambar 1.6 Sinyal unit step untuk sistem diskrit
Kita menggunakan sinyal ini untuk menunjukkan sinyal DC (bisa
tegangan maupun arus). Selain itu, kita bisa menggunakannya untuk
menunjukkan bahwa sebuah sinyal dimulai dari n = 0. Untuk menunjukkan hal
ini, sinyal tersebut harus dikalikan dengan sinyal unit step. Sebagai contoh,
sinyal y(n) akan dimulai dari n = 0, maka ditulis y(n) = u(n).sin(3n). Hal ini
bararti sinyal y(n) dimulai saat n = 0. Untuk n<0, y(n) tidak ada.
Sinyal unit impulse adalah sebuah sinyal yang bernilai satu pada saat n
= 0 dan untuk n selain nol nilainya nol. Sinyal ini ditulis sebagai (n) dan ini
dipakai sebagai notasi yang menunjukkan sinyal tersebut. Secara matematis,
sinyal ini ditulis sebagai:
1, untuk n=0
δ(n)= {
0, untuk n≠0
Berikut, gambar yang menunjukkan sinyal unit impulse
bab I - sinyal
10
Gambar 1.7 Sinyal unit impulse untuk sistem diskrit
Sinyal unit step dan unit impulse ternyata berhubungan satu sama lain. Hal ini
dapat ditunjukkan dengan persamaan berikut:
∞
𝑢(𝑛) = ∑ 𝛿(𝑛 − 𝑚)
𝑚=0
𝛿(𝑛) = 𝑢(𝑛) − 𝑢(𝑛 − 1)
Sinyal ramp adalah sinyal yang bernilai sama dengan waktunya, sinyal
ramp dinyatakan sebagai:
Ramp(n)=n, untuk n>=0
Gambar 1.8 Siyal Ramp untuk sistem diskrit
bab I - sinyal
11
bab I - sinyal
12
bab I - sinyal
13
bab I - sinyal
14
bab I - sinyal
15
bab I - sinyal
16
bab I - sinyal
17
bab I - sinyal
18
bab I - sinyal
19
bab I - sinyal
20
bab I - sinyal
21
bab I - sinyal
22
bab I - sinyal
23
bab I - sinyal
24
1.5 Representasi Sinyal
Sinyal dapat direpresentasikan dalam berbagai cara. Representasi sinyal
kontinyu dapat dijelaskan dengan lebih mudah dengan contoh berikut: Suatu
sinyal kontinyu seperti gambar berikut representasikan dalam suatu
persamaan isyarat:
x(t)
1
1
2
3
t
Gambar 1.8 Sinyal x(t)
Sinyal x(t) diatas mempunyai tiga kondisi yaitu: pada saat 0<t<2, pada saat
2<t<3 dan saat t yang lain. Dengan demikian dapat dirumuskan suatu fungsi
sebagai berikut:
x1(t), 0<t<2
x(t) =
x2(t), 2<t<3
x3(t), t lainnya
Dari grafik x(t) dapat dilihat bahwa kondisi selain 0<t<2 dan 2<t<3 tidak
ada sinyal x(t) atau dapat dituliskan x3(t) = 0. Sedangkan pada saat 2<t<3
terlihat bahwa sinyal x(t) bernilai 1 sehingga dapat dituliskan x2(t) = 1. Untuk
mencari nilai x1(t) dipergunakan rumusan persamaan garis antara dua titik.
Isyarat x1(t) melalu titik (0,0) yang selanjutnya disebut titik 1 dan titik (2,1)
yang selanjutnya disebut titik 2. Dengan dasar tersebut maka isyarat x1(t)
dapat dicari sebagai berikut:
x1 (t )  x1 t  t1

x 2  x1
t 2  t1
dengan memasukan nilai-nilai titik 1 dan titik 2 didapatkan:
x1 (t )  0 t  0

1 0
20
bab I - sinyal
25
maka:
x1 (t ) 
t
2
Jadi x(t) dapat ditulis menjadi persamaan berikut :
x(t) =
0,5t, 0<t<2
1, 2<t<3
0, t lainnya
Untuk menuliskan persamaan x(t) dalam satu persamaan dapat
digunakan u(t-a) dan u(t-b) sebagai awal dan akhir dari sinyal tersebut. Hal
tersebut dapat dipahami dengan ilustrasi sebagai berikut:
y(t)
1
a
b
t
(a)
y1(t)
y2(t)
1
1
a
(b)
b
t
a
b
t
(c)
Gambar 1.9 (a) Sinyal y(t), (b) sinyal y1= u(t-a), (c) sinyal y2=u(t-b)
Pada Gambar 1.9(a) adalah suatu sinyal yang bernilai 1 yang dimulai pada t = a
dan diakhiri pada t = b. Sinyal tersebut dari gambar dapat dilihat merupakan
hasil pengurangan sinyal y1(t) = u(t-a) (sinyal unit step yang tergeser ke kanan
sejauh a) dengan sinyal y2(t) = u(t-b) (sinyal unit step yang tergeser ke kanan
sejauh b).
y(t) = y1(t) – y2(t)
= u(t-a) –u(t-b)
bab I - sinyal
26
Sehingga representasi sinyal pada contoh soal di atas dalam satu persamaan
adalah:
x(t)
= 0,5t{u(t-0)-u(t-2)} + {u(t-2)-u(t-3)}
= 0,5t {u(t)-u(t-2)} + u(t)-u(t-3)
1.6 Operasi Dasar Sinyal
A. Atenuasi
Gambar Pelemahan Sinyal
Dalam bentuk pendekatan operasi matematika, peristiwa ini dapat diberikan
sebagai berikut:
h(t) =a x s(t)
Dalam hal ini nilai a<1, yang merupakan konstanta pelemahan yang terjadi.
Contoh:
Sebuah sinyal sinus s(t) = 2sin(2πfst) melalui suatu medium kanal yang bersifat
meredam dengan konstanta atenuasi 0,5. Berikan gambaran bentuk sinyal
sebelum dan sesudah melalui medium.
Penyelesaian:
Bentuk sinyal setelah melalui medium merupakan hasil kali sinyal masuk
dengan konstanta redaman yang dimiliki kanal yang dilaluinya. Dengan
memanfaatkan persamaan matematik di atas diperoleh bentuk sinyal
keluaran sebagai berikut so(t) = 0,5*s(t) = 0,5*2sin(2πfst) = sin(2πfst)
Gambar Pelemahan Sinyal Sinus
bab I - sinyal
27
B. Amplifikasi
Dalam bentuk penyederhanaan persamaan matematis, bentuk operasinya
sama dengan atenuasi, tetapi dalam hal ini konstanta a >1
Contoh:
Sebuah sinyal sinus s(t) = 2sin(2πfst) dikuatkan dengan sebuah suatu
rangkaian dengan gain 2x. Berikan gambaran bentuk sinyal sebelum dan
sesudah melewati rangkaian penguat.
Penyelesaian:
Bentuk sinyal setelah melalui rangkaian hasil kali sinyal masuk dengan gain.
Dengan memanfaatkan persamaan matematik di atas diperoleh bentuk sinyal
keluaran sebagai berikut so(t) = 2*s(t) = 2*2*sin(2πfst) = 4 sin(2πfst)
Gambar Amplifikasi sinyal Sinus
3. Pergeseran
Operasi pergeseran adalah operasi menggeser sinyal ke kanan atau ke kiri pada
sumbu waktu. Dalam aplikasi pengolahan sinyal, hal ini dilakukan dengan tunda
waktu.
pergeseran ke kanan : x(t-t0)
pergeseran ke kiri : x(t+t0)
Contoh soal 1.3:
bab I - sinyal
28
Lakukan Operasi pergeseran x(t-1) dan x(t+2) terhadap isyarat x(t) pada contoh soal
1.1.
x(t-1) dapat dicari sebagai berikut :
0,5(t-1),0<t-1<2
x(t-1) =
1,
2<t-1<3
0,
t-1 lainnya
dengan penyederhanaan:
x(t-1) =
0,5t-0,5,
1<t<3
1,
3<t<4
0,
t lainnya
Sedangkan x(t+2) dapat dicari sebagai berikut:
x(t+2) =
0,5(t+2),
0<t+2<2
1,
2<t+2<3
0,
t+2 lainnya
x(t+2) dapat disederhanakan:
x(t+2) =
0,5t+1,
-2<t<0
1,
0<t<1
0,
t lainnya
Sinyal x(t-1) dan x(t+2) dapat digambarkan sebagai berikut:
x(t-1)
bab I - sinyal
1
x(t+2)
1
29
Gambar 1.11 (a) Sinyal x(t-1), (b) Sinyal x(t+2)
Pada Gambar 1.11, terlihat operasi pergeseran sinyal. Sinyal x(t-1) adalah
sinyal x(t) yang tergeser 1 ke kanan. Sinyal x(t+2) adalah sinyal x(t) yang
tergeser ke kiri sejauh 2. Jadi pada isyarat dengan t mempunyai tanda
positif maka akan tergeser ke kanan sebesar suatu bilangan kalau di
kurangi suatu bilangan tersebut. Untuk pergesaran ke kiri (ditambah suatu
bilangan) juga demikian.
4. Penskalaan waktu
Penskalaan waktu adalah upaya menyempit dan melebarkan isyarat pada sumbu
waktu Contoh : Lakukan Penskalaan waktu x(2t) dan x(0.5t) terhadap isyarat x(t)
pada contoh soal 1.1.
a)
x(2t) dapat dicari dengan memasukan 2t untuk menggantikan t pada
fungsi x(t)
0,5t,
x(t) =
1,
0,
bab I - sinyal
0<t<2
2<t<3
t lainnya
30
Nilai t digantidengan 2t maka didapatkan:
x(2t) =
0,5.2t,
0<2t<2
1,
2<2t<3
0,
2t lainnya
Dengan menyederhanakan 2t maka didapat:
x(2t) =
t,
0<t<1
1,
1<t<1,5
0,
t lainnya
Sedangkan untuk x(0.5t) dapat dicari sebagai berikut:
x(0,5t) =
0,5(0,5t),
0<0,5t<2
1,
2<0,5t<3
0,
0,5t lainnya
Dengan penyederhanaan didapat:
0,25t ,
x(0,5t) = 1,
0<t<4
4<t<6
0,
t lainnya
x(2t)
x(0,5t)
1
1
bab I - sinyal
31
1
2
3
t
1
2
3
4
5
6
Gambar 1.10 (a) Sinyal x(2t), (b) Sinyal x(0,5t)
Pada Gambar 1.10, kalau dibandingkan dengan gambar sinyal x(t) terlihat jelas
operasi penskalaan waktu. Sinyal x(2t) merupakan operasi penyempitan skala
waktu setengah kali dari skala waktu asli. Sinyal x(0,5t) merupakan operasi
pelebaran skala waktu dua kali dari waktu aslinya.
5. Pencerminan
Operasi pencerminan dilakukan dengan mencerminkan isyarat terhadap sumbu
vertikalnya. Contoh : Lakukan Operasi pencerminan x(-t) dan x(-0,5t)
terhadap isyarat x(t) pada contoh soal 1.1.
a) Operasi pencerminan x(-t) dan x(-0,5t)
Nilai x(-t) dapat dicari sebagai berikut:
x(-t) =
-0,5t,
0<-t<2
1,
2<-t<3
0,
-t lainnya
dengan penyederhanaan didapatkan :
-0,5t,
bab I - sinyal
-2<t<0
32
x(-t) =
1,
-3<t<-2
0,
t lainnya
Sedangkan sinyal x(-0,5t) adalah sebagai berikut:
0,5(-0,5)t, 0<-0,5t<2
x(-0,5t) =
1,
2<-0,5t<3
0,
-0,5t lainnya
dengan penyederhanaan didapatkan :
x(-0,5t) =
-0,25t,
-4<t<0
1,
-6<t<-4
0,
t lainnya
Sinyal x(-t) dan x(-0,5t) dapat digambarkan sebagai berikut:
x(-t)
x(-0,5t)
1
-3
-2
1
-1
1
t
-6
-5
-4
(a)
-3
-2
-1
(b)
Gambar 1.12 (a) Sinyal x(-t), (b) Sinyal x(-0,5t)
bab I - sinyal
33
Pada Gambar 1.12, dapat dilihat bahwa sinyal x(-t) adalah hasil
pencerminan sinyal x(t). Sinyal x(-0,5t) adalah hasil pencerminan dan
penskalaan waktu sinyal aslinya.
Penjumlahan
Secara matematik dapat diberikan sebagai berikut:
g(t) = f(t) + h(t)
Contoh Penjumlahan Sinyal
Sinyal sinus f(t) = sin(4πfct) dijumlahkan dengan sinyal h(t) = sin(8πfct). Proses
penjumlahan dilakukan dengan menjumlahkan komponen sinyal f(t) dan
sinyal h(t) untuk setiap nilai t yang sama. Dalam matematis dituliskan
g(t) = f(t) + h(t)
= sin(4πfct) + sin(8πfct)
Perkalian
bab I - sinyal
34
Secara matematik dituliskan sebagai berikut:
g(t) = f(t) x h(t)
Dalam operasi matemati perkalian antar dua sinyal, setiap komponen ke-t
sinyal sinyal pertama dikalikan dengan komponen ke-t sinyal ke dua.
Contoh Perkalian Sinyal
Sebuah pemancar AM DSB-SC menggunakan operasi perkalian dalam proses
modulasi sinyal informasi si = 2 sin(2πfst) dan sinyal carrier sc = 4 sin (2πfct).
Nilai fs = 1 sedangkan fc=8. Bagaimana gambaran proses operasi perkalian
kedua sinyal diatas? Dan bagaiman bentuk sinyal akhir yang dihasilkan?
Penyelesaian:
Setiap komponen sinyal ss(t) dikalikan dengan komponen sinyal sc(t) untuk
setiap nilai t yang sama. Bentuk persamaan matematik dituliskan sebagai
berikut: s(t) = si (t) x sc (t) =2sin(2πfst) x 4sin (2πfct)
bab I - sinyal
35
Soal-soal untuk diselesaikan secara analitis
1. Beri gambaran sebuah sinyal waktu-kontinyu yang bersifat periodik
berupa sinyal sinus dengan frekuensi f = 5 Hz, dan fase awal θ = π/2
radiant.
2. Ulangi langkah tersebut untuk nilai f = 10 Hz, 20 Hz dan 30 Hz sementara
fase awalnya ditetapkan θ = 0 untuk semua kasus diatas.
3. Berikan persamaan untuk sinyal seperti Gambar berikut ini:
bab I - sinyal
36
Soal-soal untuk diselesaikan melalui Matlab
1. Bangkitkan sinyal sinus pada soal nomor 1 dengan menggunakan Matlab
untuk waktu dari t = 0 sampai t = 2 detik.
2. Bangkitkan sebuah sinyal sinus s1(t) = sin(8πfct) dan jumlahkan dengan
sebuah sinyal s2(t) = sin(5πfct + 0.5π). Berikan gambaran hasil
penjumlahan kedua sinyal tersebut.
3. Bangkitkan sebuah sinyal sinus s1(t) = sin(2πfst) dan kalikan dengan
sebuah sinyal s2(t) = sin(5πfct). Berikan gambaran hasil perkalian kedua
sinyal tersebut.
4. Sebuah kanal memiliki sifat melemahkan sinyal yang dilaluinya sehingga
menyebabkan level sinyal yang lewat turun 20%. Apabila sebuah sinyal
sinus memiliki persamaan s1(t) = sin(5πfct), dengan fc=10, maka beri
gambaran bentuk sinyal sebelum dan sesudah atenuasi.
bab I - sinyal
37
5. Sebuah sistem penguat memiliki gain 2,5x. Apabila sebuah sinyal sinus
memiliki persamaan s1(t) = sin(5πfct), bagaimanakah bentuk sinyal
sebelum dan sesudah amplifikasi terjadi?
bab I - sinyal
38