Pegas

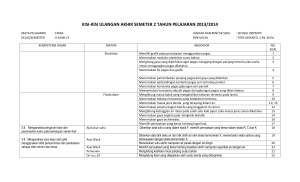
Konsep Dasar Getaran dan Gelombang
Kasus: Pegas
Powerpoint presentation by
Muchammad Chusnan Aprianto
Definisi
Gerak periodik adalah
gerakan maju dan mundur
atau melingkar pada
lintasan yang sama untuk
rentang waktu yang
seragam
Benda dikatakan bergetar
apabila benda tersebut
mengalami gerak periodik
Equilibrium position –
keadaan setimbang
Gaya luar F (tarik atau
tekan pada gambar b
dan c) bekerja pada
pegas dengan
mengakibatkan
peregangan sejauh x
Restoring Force, F = - k x
Gaya yang diberikan oleh pegas
Pegas menyimpan gaya
yang sama sebesar gaya
luar tersebut yang
berfungsi untuk gaya
pengembali ke keadaan
setimbang atau
restoring force
Dari urutan gambar di samping, gerak
osilasi terjadi pada sistem yang
selanjutnya bisa diturunkan beberapa
definisi
a. Displacement (perpindahan) adalah
jarak x dari benda yang bergetar dari
titik kesetimbangan
b. Amplitude (amplitudo) adalah jarak
maksimum yang benda bergetar dari
titik kesetimbangan
c. Cycle (siklus) adalah gerak benda dari
sembarang titik untuk maju dan
kembali mundur ke titik yang sama
d. Period (periode) adalah waktu ang
dibutuhkan untuk menyelesaikan satu
siklus
e. Frequency (frekuensi) adalah
banyaknya siklus yang bisa
diselesaikan dalam waktu satu detik
f = 1 / T ------> frekuensi, Hz atau s-1
T = 1 / f ------> periode, s
Pada keadaan setimbang, gambar a
adalah pegas pada kondisi
normal.
Pada gambar b, dengan
pembebanan massa m, pegas
meregang sejarak x0 dan
mengalami keadaan setimbang
(pada titik yang baru)
0 = m.g – kx0
m.g = kx0
x0 = (m.g) / k
Energi Potensial



Energi potensial pegas, didefinisikan sebagai
Pada pegas berputar (torsi) akan berlaku hubungan antara
momen M dengan pergeseran sudut , yang didefinisikan
sebagai
Sehingga energi potensial untuk pegas
Contoh

Nilai untuk sistem di samping m1 =
20 kg, m2 = 10 kg, Ip = 0.4 kgm2 , r =
10 cm, к = 1300 N/m.
 Tentukan energi potensial sistem
jika sistem dalam keadaan
seimbang!
 Cari bentuk energi potensial jika
pegas diputar sebesar  searah
jarum jam!
Solution

Dalam keadaan seimbang, perubahan yang terjadi
adalah pergeseran statik . Besarnya  adalah
Sehingga
Besarnya energi potensial dalam keadaan
setimbang adalah
Solution (Cont’d)

Pada saat berseger sebesar , akibatnya pegas mengalami
perubahan panjang
sehingga besar total perubahannya
Akibatnya bentuk persamaan energi potensial menjadi:
JENIS-JENIS PEGAS
Helical Coil (Pegas Berpilin)

Tipe pegas ini digunakan dalam aplikasi industi dan sistem
suspensi kendaraan.
Tipe ini terbuat dari batang yang berpilin dengan diameter D
dan modulus pergeseran G. Batang dibentuk menjadi N lilitan
dengan ruji r.

Torka maksimum pada tipe ini dirumuskan dengan

J adalah momen inertia kutub, yaitu

Helical Coil (Pegas Berpilin) (Cont’d)


Total perubahan panjang pegas akibat gaya tertentu
diprediksi sebagai
Konstanta pegas k dirumuskan dengan
Contoh


Sebuah pegas berpilin memiliki diameter batang 20 mm yang
terbuat dari 0,2% baja-C
. Diameter lilitan
20 cm, terdiri dari 30 lilitan.
 Berapakah gaya maksimal, sehingga besar pergeserannya
maksimalnya
!
 Berapakan perubahan panjang pegas ketika gaya maksimal
ini diterapkan!
Solution
 Tegangan maksmimal pegas adalah
Cont’d

Sehingga gaya maksimal yang diperbolehkan adalah

Besar konstanta gaya pegas adalah
Perubahan panjang akibat gaya maksimal:
Bahan Elastis sebagai Pegas



Penerapan gaya menyebabkan pergeseran (gambar di
bawah). Bahan elastis memiliki modulus E, panjang L dan
luasan A
Besar strain tali adalah
strain
dengan energi total
Gaya yang dibutuhkan untuk menghasilkan pergeseran x:
, sehingga nilai konstanta
Cont’d



Pada kasus terjadi momen
inertia I, maka besarnya
pergeseran
Sehingga
Pergeseran yang terjadi
periodik menyebabkan
getaran, jika w(z) adalah
fungsi pergeseran, maka
untuk z=a
dan
Cont’d

Untuk kasus bahan elastik yang diputar, maka momen gaya:

Shgg

G adalah modulus geser, J momen inertia kutub, dan I momen
inertia
Contoh


200 kg mesin dikaitkan pada penompang (bahan elastis)
dengan panjang L = 2,5 m, modulus elastisitas E = 200 x
109 N/ m2 , dan tampang lintang momen inertia I = 1,8 x 10−6
m4 . Dengan asumsi massa penompang lebih kecil daripada
massa mesin, berapa besar konstanta kekakuan k?
Solusi
 Untuk z=L dan untuk penompang berlaku

Besar konstanta k adalah
Jenis-Jenis Pegas Lainnya
Pegas Datar
Bentuk Khusus
Cont’d
Helical Coil Torsion
Bentuk Daun
Bahan Baku Pegas

Material yang digunakan dalam pembuatan pegas adalah
 Hard drawn high carbon steel
 Oil tempered high carbon steel
 Stainless steel
 Copper atau nickel based alloys
 Phosphor bronze
 Inconel
 Monel
 Titanium
 Chrome vanadium
 Chrome silicon
KOMBINASI PEGAS
Kombinasi Seri
Kombinasi Paralel (Pergeseran Simetri)
Kombinasi Paralel (Pergeseran Non-Simetri)
Kombinasi Seri-Paralel
SEKIAN