dispersi radioaktivita,s ke lingkungan tanah - ANSN

METODE
BEDA
HINGGA
DISPERSI RADIOAKTIVITA,S
PADA
KAJIAN
PEMODELAN
KE LINGKUNGAN TANAH
Supriyono
Pendidikan
Ah/i Teknik Nuk/ir-BATAN.
J/.Babarsari
Po. Box 1008 Yogyakarta
Sudarti
Pusa/ Pene/i/ian
Tekn%gi
Maju-BATAN.
JI.Babarsari
Po. Box 1008 Yogyakarta
ABSTRAK
METODE BEDA HINGGA PADA KAJIAN PEMODELAN DISPERSI RADIOAKTIVITAS
KE
UNGKUNGAN
TANAH. Telah dihasilkan persamaan matematis sebagai modal penyusunan
algoritma komputer yang berasal dari persamaan transpol1 yang merupakan bentuk dari konsep
dispersi radionuklida
di lingkungan tanah akibat proses difusi dan adveksi. Persamaan
matematis tersebut penurunannya
menggunakan metode beda hingga dengan tiga buah
skema, yaitu skema eksplisit, skema implisit dan skema Crank-Nicholson. Algoritma komputer
ini kelak akan digunakan sebagai dasar pembuatan perangkat lunak dalam rangka pembuatan
suatu sistem pemantauan dispersi radionuk/ida secara otomatis pads daerah sekitar fasilitas
nuklir.
Dengan
dipunyainya
ketigamendekati
skema tersebut,
kelak dalam memilih sistem perangkaf .
lunak dapat
memilih
yang paling
keadaanmaka
sebenamya.
ABSTRACT
FINITE DIFFERENCE
METHOD OF THE STUDY ON RADIOACTIVITIES
DISPERSION
MODELING IN ENVIRONMENT
OF GROUND. It has been resulted the mathematics equation
as model of constructing the computer algorithm deriving from the transport equation having
been the fonn of radionuclides dispersion in the environment of ground as a result of diffusion
and advection process. The derivation of mathematics equation used the finite difference
method into three schemes, the explicit scheme, implicit scheme and Crank-Nicholson scheme.
The computer algorithm then would be used as the basic of making the software in case of
making a monitoring system of automatic radionuclides dispersion on the area around the
nuclear facilities. By having the three schemes, so it would be, in choosing the software system,
able to choose the more approximate with the fact.
PENDAHULUAN
S eperti diketahui agar dipenuhi standar kesehatan
dan keamanan untuk lingkungan dan kesehatan
manusia, kadar radioaktivitas lingkungan disekitar
fasilitas nuklir harus selalu terpantau, baik dengan
dilakukannya pemeriksaan oleh petugas kesehatan
dan keselamatan kerja maupun melalui pantauan
inforrnasi secara otomatis. Inforrnasi tersebut salah
satunya adalah tentang keberadaan radionuklida
lingkungan
secara akurat yang merupakan
radionuklida yang berasal dari alam dan yang
berasal dari kegiatan manusia yang menggunakan
radionuklida. Seperti polutan lainnya, radionuklida
dapat pula menyebar ke lingkungan sekitar melalui
udara, tanah maupun air.
Untuk mendapatkan inforrnasi tersebut
secara otomatis, perlu dibuat suatu sistem
pemantauan dispersi radioaktivitas ke lingkungan
tanah. Pekerjaan pembuatan sistem otomatisasi
bukan pekerjaan yang mudah dan sederhana.
Pekerjaan ters~but adalah pekerjaan yang be~aryang
harus meialul proses pentahapan dan dldukung
dengan sumber daya manusia dari berrnacammacam disiplin ilmu misalnya, disiplin ilmu
elektronika, lingkungan. komputasi. matematika.
n.uklir, dsb. Sebagai tahap awal dari pembuatan
slstem tersebut adalah studi tentang dispersi
radionuklida ke lingkungan tanah beserta proses
penyelesaian matematis dan numeris.
Studi tersebut dimulai dengan melihat
persamaan diferensial
tentang
keseimbangan
transport massa. Persamaan tersebut menggunakan
konstanta fisis dari keadaan lingkungan daerah studi
yang dipakai. Persamaan diferensial dari transport
massa secara teoritis merupakan bentuk persamaan
diferensial parsial yang berbentuk parabola. Salah
satu cara untuk menyelesaikan secara numeris
persamaan diferensial parsial tersebut adalah
P3TM-BATAN Yogyakarta. 25-26 Juli 2000
I
dimana
i-l,1I
radionuklida
.
digunakannya
metode hecla hingga (Finite
Difference
Method)II.2]. Dengan diketahuinya
metode-metode tersebut, maka langkah berikutnya
adalah pembuatan algoritma sebagai langkah awal
dari pemrograman komputer.
Tulisan pada makalah ini adalah rnenyusun
bentuk persamaan matematis agar dapat diciptakan
algoritma pemrograman dari penggunaan metode
hecla hingga untuk
menyelesaikan persamaan
transport secara numeris beserta pencarian variabeJvariabel yang kelak akan digunakan dalam
pembuatan sistem pemantauan dispersi radionuklida
secara otomatis.
DASAR
berpasir
ataupun tanah
Seperti telah diketahui bersama bahwa
potensi bahaya terutama untuk radionuklida umur
panjang dapat berasal dari rantai makanan melalui
jalan pemafasan clan pencemaan. Dalam kaitan
dengan rantai makanan, faktor pencemaran
radionuklida dalam tanah di sekitar fasilitas nuklir
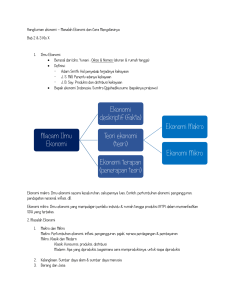
perlu diperhitungkan. Radionuklida yang mungkin
terdeposisi dalam tanah sekitar fasilitas, terutama
pada daerah perakaran akan dapat berlanjut masuk
ke rantai makanan melalui rantai seperti gambar I
atau
a. Bentuk skema eksplisit.
Pada skema eksplisit, variabel pada waktu
n+ J dihitung berdasarkan variabel pada waktu n
yang sudah diketahui seperti pada gambar berikut :
i,n+1
.o
1
~---1I,n
..
I- ,n
Q1+1,n
Dengan menggunakan skema seperti pada
gambar 2, beserta turunannya dalam ruang dan
waktu didekati dengan bentuk beda hingga berikut :
q(X,t)::::q~1
( )
berikut :
Fall 001dalam bemlJ<
Fall out dalam ber1~
1
aerosollerlarlA
RadlonlA<lldayang dapat
IIda~)
RadiO~idayangtidakl..J
dlserap}~!:I1buhan
H
dlseraptu~~
radortlklda dari
produk~1
Radionuklida
yang
L~tan
Tanah
n
-qi
6.t{)q(x~t2
(2)
= .9cl.:-9l:J.
26.x
n
2
n
0
qj +qj+1
= qi-l- 6.x2
/).t adalah perubahan waktu clan L1xadalahperubahanjarak
Bentuk skema implisit.
Pada skema implisit mas kanan dari
persamaan (1) ditulis pada waktu n+ 1 yang nilainya
belum diketahui. Gambar berikut menunjukkan
jaringan bentuk implisit.
U
H
A
N
bermg~si
Gambar1. Rantai radionuklida dari produk fisi
sampaike tumbuhan
Konsep dasar dispersi radionuklida di
lingkungan tanah adalah karena terjadinya proses
difusi dan adveksi yan~ dinyatakan dengan
persamaan transport berikuf ]:
'(x,t)~-
qj
at
[. ~~
T
U
n+1
~t~=
{}2q(;
=0
berlumut
Gambar2. BentukSkemaEksp/isit
TEORI
p~kel d~1produk~
yang
berumput.
Ada tiga skema dasar untuk menyelesaikan
persamaan parabola (I), yaitu skema el,<splisit,
skema implisit clan skema crank-NichoISOnl4)
"
)
i-l,n+l
i,n+l
l+l,n+l
-,
i,n
i+l,n
Gambar3. BentukSkemalmpisit
Denganmenggunakanskema seperti gambar 3, q(x,t) besertaturunannya dalam ruang dan
waktu didekatidenganbentukbedahingga berikut :
at
dimana
dalam tanah
q(x,t) : Konsentrasi
(Bq/L).
D(x,t) : Koefisien dispersi (cm1/tahun).
co
: Kecepatan dispersi dalam tanah (cmltahun).
A
: Konstanta peluruhan radioaktif (per detik).
D clan v bergantung pada macam tanah, nilai
tersebut akan berbeda untuk tanah berlempung,
q(x, t) = q~+1
..I
_.1
-
(3)
c. BentukskemaCrank-Nicholson.
Skema Crank-Nicholsonini menggunakan
paduan antara bentuk skema eksplisit daD bentuk
skema implisit, sehingga skema Crank-Nicholson
menulis ruaskananpersamaan(1) padawaktun+ 1/2
yang merupakannilai reratadari skemaeksplisitdaD
implisit. Jaringan bentuk skema Crank-Nicholson
adalahsebagaiberikut
i-l,n+l
i +l,n +1
i,n+l
matematis yang berasal dari ketiga skema di atas,
yang nantinya dipilih untuk dipakai yang paling
sesuai dengan kondisi di lapangan. Oleh karena itu,
sebelum dilakukan proses penyusunan algoritma
dan pemrograman komputer pacta penelitian
mendatang, perlu dilakukan
langkah-langkah
penyelesaian matematis sebagai berikut :
I. Bentuk persamaan matematis dari skema
eksplisit.
Substitusikan persamaan (2) kedalam persamaan
(I), maka :
~n+l/2
9i "+1"-qi
["
tlt
i9,n
~,n
i+J:n
= D(x, t
{
"
2"
qj-1 -qj
"
+ qi+\
6,x2
"
(j)~
~
(5)
-i.,q(x,t)
Gambar4. Ben/ukSkemaCrank-Nicholson
Dengan menggunakan skema seperti pada
gambar 4, q(x,t) beserta turunannya dalam rnang
dan waktu didekati dengan bentuk beda hingga
berikut :
q(x,t)=
( )
M
~
n+1
= 9i
-qi
n+1
I~-
Ox
2
persamaan
".,
"+1
clan q(x,t)=q"i
(5)
menjadi
I
"
.
Dengan
n+\
~=qi+l-qi-1
(
D(x,t)=D"j
iterasi,
n
~t
( )
n+\
mengelompokkan
suku-suku
q~.1.q~ .q~1 seperti pada bentuk skema gambar 2,
2~x
1 n+1 2
-qj
02q(X,t) = -qi-1
bentuk
proses
q~+1
at
M
Dengan merubah
kebentuk
bentuk
n+\
n
2
+ qi+1 + qj-l-
~X2
n
n'
qj + qi+\
maka persamaan akhir
dengan skema eksplisit
adalah:
~x2
(4)
Dari ketiga bentuk skema di atas beserta
persamaannya, makajika persamaan (2), (3) dan (4)
disubstitusikan ke dalam persamaan (1) akan
dihasilkan suatu bentuk sistem persamaan biasa
maupun bentuk bentuk sistem persamaanlinier.
PENYELESAIAN
Dengan
persamaan
tentang
(1)
menggunakan
dapat
syarat
diperlukan.
persamaan
MATEMATIS
ketiga
dieliminir
awal
dan
dan
skema
dapat
syarat
Dengan
dihasilkannya
dalam
bentuk
iterasi
beserta
syarat-syarat
disusun
algoritma
yang
batas
yang
maka
pembuatan
dapat
program
komputer.
Dalam makalah
ini hanya dibatasi pada
bentuk
persamaan
matematis
dan khusus
untuk
metode
eksplisit
algoritma.
penelaahan
diperlukan
Selain
dilengkapi
hal
dengan
bentuk
dapat
disusun
tersebut,
ukuran-ukuran
serta
persyaratan
DO n=OTO k
DOi=1TOI
q(n+1,i)=(D(n,i)*(dVdx)-(1/2)*omg)*q(n,i-1
)+
penyelesaian
yang
lengkap
diperlukan,
untuk
diatas,
diselidiki
besaran
fisis
penyelesaian
yang
iterasi
(1-2*D(n,i)*(dVdx"2)-Lamd)q(n,i)+
(D(n,i)*(dVdx"2)-(1/2)*omg*(
dVdx))q(n,i+1)
ENDDO
ENDJ;!9
~-
Algorimat J. Skema Eksplisit
Jika n=O, maka
q(O,i-J), q(O,i) dan q(O,i+ J)
merupakan nilai awal yang harus ditetapkan sejak
awal. Nilai ini merupakan ni!ai observasi dari obyek
penelitian di lapangan.
lainnya.
yang
Agar dihasilkan algoritma pemrograman
optimal, maka perlu disusun persamaan
~Prosiding
Pertemuan dan Presentasi Ilmiah Penelitian Dasar Ilmu Pengetahuan dan Teknologi Ni:Jklir
P3TM.BATAN Yogyakarta. 25-26 Juli 2000
skema
~
ISSN0216-3128
Supriyono.dkk
2. Bentuk
Implisit. persamaan matematis
dari
~'~
Substitusikan persamaan (3) kedalam persamaan
(I),
maka:
..
q~+1 -q!'
L\t
(x,t
=0
{
..; -t~,~i~
qj.1
n+1 -2q~+I+
315
q ~+Iq'=-D(X,tXq'-1
~ 1
I
~+I- 2 q I~+1+
At
2
Ax2
0
2 0
0
0+1
0-1
qj-1 -~i2 + qi+l] -C1) ~i!:l_:gj-1
q 1+1+
~+1
[
q 1+1
~+1
(9)
I
2L\x
I
I q~+1-n-!
1+1
Dengan
L\x2
(7)
qj-1
merubah
Oengan merubah bentuk O(x, t) = or
dan
q(x, t) = q~ kebentuk proses iterasi, persamaan (7)
(
" ,
.~J
6.t "
q ~+1 = q ~+ lDn .
I
I 2 i ..2
'
-
n+1 + qi-\
n + qi+\
6.x
suku-suku
.
,qj+1 sepertl pada bentuk serna
k
gambar 4,
qj-1 ,qj
maka persamaan akhir dengan skema CrankNicholson adalah :
mengelompokkan
n+1 n+1 n+1
q!I
mengelompokkan
n+1 n+1 n+1
Oengan
I-I
(-6.t
2qin +qi+J--O)
n
1
Dengan
l
{ q ?+1 -2
ux
2
!:!.tJf n+1
n+l )
n
2(1) ~ \qj+1-qj-1 -Aqj
I
dan
q(x, t) = q~ kebentuk proses iterasi, persamaan (9)
menjadi bentuk
-,
D(x, t) = Dr
menjadi bentuk
2L1x
q~+I,--
bentuk
suku-suku
.
qi-1 ,qj ,qj+\ sepertlpad a bentukskemagambar3,
makapersamaanakhir denganskemaimplisit adalah
)
(~
6.x
_l
120)
2..Dn
I
(~ 2 })qw!,+I + (I+D. (~ 2 )+/1.,,)q.!,+l
!1
6.x
6.x
(~ ) _lDn2 i (~6.x2))qj+ln+I= (!D!1
(~ )) !1 +
2 I 6.x2 q,+1
+ '!O)
2
6.x
(~(I)(*)-or(-!jr
+ ( ~(I)(*
))qi.tl+(
)-or( -!jr)
1+20r(-!jr
)qr+il = q~
)+A)qr+1
(8)
(~ ))q!,.2.+ (lD~(~6.x2 ))q!'-I 1
Persamaan (10) di atas jika
Persamaan
(8)
di
(~~~}Dr(-!;r
))=1'
(1+2Dr(~ )+>.)= b
(H~}q{~)r
atas
misalkan
dan
jika disusundengan;=1 sampai
j, maka persamaan(8) akanberubahmenjadibentuk
sistempersamaanlinier berikut:
n+1
bcO
O q~+1
abc
Gab
O q2
...:::::.
0
OOO b
n+1
q3
~+I
n
a
n+1
q\ -n qo
q2
-n
-q3
n'
n+1
qj
qj -cqj
, sehinggaada suatuprosesmanipulasimatrik dan
ada prosesGaussian.Algoritma denganmanipulasi
matrik dan proses Gaussianakan dibahas pada
penelitiankami berikutnya.
Bentuk persamaanmatematisdari skema CrankNicholson
Substitusikan persamaan (4) kedalam
persamaan(1), maka:
(10)
'1-2D!1
,
.6.x2
dengan i=l
dijalankan
sampai j temyata juga merupakan
bentuk sistem persamaan linier seperti halnya pacta
skema implisit, sehingga seperti pactaskema implisit
di atas proses skema Crank-Nicholson juga acta
suatu proses manipulasi matrik dan proses Gaussian.
Algoritma proses skema Crank-Nicholson akan
dibahas pactapenelitian kami berikutnya.
HASIL
DAN
PEMBAHASAN
Dari ketiga bentuk penurunan matematis di
atas,maka dapat dianalisis tentang variabel-variabel
clan konstanta-konstanta yang diperlukan. Untuk
membahas hal tersebut, dalam makalah ini dibahas
pada masing-masing skema.
Skema eksplisit.
Dari persamaan (6) ada beberapa besaran
yang harus ditentukan sebelum dilakukannya proses
iterasi, yaitu :
a. Dj merupakan koefisien dispersi pada seluruh
bidang penelitian (cm2Itahun), (J) adalah
kecepatan dispersi dalam tanah (cmltahun) dan
)., adalah konstanta peluruhan radioaktif (per
detifc). Data tersebut merupakan data sekunder
Prosiding Pertemuan dan Presentasi Ilmiah Penelitian Dasar Ilmu ?engetahuan
P3TM-BATAN Yogyakarta, 25-26 Juli 2000
dan Teknologi Nuklir
.,
1
yang berasal dari pihak lain, sehingga faktor
kerjasama dengan pihak lain perlu sekali.
b. L\t sebagai konstanta yang ditentukan sejak awal
merupakan nilai yang agak tleksibel. Nilai ini
merupakan
besaran
perubahan
waktu
yang
besamya tergantung dari konstanta di atas. L\x
sebagai konstanta perubahanjarak juga demikian
halnya, yaitu bergantung dari domain obyek
penelitian. Dipandang dari disiplin ilmu analisis
numerik, perlu ada kehati-hatian dalam
menentukan
L\t
dan
L\x.
Karena
faktor
ini
menentukan akurasi hasil perhitungan, stabilitas
komputasi dan besaran memori komputer yang
diperlukan dalam proses otomatisasi sistem
informasi kelak, Logika penentuan L\t dan
L\x.adalah menentukan nilai sekecil mungkin,
tetapi tidak sampai pad a angka batas stabilitas,
Tentang angka stabilitas akan disampaikan pada
makalah lain, Perhitungan batas stabilitas
memerlukan pengkajian yang mendalam dan
bersifat khusus, karena diperlukan penurunan
rumus-rumus matematika yang rumit dan agak
teoritis.
c, Harga awal (initial value) merupakan nilai yang
ditentukan sejak awal berdasarkan proses iterasi,
Adapun
harga
awal
muncul
akibat
diidentifikasi. Atau sebaliknya, untuk perhitungan
iterasi konsentrasi radionuklida dalam tanah pada
daerah seperti gambar 5, nilai-nilai konsentrasi
radionuklida dalam tanah mana saja yang sejak awal
harus disediakan sebagui nilai awal dan syarat batas.
Skema implisit.
Untuk pembahasan skcma ini, titik
tolaknya adaJahpersamaan (8). Nilai-nilai konstanta
Dr. (J) dan A.mcrupakan konstanta awal yang
harus tersedia seperti halnya pada pembahasan
skema eksplisit. Sedangkan perubahan jarak Llx
dan perubahan waktu ~t .dapat ditentukan sejak
awal. Hanya saja secara teoritis ads perbedaan
teknik penentuan nilai ~t dan Llx .antara skema
eksplisit dan skema implisit. Dari persamaan (8),
penentuan nilai awal dan syarat batas mempunyai
bentuk domain sebagai berikut :
"q,
""
~c""--oj~
/
'V
"",q'i
'-4.
proses
berikut. Pada saat 11=0, nampak bahwa pada
persamaan (6) ada nilai
q.,
~
y
C-
cj/
--xr"
q~.I,q~,q~+I' yang
diperlukan agar muncul nilai q:, Sedangkan
untuk iterasi berikutnya, misalnya n= 1, hasilnya
adalah q~ dengan syarat batas yang harus
d' b .k
. k
I
'
0
I
2
n
I erl an seJa awa, yaltu qo,qo,qo,...",qo dan
q0 , I
d .(' ) d
2
I
Imana m -max I
an
m q m , q m ,.,.." q m
l=max(t), Daerah harga awal dan syarat batas
untuk langkah iterasi skema eksplisit adalah :
Skema Crank-Nicholson.
Seperti
skema
halnya
dasar pijakan
setelah
mirip
sehingga
semua
sekali
proses
domainnyapun
sedikit
Nicholson
lebih
skema
persamaan
penentuan
awal
daTi pada
Sehingga
radionuklida
i1nplisit,
niiai-nilai
skema
bentuk
skema
eksplisit
akurasi
daerah
dalam
~t
maupun
perhitungan
penelitian
akan lebih bagus.
~-~-
ada
Crankkesalahan
pad a suku
pada
batasnya
sarna. Hanya
~x tertentu
error)
dalam
tersebut
temyata
Bahkan
dalam
jarak
untuk
menjadi
dan syarat
implisit.
yaitu
(truncation
implisit.
konsentrasi
dengan
dapat dikatakan
ini perubahan
kecil
(10)
seksama
skema
perbedaan,
pemotongan
Persamaan
dengan
nilai
pada
di atas,
(10)
proses
konstanta-konstanta,
skema
ini persamaan
pembahasan.
diperhatikan
bentuknya
seperti
kedua
Crank-Nicholson
--
Prosiding Pertemuan dan Presentasi IImiah Penelitian Dasar IImu Pengetahuan dan Teknologi Nuklir
P3Tr~.BATAN YoQvakarta. 25-26 Juli 2000
Supriyono. dkk
ISSN0216-3128
Setelah berhasil mengidentifikasi nilai-nilai
konstanta, nilai awal dan syarat batas dari ketiga
skema diatas, maka langkah berikutnya adalah
menyusun algoritma dan pembuatan program
komputer, agar dihasilkan nilai konsentrasi
radionuklida dalam tanah secara otomatis dengan
modalnya adalah persamaan(6), (8)dan (10).
KESIMPULAN
I.
Dengan menggunakan metode beda hingga,
maka dapat dihasilkan persamaanmatematis dari
skema eksplisit, implisit dan Crank-Nicholson
guna dijadikan modal dasar penyusunan
algoritma pemrograman komputer dalam rangka
pembuatan otomatisasi sistem pemantauan
konsentrasi radionuklida ke lingkungan tanah.
2. Dari ketiga skema tersebut temyata masingmasing mempunyai kelebihan dan kekuarangan,
misalnya jika
ditinjau
dari kemudahan
pembuatan algoritma pemrograman komputer
nampak bahwa skema eksplisit lebih mudah
dibanding dengan skema implisit maupun skema
Crank-Nicholson. Karena skema eksplisit tidak
memerlukan proSes manipulasi matriks maupun
proses Gaussian. Tetapi jika yang dilihat adalah
fleksibelitas nilai awal dan syarat batas, skema
implisit dan skema Crank-Nicholson lebih luwes
dibandingkan dengan skema eksplisit. Sehingga
dalam aplikasi kelak daerah pengamatan
konsentrasi radionuklida dalam tanah lebih dapat
memilih seperti keadaan yang sebenamya.3.
Akibat adanya keterbatasan dari masing-masing
skema, maka tersedianya data-data awal. sistem
perangkat keras dan bentuk daerah pengamatan
akan mempengaruhi pengambilan keputusan
tentang skema apa yang akan digunakan.
PENUTUP
Kerumitan dan keakurasian persamaan
matematis beserta algoritma pemrograman komputer dan sistem perangkat lunak kelak, tidak akan ada
manfaatnya jika tidak tersedia data-data nuklir
seperti yang diharapkan dalam tulisan ini. Oleh
karena itu pintu kerjasama kepada semua pihak
yang mempunyai data nuklir tersebut dibuka lebarlebar, agar terciptanya suatu sistem pemantauan
dispersi radionuklida
secara otomatis yang
bermanfaat bagi kesehatan dan keamanan untuk
lingkungan dan manusia di sekitar fasilitas nuklir.
DAFTAR
PUS TAKA
I. CHAPRA,S.C;
CANALE,R.P.,
Methods
For
Engineers",
Company Singapore, 1989.
"Numcrical
McGraw-HilI
317
2. SEWELL,G., "The Numerical Solution Of
Ordinary And Partial Differential Equations",
Academic PressInc London, 1988.
3. BELLI,M.; TIKHOMIROV,F.,
"Behavior Of
Radionuclides In Natural And Semi-Natural
Environments",
International
SQientific
Collaboration On The Consequences Of The
Chernobyl Accident (1991-1995), ECSC-ECEAEC, Brussels, Luxembourg, 1996.
4. TRIA TMODJO,B.; "Metode Numerik", Beta
Offset Y ogyakarta, 1995.
5. AXELSSON,O.
;
BARKER,V.A,
"Finite
Element Solution of Boundary Value Problems",
Academic Press,Inc, London, 1984.
6. SINCERO,A.P.; SINCERO,G.A.,
"Environmental Engineering", Prentice Hall, New Jersey,
1996.
TANYA
JAWAB
Sudarmadji
)- Dari ketiga skema ini ma_nayang terbaik ?
Suprlyono
-9- Dari ketiga skema,yaitu skema eksplisit,
implisit don Crank-Nicholson,untuk..L1tdon
Ax yang lebih kecil, skemaCrank-Nicholson
lebih bait Tetapidalampemilihan skemaini
tergantungdari persoalannya.
Tono Wibowo
)- Bagaimana langkah-langkah metode
hingga pada penelitian saudara ?
beda
Suprlyono
-9- Menentukanskema(eksplisit,implisit, cranknicholson),menurunkanskematersebutpada
persamaan awal menjadi persamaan
matematis,menentukannilai awal (IVP),
menentukansyarat balas, perhitungan don
komputasi.
Sahat Simbolon
)- Bagaimana dapat dibuktikan bahwa salah satu
dari persamaanmatematis di atas paling baik ?
Supriyono
-9- Vntuk membuktikan skema mana yang
terbaik, skemaeksplisit, implisit don cranknicholson mempunyaikarakteristik sendirisendiri. Oleh karena itu dalam pemilihan
skema tergantung dari persoalan masingma.\'ing(caseby ca.\'e)
Prosiding Per1emuan dan Presentasi IImiah Penelitian Dasar IImu Pengetahuan dan Teknologi Nuklir
P3TM-BATAN Yogyakar1a. 25-26 Juli 2000