Listrik Statik: Muatan, Gaya, Medan

Listrik Statik: Muatan, Gaya, Medan
Agus Suroso
Fisika Teoretik Energi Tinggi dan Instrumentasi, Institut Teknologi Bandung
Pekan #1
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
1 / 19
Muatan Listrik (q)
Ada dua macam: positif dan negatif.
Sejenis tolak menolak, beda jenis tarik menarik.
Muatan fundamental e = 1, 602 × 10−19 Coulomb.
Atau, 1 C = 6,25×1018 e.
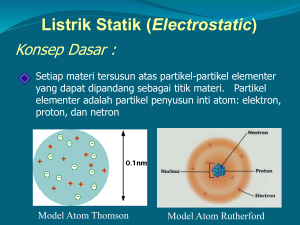
Atom = proton + neutron + elektron.
|
{z
}
inti
Partikel
Proton (p)
Neutron (n)
Elektron (e)
Muatan listrik
Agus Suroso (FTETI-ITB)
Massa (kg)
Muatan
−27
1,673×10
+e
1,675×10−27 0
9,11×10−31
-e
terkuantisasi dan terkonservasi.
Listrik Statik
Pekan #1
2 / 19
Gejala Listrik Statik
Contoh: interaksi antara balon dengan sweater dan tembok (simulasi:
https://phet.colorado.edu/en/simulation/balloons-and-staticelectricity).
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
3 / 19
Gaya Coulomb
Besarnya interaksi antara dua partikel bermuatan (masing-masing q1
dan q2 ) adalah
q1 q2
(1)
F~12 = k 2 rˆ12 ,
r12
1
dengan k = 4πε
= 9 × 109 Nm2 /C2 , dan ~r12 = ~r1 − ~r2 adalah posisi
0
relatif kedua partikel.
q1
r2 ­ r1
q2
r1
r2
O
F12 : gaya pada q1 akibat q2 . Dengan prinsip aksi-reaksi, F21 = −F12 .
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
4 / 19
Gaya Coulomb
Soal
1
Bandingkan besar gaya Coulomb dan gaya gravitasi antara dua
elektron yang terpisah sejauh 1 m. (Petunjuk: gaya gravitasi antara
dua benda m1 dan m2 yang terpisah sejauh r adalah F = − Gmr12m2 ,
dengan G = 6, 67 × 10−11 Nm2 /kg2 .)
2
Menurut model Bohr, atom Hidrogen terdiri atas satu proton yang
dikelilingi oleh satu elektron dengan jejari orbit 5, 35 × 10−11 m.
Dengan menganggap gaya Coulomb sebagai gaya sentripetal,
tentukan kecepatan sudut dan kecepatan tangensial elektron dalam
atom Hidrogen.
3
Suatu 4ABC sama sisi terletak pada kuadran I koordinat Kartesius.
Pada titik A (0,0) dan B (2,0) terdapat partikel bermuatan
qA = 1 µC dan qB = 2 µC. Berapakah besarnya gaya Coulomb yang
dialami oleh partikel di titik C yang bermuatan qC = 3 µC akibat dua
partikel yang lainnya? Tentukan pula arahnya.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
5 / 19
Gaya Coulomb
Soal
4. Suatu partikel bermuatan q1 = +8q terletak pada titik x = 0 dan
partikel lainnya bermuatan q2 = −2q terletak pada x = L. Pada titik
manakah sebuah proton harus diletakkan agar ia dalam keadaan
setimbang (ΣF = 0)? Apakah kesetimbangan tersebut stabil?
5. Titik pusat dua bola konduktor identik A dan B terpisah sejauh a
(yang nilainya jauh lebih besar dibanding jejari bola). Bola A
bermuatan +Q sedangkan B netral. Kedua bola kemudian
dihubungkan oleh kawat konduktor yang tipis. Berapakah besar gaya
listrik antarbola jika kawat dihilangkan?
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
6 / 19
Medan Listrik
Suatu partikel (misal A) bermuatan menimbulkan medan listrik di
daerah di sekitarnya.
Jika partikel lain (B) diletakkan di sekitar A, maka B akan
berinteraksi dengan medan yang ditimbulkan oleh A. Sehingga B
mengalami gaya listrik.
Besarnya medan listrik di titik P sejauh r dari partikel bermuatan q
adalah
kq
E~ = 2 rˆ,
(2)
r
dengan rˆ adalah vektor satuan yang arahnya dari partikel ke titik P.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
7 / 19
Medan Listrik oleh Partikel Titik
Mengacu pada persamaan (2), arah medan akibat partikel bermuatan
positif adalah menjauhi partikel, sebaliknya medan akibat muatan
negatif adalah menuju partikel.
Simulasi: https:
//phet.colorado.edu/en/simulation/charges-and-fields
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
8 / 19
Medan Listrik oleh Partikel Titik
Soal
1
Partikel A (qA = 4 µC) dan B (qB = −3 µC) terpisah sejauh 1 m. Di
titik manakah di sekitar kedua partikel yang medan listriknya nol?
2
Pada tiap sudut 4ABC yang memiliki panjang sisi 2 m terdapat
partikel bermuatan (masing-masing) qA = 2qB = −3qC = 6 µC.
Tentukanlah besar dan arah medan listrik di titik pusat segitiga.
3
Suatu dipol listrik tersusun atas satu muatan positif (+q) dan satu
muatan negatif (−q) yang terpisah sejauh d. Tentukan besarnya
medan di titik P yang berjarak z >> d dari titik tengah dipol dan
terletak pada sumbu dipol.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
9 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Teknik Dasar dalam Penyelesaian Soal
1 Tentukan satu partisi muatan dq dan tuliskan medan yang
ditimbulkannya,
kdq
d E~ = 2 rˆ,
(3)
r
dengan r adalah vektor yang menghubungkan posisi partisi dq dengan
titik diukurnya medan.
~ menjadi komponen-komponennya, misal
2 Uraikan vektor d E
ˆ
d E~ = dEx iˆ + dEy j.
3
(4)
Integralkan tiap komponen untuk mendapatkan medan total
Z
ˆ
d E~ = dEx iˆ + dEy jˆ ⇒ E~ = Ex iˆ + Ey j.
(5)
Perhatikan juga aspek simetri benda, kadang ia mempermudah proses
perhitungan.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
10 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 1: Medan listrik akibat batang-lurus yang bermuatan.
Jika muatan tersebar merata, maka λ ≡
dq
dx
konstan.
Medan di P akibat satu bagian kecil bermuatan dq = λdx adalah
dE = k
Medan akibat muatan total
Z
E=
dq
λdx
=k 2 ,
2
x
x
l+a
dE =
a
Agus Suroso (FTETI-ITB)
Listrik Statik
(6)
kQ
.
a (l + a)
(7)
Pekan #1
11 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 2: Medan listrik akibat batang-lurus yang bermuatan.
Berapa medan total di P?
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
12 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cincin tipis yang bermuatan.
Dari simetri, terlihat bahwa medan di P akibat partisi 1 dan 2 yang
berarah tegaklurus sumbu cincin saling meniadakan, sehingga yang
tersisa hanya medan arah sumbu-x.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
13 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cincin tipis yang bermuatan.
Medan akibat partisi 1, yang bermuatan dq adalah
dE = dEx =
Agus Suroso (FTETI-ITB)
kdq
kdq
x
√
cos θ = 2
.
2
2
2
r
(a + x ) a + x 2
Listrik Statik
Pekan #1
(8)
14 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cincin tipis yang bermuatan.
Medan total di P adalah
Z
E=
Agus Suroso (FTETI-ITB)
dE =
kxQ
(a2 + x 2 )3/2
Listrik Statik
.
(9)
Pekan #1
15 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cakram bermuatan.
Cakram sama dengan kumpulan cincin dengan jejari berbeda yang disusun
sepusat.
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
16 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cakram bermuatan.
Perhatikan cincin berjejari r dan bermuatan dq = σ2πrdr . Berdasarkan
hasil sebelumnya, cincin tsb menimbulkan medan sebesar
dE =
Agus Suroso (FTETI-ITB)
k2πrdr
(10)
(r 2 + x 2 )3/2
Listrik Statik
Pekan #1
17 / 19
Medan Listrik oleh Muatan Terdistribusi Kontinyu
Contoh 3: Medan listrik akibat cakram bermuatan.
Jadi, medan total yang ditimbulkan cakram adalah
d (r 2 )
Z
E=
R
Z
dE =
0
Agus Suroso (FTETI-ITB)
0
R
z}|{
k2π rdr
(r 2 + x 2 )3/2
"
= 2πkσ 1 −
Listrik Statik
#
x
(R 2 + x 2 )1/2
Pekan #1
(11)
18 / 19
Ada pertanyaan?
Agus Suroso (FTETI-ITB)
Listrik Statik
Pekan #1
19 / 19