- muhammad zainul arifin

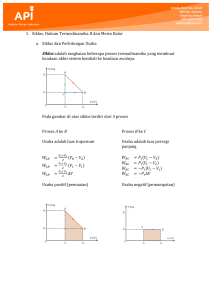
REVERSIBLE, IRREVERSIBLE
Sebelum membahas apa itu siklus carnot, pertama-tama kita harus
memahami yang disebut dengan proses terbalikkan (reversible) dan tak
terbalikkan (Irreversible). Proses reversible adalah proses dimana tidak ada energi
yang terbuang dari sistem tersebut, contoh dari proses reversible ini, misalkan kita
mempunyai bola yang kita pegang di atas gedung yang tingginya 10 meter, yang
artinya bola itu memiliki energi potensial tertentu, kemudian bola itu kita lepaskan
dari ketinggian tersebut dan jatuh ke lantai, karena saat tiba di lantai semua energi
potensial telah menjadi energi kinetik (dalam wujud kecepatan) yang sejumlah
dengan energi potensial ketika masih di ketinggian 10 meter, maka setelah
membentur, energi kinetik tersebut akan dirubah kembali menjadi energi potensial
yang besarnya sebesar energi kinetik sebelumnya, yang mana sebesar energi
potensial ketika bola tersebut sebelum di lepaskan. Karena energi potensial
setelah memantul = energi potensial sebelum dijatuhkan, maka dapat kita katakan
tidak ada energi yang hilang dari proses tersebut, atau reversible.
1. sebelum jatuh, 2. sampai di lantai, 3. ketinggian puncak
Namun, pada kenyataanya, tidak ada proses yang benar-benar reversible,
energi tersebut pasti akan hilang karena adanya gesekan, perpindahan panas,
ekspansi mendadak ataupun hal lainya, maka bola yang kita jatuhkan dari gedung
10 meter tadi tidak mungkin memantul lagi pada ketinggian yang sama persis 10
meter, karena adanya gesekan dari udara ketika jatuh, gesekan dengan lantai
ketika sampai di tanah, terjadinya aliran kalor antara bola dengan udara dan lantai
atau timbulnya suara ketika menabrak lantai yang juga mengakibatkan hilangnya
energi, maka proses ini kita katakan irreversible, karena ada energi terbuang yang
tidak dapat kita manfaatkan lagi. Dalam teori termodinamika, suatu proses
kebanyakan diasumsikan sebagai proses yang reversible, karena akan sangat
mempermudah perhitungan, walaupun tidak sama persis dengan apa yang terjadi
di dunia nyata, namun hasil perhitunganya masih dapat di manfaatkan. Ukuran
ketidak-terbalikkan ini terkenal dengan istilah Entropi.
Proses melingkar adalah suatu proses pada suatu system setelah
mengalami beberapa perubahan keadaan, akhirnya kembali pada keadaan semula.
Gb. 2
Gb. 1
Pada proses melingkar, system berubah kemudian kembali ke keadaan
semula. Energy dalam proses melingkar tidak berubah.
Sebuah proses reversible adalah sebuah proses yang berlangsung
sedemikian
sehingga pada akhir proses, system dan keliling local ( local
surroundings) dapat dikembalikan ke keadaan mula-mula, tanpa meninggalkan
suatu perubahan pada sisa universum (rest of universe). Universum disini
digunakan dalam arti teknis, yaitu sempit sekali tanpa suatu pengertian kosmos.
Universum disini artinya tidak lain adalah bagian yang berhingga dari
dunia yang terdiri dari system dan kelilingnya yang dapat mengadakan interaksi
dengan system itu. Sebuah proses yang tidak memenuhi syarat-syarat diatas
disebut irreversible.
Sebagai konsekuensi hukum kedua Termodinamika yang memperlihatkan
arah perubahan alami distribusi energy dan memperkenalkan prinsip peningkatan
entropi, maka semua proses alam adalah irreversible.
Pengubahan usaha menjadi energy dalam sebuah system kalor berlangsung
dengan disertai gejala-gejala seperti gesekan viskositas, inelastisitas, tahanan
listrikndan listeresisi magnetic. Efek-efek ini disebut efek-efek disipatif dan usaha
itu dikatakan terdissipasi.
Proses-proses yang disertai dissipasi usaha menjadi energy dalam
dikatakan menunjukkan irreversible mekanik luar. Irreversibilitas lainnya ialah
irreversibilitas mekanik dalam, irreversibilitas termik, irreversibilitas kimia.
Kalau berbagai macam proses alam diselidiki dengan teliti maka ternyata
bahwa semuanya disertai salah satu dari dua sifat berikut.
1. Tidak dipenuhinya syarat-syarat untuk kesetimbangan termodinamika, yaitu
tidak adanya kesetimbangan mekanik, termik dan kimia
2. Adanya efek disipatif, seperti geseran, viskositas, anelastisitas, tahanan listrik
dan listeresis magnetic.
Maka dapat ditarik kesimpulan, bahwa sebuah proses akan reversible kalau
1. Proses itu berlangsung quasi-statik
2. Proses itu tidak disertai efek-efek desipatif.
Karena tidak mungkin bentuk memenuhi kedua syarat itu dengan
sempurna maka jelaslah bahwa sebuah proses reversible adalah sesuatu yang
hayal atau ideal.
Proses reversible sangat berguna dalam perhitungan teori dalam hal ini,
pengandaian proses reversible dalam termodinamika serupa dengan pengandaian
yang seringkali dijumpai dalam mekanika, misalnya pengandaian kawat yang
tidak bermassa, katrol tanpa geseran dan titik massa.
ADIABATIK, ISOTERMAL, DLL
1.
Isokhorik adalah proses perubahan keadaan yang terjadi pada volume tetap.
Jika gas melakukan proses termodinamika dalam volume yang konstan, gas
dikatakan melakukan proses isokhorik. Karena gas berada dalam volume
konstan (∆V = 0), gas tidak melakukan usaha (W = 0) dan kalor yang
diberikan sama dengan perubahan energi dalamnya. Kalor di sini dapat
dinyatakan sebagai kalor gas pada volume konstan QV.
QV = ∆U
2.
Isobarik adalah proses perubahan keadaan yang terjadi pada volume
konstan.
Jika gas melakukan proses termodinamika dengan menjaga tekanan tetap
konstan, gas dikatakan melakukan proses isobarik. Karena gas berada dalam
tekanan konstan, gas melakukan usaha (W = p∆V). Kalor di sini dapat
dinyatakan sebagai kalor gas pada tekanan konstanQp. Berdasarkan hukum I
termodinamika, pada proses isobarik berlaku
Proses sebelumnya telah dituliskan bahwa perubahan energi dalam sama
dengan kalor yang diserap gas pada volume konstan
QV =∆U
Dari sini usaha gas dapat dinyatakan sebagai
W = Qp − QV
Jadi, usaha yang dilakukan oleh gas (W) dapat dinyatakan sebagai selisih
energi (kalor) yang diserap gas pada tekanan konstan (Qp) dengan energi
(kalor) yang diserap gas pada volume konstan (QV).
3.
Isotermal adalah perubahan sistem, di mana suhu tetap konstan: ΔT = 0.
Ini biasanya terjadi ketika suatu sistem berada dalam kontak dengan
reservior panas luar (mandi panas), dan perubahan terjadi perlahan cukup
untuk memungkinkan sistem untuk terus-menerus menyesuaikan diri
dengan suhu reservoir melalui pertukaran panas. Dalam proses isotermal,
nilai ΔT0 = tapi Q≠0.
4.
Adiabatik adalah tidak ada kalor yang ditambahkan pada sistem atau
meninggalkan sistem (Q = 0). Proses adiabatik bisa terjadi pada sistem
tertutup yang terisolasi dengan baik. Untuk sistem tertutup yang terisolasi
dengan baik, biasanya tidak ada kalor yang dengan seenaknya mengalir ke
dalam sistem atau meninggalkan sistem. Proses adiabatik juga bisa terjadi
pada sistem tertutup yang tidak terisolasi. Untuk kasus ini, proses harus
dilakukan dengan sangat cepat sehingga kalor tidak sempat mengalir
menuju sistem atau meninggalkan sistem
CARA KERJA SIKLUS CARNOT, DIHUBUNGKAN DENGAN HUKUM I
TERMODINAMIKA DAN HUKUM II TERMODINAMIKA
Hukum I Termodinamika mengungkapkan bahwa energi dapat diubah dari
satu bentuk energi ke bentuk energi yang lain. Hukum ini tidak membatasi tentang
arah aliran energi. Dalam kehidupan sehari-hari kita hanya melihat bahwa kalor
dapat mengalir dengan sendirinya dari suatu benda (atau bagian benda) yang
mempunyai temperatur tinggi ke benda lain (atau bagian lain dari benda yang
sama) yang mempunyai temperatur rendah, dan kita tidak melihat proses
sebaliknya. Kita juga dapat melihat bahwa kerja dapat diubah secara keseluruhan
menjadi kalor, tetapi kita tidak dapat mengubah kalor secara keseluruhan menjadi
kerja. Oleh karena itu, masih diperlukan hukum yang mengatur arah proses yang
mungkin terjadi. Hukum ini kita kenal sebagai hukum II Termodinamika
(Mundilarto, 1992).
Menurut Disiki Hadi (1993), bila hukum pertama dan kedua digabungkan
atau digunakan bersama, ternyata dapat
diperoleh beberapa hubungan
termodinamik yang penting. Perumusan hukum pertama termodinamika secara
analitik dalam bentuk diferensial untuk sebarang proses adalah:
d’Q = dU + d’W
(1)
Hukum kedua menyatakan bahwa untuk suatu proses reversibel antara dua
keadaan seimbang.
d’Q = T dS
(2)
Usaha dalam proses reversibel untuk sistem pVT adalahh
d’W = p dV
(3)
Oleh karena itu pada proses reversibel untuk sistem pVT
T dS = dU + p dV
(4)
Persamaan (4) adalah satu perumusan dari gabungan hukum pertama dan kedua
untuk sistem pVT. Untuk sistem lain bentuk persamaan ini tetap berlaku, tetapi
tentu saja besaran-besaran tersebut harus diganti dengan besaran-besaran yang
sesuai.
Persamaan (2) dan (3) hanya berlaku untuk proses reversibel, tetapi
persamaan (4) tidak hanya terbatas pada suatu proses, oleh karena persamaan ini
hanya menyatakan suatu hubungan antara sifat-sifat sistem dan perbedaan antara
nilai sifat-sifat ini, dalam dua keadaan seimbang yang berdekatan. Jadi meskipun
telah digunakan proses reversibel untuk menjabarkan hubungan antara dS, dU,
dan dV, maka setelah hubungan itu ditentukan hubungan itu tetap berlaku untuk
sebarang pasangan keadaan seimbang yang berdekatan.
Misalkan suatu sistem mengalami proses ireversibel antara dua keadaan
seimbang, maka baik persamaan (1) maupun (4) keduanya berlaku, karena yang
pertama benar untuk sebarang proses (reversibel ataupun tidak) dan yang kedua
benar untuk sebarang dua keadaan seimbang. Namun T dS ≠ d’Q dan p dV ≠ d’W,
sebagai contoh, misalnya proses ireversibel yang berkaitan dengan usaha d’W
yang dilakukan untuk mengaduk secara adiabatik zat di dalam sistem pada
volume tetap. Entropi sistem akan bertambah, jadi T dS = 0 karena proses itu
adalah adiabatik. Demikian pula p dV = 0 karena volumenya tetap, tetapi d’W ≠
10.
Yang pertama kali berhasil memecahkan persoalan tentang efisiensi mesin
adalah Sadi Carnot seorang insinyur berkebangsaan Prancis. Sebelum Carnot pada
1824, perbaikan-perbaikan pada mesin uap hanya dari segi kontruksi mekaniknya
saja dan tidak berpedoman pengetahuan tentang asas-asas pokoknya. Sumbangan
Carnot ini bersifat teoritik, tetapi pengaruhnya atas perkembangan dunia industri
dalam abad 19 sangat besar.
Secara singkat, Carnot mengesampingkan soal bagaimana bekerjanya
mesin kalor dan memusatkan perhatiannya pada sifat-sifat yang penting. Pertama,
mesin diberi energi kalor pada temperatur yang relatif tinggi. Kedua, mesin
melakukan usaha mekanik. Ketiga, mesin membuang energi kalor pada
temperatur rendah. Carnot membayangkan bahwa aliran kalor lewat mesin dari
temperatur tinggi ke temperatur rendah seperti halnya aliran air lewat kincir atau
turbin dari tempat yang tinggi ke tempat yang rendah dalam selang waktu tertentu
jumlah air yang masuk ke dalam turbin sama dengan jumlah air yang keluar dan
dari proses ini dihasilkan energi mekanik. Carnot berpendapat bahwa dalam mesin
kalor terjadi proses yang sama, yakni energi mekanik dihasilkan dari aliran kalor
dari temperatur tinggi ke temperatur rendah melewati mesin.
Tetapi jumlah kalor yang dilepaskan oleh mesin adalah lebih kecil dari
pada jumlah kalor yang dimasukkan oleh mesin. Selisih antara keduanya sama
dengan jumlah kalor yang telah diubah oleh energi mekanik. Walaupun konsep
tentang kalor ini salah, Carnot sebenarnya telah berhasil memperoleh ungkapan
yang tepat mengenai efisiensi maksimum dari mesin kalor yang bekerja diantara
dua temperatur tertentu.
Harga efisiensi termal maksimum tercapai jika kerja mesin kalor itu
berlangsung secara bolak-balik (reversible). Mesin kalor yang mempunyai
karakteristik semacam itu pertama kali dikemukakan oleh Sadi Carnot pada 1824,
yang kemudian dikenal sebagai mesin Carnot.
Sejumlah gas ideal berada di dalam silinder dengan dasar konduktor
panas, dinding isolator gesekan, seperti yang ditunjukkan dalam gambar 1.1.
Sebagai bagian dari lingkungan, dalam sistem ini terdapat reservoir panas dengan
temperatur TP dan reservoir dingin dengan temperatur TD.
Gambar 1.1. Bagan Mesin Carnot
Dalam mesin Carnot terdapat satu siklus ideal yang disebut siklus Carnot.
Siklus ini terdiri dari dua proses isotermal yang reversibel dan dua proses
adiabatik yang reversibel juga, seperti ditunjukkan oleh gambar 1.2. Menurut
Mundilarto (1992) di dalam siklus Carnot terdapat empat langkah penting sebagai
berikut:
Gambar 1.2. Siklus Carnot
1. Mula-mula gas berada dalam keadaan kesitimbangan awal dengan tekanan P 1
dan volume V1. Bejana silinder ditempatkan pada reservoir panas dengan
temperatur TP. Gas mengembang secara perlahan-lahan, sehingga mencapai
P2, V2 dan TP. Proses tersebut berlangsung secara isotermik pada temperatur
TP. Selama proses ini sistem gas menyerap kalor sebesar QP dan melakukan
kerja dengan mendorong pengisap ke atas.
2. Bejana silinder ditempatkan pada landasan bukan penghantar, yang
memungkinkan gas mengembang lebih lanjut secara perlahan-lahan sehingga
mencapai keadaan P3, V3 dan TD. Proses ini berlangsung secara adiabatik,
karena tidak ada kalor yang masuk maupun keluar sistem gas. Gas melakukan
usaha dengan mendorong pengisap ke atas dan temperaturnya turun menjadi
TD.
3. Bejana silinder diletakkan pada reservoir dingin dengan temperatur TD,
sehingga gas mengalami pemampatan secara perlahan-lahan sampai mencapai
keadaan P4, V4 dan TD. Selama proses ini gas melepasakan kalor sebesar QD
ke reservoir dingin melalui dasar bejana. Proses pemampatan ini berlangsung
secara isotermik pada temperatur TD. Pengisap melakukan usaha terhadap
sistem gas.
Silinder diletakkan pada landasan bukan penghantar dan gas dimampatkan
secara perlahan-lahan sampai mencapai keadaan P1, V1 dan TP. Kompresi ini
berlangsung secara adiabatik karena tidak ada kalor yang masuk maupun keluar
sistem gas. Kerja dilakukan pada sistem gas sehingga temperatur menjadi TP.
Selama proses ini berlangsung, tidak ada kalor yang keluar atau masuk ke
dalam sistem, tekanan sistem meningkat, dan volumenya berkurang. Menurut
kurva hubungan p–V dari siklus Carnot, usaha yang dilakukan oleh gas adalah
luas daerah di dalam kurva p–V siklus tersebut. Oleh karena siklus selalu kembali
ke keadaannya semula, ΔU siklus = 0 sehingga persamaan usaha siklus (Wsiklus)
dapat dituliskan menjadi
Wsiklus = ΔQsiklus = (Q1 – Q2)
dengan:
Q1
=kalor yang diserap sistem, dan
Q2
= kalor yang dilepaskan sistem.
Ketika mesin mengubah energi kalor menjadi energi mekanik (usaha).
Perbandingan antara besar usaha yang dilakukan sistem (W) terhadap energi kalor
yang diserapnya (Q1) disebut sebagai efisiensi mesin. Persamaan matematis
efisiensi mesin ini dituliskan dengan persamaan
dengan η = efisiensi mesin.
Oleh karena usaha dalam suatu siklus termodinamika dinyatakan dengan
W = Q1 – Q2 maka dapat dituliskan menjadi
Pada mesin Carnot, besarnya kalor yang diserap oleh sistem (Q1) sama dengan
temperatur reservoir suhu tingginya (T1). Demikian juga, besarnya kalor yang
dilepaskan sistem (Q2) sama dengan temperatur reservoir suhu rendah mesin
Carnot tersebut. Oleh karena itu, Persamaan dapat dituliskan menjadi
Keterangan:
η
: efisiensi mesin Carnot
T1
: suhu reservoir bersuhu tinggi (K)
T2
: suhu reservoir bersuhu rendah (K)
Dari Persamaan diatas tersebut, dapat disimpulkan bahwa efisiensi mesin Carnot
dapat ditingkatkan dengan cara menaikkan temperatur reservoir suhu tinggi atau
menurunkan temperatur reservoir suhu rendah.
LEMBAR KONTRIBUSI
1. Novita Purnamasari H (1503646), Mumammad Zainul Arifin (1504013), Putri
Audia AK (1504063)
Mengerjakan cara kerja siklus Carnot dihubungkan dengan termodinamika 1
dan 2; adiabatik, isotermal, dll; reversibel, irreversibel, gambar dan grafik (P
vs S); efisiensi siklus carnot.
2. Jagad Tahari (1504108), Saskiya Khairani (1504067), Rini Suprianni
(1501899)
Mengerjakan jawaban soal; membuat cover; mengedit dan menyusun materi;
mengeprint; menjilid.
DAFTAR PUSTAKA
Anomius. 1978. Hand Book Of Comparative Material Standart. Tokyo:
Engineering.
Bett, Rowluism dan Saville. Thermodynamics for Chemical Engineers. London :
The Artlone Press.
Daubert. Chemical Engineering Thermodynamics. Singapore : Mc.Graw Hill.
Hadi, Dimsiki. 1993. Termodinamika. Yogyakarta: Departemen Pendidikan dan
Kebudayaan
Haryadi, Bambang. Fisika SMA XI IPA. Jakarta: BSE 2009
Mundilarto, dkk. 1992. Fisika Dasar II. Jakarta: Universitas Terbuka
Palupi, Satya Palupy dkk. Fisika untuk SMA/MA Kelas XI. Jakarta: BSE 2009
Smith dan Ness, Van. Introduction to Chemical Engineering Thermodynamics.
Singapore : Mc. Graw Hill.