3. Hukum Termodinamika II dan Mesin kalor

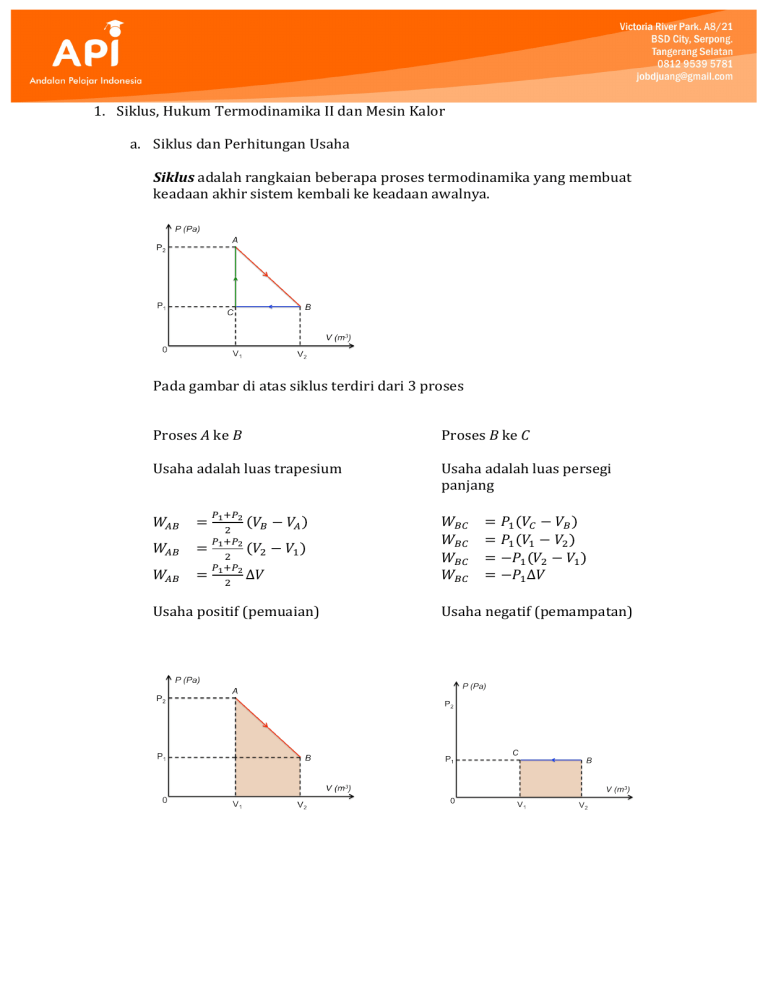
 1. Siklus, Hukum Termodinamika II dan Mesin Kalor a. Siklus dan Perhitungan Usaha Siklus adalah rangkaian beberapa proses termodinamika yang membuat keadaan akhir sistem kembali ke keadaan awalnya. Pada gambar di atas siklus terdiri dari 3 proses Proses A ke B Proses B ke C Usaha adalah luas trapesium Usaha adalah luas persegi panjang ! !!
𝑊!" = 𝑃! 𝑉! − 𝑉!
𝑊!" = ! ! ! 𝑉! − 𝑉!
𝑊!" = 𝑃! 𝑉! − 𝑉!
! !!
𝑊!" = ! ! ! 𝑉! − 𝑉! 𝑊!" = −𝑃! 𝑉! − 𝑉!
!! !!!
𝑊!" = ! ∆𝑉
𝑊!" = −𝑃! ∆𝑉
Usaha positif (pemuaian) Usaha negatif (pemampatan) Proses C ke D 𝑊!" = 𝑃 𝑉! − 𝑉!
𝑊!" = 𝑃 𝑉! − 𝑉!
𝑊!" = 𝑃 0
𝑊!" = 0
Usaha satu siklus 𝐴𝐵𝐶𝐴 𝑊!! = 𝑊!" + 𝑊!" + 𝑊!"
𝑊!!
=
𝑊!!
=
𝑊!!
=
𝑊!!
=
𝑊!!
=
!! !!!
!
!! !!!
!
!
∆𝑉 − 𝑃! ∆𝑉
!
!
!!
∆𝑉 + −𝑃! ∆𝑉 + 0
!
!! !!!
!!
+
−
− 𝑃! ∆𝑉
!!
!
!!
!
−
!!!
∆𝑉
!
∆𝑉
𝑊!! = ! 𝑃! − 𝑃! ∆𝑉
Usaha satu siklus sama dengan luas segitiga atau area yang ada didalam kurva siklus Karena keadaan sistem kembali ke keadaan semula berarti ∆𝑈 = 0 Usaha 𝑊 yang dilakukan oleh sistem dalam satu siklus sama dengan luas area yang ada di dalam kurva siklus dan besarnya sama dengan kalor 𝑄 yang diserap 𝑊 = 𝑄 b. Hukum Termodinamika II dan Mesin Kalor Hukum termodinamika I pada dasarnya adalah hukum kekekalan energi yang mengatakan energi tidak dapat dimusnahkan dan diciptakan namum dapat berpindah atau berubah bentuk. Sesuai hukum kekekalan energi, energi panas es dapat berpindah ke air sehingga es bertambah dingin dan air bertambah panas. Pada kenyataannya hal di atas tidak akan terjadi secara spontan tanpa bantuan suatu alat. Hal sebaliknya akan terjadi secara spontan tanpa bantuan alat yaitu energi panas air akan berpindah atau diserap oleh es sehingga suhu es akan naik dan mencair Hukum termodinamika I tidak menentukan arah perpindahan energi sedang hukum termodinamika II menentukan mana arah perpindahan energi yang mungkin dan yang tidak secara spontan sesuai dengan pengamatan Rudolf Clausius Kalor mengalir secara spontan dari benda bersuhu tinggi ke benda bersuhu rendah dan tidak mengalir secara spontan dalam arah kebalikannya Berdasarkan rumus usaha dalam satu siklus 𝑊 = 𝑄 dan hukum kekekalan energi bahwa kalor yang diserap sistem dapat diubah semuanya menjadi usaha luar. Sesuai dengan pengamatan yang dilakukan oleh Kelvin-­‐Planck Tidak mungkin membuat sebuah mesin kalor yang bekerja dalam suatu siklus yang semata mata menyerap kalor dari sebuah reservoir dan mengubah seluruhnya menjadi usaha luar Mesin Kalor adalah suatu alat yang mengubah energi panas menjadi energi gerak Prinsip kerja mesin kalor (1) Kalor diserap 𝑄! dari sebuah reservoir bersuhu tinggi 𝑇! (2) Mengubah sebagian kalor menjadi usaha luar 𝑊 (3) Melepaskan kalor yang tersisa 𝑄! pada reservoir bersuhu rendah 𝑇! Karena mesin bekerja dalam suatu siklus maka ∆𝑈 = 0 maka 𝑊 = 𝑄! − 𝑄! Efisiensi termal sebuah mesin kalor adalah perbandingan antara usaha yang dilakukan dan kalor yang diserap dari reservoir bersuhu tinggi 𝑊 𝑄! − 𝑄!
𝑄!
𝜂=
=
=1−
𝑄!
𝑄!
𝑄!
c. Siklus Carnot Sardi Carnot mengembangkan metode untuk meningkatkan efisiensi mesin berdasarkan siklus usaha yang disebut siklus Carnot dan mesin Carnot merupakan konsep mesin ideal dengan efisiensi paling tinggi yang tidak pernah ada Siklus Carnot terdiri dari 2 proses isotermis dan 2 proses adiabatis (1) Pada proses isotermal 𝐴𝐵 sistem menyerap kalor 𝑄! dari reservoir bersuhu tinggi 𝑇! dan sistem melakukan usaha 𝑊!" = 𝑄! karena ∆𝑈 = 0 (2) Pada proses adiabatik 𝐵𝐶 sistem mengambil energi dalam dan melakukan usaha 𝑊!" = −∆𝑈 karena 𝑄 = 0 dan suhu turun menjadi 𝑇! (3) Pada proses isotermal 𝐶𝐷 sistem melepaskan kalor 𝑄! ke reservoir bersuhu rendah 𝑇! dan sistem melakukan usaha 𝑊!" = −𝑄! karena ∆𝑈 = 0 (4) Pada proses adiabatik 𝐶𝐴 sistem menambah energi dalam dan melakukan usaha 𝑊!" = ∆𝑈 karena 𝑄 = 0 dan suhu naik kembali ke 𝑇! Usaha total dalam satu siklus adalah 𝑊!! 𝑊!! = 𝑊!" + 𝑊!" + 𝑊!" + 𝑊!"
𝑊!! = 𝑄! − ∆𝑈 − 𝑄! + ∆𝑈
𝑊!! = 𝑄! − 𝑄!
!
!
Khusus untuk mesin ideal atau mesin Carnot berlaku !! = !! sehingga !
Efisiensi termal sebuah mesin kalor ideal adalah 𝑄!
𝑇!
𝜂 =1−
= 1 − 𝑄!
𝑇!
!
d. Mesin Pendingin Prinsip kerja mesin pendingin kebalikan dengan mesin kalor (1) Kalor diserap 𝑄! dari sebuah reservoir bersuhu rendah 𝑇! (2) Lingkungan melakukan usaha terhadap sistem 𝑊 (3) Melepaskan kalor 𝑄! pada reservoir bersuhu tinggi 𝑇! Koefisien performansi mesin pendingin adalah hasil bagi kalor 𝑄! yang diserap dari reservoir suhu rendah dengan usaha 𝑊 yang dibutuhkan dari lingkungan 𝑄!
𝑄!
𝐾! =
=
𝑊 𝑄! − 𝑄!
Koefisien mesin pendingin ideal atau Carnot adalah 𝑇!
𝐾! =
𝑇! − 𝑇!