5.1 PENDAHULUAN Pada chapter 4, kita membicarakan tentang

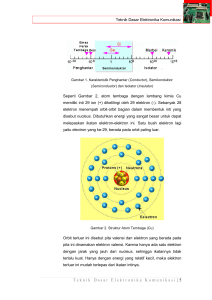
5.1 PENDAHULUAN
Pada chapter 4, kita membicarakan tentang gerak elektron dalam zat padat,
menggunakan model elektron bebas. Model ini disederhanakan, karena potensial
kristal terabaikan. Tapi potensial tersebut tidak dapat sepenuhnya diabaikan jika
kita ingin menjelaskan hasil eksperimen secara kuantitas. Selain itu, beberapa efek
tidak dapat dijelaskan sama sekali tanpa mengambil potensial ini ke dalam
hitungan, seperti yang kita tunjukkan pada akhir bab 4. Karena itu, bab ini
memperlakukan pengaruh potensial kristal pada sifat elektronik zat padat.
Di bagian pertama kita akan mempertimbangkan spektrum energi dari elektron
dalam kristal. Kita akan melihat bahwa spektrumnya berisi pita yang kontinu,
tidak seperti kasus atom, dimana spektrum adalah seperangkat level diskrit. Kita
akan diskusikan sifat dan fungsi gelombang dari pita secara ditail, dan
mengembangkan kriteria yang berguna untuk membedakan logam dari isolator
dalam model pita ini. Lalu kita akan menangani densitas dari bahan dan
permukaan fermi, yang berfungsi sebagai karakteristik yang berguna dari zat
padat.
Elektron pada kristal tetap konstan bergerak. Formula dikembangkan untuk
menghitung kecepatan elektron dan massa efektif. Kita akan belajar efek dari
medan listrik dalam gerakan elektron, lalu menurunkan ekspresi untuk
konduktivitas listrik elektron. Walaupun ekspresi ini mengurangi dengan yang
diturunkan sebelumnya pada chapter 4 di bawah kondisi yang tepat, bentuk yang
kita harus kembangkan di sini adalah lebih umum, dan membawa lebih jelas
faktor konduktivitas yang mempengaruhi fisik.
Resonansi siklotron dan efek hall juga akan di diskusikan lagi dan kita akan
menunjukan bagaimana fenomena ini dapat digunakan untuk memperoleh
informasi dalam zat padat.
Bagian terakhir akan menangani limit dari energi – model pita, dan logam –
insulator transisi.
5.2 Spektra Energi Dalam Atom, Molekul, dan Solid
Pembahasan materi ini dilakukan untuk mendeskripsikan secara kualitatif
spektrum energi dari sebuah elektron yang bergerak dalam kristal solid.
Sebelumnya, pembahasan akan dimulai dengan mempertimbangkan spektrum dari
atom bebas, dengan memperhatikan perubahannya menjadi bentuk solid.
Sebagai contoh konkret, Lithium. Dengan mempertimbangkan atom Lithium
bebas: elektron bergerak dalam sumur potensial, lihar gambar 5.1a. Dengan
penyelesaian persamaan Schrodinger, kita dapatkan deret pemisahan level energi.
Dalam kasus aton hidrogen, level energi ini disimbolkan dengan 1s, 2s, 2p,
danseterusnya. Atom Lithium terdiri dari tiga elektron, dua elektron berada pada
kulit 1s (penuh), elektron ketiga berada pada subkulit 2s.
Dengan pertimbangan situasi dimana dua atom Lithium bergabung untuk
membentuk molekul Lithium, Li2.. Maka potensial pada elektron menjadi dua
kalinya, dilihat pada gambar 5.1b. Energi spektrum di sini terdiri dari satu set
doublet terpisah. Setiam level atomik, yaitu 1s, 2s, 2p, dst, memiliki patahan
dalam dua jarak level terdekat. Karena ada hubungan antara atomik dan level
molekul. Level energi molekular terdiri dari dua sublevel.
Gambar 5.1a
Gambar 5.1b
Gambar 5.1c
Dapat dilihat mengapa level atomik terbagi menjadi hanya dua sublevel, seperti
pada hidrogen molekul. Hal ini dikarenakan: ketika dua atom Li sangat jauh,
pengaruh sebuah atom pada sebuah elektron pada atom lain akan menjadi sangat
kecil, dan kemungkinan akan menjadi masalah. Perkiraan ini, level 1s, 2s, dst
yang tidak bermasalah masing-masing terdegenerasi double. Degenerasi ini valid
hanya jika interaksi antara atom tidak diperhatikan secara menyeluruh. Ketika
interaksi ini diperhatikan, double degenarasi akan meningkat, dan setiap level
terbagi menjadi dua sublevel. Orbit molekular yang berhubungan dengan sublevel
ini biasanya diambil sebagai kombinasi simetris dan asimetris daru hubungan
orbit atomik.
Setiap level molekular dapat mengakomodasi paling banyak dua alektron, dengan
spin berkebalikan, tergantung pada prinsip pencegahan. Molekul Li2 memiliki
enam elektron. Empat elektron dimiliki oleh 1s doblet molekular, yang lain pada
energi terendah dari doublet 2s.
Jumlah pembagian tergantung kekuatan pada jarak memiliki enam elektron.
Empat elektron dimiliki oleh 1s doblet molekular, yang lain pada energi terendah
dari doublet 2s.
Jumlah pembagian tergantung kekuatan pada jarak internulkir dari dua atom pada
molekul. Dua nuklei terdekat, masalah terkuat, dan pembagian terbesar.
Pembagian/ patahan tergantung pada orbital atomik: orbital level 2p lebih besar
daripada level 2s, juga lebih besar dari level 1s. Alasannya adalah jari-jari orbital
1s sangat kecil, orbitnya terikat kuat pada inti. Hal ini tidak dipengaruhi oleh
pertubation. Jadi ledih tinggi energi, patahan akan lebih mudah terjadi.
Pertimbangan di atas dapat digeneralisasikan pada molekul poliatomik Li
berdasarkan nomor atom. Pada molekul 3-atom, setiap level atomik terbagi
menjadi tiga. Pada molekul 4-atom menjadi quadruplet, dst. Padatan Lithium
dilihat sebagai kasus terbatas dengan nomor atomsangat besar, menghasilkan
perbesaran molekul Lithium. Lalu, apa yang terjadi pada bentuk spektrum energi?
Setiap level energi terbagi menjadi N jarak sublevel terdekat, dimana N adalah
nomor atom pada padatan. Tetapi ketika N sangat besar, sekitar 1023 , sublevel
akan mendekat satu sama lain dan membentuk pita energi. Level 1s, 2s, 2p, dst
meningkat pada pita 1s, 2s, 2p lihat gambar 5.1c.
Untuk menggambarkan seberapa dekat tiap-tiap sublevel pada pita, berdasarkan
contoh numerical berikut. Anggap lebar pita 5 eV maka energi intervalnya adalah
5 x 10-23 eV. Dengan nilai yang sagat kecil ini, sublevel masing-masing
dipisahkan, maka diketahui bahwa distribusi pita energi kontinu.
Untuk emnghitung, spektrum energi sebuah padatan terdiri dari satu set pita
energi. Dipisahkan oleh energi gaps- wilayah energi terlarang- yang tidak dapat
diisi elektron. Kondisi sebaliknya pada atom bebas sebuah molekul, dimana
energi yang dibolehkan terbentuk dari level terpisah.
Lebar pita bervariasi, tetapi pada umumnya semakin tinggi pita, akan semakin
lebar, karena energi yang tinggi berhubungan dengan jarak atom yang besar dan
karena perturbation yang kuat, menyebabkan level melewati tempat pertama.
Begitu sebaliknya.
Gambar 5.2
Gambar 5.2 memperlihatkan pita 2s dan 2p untuk logam Lithium, disebut sebagai
fungsi dari kisi konstan a. Dengan catatan, lebar pita meningkat saat a berkurang,
seperti yang dapat diperkirakan, pada jarak interatom yang lebih kecil, pertubation
akan semakin besar. Catatan lain, untuk a < 6a0, pita 2s dan 2p melintasi titik
overlap.
Orbit kristal lebih lama menembus padatan, tidak seperti orbital atomik, dimana
penempatannya mengelilingi atom pada umumnya, dan peluruhan eksponensial
pada atom. Pada kasus ini, kita memilih fungsi gelombang solid sebagai
delocalized orbital. Orbit ini menggambarkan pergerakan gelombang elektron
pada padatan. Prinsip declocalization adalah salah satu dasar untuk semua
fenomena pergerakan elektronik pada padatan, seperti konduksi listrik.
5.3 Pita Energi Pada Solid: Teorema The Bloch
Fungsi The Bloch
ψ(r) =E ψ(r)
(5.1)
Gambar 5.3
Dimana V(r) adalah potensial kristal yang terlihat pada elektron, dan ψ(r) dan E
adalah fungsi kedudukan dan energi dari elektron. Potensial V(r) termasuk
interaksi pada elektron dengan semua atom pada padatan, sama seperti interaksi
dengan elektron lain. Pada poin ini kita membuat pengamatan penting bahwa
potensial V(r) bersifat periodik. Potensial tersebut memiliki simetri seperti kisi,
yaitu
V(r+R) = V(r)
(5.2)
Dimana R adalah vektor kisi. Seperti sebuah potensial yang ditunjukkan gamabr
5.3.
Menurut teorema Bloch, solusi dari 5.1 untuk potensial periodik V(r) adalah
Ψk(r) = eikruk(r)
(5.3)
Dimana fungsi uk(r) memiliki simetri translasi sama dengan kisi, yaitu
uk (r+R) = uk (r)
(5.4)
vektor k adalah kuantitas yang berhubungan dengan momentum partikel.
Pembuktian teorema Bloch,
ψ(r) = f(r) u(r)
dimana u(r) periodik, seperti pada 5.4 dan fungsi f(r) ditentkan. Pada potensial
V(r) perodik, satu syarat semua dapat teramati adalah berhubungan denagn
elektron yang juga periodik. Pada umumnya, kuantitas
dengan
kemungkinan elektron juga periodik. Maka f(r)
Fungsi yang cocok dengan persyaratan untuk semua R adalah suatu bentuk
eksponensial eikr . ini menunjukkan solusi persamaan Schrodinger memiliki
bentuk Bloch (5.3), sebagai buktinya.
Gambar 5.4
Fungsi kedudukan ψ(r)dari bentuk (5.3), diketahui sebagai fungsi Bloch, memiliki
beberapa properti menarik
a) Fungsi ψ(r) memiliki bentuk gelombang pesawat bergerak, digambarkan
sebagai faktor eikr dengan pendapat bahwa elektron meningkat menembus
kristal seperti partikel bebas. Efek dari fungsi uk (r) adalah untuk
memodulasi gelombang ini sehingga amplitudo berosilasi periodik dari
satu sel ke sel selanjutnya, seperti pada gambar 5.4, tetapi hal itu tidak
berpengaruh pada karakter dasar dari fungsi kedudukan gelombang
berjalan.
Jika elektron benar-benar bebas, fungsi kedudukan ψk diberikan oleh
(1/V1/2) eikr. Fungsi uk (r) konstan. Tetapi elektron tidak bebas ketika
elektron berinteraksi dengan kisi, dan interaksi ini menentukan karakter
khusus fungsi periodik uk.
b) Karena elektron sebagai gelombang dari vektor k, elektron memiliki
panjang gelombang DeBroglie λ=2π/k. Dan momentumnya
P=
c) Fungsi The Bloch ψ(r) adalah orbit kristal, yang dilokalisasi menembus
padatan dan tidak dilokalisasi mengelilingi atom umumnya. Elektron
dibagi berdasarkan kristalnya. Hal ini sesuai dengan properti a) di atas,
dimana kita mendeskripsikan elektron sebagai gelombang berjalan.
Dengan catatan bahwa fungsi ψ(r) dipilih bahwa kemungkinan distribusi
elektron
periodik pada kristal.
Pita Energi
Spektrum energi sebagai hasil dari penyelesaian persamaan Schrodinger
(5.1). Persamaan tersebut dalam bentuk lain. Subtitusi untuk ψ(r) dari
bentuk (5.3) The Bloch, dan eliminasi faktor eikr, maka didapatkan
uk(r) =Ek uk(r)
(5.6)
Persamaan gelombang untuk fungsi periodik uk(r). Ini adalah persamaan
nilai eigen, seperti persamaan Schrodinger, dapat juga diselesaikan dengan
cara yang sama. Sebagai catatan, operator dalam tanda kurung adalah
fungsi eksplisit dari k, dan kedua fungsi eigen dan nilai eigen tergantung
pada k. Sebuah persamaan nilai eigen memimpin munculnya beberapa
solusi. Untuk setiap nilai k, kita dapat menemukan banyak solusi,
diberikan satu set enerdi terpisah Ei,k, E2,k, ..., seperti pada gambar 5.5.
energi tergantung pada k, energi menyebabkan kotinuitas seperti k yang
berbeda pada jangkauan nilai. Setiap level dicontohkan sebagai sebuah
pita energi, yang diperlihatkan gambar. Nilei eigen energi ditulis sebagai
En(k), dan n sebagai indeks pita.
Gambar 5.5
Nomor pita adalah besar, biasanya tak terbatas, tetapi hanya yang paling
rendah yang ditempati oleh elektron. Setiap pita ditutupi oleh jangkauan
energi tertentu, sepanjang nilai terendah dan tertinggi yng diambil pada
jarak-k. Interval energi antara pita menentukan gap energi, dimana energi
terlarang tidak dapat ditempati elektron.
k adalah vektor kuantitas, diagram seperti gambar 5.5 adalah plot dari pita
energi pada hanya satu tujuan umum pada ruang k. Jika pita ini
ditempatkan pada tujuan k berbeda, penampakannya akan berubah, secara
umum. Penggambaran lengkap dari pita mensyaratkan satu spesifikasi
nilai energi pada ruang-k. Seringkali hal ini ditunjukkan dengan gambar
kontur energi dalam ruang-k untuk beberapa pita.
Potensial Kristal
Pembahasan kali ini tentang potensial kristal V(r) yang bekerja pada
elekton. Potensial ini terdiri dari dua bagian: interaksi elektron dengan
pusat ion yang membentuk kisi, dan interaksi dengan elektron Bloch lain
yang bergerak melintasi kisi. Pada Sodium padat, sebagai contoh, sebuah
elektron pada pita 3s berinteraksi dengan ion Na+ membentuk struktur bbc,
sama baiknya dengan elektron lain pada pita ini. Kita dapat menulis V(r)
sebagi hasil
V(r)=Vi(r) + Ve(r)
(5.7)
Dimana bagian pertama sebelah kanan menunjukkan interaksi dengan ion
pusat dan yang kedua interaksi dengan elektron. Bagian ionik dapat
dituliskan, sebagai berikut:
(5.8)
Dimana
adalah potensial dari ion yang terdapat pada vektor
kisi Rj, seperti pada gambar 5.5a, dan penjumlahan semua ion. Potensial
Vi(r) memiliki sifat periodik yang sama dengan kisi.
Gambar 5.6
Potensial elektronik Ve(r), disebut juga interaksi elektron-lektron,
menunjukkan beberapa lompatan yang membuat penjagaan menjadi sangat
sulit. Pertama, kita dapat mengevaluasi bagian ini hanya jika kita tahu
kedudukan untuk semua elektron-elektron lain, tetapi kedudukan ini tidak
diberikan dalam lanjutan. Kedua, potensial V(r) buaknlah periodik ketat,
dimana elektron dalam gerak konstan melintasi kisi. Ketiga, penjagaan
yang baik harus benar-benar mempertimbangkan pergerakan elektron
secara simultan, bukan satu elektron dalam satu waktu, seperti yang telah
kita lakukan. Ini adalah beberapa masalah yang sering dihadapi dalam
fisika zat padat.
Melihat kesulitan ini, akan baik jika interaksi elektron-elektron berubah
menjadi cukup lemah, untuk alasan yang diberikan pada bagian 4.3,
karena fakta ini membuat kesulitan di atas lebih tidak serius daripada
sebaliknya. Dampak utama dari interaksi ini adalah distribusi elektron
mereka sendiri secara umum mengelilingi ion, karena itu interaksi
elektron-ion lemah, bahkan dalam jangka lama.
Jadi, kita dapat menulis perkiraan untuk potensial sebagai
Dimana
adalah potensial ion yang terletak pada titik kisi
Rj. Dan dipastikan karena potensial ini peruiodik, ini memenuhi
persyaratan teorema Bloch. Gambar 5.6b menunjukkan potensial kristal
untuk Na.
5.4 Pita Enrgi di ruang-k : Zona Brillouin
Energi eigenvalue En(k) untuk pita energi memiliki banyak sifar simetri
yang berguna ketika pita energi ini diletakkan di ruang-k
Zona Brillouin
Zona Brilloin ditemui ketika terjadi difraksi Bragg dari sinar-x. Ketika
bidang normal yang membagi dua vektor kisi balik, daerah itu ditutup
antara antara bidang tersebut dari variasi Brillouin Zone.
Seperti yang telah kita pelajari sebelumnya, syarat terjadinya difraksi
2
(k+G)
= k2 :
Bragg
adalah
k2 + 2k .G + G2 = k2
Untuk kristal satu dimensi, k berhimpit dengan G sehingga 2k.G = 2k.G
cos 0 = 2k.G, Dengan demikian nilai k = + ½ G, dimana G = n(2п/a)
adalah vektor kisi respirok, dan n adalah bilangan bulat. Sehingga
k= + ½ G = + n(п/a)
Difraksi pertama terjadi dan celah energi pertama terjadi untuk nilai k = +
(п/a). Cdaerah antara - п/a dengan п/a disebut Daerah Brilloiun zona
pertama
Ksi persegi yang resiprokal , dan kisi persegi di tepi sama dengan 2п/a
(liat gambar 5.7). daerah tengah tertutup yang terdekat di sekeliling daerah
asal adalah zona pertama. Daerah gelap membentuk zona kedua.
Semua zona memiliki area yang sama, tanpa memperhatikan kompleksitas
dari zonanya. Ini bisa dilihat dari gambar zona kedua yang memiliki area
sama dengan zona pertama yaitu (2п/a)2 . kesaman ini berlaku untuk
semua zona. Persamaan area dari zone Brillouin ini benar untuk semua kisi
bidang tidak hanya pada kisi persegi.
Bahan simetri
Setiap pita energi mengikuti simetri bahan
i) En(k+G) = En(k)
ii)
En(-k) = En(k)
iii)
En(k) memiliki simetri rotasi yang sama seperti kisi sebenarnya.
Bahan (i) mengindikasikan En(k) periodik, dengan periode sama dengan
vektor kisi resiprokal. Dengan kata lain, dua titik di ruang-k yang
berhubungan dengan lainnya dngan perpindahan sama seperti vektor kisi
resiprokal memiliki energi sama.
sebagai
contoh, pada gambar 5.9 pada point P1, P2, P3 energinya sama,
karena P2 berhubungan dengan P1 dengan translasi G2. P3 berhubungan
dengan P1 dengan transasi G1. G1 dan G2 adalah vektor kisi resiprokal.
Gambar 5.9 b menggambarkan bagaimana dengan menggunakan simetri
tranlasi ini,berbagai bagian zone kedua ditranslasikan dengan vektor kisi
resiprokal akan pas seperti zone pertama. Setiap dua area yang
dihubungkan dengan sebuah panah adalah sama. Demikian juga, zona
yang lebih tinggi bisa ditranslasikan pas dengan zona pertama. Itu
sebabnya, kita hanya membatasi perhatian kita ke zona pertama saja,
selama bagian ini memuat semua informasi yang dibutuhkan.
Pembalikan bahan (ii) menunjukkan bahwa simetri pita energi dengan
pembalikan sekitar k=0. karena itu, di gambar 5.9(a), energi di titik P1
sama denan P1
Bahan (iii) menegaskan bahwa pita energi memiliki simetri rotasi yang
sama seperti kisi sebenarnya. Misalnya di kisi persegi, energi seharusnya
menunjukkan simetri rotasi dari persegi. Sejak simetri ini mematuhi rotasi
п/2 (dan perkaliannya), ini mengikuti seperti gambar 5.9 (c) bahwa energi
di titki Q1,Q2,Q3 sama dengan titik P1, karena titik-titik ini diperoleh dari
P1 dengan rotasi simetri.
Pada gambar 5.9(d) kontor energi disketsa untuk sebuah pita di zone
pertama dari kisi persegi. Gambar ini memenuhi berbagai bahan simetri
yang digambarkan sebelumnya.
Simetri bahan sangat dibutuhkan karena kita bisa menggunakannya untuk
mengurangi keterlibatan kerja untuk menentukan pita energi.
Penyimpanan kerja bahkan lebih bsar di kasus tiga dimensi. Mislanya di
kasus kisi kubik, pita butuh dirinci secara bebas dengan hanya 1/48 tingkat
dari zona pertama.
Dinyatakan bahwa simetri bahan mengacu kepada pita yang sama. Mereka
memegang setiap pita secara terpisah, tetapi jangan hubungkan satu pita ke
pita lain.
5.5 Nomer di tiap keadaan
Kita menyatakan fungsi Bloch dengan Ψn,k yang terindikasi bahwa nilai
index pita n dan vektor k menetukan keadaan elektron atau orbital. Kita
menunjukkan bahwa nomor robit di sebuah pita dalam zona pertama sama
dengan nomer dari sel unit di kristal.
Pertimbangkan dalam kasus satu dimensi, dimana fungsi Bloch memiliki
bentuk
Ψk(x) = eikxUk(x), nilai k hanya diberikan oleh
k = n2п
L
Dimana n= 0, +1, +2,etc
nomer keadaan di zona pertama dengan panjang 2п/a sama dengan :
(2п/a)/ 2п/L = L/a = N
5.6 Model Elektron Hampir Bebas
Diasumsikan bahwa potensial kristal sangat lemah. Sehingga elektron pada
dasarnya berperilaku seperti sebuah partikel bebas. Pengaruh dari potensial ini
akan diperlakukan dengan metode perturbasi(gangguan), yang hasilnya
diharapkan sevalid potensialnya lemah.
Pada model elektron bebas nilai energi didistribusikan secara esensialdari nol
sampai tak hingga. Kita lihat dalam Bab sebelumnya bahwa
dimana, untuk kondisi batas periodik pada kubus sisi L,
dan fungsi gelombang elektron bebas yakni:
ini mewakili gelombang berjalan dan membawa momentum p = hk.
5.7 Celah Energi dan Refleksi Bragg
Kita tahu bahwa refleksi Bragg adalah fitur karakteristik perambatan gelombang
dalam kristal. refleksi Bragg pada gelombang elektron dalam kristal merupakan
penyebab
celahenergi(energy gaps). (Pada refleksi gelombang Bragg, solusi seperti
persamaan Schrodinger tidak ada, seperti pada Gambar. 2.) celahenergi ini sangat
penting dalam menentukan sebuah solid merupakan insulator atau konduktor.
Kami menjelaskan secara fisika asal celah energi dalam masalah sederhana dari
sebuah solid linier pada kisi a. Bagian energi yang rendah pada struktur band
ditampilkan secara kualitatif seperti ditunjukkan pada Gambar. 2, dalam (a) untuk
seluruh elektron bebas dan (b) untuk elektron hampir bebas, tetapi dengan celah
energi pada
. Kondisi Bragg
untuk difraksi gelombang
vektor k dalam satu dimensi
dimana
adalah vektor kisi resiprokal dan n adalah bilangan bulat.
Refleksi pertama dan celah energi pertama terjadi pada
Daerah dalam
ruang к antara
dan
adalah zona Brillouin pertama kisi ini. celah
energi lain terjadi karena nilai-nilai lain dari integer n.
Kita dapat membentuk dua standing wave berbeda dari dua gelombang berjalan
yakni:
Gelombang berdiri diberi label (+) atau (-) berdasarkan apakah terjadi perubahan
ketika tanda –x disubstitusikan untuk nilai x.
5.14 Dinamika Elektron dalam Medan Listrik
Ketika sebuah medan listrik digunakan dalam sebuah benda padat, elektron yang
ada di dalam benda padat akan mengalami percepatan. Kita bisa mempelajari
gerakkannya paling mudah pada ruang k. Misalkan medan listrik ε diaplikasikan
pada kristal. Sebagai hasilnya, sebuah elektron di dalam kristal menghasilkan
gaya F = -eε, dan oleh karena itu membuat perubahan pada energinya. Rata-rata
penyerapan energi oleh elektron adalah
(5.77)
dimana persamaan di sebelah kanan mengekspresikan kekuatam menyerap oleh
objek yang bergerak. Jika kita menulis
dan menggunakan persamaan (5.70) untuk v, lalu subtitusikan ke (5.77), kita
menemukan hubungan sederhana
(5.78)
Ini menunjukkan bahwa rata-rata dari perubahan k adalah proporsional untuk –
dan terletak pada arah yang sama- gaya listrik F (contoh : berlawanan dengan
medan ε, dengan mengutamakan muatan negatif elektron). Hubungan ini sangat
penting dalam dinamika dari elektron Bloch, dan ini dikenal sebagai teorema
percepatan.
Persamaan (5.78) belum terduga. Kita telah menandai fakta bahwa vektor hk
berkelakuan seperti momentum dari elektron Bloch (seksi 5.3). Pada konteks
tersebut, persamaan (5.78) secara sederhana menyatakan bahwa rata-rata waktu
dari perubahan momentum adalah sebanding dengan gaya, dimana sesuai dengan
hukum Newton kedua.
Sekarang kita mempertimbangkan akibat dari teorema percepatan, dimulai dengan
kasus 1 dimensi. Persamaan (5.78) bisa ditulis dalam persamaan
(5.79)
Menunjukkan bahwa vektor gelombang k naik seragam dengan waktu. Jadi,
sebagai kenaikan t, elektron melintasi ruang k pada rata-rata, sebagaimana
ditunjukkan pada gambar 5.34. Jika kita menggunakan skema zona berulang,
elektron, dimulai dari k=0, sebagai contoh, bergerak naik sampai meraih puncak
(titik A) dan kemudian mulai untuk turun sepanjang BC. Jika kita menggunakan
skema zona redusi, kemudian elektron melewati pinggiran zona A, segera terlihat
kembali pada titik ekuivalen A’, kemudian dilanjutkan untuk turun sepanjang
garis A’B’C’. Ingat kembali, menurut ciri simentri translasi dari seksi 5.4, titik B’,
C’ masing-masing equivalen dengan titik B, C jadi kita bisa menggunakan kedua
skema tersebut.
Ingat bahwa kehadiran dari medan listrik, elektron bergerak konstan pada ruang k,
ini tidak pernah beristirahat. Juga ingat bahwa pergerakan di ruang k adalah
periodik pada skema zona redusi, setelah melewati zona sekali, elektron
mengulang pergerakan. Periode dari pergerakan sudah ditemukan, pada basis dari
persamaan (5.79) menjadi
(5.80)
Gambar 5.34(b) menunjukkan kecepatan dari elektron sebagai perlintasan garis k.
Dimulai dari k=0 sebagai waktu yang berlalu, kecepatan meningkat, mencapai
maksimum, berkurang, dan kemudian lenyap pada zona pinggir. Elektron berputar
dan mendapatkan kecepatan negatif dan seterusnya. Kecepatan yang kita
diskusikan adalah kecepatan sebenarnya seperti contoh kecepatan fisika biasanya.
Ini mengikuti bahwa elektron Blonch, di hadapan medan listrik statis, membuat
gerakan periode osilasi pada ruang sebenarnya, sama sekali tidak sama dengan
elektron bebas. Ini merupakan salah satu konklusi yang mengejutkan pada
dinamika elektron pada kristal.
Pergerakan osilasi belum disebutkan diatas belum bisa diobservasi dan alasannya
tidak sulit didapat. Periode T dari persamaan (5.80) sekitar 10-5 s untuk nilai
parameter yang biasa digunakan, dibandingkan dengan waktu tumbukkan elektron
pada temperatur ruangan. Jadi elektron mengalami banyak tumbukkan, sekitar
109, pada sebuah siklus. Akibatnya pergerakan osilasi dibersihkan keluar.
Sekarang bedasarkan situasi dari dua dimensi (gambar 5.35). Ketika sebuah gaya
listrik F diaplikasikan, dimulai dari beberapa titik P yang berubah-ubah, bergerak
pada titik P1, ini terlihat kembali pada P1’, dilanjutkan pada P2, dan muncul
kembali pada titik P2’. Ini mengikuti gari sselang seling seperti yang terlihat pada
gambar 5.35 (a). Jika kita masih menggunakan skema zona berulang (gambar
5.35b), kemudian garis dari elektron di ruang k akan menjadi garis lurus
sederhana P P1 P’P2’ P’P3’ (ingat bahwa P’2’ adalah setara dengan P2, P’3’
pada P3, dll). Ini menjadi salah satu situasi dimana skema zona berulang
membuktikan lebih mudah dari pada skema zona perpanjangan.
5.15 Dinamika Massa Efektif
Ketika medan listrik diaplikasikan pada sebuah kristal, elektron Bloch mengalami
percepatan. Ini bisa dihitung dengan menggunakan berikut : ketika percepatan
adalah turunan dari kecepatan, kita mempunyai
(5.81)
Dimana kita telah memilih untuk memperlakukan kasus 1 dimensi terlebih
dahulu. Tetapi kecepatan adalah fungsi dari vektor gelombang k, dan akibatnya
adalah persamaan di atas ditulis menjadi
dimana, ketika kita mensubtitusikan untuk kecepatan dari persamaan (5.72), dan
untuk dk/dt dari persamaan (5.78), menghasilkan persamaan
(5.82)
Bentuk persamaan ini sama dengan bentuk hukum Newton kedua, sehingga bisa
didefinisikan dinamika massa efektif m* dengan hubungan
(5.83)
Jadi, sepanjang pergerakan di dalam sebuah medan listrik diperhatikan, elektron
Bloch berkelakuan seperti elektron bebas yang memiliki massa dalam persamaan
(5.83).
Massa m* terbalik sebanding dengan kelengkungan; dimana kelengkungannya
besar – karenad2E/dk2 juga besar – massanya kecil; kelengkungan kecil
mengakibatkan massanya besar (gambar 5.36).
Sebelumnya kita telah menggunakan konsep dari massa efektif (bagian 5.6 dan
5.8). Situasi tersebut sekarang diganti dengan – kasus kenyataan spesial –
hubungan biasa (5.38). Jadi, jika energinya adalah pangkat dua dari k
(5.84)
dimana α konstan. Sehingga menghasilkan persamaan (5.38)
(5.85)
Dimana sebanding dengan persamaan (5.84) menjadi E = h2k2/2m*, bentuk
sederhana.
Gambar 5.37 (a) dan (b) menunjukkan, secara berurutan, stuktur dan massa efektif
m*, yang terakhir dihitung bedasarkan persamaan (5.83). Dekat dengan bagian
bawah gambar, massa efektif m* memiliki nilai positif, karena hubungan kuadrat
sesuai dekat dengan bagian bawah. Tetapi sebagai penambahan k, m* tidak lagi
konstan, sekarang menjadi fungsi k, karena hubungan kuadrat tidak valid.
Ingat juga bahwa di luar titik perubahan kc massa m* menjadi negatif, sejak
daerahnya dekat dengan puncak, dan massa diharapkan menjadi negatif (bagian
5.6 dan 5.8).
Massa negatif dapat dilihat dinamis dengan meniadakannya, sesuai dengan
gambar 5.34, pengurangan kecepatan untuk k>kc. Jadi percepatannya negatif
contoh lawanlah gaya yang diberikan, gunakan massa negatif. Ini berarti bahwa
pada daerah ruang-k kisi eksert seperti perlambatan (atau pengereman) gaya pada
elektron bahwa ia mengatasi penggunaan gaya dan menghasilkan percepatan
negatif.
Hasil di atas dapat diperpanjang untuk tiga diemnsi. Percepatannya adalah
Jika kita menulis pada bidang kartesius, dan menggunakan persamaan (5.70) dan
(5.78), kita dapat menemukan bahwa
, i, j = x, y, z
Dimana digunakan untuk mendefinisikan massa efektif menjadi
i,j = x, y, z
(5.86)
Massa efektif sekarang menjadi urutan kedua tensor dimana ada sembilan
komponen.
Ketika hubungan dispersi dapat ditulis sebagai berikut
(5.87)
Kemudian gunakan persamaan (5.86) untuk mencari massa efektif dengan tiga
komponen m*xx = h2/2α1, m*yy = h2/2α2, dan m*zz = h2/2α3. Pada kasus ini
massa dari elektron adalah anisotropik, dan bergantung pada arah dari gaya luar.
Ketika gaya sepanjang sumbu-k, elektron merespon dengan massa m*xx, ketika
gaya berkorespondensi di arah ky memunculkan massa efektif m*yy. Sebuah
hubungan tipe (5.87), berkorespondensi dengan kontor elipsoid, ini biasa terjadi
pada bahan semikonduktor, contoh Si dan Ge. Ingat bahwa pada kasus ini, tidak
seperti kasus elektron bebas, percepatan tidak seperti itu, pada umumnya, sama
arah dengan gaya yang digunakan.
Ini juga mungkin terjadi pada α (5.87) negatif. Ini menunjukkan bahwa hubungan
massa adalah negatif, ketika arah lainnya menunjukkan massa positif. Hal ini
sangat berbeda dengan kebiasaan dari elektron bebas.
Konsep massa efektif sangat berguna, ini sering digunakan untuk menyelesaikan
masalah dari elektron Blonch dengan cara menganalogikannya dengan elektron
bebas. Meskipun demikian, elektron Blonch menunjukkan banyak sifat biasa
dimana asing untuk elektron bebas.
5.16 Momentun, momentum kristal, dan physical origin of the effective
mass
Dinyatakan pada beberapa kejadian pada elektron Bloch dalam keadaan k
menunjukkan memiliki momentum sebesar ħk. Pada dasarnya ada tiga alasan
berbeda yang mendukung pernyataan ini.
a) Fungsi Bloch memiliki persamaan
b) Ketika medan listrik diterapkan, vektor gelombang terhadap waktu
berdasarkan
Menyatakan bahwa ħk sebagai momentum.
c) Pada proses tumbukan yang menyertakan elektron Bloch, elektron
menambahkan/ memperbesar elektron sebanding dengan ħk.
Alasan-alasan ini cukup penting untuk menjamin bahwa ħk adalah
momentum.untuk membuat menjadi lebih jelas, tunjukkan vektor ħk dengan
,
yaitu
Ini dinyatakan sebagai momentum kristal.
5.17 The hole
Lubang yang terjadi di pita adalah diisi penuh kecuali untuk satu tempat kosong.
E
hole
0
k
Konsep lubang merupakan satu teori penting, terutama dalam semikunduktor
sebagai sifat dasar dalam mengoperasikan beberapa barang, seperti transistor.
Bila lubang ditempatkan pada vektor
seperti pada gambar, densitas arus pada
sistem adalah
Bila jumlah pengisian pita adalah nol, densitas arunya juga sebanding dengan
5.18 Konduktivitas listrik
Kami membahas konduktivitas listrik sebelumnya sehubungan dengan model
elektron bebas, di mana kita diperoleh hasil
N kuantitas adalah konsentrasi elektron konduksi atau valensi dan τ_F adalah
waktu tabrakan untuk sebuah elektron pada permukaan Fermi. Sekarang mari kita
berasal ungkapan yang sesuai untuk konduktivitas listrik dalam kerangka teori
band.
Ketika sistem berada pada kesetimbangan, ketika tidak ada medan listrik FS ini
berpusat tepat di asal. Akibatnya arus bersih adalah nol, karena kecepatan elektron
membatalkan berpasangan. Itu adalah untuk setiap elektron dalam K negara yang
kecepatan adalah v (k) elektron lain ada di K negara yang kecepatan v (-K) =-v
(k) hanya kebalikan dari yang pertama. Hasil ini ditemukan dalam model bebaselektron, juga terus baik dalam teori band, dan rekening untuk hilang dari arus
pada kesetimbangan.
Ketika medan listrik diterapkan, setiap elektron perjalanan melalui k-ruang pada
tingkat yang seragam, seperti yang dibahas.
Dimana
adalah perpindahan dalam waktu δt interval. Karena elektron
biasanya hidup untuk yang setara dengan interval waktu τ tabrakan, perpindahan
rata-rata
(5.103)
Akibatnya FS dipindahkan secara kaku dengan jumlah ini, seperti yang
ditunjukkan pada gambar 5.40 (b). sekarang ada beberapa elektron yang tidak
dikompensasi, dibatalkan oleh elektron lain dan yang ditunjukkan oleh wilayah
menetas salib berbentuk bulan sabit. Mereka memberikan kontribusi yang bersih
saat ini
Kepadatan arus ini dapat dihitung sebagai berikut: ia telah diberikan
(5.104)
Dimana
adalah komponen kecepatan Fermi dalam arah x dan bar
menunjukkan nilai rata-rata.
Perhatikan
bahwa
terkompensasi,
memberikan
konsentrasi
tidak
yang kepadatan negara di FS dan δE energi menyerap
energi yang diserap oleh elektron dari lapangan. Tidak ada yang
menggantikan
elektron
dari satu (5.103) memperoleh
dan
Dimana waktu tabrakan telah ditunjuk sebagai
dalam sebanyak Jelas kita
berhadapan dengan elektron berbaring di FS. Perhatikan bahwa saat ini dalam
arah yang sama sebagai bidang.
Untuk FS bola ada simetri bola dan maka salah satu dapat menulis
yang ketika disubstitusikan ke (5,105) akhirnya mengarah ke
ekspresi berikut untuk listrik daya konduksi
(5.106)
Perhatikan bahwa σ tergantung pada kecepatan Fermi dan waktu tabrakan namun
juga mencatat ketergantungan pada kerapatan s negara di FS,
. Seringkali
ini merupakan faktor dominan dalam menentukan konduktivitas sebagaimana
yang akan kita lihat segera
Ekspresi (5.106) lebih umum dari rumus elektron bebas (5,102) dan jauh lebih
bermakna. Persamaan (5,102) menunjukkan konduktivitas yang dikendalikan
terutama oleh n, konsentrasi elektron. Namun, konduktivitas sebenarnya
dikendalikan terutama oleh kepadatan g negara
sebagai gantinya. Dalam
batas yang sesuai, ekspresi (5.106) mengurangi untuk (5,102) sebagai kasus
khusus seperti itu harus. Untuk membangun ini kita menggunakan hubungan
.
and
yang kita
temukan mengurangi (5.106) untuk (5.102)
Gambar 5.41 menunjukkan kepadatan negara untuk khas yang solid,
menunjukkan posisi tingkat Fermi untuk logam monovalen dan juga untuk
isolator. Dalam logam tingkat
terletak dekat bagian tengah dari band mana
adalah besar, mengarah ke konduktivitas besar menurut (5.106). dalam
isolator tingkat E_F yang benar di bagian atas band, di mana
.
sehingga konduktivitas adalah nol, meskipun fakta bahwa kecepatan Fermi, yang
juga muncul dalam (5.106) adalah sangat besar.
Ekspresi (5.106) meskipun terbatas pada kasus di mana FS bola, ini berguna
dalam mengungkap peran penting yang dimainkan oleh kepadatan negara.
Hasilnya mungkin umum untuk memasukkan pengaruh bentuk FS lebih
kompleks, yang sering menyebabkan ekspresi berat.
Aspek lain yang penting dari proses konduksi listrik dan fenomena transportasi
pada umumnya adalah bahwa mereka memungkinkan kita untuk menghitung
waktu tabrakan
5.19 Dinamika elektron dalam medan magnet: resonansi siklotron dan efek
hall
Persamaan dasar gerak menggambarkan dinamika dalam medan magnetic
(5.107)
dimana sisi kiri adalah waktu turunan dari momentum kristal dan sisi kanan gaya
Lorentz dikenal karena medan magnet. Persamaan ini adalah satu masuk akal
dalam terang diskusi dalam bagian 5.14 dan 5.16 di mana kita menyimpulkan
bahwa momentum kristal biasanya bertindak sebagai akrab juga mungkin cerived
dari perhitungan kuantum rinci. Menurut (5,107) perubahan k dalam interval
waktu δt diberikan oleh
(5.108)
yang menunjukkan bahwa elektron bergerak dalam ruang k sedemikian rupa yang
perpindahan δk tegak lurus terhadap bidang yang didefinisikan oleh v dan B. sejak
δk tegak lurus terhadap B ini berarti bahwa lintasan elektron terletak pada bidang
normal terhadap medan magnet. Selain itu δk tegak lurus ke v yang sebanyak v
adalah normal untuk kontur energi di ruang k berarti bahwa δk terletak di
sepanjang seperti kontur. Puting dua bit informasi bersama-sama kita
menyimpulkan bahwa elektron berputar sepanjang kontur energi normal medan
magnet ara 5,42 dan dalam mode berlawanan.
Perlu dicatat juga bahwa, karena elektron bergerak sepanjang kontur energi tidak
ada energi diserap dari atau dikirim ke medan magnet dalam perjanjian dengan
fakta-fakta terkenal tentang interaksi muatan listrik dengan medan magnet.
gambar 5.42 menunjukkan gerakan elektron dalam ruang k adalah siklik sejak
setelah waktu tertentu elektron kembali ke titik dari mana itu dimulai. Periode T
untuk gerak adalah menurut (5,108) yang diberikan oleh
(5.109)
Dimana lingkaran pada tanda integrasi menunjukkan bahwa integrasi ini harus
dilakukan selama siklus lengkap dalam ruang k orbit tertutup. Dalam (5,109)
diferensial δk diambil sepanjang perimeter orbit, sementara v (k) adalah besar dari
kecepatan elektron orbit normal. Juga mencatat bahwa untuk menurunkan (5,109)
dari (5,108) kita telah menggunakan fakta bahwa v adalah normal untuk B sejak
lintasan elektron terletak pada bidang normal B.
Para
frekuensi sudut yang terkait dengan gerakan tersebut
yang
terang (5,109) diberikan oleh
(5.110)
Ini adalah frekuensi siklotron untuk elektron Bloch. Ini adalah generalisasi dari
frekuensi siklotron (4.38) diturunkan untuk model elektron bebas
Kami menyimpulkan bahwa gerakan dari elektron Bloch Dalam medan magnet
adalah generalisasi alami dari gerak elektron e bebas di bidang yang sama. Sebuah
elektron bebas menjalankan gerak melingkar dalam ruang kecepatan sepanjang
kontur energi dengan frekuensi
. Sebuah elektron Bloch
mengeksekusi sebuah gerak siklotron sepanjang kontur energi dengan frekuensi
yang diberikan oleh (5.110). kontur energi dalam kasus yang terakhir ini mungkin
tentu saja sangat rumit.
Ketika standar dari
berlaku frekuensi
dalam (5.110) dapat dengan
mudah dihitung. Siklotron orbit adalah lingkaran dalam kasus ini dan dalam
mengevaluasi integral kami mencatat bahwa
sepanjang lintasan ini kontur. Demikian
Yang apabila disubstitusikan ke (5.110) menghasilkan
yang konstan di
Hal ini seperti yang diharapkan setuju dengan hasil untuk model elektron bebas.
Tapi tentu saja Persamaan. (5.110) lebih umum dari hasil elektron bebas dan
berlaku untuk satu kontur bentuk sewenang-wenang meskipun mengevaluasi
integral mungkin menjadi sangat membosankan. Pada bagian masalah pada akhir
bab ini, Anda akan diminta untuk mengevaluasi ω_c untuk kontur yang walaupun
lebih rumit daripada dalam model elektron bebas masih cukup sederhana untuk
membuat integral dalam (5.110) penurut.
Dalam membahas gerak siklotron di atas kita telah mengabaikan efek tabrakan.
Tentu saja jika ini gerak siklotron harus diamati sama sekali, elektron harus
menyelesaikan sebagian besar dari orbit selama satu kali tabrakan yang
.
Hal ini memerlukan penggunaan sampel yang sangat murni pada suhu rendah di
bawah medan magnet yang sangat kuat.
Efek ruang
Ketika kami sedang mendiskusikan efek lorong dalam model elektron bebas kami
menemukan bahwa ruang konstan diberikan oleh
(5.111)
Dimana
adalah konsentrasi elektron. Tanda negatif ini disebabkan oleh muatan
negatif dari elektron. Perlakuan umum efek aula untuk elektron Bloch menjadi
sangat rumit untuk FS sewenang-wenang, memerlukan upaya yang cukup
matematis. Namun, kami dapat memperoleh beberapa hasil penting cukup mudah.
Misalkan lubang hanya hadir dalam sampel. Kemudian kita bisa menerapkan ke
lubang perlakuan yang sama digunakan untuk elektron dalam bagian 4.10 dan
akan mendapatkan aula konstan
(5.112)
Dimana R sekarang positif karena muatan positif pada lubang
adalah
konsentrasi lubang).
Sebenarnya di lubang logam tidak hadir dengan sendirinya selalu ada beberapa
elektron hadir. Jadi ketika dua band tumpang tindih dengan satu sama elektron,
lain yang hadir pada pita atas dan lubang dalam ekspresi lower.the untuk ruang
konstan ketika kedua elektron dan lubang yang ada secara bersamaan diberikan
oleh
Dimana
dan
merupakan kontribusi individu elektron dan lubang seperti
tertera di atas dan
(
dan
adalah konduktivitas elektron dan lubang
)
Persamaan (5,113) menunjukkan bahwa tanda aula R konstan mungkin baik
negatif atau positif tergantung pada apakah kontribusi elektron atau lubang
mendominasi. Jika kita mengambil
yang terjadi di logam, kemudian
dan tanda R ditentukan sepenuhnya oleh besaran relatif dari
konduktivitas
dan
. Jadi jika
, elektron memiliki massa kecil dan
seumur hidup lama kontribusi elektron mendominasi dan R adalah negatif. dan
ketika kondisi sebaliknya berlaku kontribusi lubang mendominasi dan R adalah
positif. Sekarang kita dapat mengerti mengapa beberapa logam Zn dan Cd
polyvalent-pameran ruang positif konstan
5.20 METODE EKSPERIMEN DALAM PENENTUAN STRUKTUR PITA
Sekarang kita diskusi beberapa teknik eksperimen yg digunakan untuk
menentukan struktur pita dalam metal. Sebagai contoh, bagaimana fisikawan
menentukan energi Fermi dalam tabel 4.1, atau permukaan fermi yg ditunjukan
pada gambar 5.26 untuk Cu dan gambar 5.30 untuk jadi apa? bidang fisika padat
ini adalah satu lebar dan telah berkembang dengan pesat. Karena itu diskusi kita
di sini akan lebih samar, meninggalkan itu ke pembaca untuk mengejar subjek
secara lebih rinci oleh Pengkelasan dalam bibliografi.
Kita dapat menentukan energi fermi oleh metode soft x-ray emission.Saat logam
ditembak oleh berkas e- energi tinggi, elektron dari kulit K tidak terkunci,
meninggalkan tempat kosong dibelakang. Elektron pada pita valensi sekarang
bergerak untuk mengisi lowongan ini, mengalami transisi ke bawah, seperti
ditunjukan pada gambar 5.43 (a).
Emisi foton saat transisi, biasanya menetap di daerah soft x-ray – kira-kira 200 eV
– dicatat dan energi mereka diukur.
Intensitas spektrum sinar x sama baik dengan angka energi untuk beberapa logam.
Saat kulit K sangat sempit, hampir sampai ke titik tingkat diskrit. Angka lebarnya
sepenuhnya disebabkan penyebaran zat yang diduduki pada pita valensi.
Mari kita sekarang beralih ke penentuan FS dan membahas salah satu metode
yang umum digunakan: teknik Azbel-Kaner cyclotron resonance (AKCR). Semi
tak terbatas pelat logam ditempatkan dalam medan magnet statis yang kuat Bo,
yang sejajar dengan permukaan (gbr. 5.44).
Akibatnya, elektron dalam logam mulai melaksanakan gerakan siklotron, dengan
frekuensi siklotron w. Sekarang sebuah alternatif sinyal elektromagnetik dari
frekuensi w, sirkuler terpolarisasi dalam arah searah jarum jam, diperbolehkan
untuk perjalanan sejajar dengan permukaan dan sepanjang arah medan statis Bo.
Sinyal ini menembus logam ini hanya untuk sebagian kecil, sama dengan
kedalaman kulit (lihat section 4.11), dan begitu juga terbatas pada jarak pendek
dari permukaan. Hanya elektron di daerah ini dipengaruhi oleh sinyal.
Elektron dekat dengan permukaan merasakan medan sinyal dan menyerap energi
darinya. Penyerapan ini adalah yg terbaik pada kondisi...
ω = ωc
(pers.
5.114)
Statis, karena kemudian elektron tetap dalam fase dengan bidang sinyal sepanjang
siklus.ini adalah kondisi resonansi.
selama ia bagian dari siklus, elektron sebenarnya menembus logam di luar
kedalaman kulit, di mana medan sinyal hilang. Kondisi resonansi masih statis
asalkan saat elektron kembali ke daerah permukaan, ia kembali berada di fase
dengan medan. Oleh karena itu, pada umumnya kondisi resonansi adalah...
ω = Iωc
(pers.
5.115)
Dimana l = 1, 2, 3,.., di semua harmonisasi dari frekuensi siklotron wc. AKCR
untuk Cu ditunjukan pada gambar 5.45. (biasanya frekuensi w tetap dan medan
bervariasi sampai kondisi resonansi tetap.)
Tidak hanya metode yang mampu menentukan ωc, (dan karenanya m* massa
efektif), tetapi juga bentuk aktual dari FS. Pada umumnya, elektron berbeda
daerah pada permukaan mempunyai perbedaan frekuensi siklotron, tapi frekuensi
yang paling diucapkan dalam penyerapan adalah frekuensi yang sesuai untuk orbit
ekstrim, dimana FS yg melintang tegak lurus dengan Bo paling besar atau paling
kecil. Karena itu, dengan memvariasikan orientasi Bo, seseorang dapat mengukur
bagian ekstrim di berbagai arah dan merekonstruksi FS.
Eksperimen biasanya ditampilkan pada temperatur rendah, yaitu T = 4 K, pada
sempel murni, dan pada medan yg sangat kuat sekitar 100 kG. Kondisi ini, waktu
t tabrakan cukup panjang, dan frekuensi siklotron ωc cukup tinggi, jadi kondisi
medan yg tinggi ωc ԏ >> 1 tetap. Pada batas ini, mengeksekusi siklus elektron
banyak dalam waktu tabrakan tunggal, yang mengarah ke resonansi, tajam
diselesaikan dengan baik. frekuensi ωc biasanya jatuh dalam kisaran microwave.
Teknik Optical Ultraviolet juga digunakan dalam penentuan struktur ikat. Gambar
5.46 menunjukan prinsip metodenya. Saat berkas sinar melanggar ke logam,
elektron tereksitasi dari bawah level fermi ke tingkat pita selanjutnya yg lebih
tinggi. Pita di dalam dapat diamati dengan cara optik - teknik reflektansi dan
penyerapan, yang memberikan informasi mengenai bentuk ikatan energi. dalam
kasus ini, 2 pita yang terlibat secara bersamaan, dan hasilnya tidak dapat
dinyatakan dalam satu pita masing-masing secara terpisah. Tapi jika bentuk salah
satu diketahui, bentuk yang lain mungkin dapat ditentukan. Untuk diskusi lebih
jauh dari sifat optik logam di daerah ultraviolet – yg di mana frekuensi terjadi
untuk dibiarkan dalam kasus hampir semua logam – lihat section 8.9
5.21 TEORI LIMIT DARI PITA; BAHAN INSULATOR TRANSISI
Sejauh ini pada chapter ini kita telah mendasari diskusi kita sepenuhnya pada yg
selanjutnya disebut model ikatan pada padatan. Model ini sudah nilai luar biasa
bagi kita, ia mampu menjelaskan semua sifat yang diamati logam dan merupakan
dasar dari sifat semi konduktor yang akan dibahas dalam bab 6 dan 7. namun
model ini memiliki keterbatasan yang sekarang ingin kita periksa.
Mempertimbangkan, misalnya, kasus Na. zat ini adalah konduktor karena ikatan
3s hanya sebagian diisi - setengah penuh, tepatnya. Misalkan kita menyebabkan
Na untuk memperluas dengan beberapa cara, sehingga kisi konstan bisa
ditingkatkan secara sewenang-wenang. akankah materi kemudian tetap konduktor
untuk setiap nilai sewenang-wenang dari nilai a? jawabannya harus ya, jika ada
yang percaya model pita, karena tanpa memperhatikan dari nilai a, pita 3s akan
selalu setengah penuh. benar (model memprediksikan lebih lanjut) bahwa o
konduktivitas penurunan sebagai peningkatan, tetapi penurunan secara bertahap.
Pada kenyataannya, bagaimanapun, ini tidak benar. seperti a meningkat, nilai
kritis ac yang dicapai di mana konduktivitas turun menjadi nol tiba-tiba, memberi
padatan sebuah isolator, dan itu tetap jadi untuk semua nilai a > ac. sehingga untuk
kisi besar cukup konstan, logam berubah menjadi isolator, dan kita berbicara
tentang logam - transisi isolator (juga dikenal sebagai transisi Mott).
Untuk menjelaskan transisi ini, kita butuh memanggil kembali konsep-konsep
fundamental yang mendasari teori pita. dalam teori ini, elektron Bloch
diasumsikan terdelokalisasi, memperluas seluruh kristal, dan inilah delokalisasi
yang bertanggung jawab untuk konduktivitas logam. sebagai partikel
terdelokalisasi, elektron Bloch gesekan menghabiskan waktu nya (1 / N,
tepatnya), di setiap atom. interaksi antara berbagai elektron Bloch diperhitungkan
hanya dalam yaitu, maner rata-rata, interaksi antara elektron individu diabaikan.
Namun, a sebagai suatu peningkatan, lebar pita berkurang (ingat model TB,
bagian 5.8), sampai menjadi sangat kecil di cukup besar a. dalam kasus ini, model
ikatan rusak karena memungkinkan adanya dua atau lebih elektron di lokasi kisi
yang sama, yang tidak bisa terjadi karena tolakan coulomb antara elektron. ketika
pita yang lebar, ini tidak serius, karena elektron dapat menyesuaikan kembali
energi kinetik mereka untuk mengkompensasi peningkatan energi Coulomb
potensial. tetapi untuk sebuah ikatan sempit energi kenetic adalah, saat terbaik,
cukup kecil, dan penyesuaian ini tidak mungkin berlaku, untuk sangat besar, maka
orbital elektronik yang tepat dalam kristal bukan dari jenis Bloch. mereka
dilokalisasi orbital orbital berpusat di sekitar sisi masing-masing, yang
memperkecil energi coulomb yg besar. karena orbital dilokalisasi, seperti dalam
kasus atom-atom bebas, konduktivitas lenyap, seperti yang digambarkan dalam
gambar catatan bahwa kesimpulan di atas berlaku meskipun masih tingkat energi
membentuk sebuah pita, dan meskipun pita hanya setengah penuh. poinnya adalah
bahwa orbital elektronik menjadi lokal, dan karenanya nonconducting.
Transisi logam-isolator telah diamati di VO2 (oksida vanadium) dan bahan oxited
lainnya. meskipun VO2 biasanya isolator, itu berubah menjadi bahan logam pada
tekanan cukup tinggi.