1. Nilai Sesaat, Nilai Maksimum dan Nilai Efektif Pada Bab 3 telah

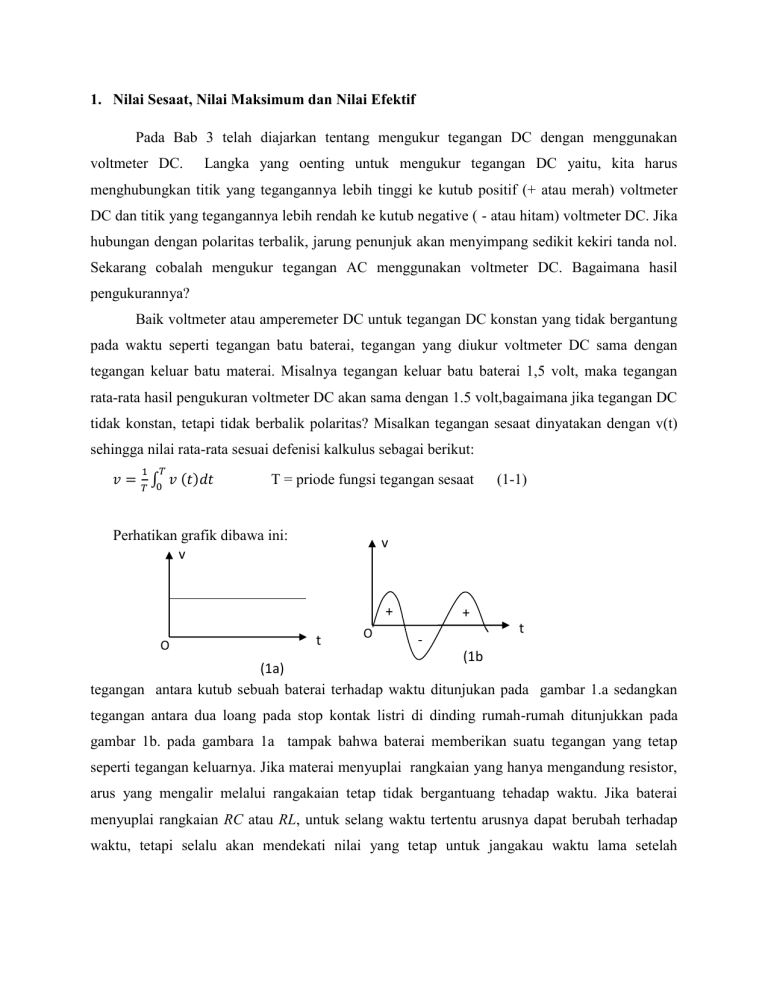
1. Nilai Sesaat, Nilai Maksimum dan Nilai Efektif
Pada Bab 3 telah diajarkan tentang mengukur tegangan DC dengan menggunakan
voltmeter DC.
Langka yang oenting untuk mengukur tegangan DC yaitu, kita harus
menghubungkan titik yang tegangannya lebih tinggi ke kutub positif (+ atau merah) voltmeter
DC dan titik yang tegangannya lebih rendah ke kutub negative ( - atau hitam) voltmeter DC. Jika
hubungan dengan polaritas terbalik, jarung penunjuk akan menyimpang sedikit kekiri tanda nol.
Sekarang cobalah mengukur tegangan AC menggunakan voltmeter DC. Bagaimana hasil
pengukurannya?
Baik voltmeter atau amperemeter DC untuk tegangan DC konstan yang tidak bergantung
pada waktu seperti tegangan batu baterai, tegangan yang diukur voltmeter DC sama dengan
tegangan keluar batu materai. Misalnya tegangan keluar batu baterai 1,5 volt, maka tegangan
rata-rata hasil pengukuran voltmeter DC akan sama dengan 1.5 volt,bagaimana jika tegangan DC
tidak konstan, tetapi tidak berbalik polaritas? Misalkan tegangan sesaat dinyatakan dengan v(t)
sehingga nilai rata-rata sesuai defenisi kalkulus sebagai berikut:
( )
∫
T = priode fungsi tegangan sesaat
Perhatikan grafik dibawa ini:
v
v
+
O
(1-1)
t
O
+
-
t
(1b
(1a)
)
tegangan antara kutub sebuah baterai terhadap waktu ditunjukan pada gambar 1.a sedangkan
tegangan antara dua loang pada stop kontak listri di dinding rumah-rumah ditunjukkan pada
gambar 1b. pada gambara 1a tampak bahwa baterai memberikan suatu tegangan yang tetap
seperti tegangan keluarnya. Jika materai menyuplai rangkaian yang hanya mengandung resistor,
arus yang mengalir melalui rangakaian tetap tidak bergantuang tehadap waktu. Jika baterai
menyuplai rangkaian RC atau RL, untuk selang waktu tertentu arusnya dapat berubah terhadap
waktu, tetapi selalu akan mendekati nilai yang tetap untuk jangakau waktu lama setelah
membuka atau menutup sakalar. Seperti yang anda pelajarai bahwa arus listrik yang hanya
mengalir satu arah disebut arus searah (direct curren disingkat DC).
Pada gambar 1b, tampak bahwa stop kontak di dinding rumah memberikan tegangan
yang berubah terhadap waktu secara sinusoidal dengan periode waktu tertentu. Tampak juga
bahwa tegangan sinusoidal ini dapat berbalik polaritas dari positif ke negatif atau sebaliknya
setelah jangkauan waktu tertentu secara periodik. Tegangan yang polaritasnya bergantian positif
dan negatif setiap jangkauan waktu tertentu disebut tegangan bolak-balik (tegangan AC) arus
yang dihasilkan sumber tegangan ini pun arahnya senantiasa bergantian perhatikan gambar
berikut ini:
i
i
Gambar 1c; yakni setiap setengan
siklus, polaritas tegangan erganti
positif dan negatif sehingga
menghasilkan arus yang senantiasa
berbalik arah secara priodik
i
i
(2c)
Setengan siklus ketika bagian atas polaritaspositif, arus listrik dalam rangkaian mengalir searah
jarum jam (ditunjukkan oleh garis utuh)
yang disebut sebagai arus maju. Setengan siklus
berikutnya, bagian arus berpolaritas negative sehingga arus listrik berbalik arah, yaitu mengalir
berlawanan arah jarum jam (mundur). Seterusnya berung kembali secara periodic. Arus maju dan
mundur yang terjadi secara periodic ini disebut arus bolak balik di singkat AC. Arus AC selalu
berubah arah secara periodic sehingga untuk memasang amperemeter AC atau voltmeter AC
anda tidak perlu memperhatikan polaritas titi mana pada rangkaian yang tegangannya leih
positif, s eperti ketika anda menhubungkan meter DC pada rangkaian.
Kurva yang kita peroleh ketika menggambarkan tegangan yang digambarkan stop kontak
di dinding rumah kita adalah tegangan AC berbentuk sinusoidal ) perhatikan gambar 1b)
tegangan ini pun akan menghasilkan arus AC yang juga berbentuk sinusoidal (gambar 3a). Im
sebagai kuat arus maksimum atau kuat arus puncak, i sebagai kuat arus sesaat dan T periode
kurva dalam satu siklus.
Kurva merupakan fungsi periodic sehingga untuk memudahkan kita, maka senut saja
kurva sinusoidal ini seagai gelombang sinusoidal.
Alat ukur DC mengukur kat arus atau tegangan rata-rata yang secara matematis
dirumuskan oleh persamaan (1a). Polaritas kuat arus a tau tegangan DC sesaat hanya dapat
positif saja atau negative saja (tidak dapat berbalik dari positif ke negates, atau sebaliknya),
sehingga nilai rata-ratanya tidak mungkin nol. Apakah nilai dan tegangan dan arus AC juga
dapat ditampilkan oleh nilai rata-rata seperti pada nilai tegangan dan arus DC?
Perhatikan gambar 7.3a dalam sau siklus gelomang, setengah siklus (0 ≤ θ ≤ π ) kurva
berada di sumbu θ, yakni bagian positif (daerah yang diasir) adapun setengah siklus kemudian (π
≤ θ ≤ 2π ) kurva berada di bawa simbu θ, yakni bagian negative(daerah yang diarsir). Tampak
bahwa luas bagian positif sama dengan bagian negative sehingga nilai rata-rata arus AC dalam
satu siklus adalah nol. Oleh karena itu, arus AC tidak layak jika dinyatakan dengan nilai ratarata seperti pada DC.
Bagaimana kita nyatakan kuat arus atau tegangan AC? Metode terbaik adalah
mengukurnya seperti untuk arus DC. Seperti anda ketahui daya yang dibuang dalam bentuk
panas(daya disipasi) pada peralatan listrik dengan hambatan R adalah
p = i2R.
(1-1)
untuk arus DC, nilai i adalah arus rata-rata, seperi anda telah ketahui bahwa nila arus rata-rata
untuk arus AC adalah nol sehingga daya disipasinya akan nol.
Hal ini tentu saja salah.
Bagainman jika arus searah AC, i = Im2 sin θ, ini kita kuadratkan, kemudian kita gambar
kurvanya. Kita peroleh fungsi i2 = Im sin2 θ. Kurva i2 selalu di atas sumbu θ sehigga jelas harga
rata-ratanya tidak nol seperti harga rata-rata i. supaya kita dapat mengukur AC s eperti arus DC
maka pakar listrik mengusulkan untuk menggunakan harga rata-rata i2 ini dan menarik akarnya,
yang disebut arus rms (singkatan dari roo mean square) yang berarti kara dari kuadrat rata-rata
atau Arus efektif ditilis (Im atau Ief)
Ief = √( )
(1-2)
Dengan demikian daya disipasi pada arus AC sekarang dapat dirumuskan seperti pada
arus DC dengan mengganti arus rata-rata i pada DC dengan arus efektif, Ief pada AC sebagai
berikut
p = Ief 2R.
(1-3)
arus efektif pada AC berperan sepertiarus rata-rata pada DC. Misalkan seperti kita mengatakan
nilai efektif arus AC adalah 4 A, ini berarti bahwa arus AC akan mendisipasidaya dalam bentuk
panas yang sama seperti arus DC ketika keduanya melalui hambatan R yang sama. Dengan
menggunakan definisi nilai rata-rata fungsi pada kalkulus, kita d engan mudah dapat menghitung
nilai efektif dari arus AC sinusoidal/
i = Im2 sin θ dimana i2 = Im sin2 θ
Ief = √( )
)
= √(
Perhatikan kurva pada gambar 3b. setiap selang π membentuk kurva berulang. Hal ini
berarti periode dari fungsi i2 = Im sin2 θ adalah θ = π. Sehingga menjadi
Ief = √ ∫ (
)
Selanjutnya berdiskusilah dengan kelompokmu dan hitunglah integral di ruas kanan
sampai tuntas seingga diperoleh arus efektif
Ief =
√
Berikut ini kita akan menurunkan nilai efektif arus DC dengan menyamakan daya
dan p = Ief 2R. dengan ( )
disipasi yang diperoleh dari p = ( )
R.
arus sinudoidal dapat kit abaca dari grafik
terhadap θ pada gambar 7.3b. jika kita tarik garis
mendatar patah-patah dengan i2 =
untuk
kita dapatkan bahwa luas bagian di atas garis patah-patah
sama dengan luas bagian di bawah garis patah-patah. Dengan demikian nilai rata-rata i2 sama
dengan
.
p=( )
p=
R
I2ef R =
I2ef =
R
R
√
I2ef =
Nilai efektif arus
Nilai efektif tegangan
Vef =
√
√
= 0,7071 Im
= 0.707 Vm
(1-4)
(1-5)