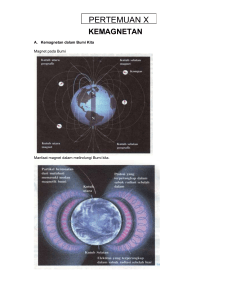
William Gilbert adalah orang pertama kali

MEDAN MAGNET
William Gilbert adalah orang pertama kali mengatakan bumi merupakan magnet yang
sangat besar. Pengetahuan tentang magnet bumi sangat penting untuk pelayaran, dan
untuk komunikasi massa yang akan datang. Dengan magnet para ilmuwan dapat pula
menciptakan alat-alat ukur listrik, dapat menyimpan partikel bermuatan berenergi tinggi
dan lain-lain, itulah sebabnya kita harus mempelajari magnet dengan serius dan
mendalam.
A. Pengertian Medan Magnet
Medan Magnet adalam suatu daerah atau area yang apabila dihadirkan benda-benda
magnet , muatan bergerak dan atau kawat berarus akan mendapat gaya magnet.
Contoh medan magnet yang paling mudah adalah ruangan di sekitar magnet batang
S
Jika diatasnya ditutup karton
dan ditaburui serbuk besi akan
nampak pola garis yang disebut
garis gaya magnet
U
Ket : Gambar magnet batang
Adanya pola garis tersebut membuktikan bahwa dalam medan magnet terdapat garis
khayal yang disebut ” garis gaya magnet”.
Untuk menyebutkan besar kecilnya medan magnet dalam suatu titik dinyatakan dalan
besaran : Kuat Medan Magnet/ Induksi Magnet ( B).
Kuat Medan Magnet/ Induksi Magnet ( B) merupakan besaran vektor dengan
perjanjian :
1. Arahnya merupakan garis singgung garis gaya magnet di titik tersebut.
2. Besarnya sebanding dengan kerapatan garis gaya manet dititik tersebut
Besar induksi magnet di luasan
A didefinisikan sebagai :

Luasan A

B=
A cos 
Dimana :
B = kuat medan
magnet
( Wb/m2 = Tesla)
 = jumlah garis gaya ( Wb)
 = sudut antara ggm dengan
normal bidang
Garis gaya magnet
B. Induksi Magnetik
1. Percobaan Oersted
Mari kita lakukan eksperimen sederhana dengan kompas, sebatang kawat dan
baterei / power supply.
 Tempatkan kompas di atas meja
 Tempatkan kawat yang telah dialiri arus dengan batu baterei di atasnya
Yang akan anda lihat adalah jarum kompas yang menyimpang. Kenapa jarum
kompas menyimpang ? Bagaimana jika arah arus listrik arahnya diubah ?
I=0
(a)
Kompas di bawah
penghantar
I
(b)
I
(c)
Kesimpulan :
a. Arus listrik menghasilkan medan magnet ( peristiwa timbulnya medan
magnet di sekitar kawat lurus disebut induksi magnetik )
b. Arah arus listrik mempengaruhi penyimpangan kompas ( arah putaran
garis gaya magnet)
c. Putaran garis gaya magnet mengikuti kaidah tangan kanan
Arah putaran ggm
2. Hukum Biot Savart
Berdasar eksperimennya Jean-Babtiste Biot dan Felix Savart merumuskan
secara matematis besarnya medan magnet di suatu titik di sekitar kawat
berarus listrik.
Jika dB adalah sumbangan / kontribusi induksi magnet pada titik P yang
ditimbulkan oleh elemen penghantar dl yang dialiri arus listrik I maka :
dB
dl

r
Arus (I)
dB
O
P
=
o I dl sin 
4
r2
dimana :
I = kuat arus listrik ( I)
dl = panjang elemen penghantar
o= permeabilitas hampa
= 4  X 10 -7 Wb/ A. M
 = sudut antara dldan r
Rumusan matematis pada Hukum Biot Savart tersebut dapat digunakan untuk
mencari induksi magnet di suatu titik akibat bermacam-macam bentuk kawat berarus
listrik.
B.1. Induksi Magnetik di sekitar penghantar lurus berarus
Apabila dialirkan arus listrik pada penghantar lurus yang menembus sebuah karton
yang ditaburi serbuk besi maka serbuk besi akan menunjukkan pola-pola garis gaya
magnet yang berbentuk lingkaran-lingkaran sepusat .
Tanda titik ()sering digunakan untuk menyatakan arah tegak lurus keluar bidang
gambar atau arah menuju pembaca. Tanda kali ( X ) menyatakan arah tegak lurus
masuk bidang gambar atau arah meninggalkan pembaca. Bagaimana cara menentukan
arah induksi magnet di kawat lurus berarus listrik ?
BA
BB

I
Arah put ggm
 BD
X BC

X
Ingat : arah induksi magnet di suatu titik merupakan garis singgung garis gaya
magnet di titik tersebut.
Besarnya induksi magnet yang ditimbulkan oleh penghantar lurus berarus diturunkan
dari Hukum Biot Savart.
Perhatikan gambar di bawah ini :
2
Sin  =
a
O

-l
dl
a
r = a cosec …….(a)
r
Cotg  = -l / a
l = a cosec 2  d…(b)
Jika (a) dan (b) digabung dalam pers bit
Savart diperoleh :

r
dB
=
= 1
o I dl sin 
4
r2
I
dB
dB
=
=
o I a cosec 2  sin  d
4
a 2 cosec 2 
o I sin  d
4 a
Untuk memperoleh Bp dilakukan langkah integral dengan batas bawah 1 dan batas
atas  2 . maka akan diperoleh :
2
o I
Bp =
sin  d
4a
1
2
o
I
(-cos

o I (cos  1- cos 2 )
Bp =
1 =
4a
4a
Untuk 1 =  dan  2 = 180 -  maka
Bp =
o I
(cos  + cos )
4a
Berlaku
untuk
menentukan induksi magnet di
sekitar kawat lurus berarus I.
Persamaan 1
Contoh Soal :
P
Penghantar PQ yang panjangnya 4 m di beri arus 2 A ke
bawah . Hitunglah besar dan arah kuat medan magnetik di
titik R yang berjarak 2 m dari kawat !
4m
R
Q
2m
Jawab :
a. arah B di titik R sesuai kaidah tangan kanan Oersted adalah masuk bidang
gambar .
b. Untuk menentukan besar B R ,sebelumnya ditentukan lebih dulu a,  dan  .
P
Diketahui :

A = 2 m , cos  = 4/5 dan cos  = cos 90 
4m
Jawab :

Q
R
Bp =
o I
(cos  + cos )
4a
a=2m
4 . 10 -7 . 2
Bp =
4 . 2
(4/5 + 0 ) = 0,8  . 10 -7 Tesla
Tugas 1 : Hitunglah besar dan arah kuat medan magnetik di titik O !
A
1.
B
ABC adalah penghantar lurus berarus 10A .
Jika AB= BC = 4 cm hitung besar dan arah
induksi magnet di titik O.
O
I= 10A
C
2. Hitung besar dan arah induksi magnet titik P di sekiar kawat berbentuk U berikut !
Q
R
Jika diketahui QR = 6 3 m SR =
12 m dan P tengah-tengah QT.
P
I=2A

T
S
Kasus khusus pada induksi magnet di sekitar penghantar lurus berarus listrik.
Untuk kawat yang panjangnya tak berhingga dibandingkan dengan jarak titik yang
akan tentukan induksi magnet dengan kawat maka :
 = 0
1.
 = 0
o I ( 1 + 1)
Bp =
4a
P
 = 90
P ditengah-tengah cos  =
cos  = 1
 = 0
2.
Bp =
3. P

 = 0
oI
2a
P di pinggir kawat cos  =
0 cos  = 1
P
 = 180
=
oI
4a
P hampir segaris kawat
cos  = - 1, cos  = 1
Bp = 0
B.2 Medan magnet di Sumbu Kawat Melingkar Berarus Listrik
Perhatikan gambar kawat melingkar berikur yang berjari-jari a berarus I berikut.
dl
a
I
dB cos 
r

O = pusat kawat melingkar
a = jari-jari kawat
P = titik di sembarang kawat
berjarak x dari pusat kawat
dB
P
dB sin 
O
Setiap dl akan menyumbang kemagnetan masing-masing dB terhadap titik P,
besar sama tetapi arah berbeda. Hal ini menyebabkan vektor dl cos  akan saling
meniadakan sehingga arah dan besar induksi magnet di titik P tergantung pada dB
sin . Pada kasus seperti gambar maka Bp berarah ke kanan.
Untuk menentukan arah kuat medan magnet di P dapat ditentukan dengan kaidah
tangan kanan sebagai berikut :
BP
B
Putaran I
I
Gambar cara menentukan arah kuat medan magnet di sumbu kawat melingkar
C. Gaya Lorentz
D.
E.