140310180043 Darling Josua Manalu Laporan Awal Modul 12

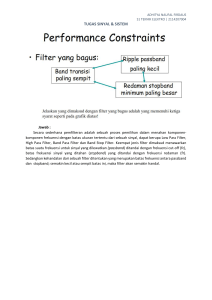
DESAIN FILTER FIR
LAPORAN PRAKTIKUM
DARLING JOSUA MANALU
140310180043
UNIVERSITAS PADJADJARAN
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
PROGRAM STUDI FISIKA
2021
1
2
DAFTAR ISI
DAFTAR ISI ................................................................................................................. 2
BAB 1 PENDAHULUAN ............................................................................................ 3
1.1 Latar Belakang ................................................................................................... 3
1.2 Tujuan ................................................................................................................ 3
BAB 2 TINJAUAN PUSTAKA ................................................................................... 4
2.1 Filter Digital ....................................................................................................... 4
2.2 Elemen Dasar Filter Digital .............................................................................. 10
2.3 Dasar-dasar Perancangan Filter........................................................................ 11
2.4 Sifat-sifat Filter FIR Fasa Linier ...................................................................... 13
2.5 Teknik Mendesain Window ............................................................................. 14
2.6 Teknik Desain Sampling Frekuensi ................................................................. 16
BAB 3 METODE PENELITIAN................................................................................ 18
3.1 Rencana Perancangan Algoritma Penelitian .................................................... 18
3.2 Alat-alat Percobaan .......................................................................................... 19
3.3 Prosedur Percobaan ........................................................................................... 19
DAFTAR PUSTAKA ................................................................................................. 20
3
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Filter merupakan suatu perangkat yang menghilangkan bagian dari sinyal yang
tidak di inginkan. Filter digunakan untuk menglewatkan atau meredam sinyal yang di
inginkan dari sinyal noise. Seiring dengan perkembangan teknologi yang berbasis
digital, teknik desain filter pun mengalami kemajuan pesat. Ada beberapa teknik desain
yang dapat dilakukan, masing-masing memiliki kelebihan di dalam beberapa aplikasi
tertentu. Salah satu teknik desain filter dimaksud adalah teknik desain filter dengan
finite impulse response (FIR), yang dianalisis dengan teknik windowing. Desain filter
digital dengan menggunakan teknik windowing adalah merupakan salah satu alternatif
pilihan terbaik bagi para perancang filter digital. Teknik desain ini secara luas telah
digunakan dalam desain filter digital.
1.2 Tujuan
1. Mengenal algoritma dasar filter digital
2. Mampu mendesain filter FIR dengan spesifikasi yang ditentukan
3. Memahami konsep filter digital dan Analisa spektrum
BAB 2
TINJAUAN PUSTAKA
2.1 Filter Digital
Struktur filter digital ditentukan dari persamaan beda atau fungsi sistem yang
disebut Direct Form I. Sebuah pandangan alternatif dari hasil persamaan yang sama
disebut Direct form II. Struktur Filter digital sebagai cascade dan kombinasi paralel
dari komponen orde kedua.
1.
Persamaan Sistem
Persamaan yang melukiskan hubungan masukan/keluaran dalam waktu dan
domain transformasi-z, adalah sebagai berikut:
Dalam domain waktu:
Persamaan beda:
Dalam domain transformasi-z, fungsi sistem dapat dieksresikan ke dalam dua
bentuk. Pertama adalah penjumlahan
2.
Filter Catagories
Filter digital sering dikatagorikan baik oleh durasi tanggapan unit-sample atau
dari strukturnya. Ketika sebuah filter menghasilkan tanggapan unit-sample
dengan durasi tak terhingga (infinite), maka disebut infinite impulse response
(IIR) filter. Jika tapis digital mempunyai tanggapan unit-sample dengan durasi
finite, maka disebut finite impulse response (FIR). Klasifikasi filter digital juga
dapat berdasarkan struktur tapis/filter. Secara umum, keluaran filter dapat
berupa sebuah fungsi yang akan datang, sekarang, dan masukan yang lalu. Jika
keluaran adalah sebuah fungsi keluaran yang dulu, maka mekanisme umpan-
4
5
balik atau recursive atau disebut recursive filter. Tapis recursive dapat dikenali
dari persamaan, koefisien ak dengan 1 k  M, dari pers (2) dan (3) adalah tidak
nol, dan sedikitnya koefisien dk untuk 1 k  M pada persamaan (4) tidak nol.
Jika nilai keluaran tapis adalah fungsi yang hanya nilai runtun masukan, disebut
nonrecursive filter. Atau dapat dengan mudah dikenali dengan persamaan, ak =
0 pers(2) dan (3) atau dk = 0 pada pers(4). Untuk semua k. Semua nilai pole
dari tapis nonrecursive adalah pada z = 0 adau z = ∞.
3.
Direct Form Tipe 1 dan 2
Fungsi karakteristik sistem IIR dapat dilihat sebagai dua sistem secara kaskade,
yaitu:
dimana H1(z) terdiri atas zero dari H(z) dan H2(z) terdiri atas pole dari H(z),
Persamaan di atas dapat diwujudkan dalam struktur IIR Direct Form I sebagai
berikut:
6
Dalam pemrosesan sinyal, fungsi filter adalah untuk menghapus bagian yang tidak
diinginkan dari sinyal, seperti noise, atau untuk mengambil bagian sinyal yang
bermanfaat, seperti komponen-komponen yang berada dalam rentang frekuensi
tertentu.
yang merupakan kascade dari sistem non-rekursif :
dan sistem rekursif :
7
Jika semua filter all-pole H2(z) diletakkan sebelum filter all-zero H1(z) diperoleh
struktur yang lebih compact yang dinamakan struktur Direct Form II seperti pada
gambar berikut :
Struktur di atas dapat dinyatakan dalam persamaan perbedaan sebagai berikut:
•
Struktur di atas dapat dinyatakan dalam persamaan perbedaan sebagai
berikut:
•
untuk sistem all-zero dimana w(n) sebagai inputnya:
8
Persamaan di atas hanya mengandung delay pada deretan {w(n)} sehingga
hanya sebuah jalur delay tunggal atau satu set lokasi memori tunggal yang diperlukan
untuk menyimpan nilai {(n)}sebelumnya. Jadi, struktur IIR Direct Form 2 tersebut
hanya membutuhkan M + N + 1 perkalian, M+N penjumlahan dan nilai maksimum
{M,N}lokasi memori. Karena realisasi direct form 2 meminimasi jumlah lokasi
memori, maka struktur tersebut dikatakan bersifat canonic. Kedua struktur di atas
dikatakan direct form sebab diperoleh secara langsung dari fungsi sistem H(z) tanpa
penyusunan kembali H(z) tersebut. Namun, keduanya sangat sensitif terhadap
parameter kuantisasi dan oleh karenanya tidak direkomendasikan dalam aplikasi
prakteknya.
Jenis filter
Gambar 2.1. Blok diagram filter (Tyson, 2013)
Ada dua jenis filter, yaitu analog dan digital. Filter analog adalah filter yang
menggunakan komponen sirkuit analog seperti resistor, kapasitor dan penguat
operasional (Op Amp) sesuai fungsi filter yang diinginkan. Ada teknik standar yang
sudah baik untuk mendesain rangkaian filter analog untuk kebutuhan tertentu. Pada
semua stage, sinyal yang difilter adalah tegangan atau arus listrik yang merupakan
sinyal analog.
Filter digital adalah tapis yang menggunakan prosesor digital untuk melakukan
perhitungan numerik pada nilai-niai sampel dari sinyal. Prosesor yang digunakan dapat
berupa PC atau DSP (Digital Signal Processor). Untuk pengunaan filter digital, input
sinyal analog harus didigitalisasi menggunakan ADC (Analog to Digital Converter).
Dari ADC akan dihasilkan data-data biner yang kemudian akan diproses oleh filter
digital (Tyson, 2013). Berikut adalah perbandingan antara filter analog
9
Tabel 2.1. Perbandingan Filter Digital dan Analog (Element 14, 2019)
Digital Filters
Analog Filters
High Accuracy
Less Accuracy (Component Tolerances)
Linear Phase (FIR Filters)
Non-Linear Phase
No Drift Due to Component Variations
Drift Due to Component Variations
Flexible, Adaptive Filtering Possible
Adaptive Filters Difficult
Easy to Simulate and Design
Difficult to Simulate and Design
Computation Must be Completed in
Analog Filters Required at High
Sampling Period (Limits Real Time
Frequencies and for Anti-Aliasing
Operation)
Filters
Requires High Performance ADC, DAC
No ADC, DAC or DSP Required
and DSP
Sinyal analog input harus disampling dan didigitalisasi menggunakan ADC.
Hasilnya yang berupa
angka biner
yang
merepresentasikan
sinyal
input
ditransfer/disalurkan ke prosesor, dimana sinyal digital tersebut membawa kalkulasi
numerik. Kalkulasi ini secara khusus melibatkan pelipatgandaan nilai input dengan
konstan dan menjumlahkan hasilnya. Jika dibutuhkan, hasil dari kalkulasi ini yaitu
yang merepresentasikan sinyal tertapis, dimasukkan kedalam DAC untuk
mengembalikan ke sinyal analog lagi (Tyson, 2013)
10
Gambar 2.2. Blok Diagram Sinyal Analog yang Ditapis Filter Digital
Filter digital dibagi dua, yaitu Finite Impulse Response (FIR) dan Infinite Impulse
Response (IIR).
2.2 Elemen Dasar Filter Digital
Elemen dasar pada filter digital berfungsi untuk menggambarkan struktur dasar
dari filter digital. Ada 3 elemen dasar pada struktur filter digital yaitu:
•
Adder (Penjumlah)
Elemen ini memiliki dua input dan satu output. Kedua input ini kemudian
akan dijumlahkan dan menghasilkan output baru.
Gambar 2.3. Elemen Penjumlah
•
Multiplier (Pengali)
Elemen ini memiliki satu input dan satu output. Input akan dikali dengan
sebuah konstanta gain (penguat) untuk menghasilkan output yang baru.
Elemen multiplier ini harus cepat dan memiliki nilai presisi (jumlah bit)
untuk mendukung hasil yang diinginkan.
11
Gambar 2.4. Elemen Pengali
•
Delay (Penunda)
Elemen ini memungkinkan untuk mengakses nilai-nilai sebelum atau
sesudah sekuen. Delay dibagi menjadi dua, yaitu delay positif (untuk
menyimpan sekuen waktu berikutnya) dan delay negatif (untuk
menyimpan sekuen waktu sebelumnya)
Gambar 2.5. Elemen Delay Negatif
Gambar 1.6. Elemen Delay Positif
2.3 Dasar-dasar Perancangan Filter
Perancangan filter dilakukan melalui tiga tahap yaitu:
1. Menentukan spesifikasi filter yang akan dirancang seperti jenis, respon
amplitude dan frekuensi sampling.
2. Menghitung koefisien filter digital h(n), supaya dapat memenuhi spesifikasi
seperti yang diinginkan. Tentunya koefisiennya sudah diuji responnya dalam
bentuk respon frekuensi.
3. Melakukan realisasi filter kedalam bentuk struktur yang sesuai menggunakan
sistem diskrit dengan fungsi delay dalam variable z-1.
12
4. Menyesuaikan sistem yang dirancang kedalam bentuk hardware, menyangkut
wordlength untuk merepresentasikan koefisien filter yang sudah dihitung.
(Pangaribuan, 2015)
Spesifikasi besaran diberikan dalam dua cara. Pendekatan pertama disebut
absolute specification, yang memberikan seperangkat syarat untuk fungsi respon
besaran |𝐻(𝑒 𝑗𝑤 )|. Pendekatan yang ke-2 disebut relative specifications, yang
memberikan syarat dalam decibels (dB), diberikan oleh
𝑑𝐵 𝑠𝑐𝑎𝑙𝑒 = −20 log10
|𝐻(𝑒 𝑗𝑤 )𝑚𝑎𝑥 |
|𝐻(𝑒 𝑗𝑤 )|
≥0
(2.1)
a. Absolute Specifications
Ciri khas dari absolute specification dari lowpass filter:
1.
Pita [0,ωp] disebut passband, dan δp adalah ripple atau noise yang
dapat diterima sebagai respon passband ideal (khusus ≤ 0.1 dB)
2.
Pita [ωs,π] disebut stopband, dan δs adalah ripple atau noise yang dapat
diterima sebagai respon stopband yang ideal (umumnya ≤ 0.001 =-60
dB).
3.
Pita [ωp, ωs] disebut transition band atau transition width dengan
besarnya ωs-ωp. (DSP Related, 2017)
b. Relative (dB) Specifications
Ciri khas dari relative specification dari lowpass filter:
1.
Rp merupakan ripple passband dalam dB
1−𝛿𝑝
𝑅𝑝 = −20 log10 1+𝛿 > 0 (≈ 0)
(2.2)
𝑠
2.
As merupakan stopband attenuation dalam dB
𝛿
𝐴𝑠 = −20 log10 1+𝛿𝑠 > 0 (≫ 1)
𝑝
(2.3)
13
2.4 Sifat-sifat Filter FIR Fasa Linier
Filter Finite Impulse Response (FIR) merupakan sistem open loop atau sistem nonrecursive. Fasa linier mengacu pada kondisi dimana respons fase dari filter adalah
fungsi frekuensi linier (garis lurus tidak termasuk pembungkus fase pada +/- 180
derajat). Ini menghasilkan penundaan melalui filter yang sama di semua frekuensi.
Oleh karena itu, filter tidak menyebabkan “fase distorsi” atau “keterlambatan distorsi”.
Kurangnya distorsi fasa/penundaan dapat menjadi keuntungan penting dari filter FIR
atas IIR dan filter analog dalam sistem tertentu, misalnya dalam modem data digital.
(DSP Guru, 2018)
1.
Respon impuls
Kita menentukan suatu Batasan fasa linier
< 𝐻(𝑒 𝑗𝜔 ) = −𝛼𝜔, −𝜋 < 𝜔 < 𝜋
(2.4)
dengan α adalah constant phase delay. Kita ketahui bahwa h(n) adalah simetri
yaitu
ℎ(𝑛) = ℎ(𝑀 − 1 − 𝑛), 0 ≤ 𝑛 ≤ (𝑀 − 1) dengan 𝛼 =
𝑀−1
2
(2.5)
Sehingga h(n) adalah simetri diseputar α yang merupakan indeks simetri. Terdapat
dua kemungkinan tipe simetri:
M odd : pada kasus ini α = (M-1)/2 adalah bilangan bulat.
M even : pada kasus ini α = (M-1)/2 adalah bilangan bulat
Kita juga mempunyai tipe ke-2 dari filter FIR fasa linier jika memerlukan
respon fasa <H(𝑒 𝑗𝜔 ) memenuhi kondisi
<H(𝑒 𝑗𝜔 ) = 𝛽 − 𝛼𝜔
(2.6)
dengan garis lurus tetapi tidak melalui titik asal. Pada kasus ini α tidak merupakan
konstanta delay fasa tetapi
𝑑 < 𝐻(𝑒 𝑗𝜔 )
= −𝛼
𝑑𝜔
(2.7)
14
adalah konstanta yang merupakan delay kelompok (group). Oleh karena itu α
disebut constant group delay. Pada kasus α sebagai grup ini, frekuensi ditunda
pada suatu rate konstan. Tetapi beberapa frekuensi mungkin mendaatkan
penundaan yang lebih besar dan yang lainnya lebih kecil. Untuk tipe fasa linier ini
bisa dilihat bahwa
ℎ(𝑛) = −ℎ(𝑀 − 1 − 𝑛), 0 ≤ 𝑛 ≤ (𝑀 − 1); 𝛼 =
𝑀−1
𝜋
,𝛽 = ±
2
2
(2.6)
Ini berarti bahwa impuls h(n) adalah antisymmetric. Index simetri tetap α=(M-1)/2.
Kita sekali lagi mempunyai kemungkinan dua tipe yaitu M ganjil dan M genap
M odd : pada kasus ini α = (M-1)/2 adalah bilangan bulat.
M even : pada kasus ini α = (M-1)/2 adalah bilangan bulat
2.
Respon frekuensi
Ketika kasus simetri dan antisimetri dikombinasikan dengan M genap dan
ganjil, kita mendapatkan empat tipe filter FIR fasa linier. Fungsi respon frekuensi
untuk masing-masing tipe ini mempunyai ke khasan ekspresi dan bentuk. Kita
menuliskan H(ejω) sebagai
𝜋
𝐻(𝑒 𝑗𝜔 ) = 𝐻𝑟 (𝜔)𝑒 𝑗(𝛽−𝛼𝜔) : 𝛽 = ± 2 , 𝛼 =
𝑀−1
2
(2.7)
dengan Hr (ω) adalah fungsi respon amplitude dan bukan fungsi respon
besaran yang selalu positif, amplitude respon bisa positif dan negatif. Respon fasa
yang berkaitan dengan respon besaran adalah fungsi discontinuous, sementara
yang berkaitan dengan respon amplitude adalah fungsi continuous linear.
2.5 Teknik Mendesain Window
Jika dalam domain frekuensi fungsi filter terbatas, maka fungsi tersebut dalam
domain waktu adalah tak terbatas. Dalam domain frekuensi bahwa filter sifatnya adalah
terbatas yaitu hanya melalukan sinyal pada frekuensi tertentu, diinginkan fungsi sistem
dimaksud juga menjadi terbatas dengan filter yang memiliki panjang sebanyak h(n).
15
Oleh karena itu untuk membatasi panjang filter dalam domain waktu digunakanlah
metoda windowing.
Suatu filter ideal Hd (ejω) memiliki respon frekuensi dengan bentuk rectangular,
dikonvolusikan dengan sebuah window W(ejω) yang memiliki respon bukan
rectangular, tapi memperoleh respon filter H(ejω) (Pangaribuan, 2015).
Gambar 2.3. Respon Frekuensi Lowpass Filter Metoda Windowing (Pangaribuan,
2015)
Fungsi-fungsi window yang sering digunakan dalam desain filter digital adalah
sebagai berikut:
1.
Rectangular. Window rectangular mempunyai amplitude sama dengan besar
sama dengan satu untuk filter terbatas pada derajat N.
1,
𝜔𝑅 (𝑛) = {
0,
2.
0≤𝑛≤𝑁−1
𝑒𝑙𝑠ℎ𝑒𝑤ℎ𝑒𝑟𝑒
(2.8)
Batrlet. Window Bartlet mempunyai amplitude yang tidak sama besarnya dan
berbentuk segitiga, untuk filter terbatas pada derajat N.
2𝑛
,
𝑁−1
2𝑛
𝜔𝐻𝑎𝑛 (𝑛) =
2−
,
𝑁−1
{0,
3.
0≤𝑛≤
𝑁−1
2
𝑁−1
≤𝑛 ≤𝑁−1
2
𝑒𝑙𝑠𝑒𝑤ℎ𝑒𝑟𝑒
(2.9)
Hanning. Window Hanning mempunyai amplitude yang dibentuk oleh fungsi
cosinus, untuk filter terbatas pada derajat N.
(2.10)
16
{1 − cos [
𝜔𝐻𝑎𝑛 (𝑛) = {
2
2𝜋𝑛
𝑁 − 1]} ,
0,
4.
0≤𝑛 ≤𝑁−1
𝑒𝑙𝑠ℎ𝑒𝑤ℎ𝑒𝑟𝑒
Hamming, sama seperti Hanning namun berbeda pada matematisnya
𝜔𝐻𝑎𝑚
(𝑛) = {0.54 − 0.46 cos [
2𝜋𝑛
],
𝑁−1
0≤𝑛 ≤𝑁−1
0,
5.
𝑒𝑙𝑠ℎ𝑒𝑤ℎ𝑒𝑟𝑒
(2.11)
Blackman. Window ini mempunyai amplitude yang juga dibentuk oleh fungsi
cosinus, untuk filter terbatas pada derajat N
2𝜋𝑛
4𝜋𝑛
0.42
−
0.5
cos
[
]
+
0.08
cos[
],
𝜔𝐵𝑙 (𝑛) = {
𝑁−1
𝑁−1
0,
0≤𝑛≤𝑁−1
𝑒𝑙𝑠ℎ𝑒𝑤ℎ𝑒𝑟𝑒
(2.12)
Gambar 2.4. Respon Frekuensi dengan Windowing (Pangaribuan, 2015)
2.6 Teknik Desain Sampling Frekuensi
Pada pendekatan desain ini kita menggunakan fakta bahwa fungsi sistem H(z)
dapat ditentukan dari sampel H(k) dari frekuensi respon H(ejω). Selanjutnya, teknik
17
desain ini cocok sekali dengan struktur sampling frekuensi sebelumnya. Misalkan h(n)
adalah respon impuls dari filter FIR M-point, H(k) merupakan DFT M-point nya, dan
H(z) merupakan fungsi sistemnya.
ℎ(𝑛) = 𝐼𝐷𝐹𝑇 [𝐻(𝑘)]
Terdapat dua pendekatan desain pada pendekatan pertama, kita menggunakan ide
dasar harfiah dan tanpa pembatasan pendekatan error yaitu kita terima apapun error
yang kita dapatkan dari desain. Pendekatan ini disebut metode Naïve Design. Pada
pendekatan kedua kita mencoba untuk meminimalisasi kesalahan pada stopband
dengan memvariasikan nilai dari transisi sampel band. Ini menghasilkan desain yang
lebih baik dan disebut Optimum Design Method (Ingle & Proakis, 2012).
BAB 3
METODE PENELITIAN
3.1 Rencana Perancangan Algoritma Penelitian
Gambar 3.1 Diagram Alir secara umum modul XII
18
19
Gambar 3.2 Diagram Alir Praktikum Modul XII
3.2 Alat-alat Percobaan
1. Komputer/Laptop
2. Perangkat Lunak Matlab
3.3 Prosedur Percobaan
1. Membuka perangkat lunak Matlab yang ada di computer
2. Menuliskan listing fungsi sesuai dengan operasi yang ingin dilakukan didalam
M-File
3. Memasukkan fungsi filter, kemudian dengan menggunakan fungsi yang sudah
ada mengerjakan didalam command window
4. Menjalankan program
5. Mengamati hasil operasinya dan menganalisa
DAFTAR PUSTAKA
DSP
Guru,
2018.
Available
FIR
Filter
at:
Properties.
[Online]
https://dspguru.com/dsp/faqs/fir/properties/
[Accessed 26 March 2020].
DSP
Related,
2017.
Lowpass
Filter
Design
Specifications.
[Online]
Available
at:
https://www.dsprelated.com/freebooks/sasp/Lowpass_Filter_Design_Specificat
ions.html
[Accessed 26 March 2020].
Element
14,
2019.
Available
Digital
at:
Filters.
[Online]
https://sg.element14.com/
[Accessed 19 March 2020].
Ingle, V. K. & Proakis, J. G., 2012. Digital Signal Processing Using MATLAB.
Stamford, USA: Cengage Learning.
Pangaribuan, T., 2015. Desain Filter Digital Menggunakan Teknik Windowing dengan
Simulasi Berbasis Matlab. Jurnal Fakultas Teknik Universitas HKBP
Nommensen-Medan, Volume 3.
Tyson,
T.,
2013.
Introduction
to
Digital
Filter.
[Online]
Available
at:
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=15&ca
d=rja&uact=8&ved=2ahUKEwjPxZqRxaboAhWIaCsKHZE5BmIQFjAOegQI
BRAB&url=http%3A%2F%2F123.physics.ucdavis.edu%2Fweek_5_files%2Ffi
lters%2Fdigital_filter.pdf&usg=AOvVaw2LWC-HPL-iN3nBZzHd2IEz
[Accessed 19 March 2020].
20