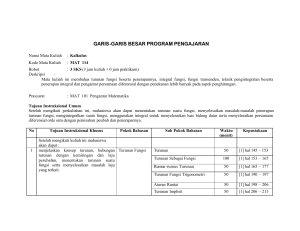
INTEGRAL LIPAT TIGA ATAU LEBIH
Makna integral lipat tiga :
∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧
.....(1) adalah :
𝑉
Pengintegralan pertama dilakukan terhadap x dengan menganggap y dan z konstan,
Pengintegralan kedua terhadap y dari hasil pengintegralan yang pertama, dengan
menganggap z konstan, dan yang terakhir
Hasil pengintegralan kedua di integralkan terhadap z
Pada integral lipat tiga, sebagai daerah integrasi V bukan lagi region dalam bidang xy tetapi
berupa luasan tertutup / permukaan dalam ruang.
1. Apabila batas-batas integrasi dinyatakan oleh
𝑥1 (𝑦, 𝑧) ≤ 𝑥 ≤ 𝑥2 (𝑦, 𝑧),
𝑦1 (𝑧) ≤ 𝑦 ≤ 𝑦2 (𝑧),
Maka integral (1) dapat ditulis :
𝑦2 (𝑧)
𝑧2
∫ ∫
𝑧1
𝑧1 ≤ 𝑧 ≤ 𝑧2
𝑥2 (𝑦,𝑧)
∫
𝑦1 (𝑧)
𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧
𝑥1 (𝑦,𝑧)
2. Apabila integral ∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑧𝑑𝑦𝑑𝑥
...... (2), batas integrasinya :
𝑉
𝑥1 ≤ 𝑥 ≤ 𝑥2 ,
𝑦1 (𝑥) ≤ 𝑦 ≤ 𝑦2 (𝑥), 𝑧1 (𝑥, 𝑦) ≤ 𝑧 ≤ 𝑧2 (𝑥, 𝑦)
Maka (2) selengkapnya ditulis :
𝑦2 (𝑥)
𝑥2
∫ ∫
𝑥1
𝑧2 (𝑥,𝑦)
∫
𝑦1 (𝑥)
𝑓(𝑥, 𝑦, 𝑧)𝑑𝑧𝑑𝑦𝑑𝑥
𝑧1 (𝑥,𝑦)
Dari intergral lipat tiga ini kita bisa mengembangkan intergral ganda yang lain seperti
lipat empat dan lipat lima dan seterusnya dengan aturan integrasi sebagaimana lipat
tiga.
Contoh – contoh :
C-1 : hitunglah
bila 𝑓(𝑥, 𝑦, 𝑧) = 2𝑥 + 𝑦 − 𝑧 dan
∭ 𝑓(𝑥, 𝑦, 𝑧)𝑑𝑧𝑑𝑦𝑑𝑥
𝑉
V adalah daerah tertutup yang dibatasi oleh : 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 𝑥 2 , 0 ≤ 𝑧 ≤ 𝑥 − 𝑦
Jawab : integralnya
1
𝑥2
𝑥−𝑦
∫ ∫ ∫
0
0
0
𝑥2
𝑥−𝑦
1
(2𝑥 + 𝑦 − 𝑧) 𝑑𝑧𝑑𝑦𝑑𝑥 = ∫ ∫ [2𝑥𝑦 + 𝑦𝑧 − 𝑧 2 ]
𝑑𝑦𝑑𝑥
2
0
0 0
1
𝑥2
1
1
= ∫0 ∫0 {(2𝑥(𝑥 − 𝑦) + 𝑦(𝑥 − 𝑦) − (𝑥 − 𝑦)2 ) − (0)} 𝑑𝑦𝑑𝑥
2
𝑥2
1
3
1
3
1
= 2 ∫0 ∫0 (𝑥 2 − 𝑦 2 ) 𝑑𝑦𝑑𝑥 = 2 ∫0 [𝑥 2 𝑦 − 3 𝑦 3 ]
1
3
1
3 1
1
1
𝑦 2 +𝑧 2
𝑧
1
𝑦 2 +𝑧 2
𝑧
Jawab: ∫0 ∫0 ∫0
1
1
8
0
35
1
1 1
𝑥𝑧𝑑𝑥𝑑𝑦𝑑𝑧
1
𝑦 2 +𝑧 2
𝑧
𝑥𝑧𝑑𝑥𝑑𝑦𝑑𝑧 = ∫0 ∫0 [12𝑥 2 𝑧]
0
𝑧
0
1
= 2 ∫0 (𝑥 4 − 3 𝑥 6 ) 𝑑𝑥 = 2 [5 𝑥 5 − 21 𝑥 7 ] =
C-2 : hitunglah ∫0 ∫0 ∫0
𝑥2
1
1
𝑑𝑦𝑑𝑧
𝑧
= 2 ∫0 ∫0 (𝑦 2 + 𝑧 2 )2 𝑧𝑑𝑦𝑑𝑧 = 2 ∫0 ∫0 (𝑦 4 𝑧 + 2𝑦 2 𝑧 3 + 𝑧 5 ) 𝑑𝑦𝑑𝑧
2
𝑧
= 2 ∫0 [ 5 𝑦 5 𝑧 + 3 𝑦 3 𝑧 3 + 𝑦𝑧 5 ] 𝑑𝑧 =
0
2
ln 𝑦
C-3 : hitung ∫0 ∫0
2
ln 𝑦
Jawab : ∫0 ∫0
2
−𝑦−𝑧
∫0
ln 𝑦
= ∫0 ∫0
−𝑦−𝑧
∫0
1 28 6
𝑧 𝑑𝑧
∫
2 0 15
1
=
2
15
𝑒 𝑥+𝑦+𝑧 𝑑𝑥𝑑𝑧𝑑𝑦
2
ln 𝑦
𝑒 𝑥+𝑦+𝑧 𝑑𝑥𝑑𝑧𝑑𝑦 = ∫0 ∫0
[𝑒 𝑥+𝑦+𝑧 ]−𝑦−𝑧
𝑑𝑧𝑑𝑦
0
2
𝑦
(𝑒 0 − 𝑒 𝑦+𝑧 ) 𝑑𝑧𝑑𝑦 = ∫0 [𝑧 − 𝑒 𝑦+𝑧 ]ln
0 𝑑𝑦
2
= ∫0 (ln 𝑦 − 𝑦𝑒 𝑦 + 𝑒 𝑦 ) 𝑑𝑦 = [𝑦 ln 𝑦 − 𝑦 − 𝑦𝑒 𝑦 + 𝑒 𝑦 + 𝑒 𝑦 ]20
= 1 − e + 2ln 2