Penentuan Parameter dan Arus Asut Motor Induksi 3 Phasa

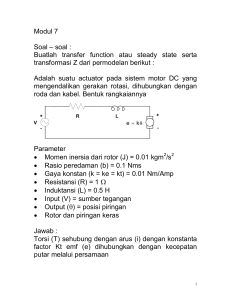
39
Penentuan Parameter dan Arus Asut
Motor Induksi Tiga Fasa
Yandri
Laboratorium Konversi Energi
Jurusan Teknik Elektro, Fakultas Teknik, Universitas Tanjungpura
e-mail : [email protected]
Abstrak– Tulisan ini membahas tentang penentuan
paramater motor induksi tiga fasa berdasarkan data
percobaan/pengujian yang mencakup percobaan tanpa
beban, percobaan rotor ditahan, dan percobaan DC.
Selain itu juga dilakukan perhitungan arus asut. Sampel
data yang diambil berupa 2 (dua) buah motor dengan
spesifikasi yang berbeda, yakni motor 7,5 hp dan motor
25 hp. Proses perhitungannya dilakukan dengan
menggunakan program MATLAB. Untuk motor 7,5 hp
memiliki parameter
= 0,2429 Ω ,
= 0,6706 Ω ,
= 0,1511 Ω ,
= 0,6706 Ω ,
= 14,0281 Ω ,
dan
= 87,9063 . Sedangkan untuk motor 25 hp
memiliki parameter
= 0,1055 Ω ,
= 0,2112 Ω ,
= 0,0708 Ω ,
= 0,3167 Ω ,
= 5,2474 Ω , dan
= 223,3343 . Untuk motor 7,5 hp dapat diasut
secara langsung, namun lebih baik jika digunakan
pengasut bintang-segitiga. Sedangkan untuk motor
25 hp dapat menggunakan pengasut ototransformator.
Kata kunci– parameter motor, arus asut, motor induksi
1. Pendahuluan
Pada hakekatnya tiap motor induksi memiliki
karakteristik torka-kecepatan yang berbeda-beda.
Dengan diketahuinya karakteristik suatu motor maka
pemilihan motor untuk penggerak beban dapat
dilakukan secara tepat. Namun, karakteristik tersebut
hanya dapat diketahui jika parameter motor yang
bersangkutan juga diketahui. Parameter tersebut
mencakup tahanan stator, reaktansi bocor stator, tahanan
rotor, reaktansi bocor rotor, reaktansi magnetisasi, dan
tahanan inti besi. Nilai parameter tersebut tidak akan
ditemukan pada pelat nama (name plate) sebuah motor.
Untuk mengetahuinya perlu dilakukan pengujian pada
motor tersebut yang mencakup percobaan tanpa beban,
percobaan rotor ditahan, dan percobaan DC.
Biasanya sebuah motor dapat menarik arus sekitar
5 hingga 7 kali dari arus nominal selama pengasutan.
Apabila torka beban selama pengasutan dan inersia
beban motor tidak besar, proses pengasutan hanya
membutuhkan waktu yang singkat, dengan demikian
temperatur motor tidak melebihi batas yang diijinkan.
Dalam aplikasi tersebut motor dapat diasut langsung ke
jala-jala dan ini biasanya diperuntukkan untuk motormotor berukuran kecil dan tidak demikian halnya untuk
motor-motor besar. Apabila torka beban selama
pengasutan tinggi atau inersia bebannya yang tinggi,
maka proses pengasutan akan membutuhkan waktu yang
cukup lama. Jika motor menarik arus yang besar selama
pengasutan, maka akan mengakibatkan kerusakan pada
motor akibat pemanasan lebih. Arus asut yang tinggi
juga dapat mengakibatkan terjadinya drop tegangan
yang besar pada jaringan. Dengan demikian metode
pengasutan secara tepat perlu diterapkan untuk motor
berkapasitas besar guna mengurangi arus asut dan drop
tegangan.
Untuk motor induksi rotor belitan, pengasutan dapat
dilakukan pada arus yang rendah dengan cara
menyisipkan tahanan luar pada rangkaian rotor selama
pengasutan. Tahanan luar ini tidak hanya memperbesar
torka asut tetapi juga dapat mengurangi arus asut.
Untuk motor induksi rotor sangkar, arus asut dapat
bervariasi dengan rentang yang lebar, tergantung pada
daya nominal motor dan tahanan rotor pada kondisi
pengasutan. Sedangkan metode pengasutan yang dapat
dilakukan dapat berupa pengasut bintang-segitiga /
Y − Δ (star-delta starter), pengasut ototransformator
(autotransformer starter), pengasut tahanan primer
(primary resistor starter), pengasut reaktor (reactor
starter), pengasut lilitan terpisah (part winding starter),
atau pengasut solid state (solid state starter).
2. Rangkaian Ekivalen Motor Induksi
Gbr.1(a) memperlihatkan rangkaian ekivalen per
fasa dari motor induksi, sedangkan gbr.1(b) merupakan
rangkaian ekivalen alternatif.
(a)
(b)
Gambar 1. Rangkaian ekivalen motor induksi
Jurnal ELKHA Vol.3, No.2, Juli 2011
40
Keterangan gbr :
R1  tahanan stator
X 1  reaktansi bocor stator
R2  tahanan rotor mengacu ke stator
X 2  reaktansi bocor rotor mengacu ke stator
Rc  tahanan inti besi
X M  reaktansi magnetisasi
I1  arus stator
I 2  arus rotor mengacu ke stator
V  tegangan sumber
E1  tegangan induksi stator
3. Penentuan Parameter Motor Induksi
Percobaan Tanpa Beban
Percobaan/pengujian tanpa beban (no-load test)
ditujukan untuk mengukur besarnya rugi-rugi putaran
motor serta memberikan informasi tentang arus
magnetisasi.
Rangkaian
untuk
percobaan
ini
diperlihatkan pada gbr. 2(a).
ekivalen motor ini diperlihatkan pada gbr 2(b). Dengan
nilai slip yang sangat kecil, nilai (1 − )/ jauh lebih
besar dibandingkan
serta jauh lebih besar
dibandingkan
. Pada kasus ini, rangkaian ekivalen
secara pendekatan dapat diubah menjadi rangkaian akhir
seperti terlihat pada gbr 2(b). Pada gambar, terlihat
bahwa tahanan output terhubung paralel dengan
reaktansi magnetisasi
dan rugi-rugi inti .
Pada kondisi tanpa beban ini, daya masuk diukur
dengan alat-alat ukur yang nilainya harusnya sama
dengan rugi-rugi pada motor. Rugi-rugi tembaga rotor
dapat diabaikan karena arus
bernilai sangat kecil
sekali [hal ini dikarenakan tahanan beban (1 − )/
yang sangat besar]. Rugi-rugi tembaga stator dalam hal
ini adalah :
(1)
=
sehingga daya masuk adalah :
=
+
+ & +
(2)
= 3
+
dimana
merupakan rugi-rugi putaran dari motor :
(3)
=
+ & +
Jadi, dengan memberikan daya masuk ke motor maka
rugi-rugi putaran mesin dapat ditentukan.
Rangkaian ekivalen yang melukiskan operasi motor
pada kondisi ini mengandung tahanan
dan
(1 − )/ yang terhubung paralel dengan reaktansi
magnetisasi
. Arus yang dibutuhkan untuk
menghasilkan medan magnet bernilai sangat besar pada
motor induksi, hal ini dikarenakan tingginya nilai
reluktansi dari celah udara, sehingga reaktansi
akan
bernilai jauh lebih kecil dibandingkan dengan nilai
tahanan yang paralel dengannya. Dengan arus lagging
yang besar, sebagian besar jatuh tegangan (voltage drop)
akan terjadi pada komponen-komponen induktif
rangkaian. Dengan demikian impedansi input ekivalen
secara pendekatan adalah :
(4)
=
≈
+
,
dan jika dengan cara lain
dapat ditentukan, maka
reaktansi magnetisasi
juga akan dapat diketahui.
Percobaan DC Untuk Penentuan Tahanan Stator
Gambar 2. Percobaan tanpa beban motor induksi :
(a) Rangkaian percobaan
(b) Rangkaian ekivalen yang diperoleh
Pada percobaan ini, dua wattmeter, satu voltmeter, dan
tiga amperemeter terhubung ke motor induksi. Selama
catu daya dihubungkan maka motor akan berputar. Pada
kondisi ini yang hanya merupakan beban motor adalah
rugi-rugi gesek dan angin ( & ), sehingga seluruh daya
listrik yang dikonversikan (
) diserap sebagai rugirugi mekanik, dan slip motor bernilai sangat kecil
(kemungkinan sekitar 0,001 atau kurang). Rangkaian
Tahanan rotor
memainkan peranan yang sangat
kritis pada operasi motor induksi. Diantaranya adalah,
menentukan
bentuk
kurva
torka-kecepatan,
menentukan juga kecepatan dimana terjadinya torka
maksimum. Percobaan motor standar yang dinamakan
dengan percobaan rotor ditahan dapat digunakan untuk
menentukan tahanan total motor (percobaan ini akan
dijelaskan pada sub bab berikutnya). Walaupun
demikian, percobaan ini hanya ditujukan untuk
menentukan besarnya tahanan total. Untuk menentukan
secara akurat, perlu kiranya untuk mengetahui
besarnya
sehingga
dapat diperoleh dengan cara
mengurangkan tahanan total dengan tahanan .
Ada suatu percobaan untuk menentukan
yang
nilainya tidak tergantung dari , , dan . Percobaan
Jurnal ELKHA Vol.3, No.2, Juli 2011
41
ini dinamakan dengan Pengujian / Percobaan DC
(DC Test). Ini dilakukan dengan menghubungkan belitan
stator motor induksi dengan tegangan DC. Karena
arusnya adalah arus DC, maka tidak ada tegangan yang
diinduksikan pada rangkaian rotor, dengan demikian
tidak ada arus yang mengalir pada rotor. Disamping itu,
pada arus DC, reaktansi motor bernilai nol. Dengan
demikian, satu-satunya arus yang membatasi motor
adalah tahanan stator dan karena itu besarnya tahanan
dapat ditentukan.
Rangkaian dasar untuk percobaan DC ini
diperlihatkan pada gbr. 3.
Gambar 3. Rangkaian percobaan untuk pengujian tahanan DC
Gambar ini memperlihatkan catu daya DC yang
dihubungkan pada dua dari tiga terminal motor induksi
yang terhubung Y. Untuk melakukan pengujian ini,
arus pada belitan stator diatur pada nilai nominal, dan
tegangan antar terminal diukur. Arus pada belitan stator
diatur ke nilai nominal sebagai upaya untuk
memanaskan belitan pada suhu yang sama dimana
belitan beroperasi selama kondisi normalnya (ingat,
tahanan belitan merupakan fungsi dari suhu).
Arus pada gbr. 3 mengalir melalui dua belitan,
sehingga tahanan total pada lintasan arus adalah 2 .
Oleh karena itu,
atau,
2
diperlihatkan pada gbr. 4(b). Perhatikan bahwa,
dikarenakan rotor tidak bergerak, slip
= 1, dan
dengan demikian / justru sama dengan
(nilainya
sangat kecil). Karena kecilnya nilai
dan
maka
hampir seluruh arus input akan mengalir melaluinya,
dibandingkan dengan arus yang mengalir melalui
yang nilainya jauh lebih besar. Oleh karena itu,
rangkaian pada kondisi ini terlihat seperti kombinasi seri
dari ,
,
, dan
.
Bagaimanapun juga terdapat suatu masalah dengan
percobaan ini. Pada operasi normalnya, frekuensi stator
merupakan frekuensi jala-jala dari sistem tenaga
(50 atau 60 Hz). Pada kondisi asut, frekuensi rotor juga
sama dengan frekuensi jala-jala. Akan tetapi, pada
kondisi operasi normalnya, slip sebagian besar motor
hanya bernilai 2 - 4 %, dan frekuensi rotor yang
dihasilkan berada pada rentang 1 - 3 Hz. Ini akan
menimbulkan suatu masalah karena frekuensi jala-jala
tidak merepresentasikan kondisi operasi normal dari
rotor. Untuk mengatasi hal ini biasanya diambil nilai
kompromi, yakni dengan menggunakan frekuensi
sebesar 25 % atau kurang dari frekuensi nominalnya.
=
(5)
2
Dengan nilai
ini maka rugi-rugi tembaga stator
pada kondisi tanpa beban dapat ditentukan, dan rugi-rugi
putaran dapat diperoleh dengan cara mengurangkan
daya masuk ( ) pada kondisi tanpa beban dengan
rugi-rugi tembaga stator (
).
=
Percobaan Rotor Ditahan
Percobaan ketiga yang dapat dilakukan pada motor
induksi guna menentukan parameter rangkaiannya
dinamakan dengan percobaan rotor ditahan (blockedrotor test / locked-rotor test). Pada percobaan ini, rotor
ditahan sehingga tidak dapat berputar, tegangan sumber
dihubungkan ke motor, selanjutnya ukur tegangan, arus,
dan daya yang dihasilkan.
Gambar 4 menunjukkan pengawatan untuk
percobaan rotor ditahan. Untuk melakukan percobaan
rotor ditahan ini, tegangan AC dihubungkan ke stator,
dan arus yang mengalir diatur mendekati nilai beban
penuh. Apabila arus pada kondisi nilai beban penuh,
selanjutnya ukur tegangan, arus, dan daya yang mengalir
ke motor. Rangkaian ekivalen untuk percobaan ini
Gambar 4. Percobaan rotor ditahan untuk motor induksi :
(a) Rangkaian percobaan, (b) Rangkaian ekivalen motor
Setelah catu daya dihubungkan ke motor, secepatnya
atur besarnya arus yang mengalir ke motor kira-kira
pada nilai nominalnya, kemudian ukur daya masuk,
tegangan, dan arus sebelum rotor mengalami banyak
pemanasan. Daya masuk ke motor diberikan melalui
persamaan berikut :
= √3
cos
jadi faktor daya rotor ditahan dapat diperoleh melalui
persamaan berikut :
(6)
√3
Besarnya impedansi total pada rangkaian motor pada
kondisi ini adalah :
PF = cos
|
|=
=
=
√3
(7)
Jurnal ELKHA Vol.3, No.2, Juli 2011
42
dan sudut impedansi totalnya adalah . Dengan
demikian,
=
+
(8)
= | | cos + | | sin
Tahanan rotor ditahan
sama dengan :
(9)
=
+
sedangkan reaktansi rotor ditahan
sama dengan :
(10)
=
+
dimana
dan
berturut-turut adalah reaktansi
stator dan rotor pada frekuensi pengujian / percobaan.
Tahanan rotor
sekarang dapat diperoleh melalui
persamaan berikut :
(11)
=
−
dimana 1 ditentukan melalui percobaan DC. Reaktansi
total rotor yang mengacu ke stator juga dapat diperoleh.
Karena reaktansi berbanding lurus dengan frekuensi
maka reaktansi total ekivalen pada frekuensi operasi
normalnya dapat diperoleh sebagai berikut :
=
=
(12)
+
Sayangnya, tidak ada cara yang sederhana untuk
memisahkan kontribusi reaktansi stator dan rotor satu
dengan lainnya. Selama bertahun-tahun, pengalaman
telah menunjukkan bahwa motor-motor dengan tipe
desain tertentu memiliki perbandingan tertentu antara
reaktansi stator dan rotornya. Hasil pengalaman tersebut
dirangkum pada tabel 1.
Tabel 1. Cara/metode berdasarkan pengalaman dan praktek
(rule of thumb) untuk menentukan besarnya
reaktansi stator dan rotor
dan
sebagai fungsi dari
Desain Rotor
0,5
0,5
0,4
0,3
0,5
Rotor belitan
Desain A
Desain B
Desain C
Desain D
0,5
0,5
0,6
0,7
0,5
Slip ( ) pada kondisi pengasutan adalah satu.
Dengan demikian berdasarkan gbr. 1(b) besarnya arus
asut dapat ditentukan dengan menggunakan persamaan
berikut :
dimana,
√3
(13)
)
+
(14)
)
+ ( +
menyatakan tegangan antar fasa, sedangkan
adalah tegangan fasa-netral.
=
+
+
(
=
Metode yang digunakan dalam penelitian ini berupa
pengumpulan data dua spesifikasi motor induksi dan
disertai dengan data hasil percobaan tanpa beban,
percobaan rotor ditahan, dan percobaan DC. Selanjutnya
dengan menggunakan program MATLAB dihitung
besarnya parameter dan arus asut motor induksi. Adapun
data motornya adalah sebagai berikut :
a) Motor induksi 3 fasa, 7,5 hp, 208 V, 60 Hz, 4 kutub,
desain A, hubungan Y dengan data hasil percobaan :
Tanpa beban = 208 V ; 8,17 A ; 420 W ; 60 Hz
Rotor ditahan = 25 V ; 27,9 A ; 920 W ; 15 Hz
Percobaan DC = 13,6 V ; 28 A
b) Motor induksi 3 fasa, 25 hp, 208 V, 60 Hz, 6 kutub,
desain B, hubungan Y dengan data hasil percobaan :
Tanpa beban = 208 V ; 22 A ; 1200 W ; 60 Hz
Rotor ditahan = 24,6 V ; 64,5 A ; 2200 W ; 15 Hz
Percobaan DC = 13,5 V ; 64 A
6. Hasil dan Pembahasan
Berikut adalah M-file untuk simulasi motor induksi tiga
fasa.
% =============================================
%
SIMULASI MOTOR INDUKSI TIGA FASA
% =============================================
%
Penentuan Parameter Motor berdasarkan
%
Data Percobaan (Percobaan Tanpa Beban,
%
Rotor Ditahan, dan Percobaan DC) serta
%
Perhitungan Arus Asut utk 2 Buah Motor
% =============================================
V_nl=[208 208] % tegangan tanpa beban (volt)
I_nl=[8.17 22] % arus tanpa beban (ampere)
P_nl=[420 1200]% daya tanpa beban (watt)
f_nl=[60 60]
% frekuensi tanpa beban (hertz)
V_lr=[25 24.6] % tegangan rotor ditahan (volt)
I_lr=[27.9 64.5] % arus rotor ditahan (ampere)
P_lr=[920 2200] % daya rotor ditahan (watt)
f_lr=[15 15] % frekuensi rotor ditahan (hertz)
Vdc=[13.6 13.5] % tegangan percobaan DC (volt)
Idc=[28 64]
% arus percobaan DC (ampere)
R1=Vdc./(2*Idc)
Vph_nl=V_nl/sqrt(3)
Z_nl=Vph_nl./I_nl
Vph_lr=V_lr/sqrt(3)
Z_lr=Vph_lr./I_lr
4. Persamaan Arus Asut Motor Induksi
=
5. Metode Penelitian
% tahanan stator (ohm)
cos_lr=P_lr./(sqrt(3).*V_lr.*I_lr)
theta_lr=acos(cos_lr)
degree_theta_lr=theta_lr*180/pi
R_lr=Z_lr.*cos(theta_lr)
R2=R_lr-R1 % tahanan rotor mengacu ke stator
(ohm)
X_lr_aks=Z_lr.*sin(theta_lr) % reaktansi rotor
ditahan pada frekuensi 15 Hz (ohm)
X_lr=X_lr_aks.*(f_nl/f_lr)
% reaktansi rotor
ditahan pada frekuensi 60 Hz (ohm)
X1=[0.5*X_lr(1) 0.4*X_lr(2)] % reaktansi bocor
stator (ohm)
X2=[0.5*X_lr(1) 0.6*X_lr(2)] % reaktansi bocor
rotor mengacu ke stator (ohm)
Xm=Z_nl-X1
% reaktansi magnetisasi (ohm)
Jurnal ELKHA Vol.3, No.2, Juli 2011
43
Vll=V_nl
Vph=Vll/sqrt(3)
Zf=j*Xm.*(R2+j.*X2)./(R2+j.*(X2+Xm))
Zin_start=R1+j*X1+Zf
I_start=Vph./Zin_start
mag_I_start=abs(I_start)
% arus asut (ampere)
disp('---------------------------------------------------------------------------')
disp('
Besaran
Motor A
Motor B')
disp('---------------------------------------------------------------------------')
disp(['Tahanan stator (ohm)
'num2str(R1(1,1)) '
'num2str(R1(1,2))])
disp(['Reaktansi bocor stator (ohm)
'num2str(X1(1,1)) '
'num2str(X1(1,2))])
disp(['Tahanan rotor mengacu ke stator (ohm)
'num2str(R2(1,1))'
'num2str(R2(1,2))])
disp(['Reaktansi bocor rotor mengacu ke stator
(ohm) 'num2str(X2(1,1)) '
'num2str(X2(1,2))])
disp(['Reaktansi magnetisasi (ohm)
'num2str(Xm(1,1)) '
'num2str(Xm(1,2))])
disp(['Arus asut (A)
'num2str(mag_I_start(1,1)) '
'num2str(mag_I_start(1,2))])
disp('---------------------------------------------------------------------------')
Gambar 6. Rangkaian ekivalen motor B (25 hp)
Dengan adanya rangkaian ekivalen tersebut di atas
maka karakteristik/kurva torka-kecepatan dan arus asut
untuk tiap-tiap motor dapat diketahui.
Berdasarkan tabel 2 dapat dilihat bahwa arus asut
motor B lebih besar dibandingkan motor A. Jika dikaji
dari pers. 13, besarnya arus asut tergantung pada
tegangan sumber dan impedansi input (impedansi total).
Arus asut berbanding lurus dengan tegangan sumber dan
berbanding terbalik dengan impedansi. Untuk tegangan
sumber yang besarnya sama, maka besar kecilnya arus
asut semata-mata hanya dipengaruhi oleh besarnya
impedansi. Dikarenakan impedansi total motor B lebih
kecil daripada motor A, dengan demikian arus asut
motor B akan lebih besar daripada motor A.
7. Kesimpulan
Eksekusi dari M-file tersebut di atas akan menghasilkan
besaran-besaran motor dalam bentuk parameter motor
induksi dan arus asut yang ditunjukkan pada Tabel 2.
Tabel 2. Parameter dan arus asut motor induksi tiga fasa
untuk 2 (dua) buah motor
------------------------------------------------------------------------------------Besaran
Motor A
Motor B
------------------------------------------------------------------------------------Tahanan stator (ohm)
0.2429
0.1055
Reaktansi bocor stator (ohm)
0.6706
0.2112
Tahanan rotor mengacu ke stator (ohm)
0.1511
0.0708
Reaktansi bocor rotor –
0.6706
0.3167
mengacu ke stator (ohm)
Reaktansi magnetisasi (ohm)
14.0281
5.2474
Arus asut (A)
87.9063
223.3343
-------------------------------------------------------------------------------------
Dari parameter yang diperoleh berdasarkan hasil
percobaan (percobaan tanpa beban, percobaan rotor
ditahan, dan percobaan DC), dengan demikian dapat
digambarkan rangkaian ekivalen untuk masing-masing
motor seperti tampak pada gbr. 5 dan gbr. 6.
Penentuan parameter motor perlu dilakukan agar
dapat diketahui karakteristik torka-kecepatan dan
besarnya arus asut.
Untuk motor induksi 7,5 hp memiliki parameter
= 0,2429 Ω ,
= 0,6706 Ω ,
= 0,1511 Ω ,
= 0,6706 Ω
,
= 14,0281 Ω
,
dan
= 87,9063 . Sedangkan untuk motor 25 hp
memiliki parameter
= 0,1055 Ω ,
= 0,2112 Ω ,
= 0,0708 Ω ,
= 0,3167 Ω ,
= 5,2474 Ω , dan
= 223,3343 .
Motor berkapasitas besar akan memiliki arus asut
yang lebih besar dibandingkan motor berkapasitas kecil.
Sistem pengasutan untuk motor 7,5 hp dapat berupa
pengasutan langsung, namun lebih baik jika digunakan
pengasut bintang-segitiga. Sedangkan untuk motor 25 hp
dapat menggunakan pengasut ototransformator.
Nilai tahanan stator ( ) yang diperoleh dari hasil
percobaan DC tidaklah begitu akurat karena
mengabaikan efek kulit yang terjadi apabila tegangan
AC dihubungkan ke belitan. Namun pendekatan dengan
metode ini sudah dianggap cukup memadai. Metode
dengan hasil akurat yang mengikutsertakan koreksi
terhadap temperatur dan efek kulit dapat merujuk pada
IEEE Standard 112.
Gambar 5. Rangkaian ekivalen motor A (7,5 hp)
Jurnal ELKHA Vol.3, No.2, Juli 2011
44
Referensi
Biografi
[1] Biran, A., M. Breiner. MATLAB 6 for Engineers. Prentice
Hall, Great Britain, 2002.
Yandri
lahir
di
Singkawang
pada
tanggal
29 Maret 1969. Gelar S1 diperoleh dari Universitas
Tanjungpura (UNTAN), Pontianak, pada tahun 1994.
Sedangkan Gelar S2 diperoleh dari Institut Teknologi
Bandung (ITB) pada tahun 2005. Sejak tahun 1999
hingga sekarang menjadi staf pengajar pada Jurusan
Teknik Elektro, Fakultas Teknik, UNTAN, Pontianak.
Bidang riset yang diminati mencakup Mesin-Mesin
Listrik dan Pembangkit Listrik Non Konvensional.
[2] Chomat, M. Electric Machines and Drives. InTech
Publisher, Croatia, 2011.
[3] Hanselman, D., B. Littlefield, Alih Bahasa: Jozep Edyanto.
MATLAB-Bahasa Komputasi Teknis. Penerbit ANDI,
Yogyakarta, 2000.
[4] Nagrath, I.J., D.P. Kothari. Electric Machines. McGrawHill, New Delhi, 1999.
[5] Petruzella, F.D, Alih Bahasa : Sumanto. Elektronik
Industri. Penerbit ANDI, Yogyakarta, 2001.
[6] Seung-Ki Sul. Control of Electric Machine Drive Systems.
John Wiley and Sons, Inc., New Jersey, 2011.
[7] Wildi, T. Electrical Machines, Drives, and Power Systems,
Sixth Edition, Prentice Hall, New Jersey, 2006.
Jurnal ELKHA Vol.3, No.2, Juli 2011
45
Jurnal ELKHA Vol.3, No.2, Juli 2011