Teori Pita Energi Untuk Zat Padat

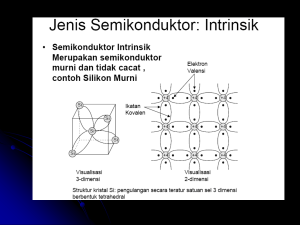
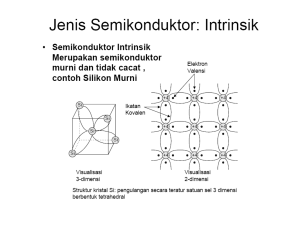
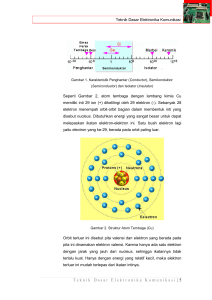
Bab 6
Elektron Dalam Zat Padat
(Teori Pita Energi)
Teori Pita Energi Untuk Zat Padat (Model Untuk Teori Pita Energi)
Berdasarkan daya hantar listrik, zat padat dibedakan menjadi tiga jenis :
•Logam dan semi-logam, dengan σ ≥ 105 ohm-1m-1.
•Semikonduktor, dengan 10-5 ohm-1m-1 ≤ σ ≥ 105 ohm-1m-1.
•Isolator, dengan σ ≥ 10-5 ohm-1m-1.
Tahanan Listrik (‘resisivity’ : ohm-m) dipengaruhi oleh SUHU. Pada bahan
LOGAM DAN SEMI-LOGAM resistivity akan MENINGKAT, tetapi pada bahan
SEMIKONDUKTOR resitivity ini akan MENURUN seiring dengan kenaikan suhu.
Untuk dapat menerangkan sifat daya hantar listrik zat padat diperlukan
sebuah model. Model yang dikembangkan adalah MODEL ELEKTRON BEBAS
TERKUANTISASI dan MODEL PITA ENERGI.
MODEL ELEKTRON BEBAS TERKUANTISASI tidak bisa menjelaskan rentang
nilai konduktivitas listrik zat padat yang lebar. Pada model ini potensial dari
gugus ion diabaikan (V=0).
MODEL PITA ENERGI dapat menjelaskan rentang nilai konduktivitas listrik zat
padat yang lebar. Pada model ini potensial dari gugus ion tidak diabaikan atau
adanya potensial berkala pada zat padat.
Lanjutan…..
Beberapa hal yang diperhatikan pada model PITA ENERGI:
•Adanya energi potensial periodik dalam keristal dengan keberkalaan kisi
kristal.
•Fungsi gelombangnya untuk kisi sempurna (tanpa vibrasi termal, cacar
geometri ataupun kimiawi).
•Merupakan teori elektron tunggal; hanya menelaah perilaku satu elektron saja
yang manan elektron ini dipengaruhi oleh potensial periodik yang
mempresentasikan semua interaksinya.
• Dapat menggunakan persamaan Schroendinger untuk mengkaji informasi
yang ada pada elektron tersebut dengan tetap mengikuti aturan sebaran
Fermi-Dirac untuk pengisian keadaan elektron.
•Teorema yang dapat digunakan untuk menguraikan bentuk dan sifat fungsi
Schroedinger untuk satu elektron dalam potensial berkala adalah Teorema
Bloch. Fungsi-fungsinya dikenal dengan Funsi Bloch.
Teori Pita Energi Untuk Zat Padat (Teorema Bloch, Bentuk dan Sifat Fungsi )
Dalam Telaah Bloch potensial periodiknya merupakan superposisi dua potensial:
1. Potensial berkala dari kisi-kisi gugus-gugus atom atau ion.
2. Potensial yang berasal dari semua elektron terluar atom-atom kristal.
Fungsi gelombang Schroedinger ketika ada potensial periodik untuk keberkalaan
kisi adalah:
Merupakan fungsi yang memiliki keberkalaan kisi kristal
Gambaran potensial periodik untuk kisi linier monoatomik
Persamaan Schroedinger untuk elektron dalam kristal
linier monoatomik dengan
Kesimpulan dari persamaan Schroendinger di atas adalah;
1. Jika
punya solusi untuk harga energi E, maka
Jika tedapat degenerasi maka
2. Dari syarat batas siklis Born-von Karmann didapat
ruang kristal yang terbatas.
juga punya solusi E.
untuk elektron
Teori Pita Energi Untuk Zat Padat (Teorema Bloch, Bentuk dan Sifat Fungsi )
Kesimpulan dari persamaan Schroendinger di atas adalah;
2. Untuk setiap X akan didapat yang berulang setelah N buah sel satuan.
Panjang kristal l=Na. Sehingga didapat;
3. Fungsi gelombang elektron bebas dalam satu dimensi adalah ;
untuk
potensial nol. Untuk potensial yang tidak nol fungsinya :
Dari fungsi
didapat
yang merupakan
fungsi periodik dengan keberkalaan a.
Potesial bernilai riil, artinya
sehingga didapat
Keduanya memiliki nilai eigen E, sehingga
.
Vektor k dan vektor kisi G memiliki dimensi yang sama. Semua harga k yang tepat
dapat dikembalikan ke selang harga k dalam daerah
. Selang ini
dinamakan Brillouin zone I.
Teorema Bloch memberikan bentuk dan sifat umum solusi persamaan Schroedinger
elektron dalam kisi periodik satu dimensi dan tidak memberikan solusi spesifik.
Teori Pita Energi Untuk Zat Padat (Model Kroning-Penney)
Model ini mengkaji perilaku elektron dalam kristal linier monoatomik dan
memberikan indikasi adanya selang energi elektron yang diperkenankan dan yang
tidak diperkenankan.
Model ini mempelajari perilaku elektron dalam potensial
dengan periode (a+b). Persamaan Schroedingernya;
. Solusi persamaan ini dibatasi harga E < Vo dan dibataskan pada
dua besaran riil, α dan β.
Dengan
mensubstitusikan solusi umum dari teorema Bloch ke
persamaan schroedinger akan didapatkan;
dengan solusi
dengan
A, B, C dan D ditetapkan berdasarkan syarat batas. Sehingga didapat empat
persamaan linier yang determinan solusinya tidak-sama dengan nol.
Penyemaan determinan sama dengan nol akan didapatkan;
Teori Pita Energi Untuk Zat Padat (Model Kroning-Penney)
Sketsa lengkung
adalah
, garis-garis
terputusnya adalah
, kedua nilai itu merupakan nilai maksimum dan
minimum cos ka, yang selanjutnya menjadi selang
dengan batasan
,
maka terbatasnya harga pada nilai tertentu juga membatasi energi yang dapat
dimiliki oleh elektron. Dengan demikian model ini memberikan informasi pita-pita
energi yang diperkenankan dan terlarang bagi elektron.
Kesimpulan umum dari lengkung
adalah;
1. Spektrum energi elektron terdiri dari beberapa pita energi.
2. Meningkatnya nilai akan memperlebar pita energi yang diperkenankan.
3. Bartambahnya P (bVo ), mempersempit lebar pita energi yang diperkenankan.
4. Jika P mendekati tak-hingga, artinya elektron berada dalam kotak potensial
berdinding tak-hingga dengan leber a.
5. Jika P mendekati nol, artinya elektron berada pada keadaan elektron bebas.
6. Diskontinue E terjadi pada
, yaitu pada
Teori Pita Energi Untuk Zat Padat (Model Kroning-Penney)
Di bawah ini adalah Sketsa ramalan harga energi elektron pada potensial periodik
kristal monoatomik linier dan kaitan model Kroning-Penney dengan harga energi
untuk elektron bebas dan elektron dalam kotak potensial berdinding tak-hingga.
Struktur level energi untuk derajat ikatan
yang berbeda
Teori Pita Energi Untuk Zat Padat (Model Kroning-Penney)
Kesimpulan umum dari persamaan
adalah;
1. Harga a tidak dapat ditentukan secara pasti, tetapi dapat diperkirakan
selanng nilai a yang diperbolehkan.
2. Diskontinuitas nilai a, terjadi pada coska bernilai +1 dan -1. yaitu saat
3. Selang terlarang harga (αa) terlarang tidak ada solusi pada
.
Sehinggga selang ini merupakan energi terlarang bagi elektron.
Model Elektron Hampir Bebas (Model Kisi Kosong)
Model elektron bebas mengasumsikan potensial kristal sangat lemah sehingga
elektron berprilaku hampir bebas.
Istilah kisi kosong di sini artinya meskipun potensila kristal dianggap sama dengan
nol, tetapi fungsi gelombang yang merupakan solusi persamaan Schroedinger
menaati sifat kesetangkupan kisi kristal. Persamaan untuk elektron ini adalah:
Spektrum kontinu,
seperti pada gambar
Gambar (a) menunjukkan extended zone
Gambar (b) menunjukkan reduced zone
Gambar (c) menunjukkan Brillouin zone I.
Di sini tidak ada pembatasan energi sehingga spektrum energinya kontinu.
Model kisi kosong ini membantu dalam memahami model elektron hampir bebas.
Model Elektron Hampir Bebas (Model Kisi Kosong)
Model elektron bebas mengasumsikan potensial kristal lemah tetapi tidak sama
dengan nol. Berdasarkan teorema Bloch untuk kristal satu dimensi, diskontinuitas
energi elektron pada batas-batas brillouin zone yaitu untuk
.
Daerah ini terdapat pada gambar;
Gambar (a) daerah reduced zone
Gambar (b) daerah extended zone
Loncatan antara dua daerah energi disebut energi gap. Untuk mengevaluasi
besarnya energi gap ini digunakan teori PETURBASI. Yang persamaannya adalah;
Hasil dari penjabaran teori peturbasi ini, memberikan bahwa energi gap pertama
dan kedua besarnya
dengan s
Model Elektron Hampir Bebas (Pemantulan Bragg)
Pada batas-batas Brillouin zone, fungsi Bloch berupa gelombang tegak dan bukan
gelombang berjalan, elektron dengan harga vektor propagasi ini memenuhi syarat
difraksi Bragg;
Karena pada hamburan elestik
, syarat Bragg menjadi
untuk kristal
monoatomik linier dengan jarak antar tetangga terdekatnya sebesar a syaratnya
menjadi
. Arti fisikanya adalah gelombang yang dipantulkan oleh atom
yang bersebelahan berbeda fasa π, atau 180 derajat. Superposisi dua gelombang
yang dipantulkan oleh atom yang bertetangganya adalah
, ini adalah
fungsi gelombang tegak dan bersifat genap. Selain itu juga dapat menghasilkan
kombinasi linier fungsi gelombang ganjil;
. Dari fungsi genap dan
ganjil ini akan didapatkan rapat muatan;
Rapat muatan genap yang berharga maksimum x=am.
Rapat muatan fungsi ganjil yang bernilai NOL di setiap kisi.
Logam, Isolator dan Semikonduktor (Pita energi dengan “Elektron states” yang
penuh dan kosong)
Sketsa hubungan E dan k model Kroning-Penney dalam pola zone
tereduksi. Lengkung E = E(k) memperlihatkan daerah energi
yang diperkenankan dan terlarang bagi elektron. Tetapi energi ini
masih bergantung pada jumlah elektron dalam kristal dan
statistika energi elektron.
Dua keadaan di mana medan listrik tidak menghasilkan arus netto dalam kristal:
1. Tidak ada elektron yang berada pada pita energi yang diperbolehkan.
2. Pita energi yang diperkenankan terisi penuh elektron.
Rapat arus elektron ini adalah;
Hanya pita energi yang terisi (atau kosong) sebagian yang dapat memberikan
sumbangan pada arus listrik.
Logam, Isolator dan Semikonduktor (Presentasi pembawa muatan)
Akibat medan listrik elektron di A akan bergerak ke arah –X dan
sampai pada kedudukan A’. Pada saat itu terjadi pantulan Bragg,
dan elektron muncul kembali di A’’. Kemudian elektron
menempuh siklus yang sama. Proses berulang ini disebut sebagai
osilasi Zener.
Rapat arus yang disumbangkan oleh pita energi yang tidak seluruhnya penuh,
diberikan oleh persamaan;
Untuk pembawa muatan elektron
Untuk pembawa muatan hole.
Model pita energi ini yang membedakan isolator, konduktor dan semikonduktor
Logam, Isolator dan Semikonduktor (Presentasi pembawa muatan)
Model pita energi ini yang membedakan isolator, konduktor dan semikonduktor
berdasarkan diagram pita energi yang dimilikinya.
Diagram pita energi untuk bahan
isolator, konduktor dan semikonduktir.
Latihan soal
1.
Apa yang dimaksud dengan energi Fermi?
Energi Fermi EF merupakan energi maksimum yang dapat dimiliki elektron
dalam kristal pada suhu T=0.
2.
Bagaimana keadaan energi Fermi pada bahan isolator, konduktor dan
semikonduktor berdasarkan teori pita energi?
Pada bahan Isolator tingkat energi Ferminya melintas daerah energi terlarang.
Pada bahan Konduktor tingkat energi Ferminya melalui pita konduksi,
sehingga pada suhu T=0 kelvin, semua ‘electron states’ dalam pita konduksi
dengan E< EF terisi.
Pada bahan Semikonduktor tingkat energinya melalui pita velensi, daerah
energi terlarang. Pada suhu T=0 kelvin, pita konduksi di bawah terisi semua
‘electron states’-nya, sedangkan dalam pita konduksi di atasnya semua ‘electron
states’ lowong.
Latihan soal
3.
Kondisi seperti apakah, dalam kristal tidak menghasilkan arus netto meskipun
ada medan listrik yang bekerja padanya?
Pada saat semua ‘electron states’ dalam pita energi yang diperkenankan sama
sekali tidak dihuni elektron atau pada saat semua ‘electron states’ dalam pita
energi yang diperkenankan terisi elektron, artinya tidak satupun ‘electron
states’ yang kosong.
4.
Kenapa model elektron bebas tidak dapat menjelaskan rentang harga
konduktivitas listrik zat padat yang lebar?
Karena pada model elektron bebas mengabaikan potensial dari gugus-gugus
ion dalam kristal (V=0).
5.
Kenapa model Teori pita dapat menjelaskan rentang harga konduktivitas listrik
zat padat yang lebar?
Pada model ini potensial dari gugus-gugus ion dalam kristal tidak sama dengan
nol, tetapi potensial ini merupakan potensial periodik yang berkaitan dengan
kisi kristalnya.
Latihan soal
6.
Jelaskan kenapa pada teori pita energi berlaku potensialnyaV(x+a) = V(x)?
Karena pada teori pita potensial dari gugus-gugus ion dalam kristalnya
dianggap merupakan potensial periodik. Potensial periodik ini dikenalkan
karena pada kisi kristalnya dianggap berulang secara periodik juga. Dengan
demikian ion-ion identiknya terpisah sejauh jarak a dari tetangga terdekatnya
sesuai dengan kisi kritalnya. Sebagimana digambarkan pada gambar di bawah
ini.