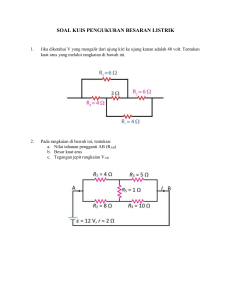
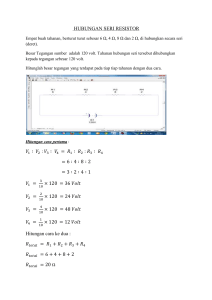
1. TUGAS PENDAHULUAN MATA KULIAH PENGUKURAN LISTRIK DASAR SEMESTER GENAP 2018/2019 Kode Mata Kuliah/SKS : EL 306223/3 Kelas 1B – D4 Teknik Listrik DEVI FITRIANA RAMLI 42118033 KELAS 1B – DIV Teknik Listrik Dosen pembimbing : - Sofyan, ST., MT (Pj) Sulhan Bone, S.ST., MT Ahmad Rosyid Idris, ST., MT Andriani Asri, ST., MT PROGRAM STUDI D-4 TEKNIK LISTRIK JURUSAN TEKNIK ELEKTRO POLITEKNIK NEGERI UJUNG PANDANG MAKASSAR 2019 2 Contoh penyelesaian soal dengan teorema Thevenin Perhatikan gambar rangkaian berikut ini: Tentukanlah berapa besar nilai arus yang mengalir melalui tahanan R2 (IR2)? Jawab: Langkah-langkahnya adalah: Tentukan titik terminal a-b dimana parameter ditanyakan. Pada rangkaian gambar 1.6 titik terminal a-b dapat ditentukan di tahanan R2. Maka komponen R2 dilepaskan dan diganti dengan titik a-b. Sumber tegangan bebasnya diganti dengan rangkaian short circuit. Kemudian mencari tahanan Theveninnya. 3 Rangkaian dibuat seperti Gambar 1.8. untuk memudahkan mencari tahanan Theveninnya. Dapat diperoleh: R1 . R3 RTh = R1 + R3 4Ω . 1Ω RTh = 4 Ω +1 Ω = 4Ω 5Ω = 0,8 Ω Pasang kembali sumber tegangannya, kemudian hitung nilai tegangan theveninnya. Kita umpamakan tegangan pada titik terminal a-b dengan V1 > V2, maka dapat diperoleh persamaan: ITh = V1 – V2 R 1 + R3 4 VTh = V1 – ITh . R1 atau VTh = V2 + ITh . R3 Maka , ITh = = 28 v – 7 v 4 Ω+ 1 Ω 21 v 5Ω = 4,2 VTh = 28 v – 4,2 A . 4 Ω atau VTh = 7 v + 4,2 A . 1 Ω = 28 v – 16,8 v = 11,2 v = 7 v + 4,2 v = 11,2 v Gambarkan kembali rangkaian pengganti Theveninnya (rangkaian aktif) dan pasang kembali komponen tahanan R2 yang tadi dilepas. Rangkaian Aktif Maka dapat diperoleh besar nilai arus yang mengalir pada tahanan R2 (IR2), yaitu: VTh IR2 = RTh + R2 IR3 = 11,2 v 0,8 Ω +2 Ω = 11,2 v 2,8 Ω =4 Contoh penyelesaian soal dengan teorema Norton Perhatikan gambar rangkaian berikut ini: 5 Tentukanlah berapa besar nilai arus yang mengalir melalui tahanan R2 (IR2)? Jawab: Langkah-langkahnya adalah: 1. Tentukan titik terminal a-b dimana parameter ditanyakan. Pada rangkaian gambar 1.6 titik terminal a-b dapat ditentukan di tahanan R2. Maka komponen R2 dilepaskan dan diganti dengan titik a-b. 2. Sumber tegangan bebasnya diganti dengan rangkaian short circuit. Kemudian mencari tahanan Nortonnya. 6 Rangkaian dibuat seperti Gambar 2.9. untuk memudahkan mencari tahanan Nortonnya. Dapat diperoleh: RN = RN = R1 . R3 R1 + R3 4Ω . 1Ω 4 Ω +1 Ω = 4Ω 5Ω = 0,8 Ω 3. Pasang kembali sumber tegangannya. 4. Kemudian titik a-b dihubungkan singkat. Sehingga IN dapat diperoleh dengan: IN = I1 + I2 Sehingga diperoleh 7 IN = = V1 R1 V2 + 28 V 4Ω R3 + 7V 1Ω =7A+7A = 14 A 8 Carilah nilai I dengan menggunakan teori Δ ke Y Penyelesaian: Bila kita melihat resistor R1, R2, dan R3 sebagai suatu rangkaian Δ (pada rumus berturut-turut Rab, Rac, dan R bc) dan ingin menggantinya dengan rangkaian Y,kita bisa mengubah rangkaian jembatan ini menjadi rangkaian yang lebih sederhana yaitu rangkaian seri-paralel: RA R1. R2 R1 R2 R3 RB R1.R3 R1 R 2 R3 9 12.18 12 18 6 12.6 12 18 6 216 6 36 72 2 36 RC R 2.R3 R1 R 2 R3 18.6 12 18 6 108 3 36 Sekarang kita telah mendapatkan rangkaian yang lebih sederhana. Kita bisa menganalisarangkaian ini menggunakan aturan seri-paralel: Serikan rangkaian R B dan R4 serta rangkaian Rc dan R5 RS1 = RB + R4 = 2Ω + 3Ω = 5 Ω 10 RS2= RC + R5 = 3 Ω + 12Ω = 15 Ω sehingga terbentuk rangkaian seperti ini: selanjutnya, hambatan RS1 dan RS2 dipararelkan RS 1 // RS 2 RP Rp RSI .RS 2 RS 1 RS 2 5.15 75 3 5 15 25 Dan terbentuk rangkaian seri seperti ini : 11 Dan rangkaian diatas dihitung secara seri menjadi RT RT = RA+ RP =6+3=9Ω Lalu hitung I dengan menggunakan hukum Ohm I V RT 10 1,11Ampere 9 Rangkaian pada gambar dibawah ini, hitung RT, dan I dengan menggunakan metode Y ke Δ Konversikan “Y” menjadi “Δ” ekivalensinya, karena resistor yang tersambung “Y”memiliki nilai-nilai yang sama. Ekivalen “Δ” nya akan memiliki nilai-nilai resistor sebesar RΔ = 3 (10 Ω) =30 Ω Sehingga rangkaiannya menjadi gambar di bawah ini. 12 Selanjutnya, kita paralelkan 30Ω // 30Ω, 60Ω // 30Ω serta 30Ω // 90Ω RP1 30..30 900 15 30 30 60 RP 2 60..60 1800 20 60 30 90 Sehingga rangkaiannya menjadi gambar di bawah ini. Kita lihat bahwa sisi yang dihasilkan “Δ” adalah susunan paralel, sehingga nilai totalresistansinya dapat dihitung dengan mudah RT RP1 //( RP 2 RP 3 RT 15..(20 22,5) 15 (20 22,5) RT 15..42,5 15 42,5 13 RT 637 11,08 5,75 Sehingga nilai arusnya adalah I V 30 I 2,7 Ampere RT 11,08 14 DAFTAR PUSTAKA Cut Zarmayra Zahra, F. (n.d.). academia. Retrieved maret 19, 2019, from academia web site: https://www.academia.edu/6467346/Rangkaian_Listrik_I__Teorema_Thevenin_dan_Norton https://www.academia.edu/6844184/Resume_7_Rangkaian_Listrik_1_Transformasi_ Delta_Wye_