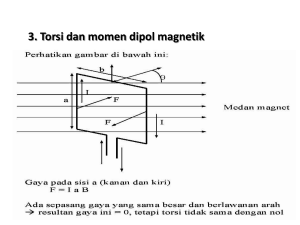
Modul 5. Fisika Dasar II I. MEDAN MAGNET Tujuan Instruksional Khusus Mahasiswa diharapkan dapat memahami pentingnya penggunaan Hukum Ampere dalam menghitung besarnya induksi magnet. II. Materi MEDAN MAGNET 2.1 Hukum Ampere 2.2 Torsi pada Loop Arus 2.3 Efek Hall 2.4 Bahan magnet III.Pembahasan 2.1 Hukum Amper Pada penjelasan mengenai induksi magnet oleh kawat lurus berarus menyatakan , bahwa : - vektor B di sekitar kawat lurus berarus arahnya mengelilingi kawat tersebut - Besarnya vektor B di sepanjang lingkaran dengan jari-jari tertentu yang berpusat pada kawat berharga konstan Untuk menentukan induksi magnet dapat menggunakan hukum Ampere. Jika kita memiliki suatu lengkungan tertutu C yang mengelilingi suatu kawat berarus i. hokum ampere menyatakan bahwa dalam ruang vakum integral garis adalah diperoleh persamaan sebagai berikut : atau , maka ( 6.1 ) Menurut Hukum Ampere untuk menentukan B di dalam solenoida adalah sebagai berikut : dapat dianggap hanya terdapat di dalam solenoida dan searah dengan sumbu solenoida (Gambar 6.1 ) .Disini i adalah arus yang terkandung di dalam lengkunga abcda . maka , dapat ditulis sebagai berikut : tegak lurus dan karena pada cd induksi magnet nol. Sehingga diperoleh sejajar karena pada ab, yatu sudut antaranya adalah θ sama dengan nol. Dimana atau . adalah panjang garis ab . Arus i yang terkandung dalam lengkungan abcda dapat ditentukan berikutnya. Bila sepanjang seluruh solenoida terdapat N buah lilitan yang sama rapatnya, dan tiap lilitan dialiri arus i. Sehingga arus dalam tiap satuan panjang solenoida adalah NI/ L. Karena lengkungan ab memiliki panjang , maka arus i yang terkandung didalamnya ialah : , maka Jika n = N/L , diperoleh persamaan untuk Solenoida adalah sebagai berikut : ( 6.2 ) B a d b c Gambar 6.1 Medan magnet B di dalam Solenoida Untuk menentukan besarnya medan magnet B di dalam suatu Toroida (Gambar 6.2 ) sebagai berikut : atau (6.3 ) P Gambar 6.2 Toroida berarus I , Arah medan di dalam kumparan berhimpit dengan garis singgung di setiap titik. I masuk I keluar Contoh 1 : Solenoida tipis dengan panjang 10 cm memiliki jumlah lilitan sebanyak 400 lilitan kawat dan membawa arus 2 Ampere. Hitung medan di dalam di dekat pusat . Penyelesaian : Jumlah lilitan persatuan panjang Contoh 2 : Sebuah kumparan datar yang terdiri dari 40 lilitan berdiameter 32 cm. Berapakah arus yang harus melaluinya agar pada titik pusat kumparan timbul medan dengan besar rapat fluksnya 3x10-4 W/m2 ? Penelesaian : atau jadi 2.2 Torsi pada Loop Arus; Momen Magnet Suatu arus listrik mengalir pada loop kawat tertutup yang diletakkan dalam medan magnet ( Gambar 6.3 ). Pada loop berarus tersbut bekerja momen gaya atau torsi magnet untuk memutar loop. i F1 b F2 i B a Gambar 6.3 Loop berarus dalam medan magnet Gaya pada sisi yang segaris dengan medan magnet B bernilai nol, sedangkan sisi yang tegak lurus dengan B besarnya sama. F1 = F2 = i b B dengan arah yang berlawanan dan terpisah pada jarak a. Momen tersebut dapat dinyatakan sebagai berikut : ( 6.4 ) A = luas loop Jika A dan B membentuk Sudut q ( Gambar 6.4 ), maka momen kopel yang bekerja pada loop berarus adalah : ( 6.5 ) disebut momen ( dipole) magnetik atau dilambangkan dengan m Vektor ,dapat dinyatakan dengan persamaan sebagai beikut : ( 6.6 ) Dari persamaan ( 5.5) dan ( 5.6 ) , diperoleh persamaan : ( 6.7 ) F1 m B F2 Gambar 6.4 Kawat segiempat berarus bersudut q terhadap B 2.3 Efek Hall Ketika konduktor pembawa arus tertahan pada medan magnet, medan memberikan gaya menyamping pada muatan-muatan yang mengalir pada konduktor. Pada gambar 6.5 elektron-elektron bergerak ke kanan konduktor persegi panjang , sehingga medan magnet akan memberikan gaya ke bawah pada elektron-elektron . Beda potensial pada permukaan R dan S akan bertambah tinggi dan medan listrik EH memberikan gaya e EH pada muatan-muatan yang sama dan berlawanan dengan gaya magnet. Efek ini disebut efek Hall. x R x x x x + + + + + + + + + + FH S - - - - - - - - - - x x x x x Gambar 6.5 Efek Hall dimana muatan negatip bergerak ke kanan dan muatan positip bergerak ke kiri R - - - - - - - - - Å FH S + + + + + + + + Pada kesetimbangan, gaya yang disebabkan oleh medan listrik diimbangi oleh gaya magnet , sehingga persamaan diperoleh sebagai berikut atau : ( 6.8 ) 2.4 Bahan Magnet Sifat magnetik bahan sebagian besar berasal dari gerak orbital elektron dan besaran yang disebut spin. Telah dibahas sebelumnya bahwa arus yang membentuk loop menghasilkan momen magnet m . Akibat adanya gerak orbital electron , maka atom-atom memiliki momen dipol magnet permanen. Besara-besaran inilah yang menentukan sifat dari magnetik bahan. Pada prinsip Pauli, menyatakan bahwa pada hal tertentu atom-atom bahan secara keseluruhan tidak memiliki momen dipole magnetik permanent yang disebut bahan diamagnetik. Bahan Diamagnetik dibedakan menjadi dua bagian, yaitu : bahan Paramagnetik dan bahan Feromagnetik. Momen dipol bahan Paramagnetik berarah acak, sehingga jumlah momen dipol magnet dalam seluruh bahan berharga nol. Sedangkan untuk bahan Feromagnetik , jika sebelumnya pernah mengalami medan magnet luar maka jumlah momen magnetnya tidak nol. Kuat lemahnya reaksi suatu bahan terhadap medan magnet luar yang mengenainya dinyatakan dengan besaran yang disebut suseptibilitas ( kepekaan ) magnetik yang dinyatakan dengan symbol c m . Jumlah momen magnet per satuan volume disebut sebagai magnetisasi M. Besaran medan magnet dinyatakan dengan H, maka : (6.9 ) Sifat-sifat magnetik dinyatakan sebagai berikut : -1 < c c m 0 < c c m > > < m 0 : bahan diamagnetik = 0 : bahan non magnetik ( ruang hampa ) m < 1 1 : bahan paramagnetik : bahan feromagnetik Hubungan antara induksi magnetik B dan intensitas magnet H dinyatakan oleh persamaan : ( 6.10 ) Dari persamaan ( 5.9 ) dan ( 5.10 ) diperoleh : atau (6 11 ) m adalah permeabilitas magnetik . Contoh 3 : Pita tembaga panjang yang lebarnya 1,8 cm dan tebal 1 mm diletakkan pada medan magnet 1,2 Tesla. Jika arus tetap 15 Ampere melewatinya, ggl Hall diukur sebesar 1,02 m Volt. Tentukan kecepatan alir electron dan kecepatan electron ( penghantar ) bebas ( jumlah satuan per volume ) pada tembaga. Penelesaian : Contoh 4 : Suatu Toroida dengan 300 lilitan/m dialiri arus listrik sebesar 5 Ampere. Jika ruang di dalam kumparan toroida diisi dengan besi yang mempunyai permeabilitas magnetic sebesar 5000 . Hitunglah B , H dan M di dalam besi tersebut . Penyelesaian: Tugas-tugas 1.Kawat lurus sepanjang 15 cm berarus 6 A berada dalam medan homogen yang diinduksi magnetiknya 0,4 Tesla. Berapa gaya yang diderita kawat , jika kawat : a. tegak lurus medan b. membentuk sudut 30 o dengan medan 2. Solenoida ( dalam udara ) sepanjang 50 cm terdiri atas 4000 lilitan. Dengan arus 0,25 A yang mengalir, Hitunglah B didalam solenoida tersebut . 3. Sebuah kumparan datar dengan lilitan berdiameter 10 cm terdiri dari 25 lilitan . Dengan arus 4 A dalam kawatnya. Berapa induksi magnetik B yang ditimbulkan pada titik pusat kumparan ? 4. Toroida ( dalam udara ) dengan jari-jari 5 cm terdiri dari 750 lilitan . Berapaarus yang mengalir dalam lilitan agar rapat fluks pada titik lingkaran Toroida sebesar 1,8x10- 3 Tesla ? Daftar Pustaka 1. Giancoli,' Fisika 2 ‘ , Penerbit Erlangga,edisi ke lima, Jakarta,2001 2. Drs.Soeharto,' Fisika Dasar II ‘ , Pt Gramedia Pustaka Utama, Jakarta, 1995 3. Frederick J.Bueche,'Fisika', Edisi ke delapan, Erlangga,1997