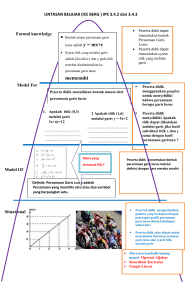
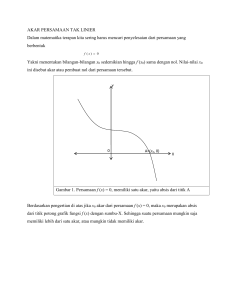
Matematika Ekonomi Pertemuan 1 Ekasatya Aldila Afriansyah Persamaan Linier Matematika Ekonomi 1. Koordinat Cartesius 2. Kemiringan dan Persamaan Garis 3. Titik-titik potong persamaan garis 2 Koordinat Kartesius Matematika Ekonomi 3 Koordinat Kartesius Matematika Ekonomi 4 Latihan Matematika Ekonomi • Tunjukkan titik P, Q, R, dan S yang koordinatnya berturut-turut (4,1), (1,4), (-5,2), dan (-4,2) dalam satu bidang koordinat. 5 Matematika Ekonomi Kemiringan dan Persamaan Garis • Garis Lurus Garis yang ditarik melalui dua titik yaitu (x ,y ) dan (x ,y ) 1 2 1 2 • Kemiringan Garis Garis yang melalui titik A (x ,y ) dan B (x ,y ) dengan x ≠ x maka kemiringan (gradien) dilambangkan dengan notasi m. 𝑃𝑒𝑟𝑢𝑏𝑎ℎ𝑎𝑛 𝑡𝑒𝑔𝑎𝑘 𝑦2 − 𝑦1 𝑚= = 𝑃𝑒𝑟𝑢𝑏𝑎ℎ𝑎𝑛 𝑚𝑒𝑛𝑑𝑎𝑡𝑎𝑟 𝑥2 − 𝑥1 1 1 1 2 2 2 6 Matematika Ekonomi Kemiringan dan Persamaan Garis • Persamaan Garis Persamaan yang melalui titik (0,0) dengan kemiringan m 𝑦 = 𝑚𝑥 Persamaan yang melalui titik (x ,y ) dengan kemiringan m 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1 ) 1 1 Persamaan yang melalui dua titik yaitu (x ,y ) dan (x ,y ), dengan kemiringan m 𝑦 − 𝑦1 𝑥 − 𝑥1 = 𝑦2 − 𝑦1 𝑥2 − 𝑥1 1 1 2 2 7 Matematika Ekonomi Kemiringan dan Persamaan Garis • Persamaan Garis Tegak Persamaan garis tegak adalah x = k, dengan k suatu konstanta • Persamaan Garis Datar Persamaan garis datar adalah y = k, dengan k suatu konstanta Latihan Gambarkan persamaan garis: 𝑥 = 3 𝑑𝑎𝑛 𝑦 = 0 8 Matematika Ekonomi Kemiringan dan Persamaan Garis • Persamaan Linier Bentuk umum persamaan linier adalah 𝐴𝑥 + 𝐵𝑦 = 𝐶 Dengan A dan B tidak nol, pangkat x dan y adalah satu, dan nilai C dalam penerapan ekonomi dan bisnis sering disebut sebagai kendala (constraint) dari sumber daya. Latihan Cari persamaan garis yang melalui titik A (-4, 2) dan B (6,-1) Cari persamaan garis yang melalui titik P (3,2) dan Q (8,4) 9 Matematika Ekonomi Kemiringan dan Persamaan Garis • Grafik Persamaan Grafik suatu persamaan dalam x dan y terdiri atas titik-titik di bidang yang koordinat-koordinatnya memenuhi suatu persamaan. Prosedur menggambar grafik Langkah 1: Dapatkan koordinat-koordinat beberapa titik yang memenuhi persamaan Langkah 2: Hubungkan titik-titik tersebut dengan sebuah kurva mulus Latihan Gambarlah grafik persamaan 𝑦 = 𝑥 2 − 4 dan 𝑦 = 2𝑥 − 3 dalam satu bidang koordinat yang sama. 10 Matematika Ekonomi Titik-titik potong persamaan garis • Perpotongan dengan sumbu x. Koordinat titik potong suatu grafik dengan sumbu-x adalah (..., 0). Ini berarti untuk mencari titik potong sumbu-x dapat diperoleh dengan cara menetapkan nilai y = 0. • Perpotongan dengan sumbu y. Koordinat titik potong suatu grafik dengan sumbu-y adalah (0, ...). Ini berarti untuk mencari titik potong sumbu-y dapat diperoleh dengan cara menetapkan nilai x = 0. Latihan Cari titik potong sumbu-x dan sumbu-y dari 𝑦 2 − 𝑥 + 𝑦 − 6 = 0 11 Soal-soal 1. 2. Matematika Ekonomi 1 Tentukan titik potong garis 𝑦 = −2𝑞 + 2 dan 𝑦 = 𝑞 2 2 Carilah titik potong garis 𝑦 = −𝑥 + 1 dan 𝑦 = 2𝑥 − + 25 4𝑥 − 2 3. Cari nilai k agar garis 4𝑥 + 𝑘𝑦 = 5 melalui titik (2,1) 4. Laporan sebuah survey di India menyebutkan bahwa populasi penduduk suatu negara berhubungan linier dengan waktu. Sebagai contoh dikemukakan bahwa penduduk di negara bagian A pada tahun 1980 berjumlah 80 juta dan pada tahun 1990 populasinya menjadi 93 juta. Dari data tersebut, tuliskanlah persamaan linier yang mengaitkan jumlah penduduk (y) dengan waktu (t). Berapakah populasi penduduk Negara bagian A pada tahun 2000, 2004, dan 2014? 12 Soal-soal Matematika Ekonomi 5. Menurut data yang telah dikumpulkan sebelumnya, ekspektasi umur pria di tahun 1980 adalah 68 tahun. Kemudian pada tahun 1994 mengalami kenaikan menjadi 75 tahun. Buatlah model persamaan dari kasus tersebut dan tentukan ekspektasi umur pria pada tahun 2000 dan 2014. 6. Sebuah mobil bernilai 120 juta dan setiap tahun mengalami depresiasi sebesar 8% dari nilai awalnya. Cari sebuah model persamaan untuk y, yaitu harga mobil setelah t tahun. 13 Soal-soal Matematika Ekonomi 7. Sebuah mesin fotocopy seharga 80 juta telah dibeli hari ini. Mesin tersebut akan mengalami depresiasi secara linier sampai nilainya itu seharga 2 juta setelah 20 tahun. Tuliskan model persamaan untuk y, yaitu harga mesin fotocopy tersebut setelah t tahun. 8. Biaya C untuk menghasilkan x unit barang 3 ditunjukkan oleh persamaan linier 𝐶 = 𝑥 + 4 200 (juta). Kemiringan grafiknya dinamakan biaya marjinal. Carilah kemiringan itu dan berikan arti ekonominya. 14