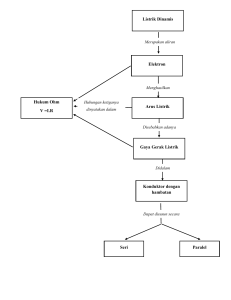
BAB SATU PENDAHULUAN 1.1 LATAR BELAKANG Sejarah peradaban manusia tidak dapat dipisahkan dengan perkembangan teknologi material pada zaman tersebut. Zaman batu merupakan zaman dimana batu dijadikan material utama perkakas sehari-hari. Zaman batu berubah menjadi zaman besi dengan ditemukan dan diaplikasikannya besi dalam masyarakat saat itu. Penemuan material baru yang dikuti dengan aplikasi akan memberikan perubahan dalam masyarakat. Kebenaran hal ini dapat diamati dari kemajuan pesat dari berbahai bidang seperti energi, telekomunikasi, multimedia, komputer, konstruksi dan transportasi. Kita tidak mungkin naik pesawat jet jarak jauh bila tidak ditemukan material baru untuk pembuatan mesin jet yang berbeda dengan mesin lainnya. Juga aplikasi komputer dalam segala bidang tak mungkin ada bila teknologi material untuk rangkaian mikroelektronik tidak mengalami kemajuan pesat seperti sekarang. Pada saat ini dimana dunia terasa semakin kecil, faktor jarak hampir tidak berpengaruh dalam komunikasi. Itupun tidak luput dari pesatnya perkembangan aplikasi material dalam telekomunikasi. Pendek kata penemuan dan aplikasi material baru dapat membuat dunia baru yang boleh jadi tidak pernah dibayangkan oleh si penemu sendiri. Penemu semi konduktor tidak pernah membayangkan sebelumnya bahwa dengan semikonduktor akan terjadi revolusi komunikasi. Dalam memasuki milenium ketiga perlu juga diantisipasi material baru apa yang akan diaplikasikan sehingga terjadi sesuatu yang baru di alam global. Profesi kerekayasaan sangat erat terkait dengan material. Acreditation Board for Engineering and Technology (ABET) memberikan penjelasan mengenai kerekayasaan sebagai berikut : “Engineering is the profession in which a knowledge of the mathematical and natural sciences gained by study, experience, and practice is applied with judgement to develop ways to utilize economically the materials and forces of nature for the benefit of mankind.” Pendahuluan Van Vlack dalam kasus yang serupa menyatakan bahwa “What do engineers do ? “. “Engineers adapt materials and energies for society ‘s needs “. Seorang insinyur mengadaptasi material dan energy untuk keperluan masyarakat. Profesi sebagai insinyur harus dibekali dengan pemahaman tentang material. Dalam menjalankan tugas kerekayasaan selalu dihadapkan dengan pemilihan material yang cocok dan tidak jarang harus melakukan modifikasi atau proses supaya memenuhi syarat syarat tekno-ekonomis. Seorang insinyur elektro harus berbekal diri dengan pemahaman tentang material material yang terkait dengan dunia elektroteknik. Berikut adalah sebuah model sain dan rekayasa material yang diajukan oleh Van Vlack. Gambar 1.1: model sain dan rekayasa material Basic science dan engineering sangat diperlukan untuk mengetahui struktur material. Dari pihak masyarakat sebagai pengguna memerlukan suatu untuk kerja (performance) tertentu dari material tersebut. Dari kedua arah ini dilakukan investigasi sifat (properties) material dan selanjutnya dilakukan processing untuk memenuhi kebutuhan masyarakat. Dalam siklus proses di atas maka baik pengalaman scientific maupun pengalaman empirik sangat diperlukan. 1.2. TEORI ELEKTRON KLASIK Yang mula-mula membahas secara teoritik mengenai elektron dalam zat padat adalah Druce dan dimodifikasi oleh Lorentz. Model mereka mengasumsikan bahwa semua elektron yang berada pada pita velensi dari material (khususnya logam) berperilaku sebagaimana molekul gas. Dengan demikian elektron memenuhi hukum kinetik gas dan sesuai dengan statistik Maxwell-Boltzmann. Potensial di dalam logam diasumsikan konstan dan lebih kecil dari permukaan. Elektron-elektron bergerak secara bebas di dalam logam dan dibatasi oleh dinding Material Elektroteknik potensial yang lebih tinggi pada permukaan logam. Kasus ini menjadi pembahasan yang sangat lazim dilakukan. pada teori kuantum yaitu kasus elektron yang terperangkap sumur potensial yang akan dibahas secara mendalam pada bab II. Sesuai dengan teori Druce-Lorentz maka energi rata-rata yang dimiliki oleh awan elektron di sekitar inti atom dalam suatu kisi kristal dinyatakan sebagai Ue = 3 /2.NkT (1-1) Dimana N jumlah elektron per unit volume, k konstanta Boltzmann dan T Temperatur. Bila N diambil bilangan Avogadro,Ue akan merupakan energi internal molar dari elektron. Meskipun teori yang disampaikan oleh Druce—Lorentz merupakan kemajuan dari sebelumnya namun masih belum bisa menjelaskan fenomena thermoelectric dimana setiap logam berperilaku berbeda-beda sedangkan menurut Druce-Lorentz semestinya sama. 1.3. LATAR BELAKANG TEORI ELEKTRON MODERN Teori elektron modern telah dimulai dari karya Planck (1901) ketika menjelaskan radiasi benda hitam. Semua zat padat dan cair ketika dipanaskan sekitar 700 derajat Celcius maka akan memancarkan radiasi dengan daya yang bervariasi sesuai dengan panjang gelombang. Peristiwa ini dijelaskan dengan terjadinya osilasi atom di dalam zat padat atau cair yang dipicu oleh pemanasan (thermal). Spektrum radiasi hampir sama untuk berbagai zat dan sering disebut dengan spektrum benda hitam. Suatu benda Pendahuluan hitam sempurna akan menyerap semua radiasi yang mengenainya. Dengan demikian bila ada benda hitam memancarkan radiasi maka radiasi tersebut adalah berasal dari dalam benda. Intensitas radiasi tergantung dari temperatur. Spektrum radiasi I𝜆 merupakan radiasi per satuan panjang gelombang. Sehingga I𝜆, d𝜆 merupakan intensitas ~dalam suatu range d𝜆. Teori klasik menyatakan bahwa pergerakan atom di permukaan material menghasilkan gelombang elektromagnetik. Gelombang elektromagnetik berinterferensi satu dengan yang lain menghasilkan gelombang berdiri dengan berbagai panjang gelombang. Setiap panjang gelombang terkait dengan. energi tertentu. Dalam teori klasik diprediksikan bahwa intensitas mempunyai hubungan I𝜆 ~ 1/𝜆4 dan I𝜆 ~ T seperti diusulkan oleh Rayleigh-Jean. Namum formula ini tidak dapat menjelaskan hasil eksperimen terutama untuk gelombang pendek seperti pada gambar. Planck menjelaskan dengan pendekatan yang baru. Permukaan radiasi disusun oleh dipol-dipol listrik yang berosilasi dan energi radiasi terkait dengan frekuensi osilasi dari dipol-dipol tersebut. Berbeda dengan pernyataan teori klasik bahwa energi dari osilator dapat berubah secara kontinu maka Planck mempostulatkan bahwa energi osilator tidaklah kontinu melainkan diskrit. Ini merupakan kontribusi besar Planck pada perkembangan teori kuantum. Planck mempostulatkan beberapa hal berikut dalam menjelaskan radiasi benda hitam: a. b. c. Energi osilator mempunyai bentuk E= nhf, dimana n adalah bilangan bulat, h konstanta Planck= 6,626 x 10-27 erg-s dan f adalah frekuensi osilator. Hal ini berarti bahwa energi osilator merupakan kelipatan diskrit dari suatu harga yang tergantung dari frekuensi. Karena energi suatu osilator adalah diskrit maka transisi dari satu level energi ke level lainnya juga diskrit yang akan memberikan absorbsi atau emisi radiasi Energi yang diperoleh atau dilepas selama transisi dari level satu ke level lainnya berharga diskrit berupa kuanta. 𝐼= 2𝜋ℎ𝑐 2 ℎ𝑐 𝜆5 [exp( )−1] 𝜆𝐾𝑡 (1-2) Suatu rumus diusulkan untuk menjelaskan hubungan antara spektrum daya radiasi dimana h adalah konstanta Planck, c kecepatan cahaya, k konstanta Boltzmann dan 𝜆 adalah panjang gelombang. Material Elektroteknik 1.4. EFEK FOTOLISTRIK Hertz (1887)`menunjukkan bahwa radiasi dapat mengeluarkan elektron dari permukaan logam. Ketika antara elektroda terdapat tegangan dan diberikan radiasi maka elektron yang keluar akan dipercepat dan mengalirlah arus listrik. Elektron untuk lepas dari logam perlu tambahan energi sebesar W yang disebut dengan fungsi kerja (work function) yang merupakan harga spesifik untuk tiap logam. Dalam teori klasik energi kinetik elektron yang terlepas tergantung dari intensitas radiasi sehingga makin tinggi intensitas radiasi makin tinggi energi kinetik elektron. Namun demikian pada kenyataan eksperimen menunjukkan bahwa energi kinetik elektron yang terlepas ditentukan oleh frekuensi radias i dan bukan intensitas radiasi. Ada frekuensi minimum radiasi sehingga efek fotolistrik terjadi yang berkaitan dengan energi minimum yang diperlukan oleh elektron untuk terlepas dari logam. Intensitas radiasi menentukan banyaknya elektron yang terlepas. Ketika katoda diradiasi dengan cahaya dan frekuensi lebih besar dari harga tertentu maka amperemeter menunjukkan arus I meskipun tegangan anoda nol (baterai dihubung singkat). Hal ini disebabkan elektron yang terlepas dari katoda mempunyai energi kinetik yang cukup besar untuk dapat mencapai elektroda lawan. Bila tegangan positif diberikan kepada anoda maka akan memperbanyak elektron yang mengalir dan berarti pula memperbesar arus yang ditunjukkan oleh Pendahuluan amperemeter. Di pihak lain bila bila tegangan negatif diberikan kepada anoda maka potensial akan berfungsi sebagai penghambat elektron karena gaya elektrostatik mendorong elektron untuk tidak mendekati anoda. Hasil eksperimen untuk suatu frekuensi radiasi ditunjukkan oleh gambar 1.4. Tegangan Vo adalah tegangan yang tepat menghentikan laju elektron yang terlepas. Untuk itu memenuhi hubungan eVo = ½ me v2 = KE (1-3) dimana KE adalah energi kinetik elektron. Peningkatan intensitas radiasi meningkatkan arus yang mengalir akan tetapi memerlukan tegangan bias yang sama untuk menghentikan arus. Hal ini menunjukkan bahwa energi kinetik elektron yang terlepas tidak tergantung oleh intensitas radiasi dan jumlah elektron yang terlepas ditentukan oleh intensitas radiasi. Di sinilah salah satu perbedaan dengan teori klasik dimana menyatakan bahwa energi kinetik elektron ditentukan oleh intensitas radiasi. Material Elektroteknik Gambar 1.5 menunjukkan hubungan antara arus dan tegangan lawan untuk suatu intensitas dan berbagai frekuensi radiasi. Untuk frekuensi yang berbeda diperlukan tegangan lawan yang berbeda pula. Hal ini menunjukkan bahwa energi kinetik elektron yang terlepas tergantung dari frekuensi radiasi. Gambar 1.6 menunjukkan hubungan antara frekuensi dengan energi kinetik elektron untuk berbagai metal. Pendahuluan Gambar 1.6 : energi kinetik sebagai fungsi dari frekuensi radiasi untuk berbagai metal Untuk berbagai metal yang berbeda didapatkan frekuensi ambang yang berbedabeda untuk elektron dapat terlepas. Juga didapatkan kemiringan yang sama seperti terlihat jelas dalam gambar. Dari beberapa hasil di atas Einstein menjelaskan efek fotolistrik sebagai berikut. 1. 2. 3. 4. Radiasi terdiri dari pulsa diskrit yang disebut dengan photon Photon dipancarkan atau diserap secara diskrit Setiap photon mempunyai energi diskrit sebagai kelipatan dari hv dimana v adalah frekuensi Photon berperilaku sebagai gelombang sesuai dengan frekuensi v Untuk terjadi emisi elektron diperlukan energi minimum sebesar Work function W. Energi kinetik elektron tergantung dari energi photon. KE = eV = hf -W (1-4) Dengan V sebagai fungsi dari f maka dari differensiasi didapat dV/df = h/e (1-5) Ini adalah suatu konstanta yang tidak tergantung dari bahan. Konstanta ini adalah kemiringan fungsi V - f. Perpotongan sumbu V terhadap garis V - f adalah tegangan yang berkorelasi dengan fungsi kerja yaitu Vo e = W (electron volts) Tabel 1.1 Fungsi kerja (work function) beberapa logam Material Fungsi Kerja (eV) Perak (Ag) 4,26 Alumunium (Al) 4,28 Emas (Au) 5,1 Cesium (Cs) 2,14 Tembaga (Cu) 4,65 Lithium (Li) 2,3 Magnesium (Mg) 3,7 Natrium (Na) 2,75 Material Elektroteknik 1.5. ELEKTRON SEBAGAI PARTIKEL DAN GELOMBANG Pada fotolistrik, cahaya yang dikenal sebagai gelombang ternyata berperilaku seperti sekelompok partikel dengan energi sesuai dengan frekuensi yang disebut dengan photon. Apakah elektron yang sering dianggap sebagai partikel berperilaku sebagai gelombang ? Percobaan interferensi dan diffraksi elektron menunjukkan bahwa elektron berperilaku juga sebagai gelombang. De Broglie menyatakan hubungan antara sifat sebagai partikel dan sebagai gelombang dengan persamaan λ =h/p (1-6) dimana 𝜆 adalah panjang gelombang yang mewakili sifat gelombang dari elektron sedangkan p adalah momentum yang merupakan suatu besaran yang terkait dengan sifat sebagai partikel. Dalam hal ini partikel dapat disimulasikan sebagai sekelompok gelombang atau paket gelombang. Paket gelombang berpropagasi dengan kecepatan group Vg. Gelombang individual di dalam paket bergerak dengan kecepatan yang lain. Momentum merupakan produk dari massa dan kecepatan maka 𝜆 = h/m.vp (1-7) Panjang gelombang dan frekuensi terkait dengan persamaan v = 𝜆f (1-8) Kombinasi dari persamaan persamaan ini didapat 𝜆= ℎ 𝑚𝑐 2 𝑐 2 . = 𝑚 𝑉𝑝 ℎ 𝑉𝑝 Dari persamaan ini terlihat bahwa kecepatan gelombang berbanding terbalik dengan kecepatan partikel. Pendahuluan Gelombang dalam paket dapat dinyatakan sebagai superposisi dari dua gelombang dengan sedikit perbedaan panjang gelombang. Pada daerah pusat amplitudo tinggi terjadi karena interferensi konstruktif dan pada daerah pinggiran amplitudo kecil karena interferensi destruktif. Kecepatan group dinyatakan sebagai v=𝜆f; f= v/𝜆 = vk (1-10) Hubungan antara panjang gelombang dan bilangan gelombang adalah sehingga k𝜆 = 1 (1-11) Dengan demikian didapatkan kecepatan group sebagai 𝑑𝑣 𝑘 Ve = v - 𝜆 𝑑𝑡 = 𝑣 − [ − 𝑑𝑘 ] [ 𝑑 𝑓−𝑣 𝑑𝑘 𝑘 𝑑𝑣 ] = 𝑑𝑘 (1-12) Dengan memanfaatkan hubungan energi pada teori klasik dan teori kuantum didapatkan hubungan E = ½ mv2 = h f (1-13) atau Selanjutnya dengan pangaturan posisi didapatkan 𝑑𝑣 𝑑𝜆 ℎ 𝑑𝑓 ℎ 𝑉𝑔 = 𝑚𝑣 . 𝑑𝜆 = − 𝑚𝑣 . 𝜆2 Perhitungan selanjutnya dapat diperoleh untuk v = vg (1-14) Material Elektroteknik dv m Dan dengan integrasi persamaan ini didapatkan v = h/m/1, atau (1-14) (1-15) = h/mv = h/p (1-16) Ini tidak lain adalah persamaan de Broglie 1.6 PRINSIP KETIDAKPASTIAN HEISENBERG Suatu fungsi gelombang dari elektron bebas terkait dengan suatu gelombang dengan panjang gelombang tertentu. Gelombang menjalar di seluruh posisi dengan probabilitas uniform. Dengan demikian ketidakpastian posisi Δx dari elektron tak hingga. Karena panjang gelombang sudah tertentu maka momentum juga tertentu, berarti ketidakpastian momentum Δp adalah nol karena kita mengetahui dengan pasti besarnya px, dari persamaan de Broglie, px = h / 𝜆 Untuk suatu elektron terperangkap pada sumur potensial dengan lebar a maka ketidakpastian posisi adalah a. Momentum adalah px = hk untuk arah x positif dan untuk arah x negatif ketidakpastian AP adalah Apx=2hk Untuk kondisi dasar (ground state) maka ka = Tc Apx = 2hz la Perkalian dua ketidakpastian didapat Ax.Ap = a. 2hz = h (1-17) (1-18) (1-19) Dari hasil ini ditemukan bahwa tidak mungkin posisi dan momentum elektron / partikel dapat ditentukan secara eksak pada saat bersamaan. Prinsip ini disebut dengan prinsip ketidakpastian Heisenberg dengan rumusan Ax.Ap h (1-20) Dengan cara yang sama didapat ketidakpastian energi dan waktu AE .At (1-21)