I. Pendahuluan

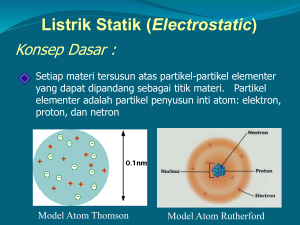
I. Pendahuluan
Listrik Magnet
Listrik Æ berkaitan dengan teknologi modern: komputer, motor
dsb.
Bukan hanya itu Æ
1
Muatan Listrik
Contoh klassik: Penggaris digosok-gosok pada kain kering
Æ tarik-menarik dengan kertas-kertas kecil
Dikenal ada dua jenis muatan:
Æ positif dan negatif
sejenis Æ tolak menolak
tidak sejenis Æ tarik menarik
Asal mula muatan?
Æ Æ atom
Inti diam
elektron mudah bergerak
benda bermuatan positif Æ ada atom yang kehilangan elektron
benda bermuatan negatif Æ ada kelebihan elektron
Mengapa muatan di udara cepat hilang?
Æ apa maksud “hilang”?
Æ benda menjadi netral
Karena muatan “bocor” ke (uap) air yang berada di udara.
O
-molekul polar
+
H
H +
Udara kering: sering ada muatan statik
Hujan: susah untuk menahan muatan
Jenis bahan:
2
(a) Konduktor, contoh: logam Æe- tidak terikat kuat oleh inti atom
(b) Isolator, contoh kayu Æ e- terikat kuat
(c) Semikonduktor, contoh Ge, Si
Mengukur Muatan:
Æ elektroskope / elektrometer
prinsip kerja:
+++ +
++
++
Hukum Coulomb
Q1
++
+++
Q2
++
r
Q1
F=k
Q2
Q1Q 2
r2
Kemana arah gaya?
3
F21
F12
Sejenis:
Q2
Q1
F21
F12
Tak sejenis:
Q2
Q1
Secara vektor:
F12 = k
Q 1Q 2
r21
r213
r21
y
Q1
F12
r1
F21
Q2
r2
x
[pada catatan ini cetak tebal Æ vektor]
Arti notasi:
F12 Æ gaya pada muatan Q1 karena muatan Q2
r1 Æ posisi muatan Q1
r2 Æ posisi muatan Q2
r21 Æ vektor posisi dari Q2 menuju Q1
Bila Q1 dan Q2 sejenis maka Q1Q2 > 0 gaya pada Q1 akan menjauhi
Q2 Æ gaya repulsif (totak menolak).
Sebaliknya bila Q1 dan Q2 tak sejenis maka Q1Q2 < 0 gaya pada Q1
akan mendekati Q2 Æ gaya atraktif (tarik menarik).
4
Catatan kesulitan siswa dalam memahami arah gaya:
Rancu antara tanda ± yang berarti “jenis gaya” dan arah gaya
sesungguhnya.
Bila Q1 dan Q2 sejenis maka Q1Q2 > 0
Æ gaya positif (repulsif)
Sebaliknya bila Q1 dan Q2 tak sejenis maka Q1Q2 < 0
Æ gaya negatif (attraktif)
Î namun untuk melihat arah gaya kita harus lihat pada muatan
yang mana gaya itu bekerja:
Untuk Q1 dan Q2 sejenis:
F21
F12
Q1
Q2
x
Nilai F Æ positif (repulsif)
Lihat pada Q1 Æ gaya mengarah ke sumbu x negatif
pada Q2 Æ gaya mengarah ke sumbu x positif
Saran:
Perhatikan gambar (diagram) secara visual untuk menentukan arah
gaya, bukan asal memasukkan angka-angka muatan.
[Berpikir!!! bukan menghapal rumus!]
Satuan-satuan:
5
F=k
Q1Q 2
r2
Muatan Q1, Q2 Æ Coulomb (C) atau μC
1 μ C = 10-6 C
Gaya, F Æ Newton (N)
Jarak, r Æ meter (m)
konstanta k Æ
k = 8,988x109 N m2/C2
Muatan elementer, muatan terkecil.
Æ muatan sebuah elektron
Æ (atau muatan sebuah proton)
e = 1,6021892 x 10-19 Coulomb
Æ tidak ada muatan yang lebih kecil lagi.
ee- e- eee- ee- e- eee-
Muatan suatu benda selalu kelipatan e.
Catatan kecil:
Ahli Fisika partikel elementer (juga ahli Fisika energi tinggi, 1963)
berteori bahwa ada partikel yang lebih kecil, disebut quark, yang
mempunyai muatan 2/3 e atau 1/3 e. Deteksi eksperimen secara
langsung pada partikel-partikel ini sulit dimungkinkan karena
secara teori tidak ada quark bebas.
6
Contoh-contoh soal
(1). Hitung besar gaya listrik pada sebuah elektron dalam atom
hidrogen (karena tertarik oleh sebuah proton, Q2 = e). Jarak
rata-rata proton-elektron: 0,53x10-10 m.
Jawab:
Q1 = - e = - 1,6 x 10-19 C
Q2 = e = 1,6 x 10-19 C
r = 0,53x10-10 m
F=k
Q1Q 2
r2
9
= 9,0x10
(-1,6 x 10-19 )(1,6 x 10-19 )
( 0,53x10− 10 ) 2
= −8,2x10− 8 N
tanda negatif berarti attraktif.
(Kemana arah gaya? Æ gaya pada elektron mengarah ke proton)
(2). Hitung gaya (net gaya) yang bekerja pada partikel 3 pada
gambar berikut karena dua muatan yang lain.
0,3 m
Q1 = - 3 μC
Q2 = + 5 μC
0,2 m
Q3 = - 4 μC
7
Jawab:
Gaya-gaya yang bekerja pada partikel 3:
F32
F31
=k
F31
Q 3 Q1
2
r13
9
= 9x10
( −4x10− 6 )( −3x10− 6 )
( 0,5)
2
= 1,2 N
(tolak menolak)
F32
9
= 9x10
( +5x10 − 6 )( −3x10 − 6 )
(0,2)
2
= −4,5 N
(tarik menarik)
F = F32 + F31 = -3,3 N
Latihan:
Q3 = 7 μ C
15 cm
30o
Q2 = 5 μ C
26 cm
Q1 = -2 μ C
Hitung gaya pada Q3!
8
Konstanta k sering dinyatakan dalam εo Æ permitivitas
k=
F=
1
4πε o
1 Q1Q 2
4πε o r 2
Nilai numerik εo = 8,85x10-12 C2/Nm2
Medan listrik
Ide dasar:
Sebuah muatan Æ menimbulkan “pengaruh”
Æ “medan” listrik
E = F/q
1 Q
E=
4 πε o r 2
Apabila muatan “sumber” terdiri dari beberapa buah:
9
E1
E4
Æ medan listrik total:
E = E1 + E2 + E3 + ……………..
= Σ Ei
(jumlah vektor)
Untuk muatan kontinu:
Sebagaimana biasanya:
dm
dE
E = ∫ dE
(perhatikan arah!!)
Contoh kasus:
Carilah medan listrik sebuah kawat panjang uniform pada suatu
jarak a dari kawat tersebut
10
r
y
θ
dEx = dE cos θ
a
dEy
dE =
dE
1 dQ
λ
dy
=
4πε o r 2 4πε o ( y 2 + a 2 )
Ey = 0 (lihat gambar, karena simetri)
λ ∞ cos θ dy
E = Ex = ∫ dE cos θ =
∫
4 πε o −∞ ( y 2 + a 2 )
karena
y = a tan θ
maka
dy = a sec2 θ d θ
batas integral berubah:
y = - ∞ Æ θ = - π/2
y = ∞ Æ θ = π/2
Sehingga:
11
π
E
2 cos θ a sec 2 θ
λ
dθ
=
∫
4 πε o π (a 2 tan 2 θ + a 2 )
−
=
E
=
2
π
1 2
λ
∫ cos θ dθ
4 πε o a π
−
λ 1
2 πε o a
karena tan2 θ + 1 = sec2 θ
2
(2) Medan yang plat (bidang) uniform bermuatan berbentuk bujur
sangkar LxL pada suatu jarak z di atas pusat bujur sangkar.
Ukuran z jauh lebih kecil dari L.
z << L
z
+
+
+
+
+
+
+
+
+
+
+
+
+ +
L
L
Penyelesaian:
Plat ini kita bagi-bagi menjadi berbagai elemen muatan yang
berbentuk garis lurus (kotak panjang) dengan panjang L dan lebar dy,
tinggi sama dengan tinggi plat.
12
dE
θ
dEz
dEy
z
r
dy
y
O
y
x
karena z << L
Æ elemen kotak panjang dapat dianggap sebagai elemen garis tak
berhingga
Lihat kembali hasil sebelumnya:
persamaan ini E =
λ 1
menjadi: (untuk elemen garis)
2 πε o a
dQ
L1
2πε o r
Apa arti dQ disini?
Æ elemen muatan yang berada pada elemen luas L dy
dE =
Jadi kalau kita definisikan σ = muatan per-satuan luas
Æ dQ = σ L dy
Sehingga:
13
dE =
σ dy
2 πε o r
z
dE
θ
dEz
dEy
z
r
dy
y
O
y
x
Karena simetri maka Ey = 0
Sehingga:
E = Ez = ∫ dE cos θ
Seterusnya:
dy
σ
cos θ
∫
2 πε o r
Æ ada tiga variabel y, r dan θ dalam integral Æ harus diubah
E=
cos θ = z / r Æ disini z bukan variabel!
14
sedangkan r = √ z2 + y2
Integral menjadi:
σ L/ 2
z
E=
dy
∫
/
3
2
2 πε o − L/ 2 2
z + y2
(
)
Æ silahkan teruskan evaluasi integral ini.
Akan didapat:
σ
y y = L/ 2
E=
atan
2 πε o
z y=− L/ 2
Untuk L yang sangat besar Æ ∞ (dibandingkan z)
σ
2ε o
Perhatikan untuk plat besar sejajar yang dipisahkan pada jarak d,
masing-masing mempunyai rapat muatan + σ dan - σ
+
E+
E- +
E+ E+
E+
+
E- +
E = E+ + E- = 0 +
E = E+ + E- = 0
+
+ E = E+ + E- σ
+
=
εo
Medan listik bernilai uniform diantara dua plat
E=
15
Garis Gaya
Æ “garis/kurva hayal” yang menunjukkan/menghubungkan arah
gaya apabila diberi “test charge” sebuah muatan positif.
Muatan tunggal:
Positif
Negatif
+
-
Pasangan Muatan:
Tak sejenis
+
Sejenis
-
+
+
16
Plat Paralel:
-
+
+
+
+
+
+
Contoh soal:
Sebuah elektron (e-) dipercepat dalam sebuah medan uniform E
dengan besar 2x104 N/C berasal dari dua plat paralel dengan jarak
1,5 cm. Elektron dipercepat dari plat negatif dan melewati sebuah
lubang kecil di plat positif. Hitung kecepatan elektron ketika keluar
dari lubang?
Jawab:
-
+
+
E
-
+
e
-
v
+
17
F=qE
ma=qE
qE (1,6x10− 19 )( 2x104 )
a=
=
= 3,5x1015 m / det 2
m
9,1x10− 31
Dari kinematika:
v = √ 2 a x = 1,0x107 m/det
Dipole Listrik
Kombinasi muatan positif +Q dan muatan negatif -Q pada jarak L.
Contoh molekul CO.
C == O
++ -Moment dipol (vektor) p = Q L mempunyai arah dari - Q ke + Q
+Q
p
-Q
18
Dipol dalam pengaruh medan listrik uniform
+Q
F
p
-Q
F
E
Pada muatan + Q Æ ada gaya F = QE
Pada muatan - Q Æ ada gaya F = - QE
Disini terlihat:
∑ F = 0 tetap torsi (τ) tidak sama dengan nol
τ=r×F
Besar τ:
Bila sudut mula-mula antara L dan E : θ
τ = ½ L sin θ QE + ½ L sin θ QE
= p E sin θ
jadi
τ=p×E
19
Kerja
W=
θ2
θ2
θ1
θ1
∫ τ dθ = pE ∫ sin θ dθ
W = pE (cos θ1 - cos θ2)
Usaha untuk mempertahankan posisi dipol:
U = - W = - pE cos θ
U=-p•E
Soal: Hitung medan yang ditimbulkan oleh dipole pada jarak r dari
titik tengah yang membagi dipol (jarak tegak lurus).
Jawab:
r
E=
1
p
4πε o ( r 2 + L2 / 4) 3 / 2
20
Hukum Gauss
Hukum ini menghubungkan muatan dan medan listrik.
Æ bentuk lebih umum dan elegant dari hukum Coulomb
Terlebih dahulu kita definisikan fluks listrik:
ΦE = E A (medan tegak lurus permukaan)
Untuk medan yang tidak tegak lurus permukaan:
θ
θ
Fluks
A (vektor normal
permukaan)
E
ΦE = E A⊥
= E A cos θ
21
Jadi
ΦE = E • A
Fisis? Æ jumlah garis gaya yang menembus bidang
Untuk Medan Listrik yang tidak Uniform:
Ei
ΔAi
ΦE =∑ Ei • ΔAi
Secara umum:
ΦE = ∫ Ei •dAi
Pada Permukaan Tertutup
ΦE =
∫
Ei •dAi
integral tertutup
Pernyataan Hukum Gauss:
net muatan
22
∫ E • dA =
Q
εo
permitivitas
Hukum Gauss Ù Hukum Coulomb
r
E
Q
dA
Q
∫ E • dA = ε
(Hukum Gauss)
o
Perhatikan untuk luasan yang berbentuk bola:
Karena
* E bukan fungsi luas dA
* E selalu tegak lurus dA
* E bernilai sama untuk setiap titik di permukaan bola
maka
Q
E ∫ dA =
εo
Q
E 4πr 2 =
εo
1 Q
E=
(Hukum Coulomb)
4 πε o r 2
Hukum Coulomb Æ hal khusus dari hukum Gauss
Aplikasi Hukum Gauss
(1) Untuk muatan pada kulit bola, hitung medan listrik
23
(a) di luar bola (b) di dalam bola
+ Q
+
+
+ kosong
+
+
+
+ R
r
+
+
+
E
(a) di luar bola
∫ E • dA =
Q
εo
Q
εo
Q
E 4πr 2 =
εo
1 Q
E=
4 πε o r 2
E ∫ dA =
(b) di dalam bola
∫ E • dA =
Q
εo
=0ÆE=0
24
(2) Untuk distribusi muatan pada bola padat
+
+ +
+ +
+ R
+
+ Q
+
+
+
+ +
+ +
r
+ + +
+
E
(a) di luar bola
Q
∫ E • dA = ε
o
Æ
E=
1 Q
4 πε o r 2
(b) di dalam bola?
ambil luasan bola di dalam bola bermuatan
Q'
E
•
d
A
=
∫
εo
disini Q' adalah muatan di dalam luasan bola yang diambil,
dapat dimengerti:
E
4 πr 3
r3
dalam
luasan
3
Q' =
Q=
Q=
Q
3
4 πR 3
Vtotal
R
3
r3 Q
1 Q
2
Æ E 4 πr =
Æ E=
r
3ε
3
πε
4
R o
o R
V
(linear)
r
R
25
(3) Kawat panjang
E
r
L
Q
∫ E • dA = ε
E2πrL=
Æ
E=
o
λL
εo
λ 1
2 πε o r
Hasil yang terakhir ini pernah kita peroleh dengan perhitungan
medan listrik dari kawat panjang via hukum Coulomb.
Tampak sekali bahwa perhitungan medan listrik menjadi sangat
sederhana apabila kita gunakan hukum Gauss.
Apa keterbatasan hukum Gauss?
Æ perhitungan medan listrik dengan cara ini menjadi sulit apabila
tidak ada luasan yang mempunyai simetri.
26