Thermodinamika

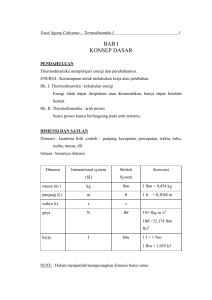
PANDANGAN UMUM TENTANG
THERMODINAMIKA
Thermodinamika adalah ilmu yang
membahas hubungan antara panas
dengan kerja. Hubungan ini didasarkan
pada
dua
hukum-hukum
dasar
thermodinamika,
yaitu
HUKUM
THERMODINAMIKA
PERTAMA
dan
HUKUM THERMODINAMIKA KEDUA.
PANDANGAN UMUM TENTANG
THERMODINAMIKA
Kedua hukum dasar ini akan dibicarakan
pada bab III dan bab V berikutnya.
Prinsif-prinsif
dan
metode-metode
thermodinamika
dipakai
pada
perencanaanperencanaan motor-motor bakar (Turbin), pusatpusat tenaga nuklir, pesawat-pesawat pendingin,
roket (pesawat terbang), pesawat-pesawat dengan
tenaga listrik dan lain-lain.
SISTEM THERMODINAMIKA
Pada
pelajaran
(pengetahuan)
thermodinamika,
benda
kerja
yang
dimaksudkan sering disebut dengan
sistem. Hal ini dimaksudkan untuk
memisahkan
benda
kerja
dengan
sekelilingnya (sekitarnya).
SISTEM THERMODINAMIKA
Adapun definisi dari sistem adalah :
suatu batasan yang dipakai untuk
menunjukan suatu benda (benda
kerja) dalam suatu permukaan
tertutup.
SISTEM THERMODINAMIKA
Misalnya :
*) Udara dikompresi di dalam silinder.
Dalam hal ini sistem adalah udara yang
dikompresikan dan permukaan tertutup
adalah permukaan yang dibatasi silinder
KOORDINAT SISTEM DAN KEADAAN SISTEM
Pada thermodinamika, volume V, temperatur T,
tekanan P, kerapatan ρ dan lain-lain disebut sebagai
koordinat sistem. Keadaan sistem tergantung pada
koordinat sistem, bila koordinat sistem berubah maka
keadaan sistem akan berubah. Sehingga koordinat
sistem sering disebut sebagai perubah (variabel)
keadaan sistem/zat.
Dimana perubahan keadaan
sistem dari suatu keadaan ke keadaan lain dapat
digambarkan pada diagram V, T, P.
KOORDINAT SISTEM DAN KEADAAN SISTEM
Dalam thermodinamika, besaran sistem dapat dibagi
menjadi dua besaran thermodinamika yaitu : besaran
Extensive dan besaran Intensive. Besaran extensive
dipengaruhi oleh massa atau mole sistem, sedangkan
besaran intensive tidak dipengaruhi oleh massa atau
mole sistem sistem.
Contoh :
Besaran extensive : Volume, Kapasitas Panas, Kerja (energi), entropy dll.
Besaran intensive : Tekanan, Temperatur, kerapatan dll.
KOORDINAT SISTEM DAN KEADAAN SISTEM
Dari besaran-besaran extensive akan
diperoleh harga-harga jenis (specific Value) dan hargaharga molar (molal specific value) dari suatu sistem,
seperti berikut :
*) Haraga Jenis (specific value) adalah
perbandingan antara besaran
extensive dengan massa sistem/zat.
Besaran extensive
H arg a Jenis 
massa sistem
KOORDINAT SISTEM DAN KEADAAN SISTEM
Contoh :
Volume jenis dari sistem:
V
v 
m
 m3

 kg
;
ft 3 

lb 
V = Volume sebenarnya (m3 ; ft3)
M = massa sistem (kg ; lb)
KOORDINAT SISTEM DAN KEADAAN SISTEM
**) Haraga jenis molar adalah perbandingan antara
besaran extensive dengan jumlah mole dari suatu
sistem/zat.
Contoh :
Volume Jenis Molar :
H arg a Jenis molar 
Dimana :
n
V
v* 
n
m
M
;
besaran extensive
jumlah mole sistem
 m3
ft3 


;
lb  mole 
 kg  mole


kg
lb

M  berat molekul sistem 
;
lb  mole 
 kg  mole
KOORDINAT SISTEM DAN KEADAAN SISTEM
Maka :
V
v* 
m/M
M .V
v* 
m
v*  M .v
KOORDINAT SISTEM DAN KEADAAN SISTEM
Untuk kerapatan suatu sistem/zat dapat dibuat
hubungan sebagai berikut :
 kg
 3 ;
m
m
1
 

V
v
Sehingga didapat :
v* 
M

lb 

3
ft 
TEKANAN (PRESSURE)
Bila permukaan suatu zat (padat, cair dan gas)
menerima gaya-gaya luar maka bagian permukaan zat
yang menerima gaya tegak lurus akan mengalami
tekanan (tertekan).
Gaya tegak lurus pada permukaan tersebut dibagi luas
permukaannya disebut Tekanan. Dengan rumus dapat
ditulis :
F
P
A
 kg
lb 
 2 ; 2 
ft 
m
Dimana :
F  gaya tegak lurus permukaan
kg
A  luas permukaan yang menerima gaya F
; lb 
m
2
;
ft 2

Dalam
thermodinamika,
tekanan
p
umumnya dinyatakan dalam harga absolut
(tekanan absolut/mutlak), maka dalam diktat ini
simbol p menyatakan tekanan absolut dari
sistem/zat
Tekanan absolut tergantung pada tekanan
pengukuran sistem, jadi:
1. Bila tekanan pengukuran (pressure gauge)
sistem diatas tekanan atmosfir, maka :
Tekanan absolut = Tekanan pengukuran + Tekanan Atmosfir
Atau :
Pabs = P gauge + P atm
2. Bila tekanan pengukuran (pressure gauge)
sistem di bawah tekanan atmosfir maka :
Tekanan absolut = Tekanan atmosfir – Tekanan pengukuran
Atau :
Pabs = Patm – Pgauge
Dalam satuan British, tekanan absolut dan
tekanan
pengukuran
masing-masing
dinyatakan dalam psia (pound persquare inch
absolut) dan psig (pound persquare inch
gauge).
1 standard atmosfir
= 1,01324 x 105 N/m2
= 14,7 lb/in2
= 10332 kg/m2
TEMPERATUR
HUBUNGAN
ANTARA
SKALA
RANKINE DAN
FAHRENHEIT
KELVIN,
CELCIUS,
Skala temperatur mutlak ada dua macam yakni :
Dalam satuan internasional
Tabs = 273 + T 0C (0K)
Dalam satuan British
Tabs = 460 + T 0F (0R)
Dimana :
T 0F = 9/5(T 0C) + 32
T 0C = 5/9(T 0F - 32)
Hubungan antara skala temperatur kelvin, celcius, rankine
dan fahrenheit
0R
672
492
0
0F
0K
0C
212
373
100
32
273
0
- 460
0
- 273
Ttk. didih
Ttk didih
Nol absolut
PERSAMAAN KEADAAN
PERSAMAAN KEADAAN GAS IDEAL (GAS SEMPURNA)
Dalam
thermodinamika,
gas
yang
dipergunakan sebagai benda kerja umumnya
semuanya dianggap bersifat sebagai gas ideal.
Hal ini disebabkan karena sifat-sifat gas ideal
hanya berbeda sedikit dari sifat-sifat gas yang
sebenarnya
Gas ideal (sempurna) adalah gas dimana
tenaga
ikat
molekul-molekulnya
dapat
diabaikan.
Jadi setiap gas Bila tenaga ikat
molekul-molekulnya dapat diabaikan tergolong
dalam gas ideal
Adapun persamaan gas ideal
satuan massa adalah sebagai berikut :
untuk
P.v = RT
Dimana :
P = Tekanan absolut (N/m2) ; lb/ft2 ; kg/m2)
v = volume jenis gas (m3/kg ; ft3/lb)
R = Konstanta gas (joule/kg-mole ; ft.lb/lb-mole)
T = Temperatur absolut gas (0K ; 0R)
Untuk massa m persamaan gas ideal dapat ditulis :
P.V = m.R.T
Dimana :
V = volume gas sebenarnya (m3 ; ft3)
M = massa gas (kg ; lb)
Untuk jumlah mole gas persamaan gas ideal menjadi :
Pv* = R0T
Atau :
PV = n.R0.T
Dimana :
n = jumlah mole gas (kg-mole ; lb-mole)
v* = volume jenis molar (m3/kg-mole ; ft3/lb-mole)
R0 = konstanta gas universil (joule/kg-mole.0K ; ft.lb/lbmole.0R)
Dengan:
R = R0/M
Dimana :
M = berat molekul gas (kg/kg-mole ;
lb/lb-mole)
Harga R0 adalah:
Nm
R0  8,3149.10
kg  mole.0 K
3
kg.m
R0  848
kg  mole.0 K
ft.lb
R0  1545,33
lb  mole.0 R
PERUBAHAN KEADAAN GAS IDEAL
Pada gas ideal terdapat
keadaan istimewa yaitu :
empat macam perubahan
1. Perubahan keadaan dengan proses
konstan (Isothermal/isothermis)
temperatur
P
Gas dimasukan kedalam silinder
torak. Keadaan gas akan dirubah
dari keadaan 1 ke keadaan 2
dengan menekan torak. Suhu
gas dijaga agar tetap konstan
dengan jalan mendinginkan dan
memanaskan silinder
2
T=konstan
1
V2
V1
V
P–V Diagram Proses Isothermal
2. Perubahan keadaan dengan proses volume
konstan (isometric ; isochoris)
P
2
P2
P1
1
V
V = konstan
P-V Diagram Proses Isochoris
keadaan gas dirubah
dari keadaan 1 ke
keadaan
2
dengan
memanaskan silinder,
sedang torak ditahan
supaya
jangan
bergerak
sehingga
volume
gas
dalam
silinder tetap konstan
3. Perubahan keadaan dengan proses tekanan konstan
(isobaric)
P
1
2
P1 = P2
V
V1
V2
P-V Diagram Proses Isobaric
Keadaan gas dirubah
dari keadaan 1 ke
keadaan 2 dengan
memanaskan silinder,
sedang torak dibuat
bebas
bergerak
sehingga tekanan gas
dalam silinder tetap
konstan
HUKUM THERMODINAMIKA PERTAMA
Bila kita berikan sejumlah panas kecil dQ
pada satu sistem, maka sistem tersebut akan
berekspansi dan melakukan kerja luar yang
kecil sebesar dW.
HUKUM THERMODINAMIKA PERTAMA
Tetapi disamping itu, pemanasan terhadap
sistem juga akan menimbulkan hal-hal :
1. Pertambahan kecepatan molekul dari
sistem.
2. Pertambahan jarak antara molekul-molekul
sistem karena sistem berekspansi.
HUKUM THERMODINAMIKA PERTAMA
Energi yang diperlukan untuk hal ini disebut
pertambahan energi dalam (internal energy).
Jadi panas dQ sebagian dirubah untuk
pertambahan energi dalam. Selain itu juga
sistem mengalami pertambahan energi kinetik
dan pertambahan energi potensial luar akibat
gaya-gaya konservatif luar seperti gaya gravitasi
dan lain-lain.
HUKUM THERMODINAMIKA PERTAMA
Bila kita buat :
dU = Pertambahan energi dalam
dEk = Pertambahan energi kinetik
dEp = Pertambahan energi potensial luar.
Maka dapatlah kita buat persamaan energi untuk
sistem tadi :
dQ = dW + dU + dEk + dEp
HUKUM THERMODINAMIKA PERTAMA
Persamaan ini menyatakan prinsip konservasi
energi dari suatu sistem dan menjadi hukum
thermodinamika pertama secara matematic.
Tapi
dalam
persoalan
thermodinamika,
sistem-sistem sebagian besar mengalami
energi kinetik dan energi potensial yang
konstan (pada sistem-sistem yang diisolasi)
atau dEk = 0 dan dEp = 0
HUKUM THERMODINAMIKA PERTAMA
Maka hukum thermodinamika pertama menjadi :
dQ = dU + dW
Bila kerja negative , berarti system menerima kerja
(kerja luar) dari sekelilingnya. Bila kerja positif , berarti
system melakukan kerja terhadap sekelilingnya. Untuk
menjelaskan hal ini marilah kita tinjau suatu silinder
berisi gas yang dilengkapi dengan torak yang dapat
bergerak
P
1
2
V1
dV
V2
V
ds
P-V Diagram, Kerja Gas dlm Silinder
Kerja Pada Perubahan Keadaan
Temperatur Konstan/isothermal
P
P1
Sistem
berubah
dari
keadaan 1 ke keadaan 2
dengan
temperatur
konstan.
T = konstan
T1 = T2
1
P2
2
V1
V2
V
V2
W  m.R.T .Ln
V1
Tekanan Konstan/isobaric
P
P1 = P2
1
V1
Sistem
berubah
dari
keadaan 1 ke keadaan 2
dengan tekanan konstan.
P = konstan
P1 = P2
2
V2
V
W = P(V2 – V1)
Volume Konstan W = 0 why?
PANAS JENIS (SPESIFIC HEAT)
Bila pada suatu sistem diberikan panas dQ
hingga menaikan temperatur sistem sebesar
dT, maka perbandingan panas dQ dengan
kenaikan temperatur dT disebut kapasitas
panas dari sistem.
Bila C adalah kapasitas panas dari sistem, maka :
dQ dU  dW
C

dT
dT
Bila proses berjalan dengan volume konstan,
maka kapasitas panas tersebut diatas disebut
dengan kapasitas panas pada volume konstan
disimbolkan dengan Cv. Selanjutnya bila
proses berjalan dengan tekanan konstan,
maka kapasitas panas tersebut disebut dengan
kapasitas panas pada tekanan konstan yang
disimbolkan dengan Cp.
Kapasitas panas C persatuan massa m
disebut panas jenis (specific heat) disimbol
dengan c, jadi panas jenis suatu sistem
adalah :
C
dQ
c 
m m.dT
Panas yang masuk kesistem persatuan massa
untuk perubahan temperatur dT, besarnya :
dq = c.dT
Untuk proses dengan volume konstan :
dq = du = cv.dT
Untuk proses dengan tekanan konstan :
dq = cp.dT
Panas total yang masuk kesistem (untuk massa m),
besarnya :
dQ = m.dq = m.cp.dT
atau :
T2
Q  m  c p .dT
T1
Bila cp konstan, maka :
Q = m.cp (T2 – T1)
Untuk proses dengan volume konstan :
Q = U2 – U1 = m cv (T2 – T1)
Untuk semua gas dapat ditulis :
cp – cv = R
dimana : cp/cv = γ , maka :
cv = R / (γ – 1)
cp = γ.R / (γ – 1)
PENGGUNAAN HUKUM THERMODINAMIKA
PERTAMA
PROSES ADIABATIK
Perubahan keadaan disebut adiabatik bila tidak
ada panas yang dikeluarkan/diterima sistem
dari/terhadap sekelilingnya atau dq = 0.
PENGGUNAAN HUKUM
THERMODINAMIKA PERTAMA
Hal ini dimungkinkan bila sistem diisolasi.
Kejadian ini terjadi pada motor-motor bakar
jenis diesel, pada akhir kompresi temperatur
udara
sangat
tinggi
hingga
sanggup
membakar bahan bakar tanpa menggunakan
bunga api.
Pandang suatu silinder berisolasi berisi gas yang dilengkapi
dengan piston seperti terlihat pada gambar berikut :
Hukum thermodinamika pertama
dq = du + dw
0 = du + dw
atau
U2 – U1 = - W
U1 – U2 = W
P-V Diagram Proses Adiabatik
Kerja pada proses Adiabatik
Pada proses Ekspansi Adiabatik
1
W
( P1V1  P2V2 )
 1
Pada proses kompresi Adiabatik
1
W
( P2V2  P1V1 )
 1
ENTALPY
Entalpy suatu sistem adalah penjumlahan dari energi dalam
dengan hasil kali tekanan dan volume sistem.
H = U + P.V
Q = H 2 – H1
H2 – H1 = m.cp(T2 – T1)
h2 – h1 = cp(T2 – T1)
PROSES MELINGKAR CARNOT
1-2 . Ekspansi isothermal
2-3. Ekspansi adiabatik
3-4. Kompresi isothermal
4-1. Kompresi adiabatik
Kerja pada proses ekspansi isothermal 1-2 :
 V2
W1   P.dV  m.R.T2 .Ln
 V1
v1
v2



Kerja pada proses ekspansi adiabatik 2-3 (dQ = 0 ; dW = - dU) :
3
T1
2
T2
W2   dU  m  cv dT  m.cv (T1  T2 )  m.cv (T2  T1 )
Kerja pada proses kompresi isothermal 3-4 :
 V4 
W3   P.dV  m.R.T1 .Ln 
 V3 
v3
v4
Kerja pada proses kompresi adiabatik 4-1 :
1
T2
4
T1
W4   dU  m  cv dT  m.cv (T2  T1 )
Pada proses ekspansi isothermal 1-2 dan proses
kompresi isothermal 3-4, energi dalam gas ideal
adalah konstan, maka :
W2 = Q2 ; W1 = Q1
Dengan demikian kerja netto pada proses melingkar
carnot menjadi :
W = Q2 – Q1
Efisiensi thermis dari lingkaran carnot adalah :
W Q2  Q1
t 

Q2
Q2
T2  T1
t 
T2
Dari kedua persamaan diatas didapat hubungan :
Q1 T1

Q2 T2
Skema diagram alir untuk mesin panas carnot
REFRIGERATOR (PENDINGIN) CARNOT
Karena proses melingkar carnot
reversibel, maka proses dapat dibalik
adalah
proses
Proses yang dibalik ini disebut dengan refrigerator
carnot. Jadi refrigerator carnot bekerja dengan
kebalikan dari mesin panas carnot. Mesin carnot disebut
dengan direct cycle sedang refrigerator carnot disebut
reversed cycle
Refrigerator carnot menerima kerja luar W dan
menyerap panas Q1 dari reservoar dingin (heat sink)
temperatur T1 serta memberikan panas Q2 ke reservoar
panas temperatur T2
Skema diagram alir Refrigerator carnot
Jadi dapat dibuat hubungan :
W = Q2 – Q1
Koefisien of Performan :
Q1
Q1
T1
c


W Q2  Q1 T2  T1