kuliah - xiv

KULIAH - XIV
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
1
BAB IV
HUKUM TERMODINAMIKA II
Hukum Termodinamika I adalah :
- Menetapkan adanya suatu ekivalensi antara panas dan kerja (panas ↔ kerja)
- Digunakan untuk menghubungkan dan menentukan type – type energi yang terlibat
dalam suatu proses.
- atau menyatakan bahwa sewaktu proses berlangsung terdapat suatu keseimbangan
energi.
Hukum termodinamika I merupakan pernyataan dari hukum kekekalan energi dan tidak
menyatakan sesuatu apapun mengenai arah dari proses yang berlangsung.
Proses termodinamika itu dapat berlangsung kedua arah yaitu :
- Diekspansikan (pengembangan)
- Dikompresikan (penekanan)
Hukum Termodinamika I juga belum menjelaskan kearah mana suatu perubahan keadaan
itu berjalan dan apakah perubahan itu reversible atau irreversible.
→ Dalam pengembangannya diterangkan dan dibahas dalam Hukum Termodinamika II
MHZ
2
Jadi : Hukum Termodinamika II, memberikan batasan-batasan tentang arah yang dijalani
suatu proses, dan memberikan kriteria apakah proses itu reversible atau irreversible dan
salah satu akibat dari Hukum Termodinamika II ialah perkembangan dari suatu sifat phisik
alam yang disebut ENTROPI.
Perubahan entropi → menentukan arah yang dijalani suatu proses.
Hukum Termodinamika II menyatakan :
* Tidak mungkin panas dapat dirubah menjadi kerja seluruhnya, tetapi sebaliknya kerja
dapat dirubah menjadi panas.
atau :
Q ≠ W seluruhnya
W → Q (sama besarnya)
atau untuk mendapatkan sejumlah kerja (W) dari suatu siklus, maka kalor (Q) yang harus
diberikan kepada sistem selalu lebih besar.
→ Q diserap > W
sehingga, η siklus < 100 %.
* Suatu yang bekerja sebagai sebagai suatu siklus tidak dapat memindahkan kalor (Q) dari
bagian yang bertemperatur rendah ke bagian yang bertemperatur lebih tinggi, tanpa
menimbulkan perubahan keadaan pada sistem yang lain.
MHZ
3
Dari kedua hal tersebut diatas, menyatakan tentang arah proses perubahan energi dalam
dalam bentuk panas ke bentuk kerja → yang menyatakan adanya pembatasan transformasi
energi.
MHZ
4
KULIAH - XV
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
5
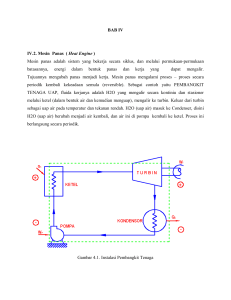
Mesin Panas
( Heat Engine )
Mesin panas adalah sistem yang bekerja secara siklus, dan melalui
permukaan-permukaan batasannya, energi dalam bentuk panas dan kerja
yang dapat mengalir.
Tujuannya mengubah panas menjadi kerja. Mesin panas mengalami proses
– proses secara periodik kembali kekeadaan semula (reversible). Sebagai
contoh yaitu PEMBANGKIT TENAGA UAP, fluida kerjanya adalah H2O yang
mengalir secara kontiniu dan stasioner melalui : Ketel (dalam bentuk air dan
kemudian menguap), mengalir ke Turbin. Keluar dari turbin sebagai uap air
pada temperatur dan tekanan rendah. H2O (uap air) masuk ke Condenser,
disini H2O (uap air) berubah menjadi air kembali, dan air ini di pompa
kembali ke ketel. Proses ini berlangsung secara periodik.
MHZ
6
Menurut Hukum Termodinamika I :
atau
MHZ
φ dQ = φ dW
Qk − Qc = WT − WP
7
Maka, Effisiensi Termik dari siklus tertutup ini adalah :
η th =
Q
WT − WP QK − QC
=
= 1− C
QK
QK
QK
Disini dapat dilihat bahwa, sistem menerima panas pada temperatur tinggi, kemudian
panas dibuang oleh sistem temperatur rendah, dan kerja dilakukan pada lingkungan.
Kita ambil “dua mesin pemanas”, yang tujuan utamanya adalah mengubah panas
menjadi kerja, dan melakukan kerja pada lingkungan.
MHZ
Gambar mesin panas dan pompa panas
8
Untuk mesin panas :
Wout = Qin − Qout
Wout + Qout = Qin
η th =
Wout
Q − Qout
Q
= in
= 1 − uot
Qin
Qin
Qin
Untuk pompa panas :
Win = Qout − Qin
Win + Qin = Qout
koefisien prestasi =
( KP) pompa panas =
Qout
Qout
=
=
Win
Qout − Qin
( KP ) me sin pendingin =
( KP ) me sin pendingin =
MHZ
efek energi yang dituju
pemasukan energi yang diperlukan
1
Q
1 − in
Qout
efek energi yang dituju (efek pendinginan)
pemasukan energi yang diperlukan
Qin
=
Qout − Qin
1
Qin
−1
Qout
9
Contoh Soal
1. Panas yang digunakan oleh suatu mesin panas adalah : 1150 Kj/mnt dan mesin
menghasilkan 7,5 Kw
Ditanya :
Jawab :
a.
ηth =
a.
η th = ........ ?
b.
Qout = ........ ?
Qin = 1150 kJ/mnt
Wout = 7,5 kW = 7,5(60) = 450 kJ/mnt
450
kJ / mnt
1150
b. Qout = Qin − Qout
MHZ
= 0,391 (39,1%)
= ( 1150 – 450 ) kJ/mnt
= 700 kJ/mnt
10
2. Sebuah bangunan memerlukan panas : 100.000 Kj/mnt dari suatu pompa panas yang
menyerap panas dari udara dingin diluar dan memberikannya ke ruangan – ruangan
bangunan tersebut. untuk menjalankan pompa diperlukan kerja :14.800 Kj.
Ditanya :
a) Besarnya panas yang diserap dari udara luar (Qin)
b) (KP) pompa panas
Jawab : Qout
= 100.000 kJ/mnt
a) Jumlah panas yang diperlukan pompa panas :
Qout − Qin = 14.800 kJ / mnt
jadi :
Qin = 85.200 kJ/mnt
b) Koefisien Panas pompa panas =
MHZ
Qout
Qout − Qin
=
100.000 kJ / mnt
= 6,75
14.800 kJ / mnt
11
KULIAH - XVI
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
12
KEGUNAAN HUKUM TERMODINAMIKA II
1. Menentukan effisiensi paling tinggi dari mesin panas atau KP yang maximum dari
mesin pendingin.
2. Menentukan apakah proses dapat berlangsung atau tidak (irreversible atau
reversible).
3. Menentukan arah atau derajat suatu reaksi kimia.
4. Menentukan skala temperaturyang tidak tergantung pada sifat-sifat fisik tiap zat.
5. Mendefinisikan suatu sifat yang sangat berguna.
PROSES REVERSIBEL
1. Gerakan relative tanpa gesekan (licin)
2. Peregangan dan penekanan suatu pegas.
3. Ekspansi dan kompresi adiabatik tanpa gesekan.
4. Ekspansi dan kompresi isotermik
5. Ekspansi dan kompresipolintropik.
6. Elektrolisa
MHZ
13
PROSES IRREVERSIBEL
1. Gerakan relatif dengan gesekan.
2. Ekspansi bebas (tidak ada kerja karena Q = 0 → U = 0 )
3. Pembakaran.
4. Proses difusi.
SIKLUS REVERSIBEL : SIKLUS CARNOT
Siklus carnot ini terdiri dari : - 2 proses isotermik
- 2 proses adiabatik reversibel
Siklus carnot : Memiliki medium kerja yang menerima panas dari suatu temperatur dan
melepaskannya pada temperatur yang lain → jadi diperlukan dua reservoir yang
berdasarkan hukum termodinamika kedua merupakan jumlah minimum.
Siklus ini dapat terjadi pada proses-proses tak mengalir reversibel atau pada prosesproses stasioner.
MHZ
14
Siklus Carnot pada diagram P-V :
Karena sistem mengalami satu siklus maka energi dalam tidak berubah, jadi ∆U = 0.
Maka Hukum Termodinamika I diperoleh:
φ dQ = φ dW = Q2 − Q1
dimana :
MHZ
W adalah kerja total
Q2 panas yang diserap sistem
Q1 panas yang dilepaskan oleh sistem
15
Maka effisiensi temik siklus carnot, yaitu hasil bagi kerja yang dilakukan sistemdengan
panas yang diserap sistem pada temperatur tinggi :
v=
V
m
η =
φ dW
Q2
=
Q2 − Q1
Q
= 1− 1
Q2
Q2
Contoh:
Perhitungan effisiensi termik mesin carnot yang menggunakan gas ideal :
Jawab:
untuk gas ideal: PV = mRT atau pv = RT
du = Cv . dT
- Proses 1-2 : proses isotermik, pv = konstan.
MHZ
16
2
Wda =
∫ pdV = p1v1 ln
1
q = w = p1v1 ln
p1
p2
q = w = RT1 ln
p1
p2
v2
p
= p1v1 ln 1
v1
p2
- Proses 2-3 : proses adiabatik reversible, pvγ = konstan, dq = 0.
W = - ∆U = - Cv (T3 – T2) atau W = - ∆U = - Cv (T1 – T2)
W = - ∆U = Cv (T2 – T1)
W = - ∆U = Cv (T2 – T1)
- Proses 3-4 : Proses isotermik ; ∆U = 0
 p4

pdV
=
−
p
v
ln
3 3
∫3
 p3
4
Wda =
p 
q = w = − p3 v3 ln  4 
 p3 
MHZ



p 
= − RT3 ln  4 
 p3 
17
- Proses 4-1 : Adiabatik reversible dq = 0 , pvγ = konstan
w = - ∆U = - Cv (T1 – T4)
atau w = - Cv (T2 – T1)
w = Cv (T1 – T2)
→ Jadi jumlah kerja siklus :
φ dQ = φ dW
φ dW = q1− 2 − q3−4
 p1
 p2
φ dW = RT2 ln 
p 

 − RT1 ln  4 

 p3 
→ Untuk proses adiabatik :
γ
p 2  T2  γ −1
=  
p3  T3 
p1  T1 
= 
p 4  T4 
MHZ
γ
γ −1
18
p2
p
= 1
p3
p4
atau
p4
p
= 1
p3
p2
φ dW = RT2 ln
η th =
MHZ
φ dw
q1− 2
p1
p
p
− RT1 ln 1 = R(T2 − T1 ) ln 1
p2
p2
p2
R (T2 − T1 ) ln
=
RT ln
p1
p2
p1
p2
=
T2 − T1
T2
19
Jadi η Carnot hanya bergantung pada T1 dan T2.
Maka akan diperoleh ; effisiensi carnot adalah:
η =
Q2 − Q1
T −T
= 2 1
Q2
T2
η = 1−
Q1
T
= 1− 1
Q2
T2
Q2
Q1
=
T2
T1
atau:
Q2
T2
MHZ
=
Q1
T1
20
KULIAH - XVII
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
21
”ENTROPI”
- Hukum Termodinamika II dalam bentuk ketidaksamaan clasius mengenai entropi
- Dari proses reversibel siklus carnot diketahui :
Q2
=
T2
Q1
T1
dimana : Q2 = panas masuk sistem (+)
Q1 = panas keluar sistem (-)
Persamaan diatas ditulis :
Q2
atau :
T2
+
Q2
T2
= −
Q1
T1
Q1
ΣQ
=
=0
T1
T
Persamaan diatas untuk proses reversibel siklus carnot dapat ditulis:
φ rev
MHZ
dQ
T
=0
22
Untuk suatu siklus yang irreversibel integral siklus ini akan lebih kecil dari nol dan dapat
ditulis sebagai;
φirrev
dQ
<0
T
Persamaan diatas dapat ditulis sebagai berikut :
φ
dQ
≤0
T
besaran
dQ
T
Ketidaksamaan clausius
merupakan parameter sistem dan disebut “ENTROPI”
ENTROPI adalah perbandingan panas yang ditransfer selama proses reversibel dengan
temperatur absolut sistem.
MHZ
23
Contoh soal :
Sebuah mesin uap bekerja diantara sebuah ketel pada temperatur tetap 3280 F, dan
sebuah kondensator dengan temperatur 1260 F. Air masuk kedalam ketel dalam
keadaan cair jenuh. tunjukkanlah bahwa berlaku ketidaksamaan clausius untuk siklus ini.
Jawab :
Perpindahan panas terjadi dalam ketel dan kondensor
Ketel :
q k = h2 − h1
q k = 1187 − 298 = 889 BTU
MHZ
Lbm
24
Kondensor
q k = h4 − h3
q k = 196 − 1014 = − 818 BTU
Lbm
Jadi Integral siklus :
φ
q
dq q k
889 818
=
+ c =
+
= − 0,26 BTU
lbm, o R
T
T
T
788 586
→ Berlaku ketidaksamaan Clausius.
MHZ
25
Jadi entropi merupakan perbandingan panas yang ditransfer selama proses reversibel
dengan temperatur absolut siklus.
 dQ 
ds = 

 T  rev
Secara matematis
atau :
 dQ 
∆s = ∫ 

 T  rev
2
 dQ 
S 2 − S1 = ∫ 

T  rev
1 
→ Perubahan Entropi dari keadaan 1 ke keadaan 2
MHZ
26
KULIAH - XVIII
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
27
PERHITUNGAN PERUBAHAN ENTROPI
2
Perubahan Entropi
 dQ 
∆s = ∫ 

T

 rev
1
 dU + dW 
 dQ 
∆s = ∫ 

 = ∫
T
 T  rev

 rev
T ds = dU + p dV
dimana :
H = U + pV
U = H – pV
T ds = d ( H − pV ) + p dV
T ds = dH − p dV
Satuan Entropi
{
(Entropi persatuan massa)
MHZ
}{
S = Btu 0 ; Kal
gr : K
lbm R
{
S = Btu
0
}
}
; {Kal }
K
R
T ds = dH − V dp
28
Untuk satu satuan massa :
T ds = dh + v dp
Contoh:
Hitunglah perubahan entropi untuk 3 kg gas ideal dengan Cv = (18,94+0,0528 T) kg/kg
K, selam proses volume tetap dari 75o C sampai 100o C.
Jawab :
Untuk gas ideal : PV = RT, du = Cv . dT
dalam satu satuan massa : Tds = du + pdv
Tds = Cv.dT + pdv
ds = cv
; ( pdv = 0 )
dv
dT
P
dT
+ dv = cv
+R
T
T
T
v
T2
s 2 − s1 =
∫
T1
cv
v
dT
+ R . ln 2
T
v1
→ R . ln
v2
= 0 ; karena v = kons tan
v1
T2
s 2 − s1 =
dT
(
)
18
,
94
+
0
,
0528
T
∫
T1
MHZ
T
29
s 2 − s1 = 18,94 ln
s 2 − s1 = 2,627 KJ
Untuk 3 kg, maka :
MHZ
373
+ 0,0528 (373 − 348)
348
kg K
∆S = 3 (2,627) = 7,881 KJ
kg
30
DIAGRAM TEMPERATUR – ENTROPI
Dari persamaan :
atau
dS =
dQ
T
dQ = T ds
s2
Q1− 2 =
∫ T dS
s1
2
W12 = ∫ p dv
1
MHZ
2
Q12 = ∫ T ds
1
31
φ dW = φ dQ
φ p dV = φ T dS
Diagram P-V dan T-S menyatakan proses reversibel dapat kita ambil contoh pada
proses / siklus carnot, sebagai berikut :
MHZ
32
Garis 1-2 dan 3-4 : proses isotermik (dT = 0)
Garis 2-3 dan 4-1 : proses adiabatik reversibel (dQ = 0 = T dS) ; T ≠ 0 ; dS = 0
Jadi, adiabatik reversibel = isontropik (entropi konstan)
Effisiensi siklus carnot dapat dihitung dari diagram T-S :
η th =
η th =
MHZ
φ dw
Qin
=
Qin − Qout
T ( s − s ) − T1 ( s 2 − s1 )
= 2 2 1
Qin
T2 ( s 2 − s1 )
T2 − T1
T
= 1− 1
T2
T2
33
KULIAH - XIX
TERMODINAMIKA TEKNIK I
TKM 203 (4 SKS)
SEMESTER III
DEPARTEMEN TEKNIK MESIN
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
TAHUN 2006
MHZ
34
AZAS PERTAMBAHAN ENTROPI
∆S S + ∆S L = ∆S KS
∆S SK = ∆S System + ∆S Lingkungan ≥ 0 (untuk proses reversibel dan irreversibel)
Bila sistem diisolasi, maka tidak ada hubungan energi dengan lingkungan, sehingga
entropinya tetap.
∆S LING = 0
∆S SK = ∆S SYS ≥ 0
MHZ
35
ENERGI YANG HILANG PADA PROSES
Sebagai contoh pada siklus carnot :
Effisiensi siklus carnot dan hubungannya dengan temperatur :
η th =
T −T
W
= 2 1
Q
T2
 Qin − Qout

 Qin
MHZ
  Tin − Tout
 = 
  Tin



36
Jumlah kerja yang diperoleh :
T − T 
 T 
W = Q  2 1  = Q 1 − 1 
 T2 
 T2 
W = Q − T1 ∆S
Q
= Energi yang masuk T1 ∆S
T1 ∆S = Energi yang hilang
MHZ
37