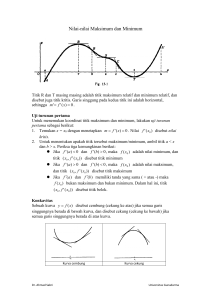
9.2 Maksimum dan Minimum Relatif : Uji Derivatif-Pertama

9.1 Nilai Optimum dan Nilai Ekstrem
Dalam ilmu ekonomi kita mengenal tentang maksiminasi
dan minimasi dengan istilah umum optimasi, yang berarti
“mencari yang terbaik” . Akan tetapi hal ini berbanding
terbalik karena istilah tersebut tidak memiliki kaitannya
dengan matematika murni. Oleh karena itu, istilah kolektif
untuk maksimum dan minimum sebagai konsep matematik
ialah nilai ekstremum, yang berarti nilai ekstrem
9.2 Maksimum dan Minimum Relatif : Uji Derivatif-Pertama
Ekstrem Relativ Vs Absolut
Maksimum absolut pasti merupakan maksimum relatif atau salah satu
titik akhir fungsi . Jadi, bila kita mengetahui semua maksimum relatif, maka kita
hanya perlu memilih yang terbesar dan membandingkannya dengan titik akhir
guna menentukan maksimum absolut
.Selanjutnya, nilai-nilai ekstrem yang dipertimbangkan akan
merupakan ekstrem relatif atau ekstrem lokal, kecuali bila
ditentukan lain.
Uji Derivatif-Pertama
Derivatif pertama adalah turunan pertama suatu fungsi. Misal
fungsi y=f(x), maka f’(x) digunakan dalam mencari nilai ekstrem.
Uji derivatif pertama untuk ekstrem relatif. Jika derivatif pertama pada
fungsi f(x) pada x=x0 adalah f’(x0) = 0, maka nilai fungsi x0,f’(x0)
merupakan
a. Maksimum relatif jika f’(x) berubah tanda dari positif ke negatif dari
sebelah kiri titik x0 ke sebelah kanannya
b. Minimum relatif jika f’(x) berubah tanda dari negatif ke positif dari
sebelah kiri titik x0 ke sebelah kanannya
c. Tidak maksimum maupun minimum relatif bila f’(x) mempunyai
tanda yang sama baik sebelah kiri maupun sebelah kanan titik x0
9.3 Derivatif Kedua dan Derivatif yang Lebih Tinggi
Contoh derivatif pertama sampai kelima suatu fungsi:
Contoh derivatif pertama sampai keempat suatu fungsi
rasional:
9.4
Uji Derivatif Kedua
a) x = x0 merupakan titik relatif maksimum jika f "( x ) < 0
b) x = x0 merupakan titik relatif minimum jika f "( x ) > 0
c) x = x0 tidak dapat disimpulkan secara pasti atau uji derivatif kedua
gagal jika f "( x ) = 0
Cara menguji kecekungan adalah sbb :
a) Jika f "( x ) < 0 maka fungsi cekung ke bawah (concave)
b) Jika f "( x ) > 0 maka fungsi cekung ke atas (convex)
Titik belok (inflection point) adalah suatu titik dimana kecekungan
berubah.
Cara mencari titik belok adalah mencari solusi dari f "( x ) = 0
Tabel kondisi relative ekstremum : y = f ( x )
9.5
Deret Maclaurin
Deret MacLaurin adalah sebuah fungsi yang dapat
dinyatakan dalam bentuk deret polinomial
Tapi tidak semua fungsi bisa dinyatakan dalam bentuk
tersebut, contohnya
Untuk itu, Taylor membuat deret yang lebih
umum,Deret taylor merupakan derivatif dari Deret
Maclaurin. Dapat ditulis dengan
Teorema Taylor dapat ditulis :
Rn = F (n+1)(C) (X-X0 )n+1
(n+1)!
Untuk suatu c diantara x dan x0 . Formula Rn disebut
bentuk Lagrange (atau bentuk derivatif) dari sisa
11.1 Versi Diferensial dari Syarat Optimisasi
Syarat Orde Pertama :
Jika diketahui fungsi z=f(x), kita dapat menulis diferensial dz= f’(x) dx
Kondisi derivatif orde pertama “f’(x) = 0” dapat diubah dalam kondisi
diferensial orde pertama ; “dz = 0 untuk sembarang nilai dx yang tidak nol”.
Syarat Orde Kedua :
Syarat cukup orde kedua untuk titik ekstrem z adalah, dalam istilah derivatif,
f”(x) < 0 (untuk suatu maksimum) dan f”(x) > 0 (untuk suatu minimum) pada
titik stasioner.
d2x d(dz) = d[f’(x) dx]
= [df’(x)] dx
=[f”(x) dx] dx = f”(x) dx2
Dapat diterjemahkan masing – masing, menjadi untuk
sembarang nilai.
dx ≠ 0
Syarat Diferensial versus Syarat Derivatif
Secara lebih spesifik, syarat orde nilai pertama(nilai dz yang
sama dengan nol) dan syarat orde kedua (untuk d2x negatif atau
positif) dapat digunakan dengan validitas yang sama untuk semua
kasus yang diberikan dengan umgkapan “untuk sembarang nilai dx
yang tidak sama dengan nol” yang harus dimodifikasi untuk
menggambarkan perubahan jumah variabel pilihan.
11.2 Nilai Ekstrem fungsi dua variabel
Syarat Orde 1
• Suatu fungsi 2 peubah memiliki nilai maksimum
relatif pd titik (xo, yo) jika terdapat lingkaran
berpusat di (xo, yo) s.d.h utk setiap (x, y) di dlm
lingkaran dan f memiliki nilai maksimum mutlak
di (xo, yo) bila utk semua titik (x, y) di domain f
• Jika f memiliki nilai ekstrim relatif pada titik (xo,
yo) dan bila turunan parsialnya ada pada titik tsb
maka fx (xo , yo ) = 0 dan f y (xo , yo ) = 0
Syarat Orde 2
Misal f fungsi 2 peubah dg turunan parsial orde 2 kontinu
dalam beberapa lingkaran pada titik kritis (xo, yo) dan
misalkan D = f xx (xo , yo ) f yy (xo , yo )− f xy 2 (xo , yo )
a. Jika D > 0 dan f xx (xo , yo ) > 0 , maka f punya minimum
relative
b. Jika D > 0 dan f xx (xo , yo ) < 0 ,maka f punya maksimum
relatif
c. If D < 0 , maka f memiliki titik pelana (a saddle point)
d. If D = 0 , maka tdk ada kesimpulan yg dpt digambarkan
11.3 Bentuk Kuadrat – Suatu Ekskursi
Setiap suku mempunyai derajat yang sama- yaitu, dimana
jumlah eksponen dalam setiap suku sama, plinom ini disebut sebagi
suatu bentuk (form). Misal :
4x – 9y + z adalah bentuk linear dalam tiga varibel
4x2 – xy + 3y2 adalah bentuk kuadrat dalam 2 variabel
Kita juga akan menjupai kuadrat dalam tiga variabel seperti x2 +
2xy – yw + 7w2, atau juga dalam n variabel
Diferensial Total Orde Kedua sebagai Suatu Bentuk Kuadrat
Q = au2 + 2huv + bv2
dx = u
dy = v
Variabel
11.4 Fungsi Tujuan dengan Lebih dari Dua Variabel
Syarat Orde Pertama untuk Titik Ekstrem
Pembahasan sebelumnya menyatakan bahwa, untuk
memperoleh suatu maximum atau minimum dari z
diperlukan dz = 0 untuk sembarang nilai dx1, dx2, dan
dx3 tidak nol. Karena nilai dz sekarang
dz= f1 dx1 + f2 dx2 + f3 dx3 , f1 = f2 = f3 = 0
Jadi, syarat perlu untuk titik ekstrem adalah, bahwa
semua derivative parsial orde pertama adalah nol, sama
seperti untuk kasus dua variable
Syarat Orde Kedua
d2z = d (dz) = f11 dx12 dx1 + f12 dx1 dx2 + f13 dx1 dx3 + f21 dx2
dx1 + f22 dx + f23 dx2 dx3 + f31 dx3 dx1 + f32 dx3 dx2 + f33 dx
=|H| yang minor utamanya bisa
dinyatakan sbb |H1| = f11 |H2| = |H3| = |H|
Jadi, berdasarkan criteria determinan untuk kedefinitan
p[ositif dan negative, kita dapat menyatakan syarat cukup orde
kedua untuk suatu titik ekstrem dari z sebagai berikut
Z* adalah suatu bila d2z definit negative atau d2z definit positif
Kasus n-Variabel
Z= f (x1, x2, … , xn) diferensial totalnya akan menjadi
dz = f1 dx1 + f2 dx2 + … + fn dxn
Sehingga syarat perlu untuk titik ekstrem (dz = 0
untuk sembarang dz, tidak semuanya nol) berarti
bahwa semua n dserivatif positif parsial orde
pertama harus sama dengan nol
11.5 Syarat orde kedua dalam hubungannya dengan
kecembungan dan kecekungan
Z* = f(x*1 ,……x*n)
d2z adalah definit
negatif pada z*
(syarat cukup orde
kedua)
F adalah
cekung
d2z adalah
Definit negatif
dimana saja
d2z semi definit
negatif pada z*
(syarat perlu orde
kedua)
z* adalah maksimum
relatif
F adalah
cekung
sempurna
z* adalah maksimum
absolut
z* adalah maksimum
absolut yang tunggal
Pengecekan kecembungan dan kecekungan
Suatu fungsi f adalah (cembung atau cekung) bila, untuk
setiap pasangan titik u dan v yang berbeda dalam domain f,
dan untuk 0 < 0 < 1
Dalil untuk fungsi-fungsi dengan jumlah berapapun :
Dalil I (fungsi linear) :
jika f(x) = fungsi linear, maka f(x) = fungsi cekung dan juga
fungsi cembung, tetapi tidak sempurna
Dalil II (negatif dari suatu fungsi) :
jika f(x) fungsi cekung, maka f(x) adalah fungsi cembung, dsb,
demikian juga, bila f(x) = fungsi cekung sempurna, maka f(x) adalah
fungsi cembung sempurna, dsb.
Dalil III (jumlah dari suatu fungsi) :
jika f(x) dan g(x) kedua-duanya = fungsi cekung (cembung),
maka f(x) + g(x) juga merupakan fungsi cekung (cembung) dan bila
satu atau keduanya cekung sempurna (cembung sempurna), maka
f(x) + g(x) adalah cekung sempurna (cembung sempurna)
Fungsi yang dapat dideferensialkan
Fungsi yang dapat dideferenialkan (fx) adalah (cekung, cembung)
jika, untuk setiap titik tertentu u dan setiap titik lain v domain.
Fungsi Cembung vs Himpunan Cembung
Kombinasi linear dari dua vektor u dan v dapat ditulis sebagai
K1u + k2v, dimana k1 dan k2 adalah dua skalar
Oquv membentujk jajaran genjang, maka diperoleh
u = q + v atau q = u – v
Kombinasi cembung dari vektor u dan v dapat dinyatakan delam bentuk
vektor q
W = Ɵu + (1-Ɵ)v = Ɵu + v – Ɵv = Ɵ(u –v) +v = Ɵq + v
11.6 Penerapan Ekonomi
PERMASALAHAN PERUSAHAAN MULTI PRODUK
Ausmsikan bahwa perusahaan dengan dua produk berada pada keadaan
persaingan sempurna Maka,
fungsi pendapatannya akan menjadi :
Dengan menetapkan keduanya
R1 = P10Q1 +P20Q2
sama dengan nol,maka :
P = harga
Qi = tingkat output produk ke-i
Fungsi biaya perusahaan :
C = 2Q12 + Q1Q2 + 2Q22
Fungsi laba perusahaan :
Mencari tingkat Q1 dan Q2 yang,dalam
kombinasi,akan memaksimumkan π :
Yang menghasilkan pemecahan
tunggal :
DISKRIMINASI HARGA
Fungsi pendapatan total dan fungsi biaya total :
R = R1(Q1) + R2(Q2) + R3(Q3)
C = C(Q) dimana Q = Q1 +Q 2+ Q3
KEPUTUSAN INPUT DALAM PERUSAHAAN :
L* dan K* adalah persamaan permintaan input perusahaan.
Jika kita substitusikan L* dan K* ke dalam fungsi produksi ,kita peroleh :
Fungsi yang data didiferensikan f(x)=
f(x1 ,…,Xn) adalah (cekung cembung)
jika, untuk setiantitik tertentu u= (U1
,…,Un) dan setiap titik lain v= (V1
,…,Vn) dalam domain,
F(v) () f(u) + Σ fj (u) (Vj - Uj )
Dimana fj (u) ≡∂f/ ∂ Xj dievaluasi pada
u= (U1 ,…,Un)
11.7
B
y
F(v)
C
A
F
D
)
F(u
u
v
X
Fungsi z data didiferensiasikan dua
kali secara kontinu z= f(x1 ,…,Xn)
adalah (cekung/cembung) jika, dan
hanya jika, d2 z di mana saja adalah
semidefinit (negative/positif). Fungsi
tersebut dikatakan (cekung/cembung)
sempurna jika (tetapi tidak hanya jika)
d2 z dimana saja adalah definit
(negative/positif).