Listrik Bolak-Balik

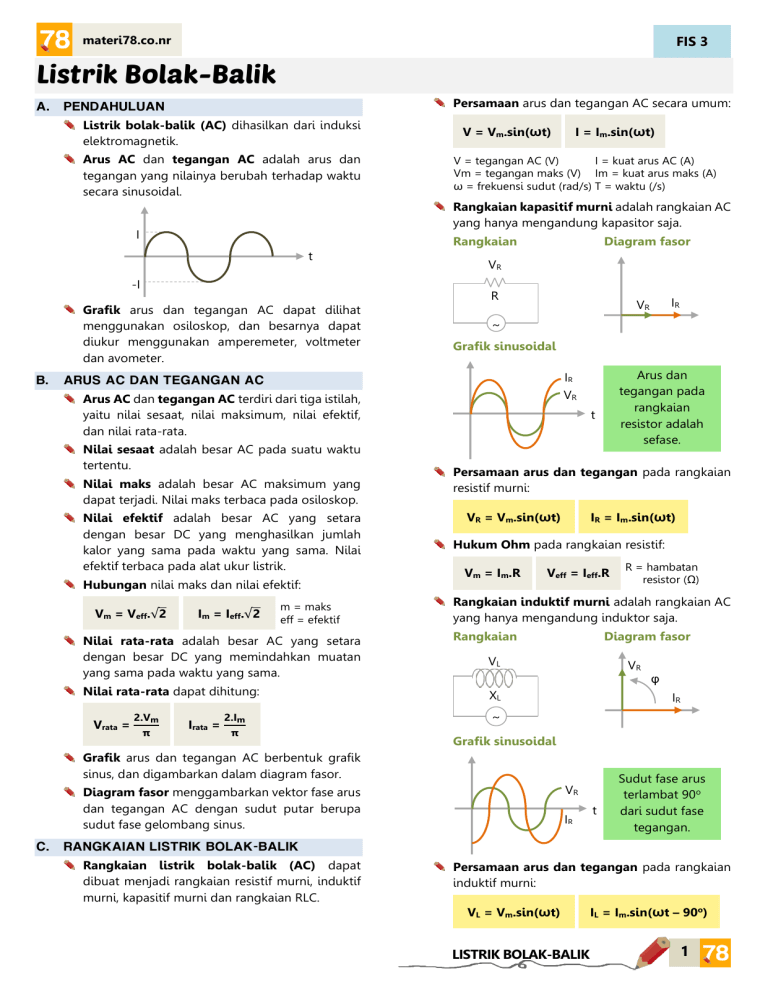
materi78.co.nr
FIS 3
Listrik Bolak-Balik
A.
Persamaan arus dan tegangan AC secara umum:
PENDAHULUAN
Listrik bolak-balik (AC) dihasilkan dari induksi
elektromagnetik.
Arus AC dan tegangan AC adalah arus dan
tegangan yang nilainya berubah terhadap waktu
secara sinusoidal.
V = tegangan AC (V)
I = kuat arus AC (A)
Vm = tegangan maks (V) Im = kuat arus maks (A)
ω = frekuensi sudut (rad/s) T = waktu (/s)
Rangkaian
t
-I
Diagram fasor
VR
R
Grafik arus dan tegangan AC dapat dilihat
menggunakan osiloskop, dan besarnya dapat
diukur menggunakan amperemeter, voltmeter
dan avometer.
~
Grafik sinusoidal
VR
Arus AC dan tegangan AC terdiri dari tiga istilah,
yaitu nilai sesaat, nilai maksimum, nilai efektif,
dan nilai rata-rata.
Nilai maks adalah besar AC maksimum yang
dapat terjadi. Nilai maks terbaca pada osiloskop.
Nilai efektif adalah besar AC yang setara
dengan besar DC yang menghasilkan jumlah
kalor yang sama pada waktu yang sama. Nilai
efektif terbaca pada alat ukur listrik.
Hubungan nilai maks dan nilai efektif:
Vm = Veff.√2
Im = Ieff.√2
m = maks
eff = efektif
Nilai rata-rata adalah besar AC yang setara
dengan besar DC yang memindahkan muatan
yang sama pada waktu yang sama.
Nilai rata-rata dapat dihitung:
2.Vm
π
Irata =
2.Im
π
t
Persamaan arus dan tegangan pada rangkaian
resistif murni:
VR = Vm.sin(ωt)
IR = Im.sin(ωt)
Hukum Ohm pada rangkaian resistif:
Vm = Im.R
Veff = Ieff.R
R = hambatan
resistor (Ω)
Rangkaian induktif murni adalah rangkaian AC
yang hanya mengandung induktor saja.
Rangkaian
Diagram fasor
VL
VR
φ
XL
IR
~
Grafik sinusoidal
Grafik arus dan tegangan AC berbentuk grafik
sinus, dan digambarkan dalam diagram fasor.
VR
Diagram fasor menggambarkan vektor fase arus
dan tegangan AC dengan sudut putar berupa
sudut fase gelombang sinus.
C.
Arus dan
tegangan pada
rangkaian
resistor adalah
sefase.
IR
Nilai sesaat adalah besar AC pada suatu waktu
tertentu.
IR
VR
ARUS AC DAN TEGANGAN AC
Vrata =
I = Im.sin(ωt)
Rangkaian kapasitif murni adalah rangkaian AC
yang hanya mengandung kapasitor saja.
I
B.
V = Vm.sin(ωt)
IR
t
Sudut fase arus
terlambat 90o
dari sudut fase
tegangan.
RANGKAIAN LISTRIK BOLAK-BALIK
Rangkaian listrik bolak-balik (AC) dapat
dibuat menjadi rangkaian resistif murni, induktif
murni, kapasitif murni dan rangkaian RLC.
Persamaan arus dan tegangan pada rangkaian
induktif murni:
VL = Vm.sin(ωt)
LISTRIK BOLAK-BALIK
IL = Im.sin(ωt – 90o)
1
materi78.co.nr
FIS 3
Reaktansi induktif adalah nilai hambatan yang
terdapat pada induktor, dapat dirumuskan:
V = √VR 2 +(VL -VC )2
XL = ω.L = 2πf.L
Impedansi total (Z) adalah hambatan gabungan
total rangkaian RLC.
XL = reaktansi induktif (Ω)
ω = frekuensi sudut (rad/s)
f = frekuensi (Hz)
L = induktansi diri (H)
Z = √R2 +(XL -XC )2
Hukum Ohm pada rangkaian induktif:
Vm = Im.XL
XL = reaktansi
induktif (Ω)
Veff = Ieff.XL
Rangkaian kapasitif murni adalah rangkaian AC
yang hanya mengandung kapasitor saja.
Rangkaian
Diagram fasor
VC
IR
φ
XC
VR
~
t
IR
Sudut fase arus
mendahului 90o
dari sudut fase
tegangan.
Persamaan arus dan tegangan pada rangkaian
kapasitif murni:
VC = Vm.sin(ωt)
IC = Im.sin(ωt + 90o)
Reaktansi kapasitif adalah nilai hambatan yang
terdapat pada kapasitor, dapat dirumuskan:
ω.C
=
2πf.C
XL
~
VR
R
=
VL
XL
=
VC
XC
Beda sudut fase yang terjadi antara kuat arus
listrik (I) dengan tegangan total (V) dapat
dihitung:
VL -VC
VR
=
XL -XC
R
 Fase arus terlambat dari fase tegangan
sebesar 0o ≤ φ ≤ 90o.
 Nilai XL > XC.
2) Kapasitif
 Fase arus medahului fase tegangan
sebesar 0o ≤ φ ≤ 90o.
 Nilai XC > XL.
3) Resistif (resonansi)
Frekuensi sudut yang dihasilkan rangkaian
RLC yang bersifat resistif:
XC = reaktansi
kapasitif (Ω)
Diagram fasor
VR
1) Induktif
V
R
Veff = Ieff.XC
Rangkaian
XC
=
maksimum (I = ).
Rangkaian RLC adalah rangkaian AC yang
mengandung resistor, induktor dan kapasitor seri.
VL
Z
Impedansi total rangkaian bernilai minimum
(Z = R), sedangkan kuat arus listrik bernilai
Hukum Ohm pada rangkaian kapasitif.
VC
V
 Arus dan tegangan adalah sefase.
 Nilai XL = XC.
1
XC = reaktansi kapasitif (Ω)
ω = frekuensi sudut (rad/s)
f = frekuensi (Hz)
C = kapasitansi (F)
Vm = Im.XC
I=
Sifat-sifat rangkaian RLC:
VR
XC =
Kuat arus listrik yang mengalir pada rangkaian
dapat dirumuskan:
tanφ =
Grafik sinusoidal
1
Tegangan total (V) adalah tegangan gabung
total rangkain RLC.
VL
R
ω=
VR
√LC
Frekuensi resonansi yang dihasilkan
rangkaian RLC yang bersifat resistif:
f=
φ
1
1
2π√LC
I
VC
LISTRIK BOLAK-BALIK
2
materi78.co.nr
D.
FIS 3
DAYA RANGKAIAN LISTRIK BOLAK -BALIK
Daya pada rangkaian AC terjadi pada rangkaian
resistif. Pada rangkaian induktif dan kapasitif,
daya rata-rata adalah nol.
Daya rangkaian AC dapat dihitung:
Hubungan dengan tegangan
P = Veff.Ieff.cosφ
Hubungan dengan impedansi
P = Ieff2.Z.cosφ
P = Ieff2.R
dengan nilai cosφ,
cosφ =
R
Z
=
VR
V
LISTRIK BOLAK-BALIK
3