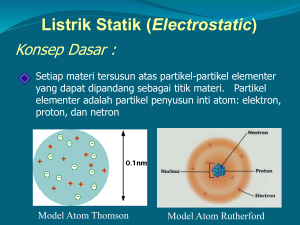
Energi dalam medan listrik

Matakuliah
Tahun
Versi
: K0272/Fisika Dasar III
: 2007
: 0/2
Pertemuan 05-06
Potensial dan Energi Medan
1
Learning Outcomes
Pada akhir pertemuan ini, diharapkan mahasiswa
akan mampu :
• Memberikan definisi dinamika partikel : Hukum
Newton 1 dan 3 , kesetimbangan gaya(partikel) ,
gaya gesek , kesetimbangan momen gaya,
pusat massa(berat) , hukum Newton 2 , gerak
melingkar dan hukum Newton tentang gravitasi
→ C1 (TIK - 1)
2
Outline Materi
• Materi 1
Potensial
- Definisi Potensial
- Potensial oleh banyak muatan
• Materi 2
Tenaga Potensial Listrik
• Materi 3
Energi dalam Medan Listrk
• Materi 4
Gradien
• Materi 5
Hubungan antara V dan E
• Materi 6
Dipol
3
ISI
• Materi yang dibahas dalam pertemuan ini akan
meliputi definisi potensial , potensial disekitar
muatan titik dan muatan kontinu , energi
potensial , energi medan listrik , gradien
potensial dan hubungan antara kuat medan
dengan potensial , dwikutub serta contoh-contoh
soal . .
• Aplikasi dari potensial dan energi di antaranya
terdapat dalam kapasitor , pembangkit tenaga
listrik , sistem pemancar gelombang elektromag
-netik seperti pemancar radar , electrostatic
precipitator (peralatan pembersih udara pada
pabrik semen dan pembangkit listrik tenaga uap
; batu bara) , electro- coating (pelapisan logam)
, peralatan fotocopy dan lain-lain
4
1. POTENSIAL [VOLT = J/C]
- Definisi potensial listrik :
Beda potensial listrik antara dua titik A dan B
yang berada dalam suatu medan listrik adalah
usaha (=WAB ) untuk memindahkan muatan uji
.
q0 dari titik B ke titik A per satuan muatan uji q0
VAB = VA - VB =
.
..
..
….. (01)
Kalau suatu muatan uji q0 akan dipindahkan sejauh dl dalam medan listrik E ,maka q0 akan mengalami gaya sebesar q0E . Agar muatan uji
tidak mengalami percepatan maka harus ada
gaya luar yang besarnya sama dengan – q0E ,
dan usaha gaya ini dalam membawa muatan uji
5
dari A ke B adalah :
dW = - q0E • dl → WAB = - q0 AB E • dl .....(02)
EA
E
EB
•A
•B
- q0E
●q
Dari persamaan (01) diperoleh :
VAB = VA - VB = - ∫AB E • dl
……(03)
Karena medan listrik merupakan medan konservatif maka usaha hanya tergantung dari titik awal
dan akhir lintasan.
6
- Potensial di sebuah titik oleh muatan titik q
Karena kuat medan listrik E bersifat radial
maka dalam mencari potensial dipergunakan
koordinat bola :
Er = k
ar
dl = dr ar
VA = - A E • dl = - rA Er dr
VA = - rA k
= k q 1/r
q
VA = k
rA
dr

rA
; V = 0
…..(04)
7
Selisih potensial antara dua titik A dan B
dimana rA > rB adalah :
VA - VB = kq (1/rA - 1/rB )
- Usaha (Work = W)
Potensial = W/q= usaha persatuan muatan
……(05)
W = qV
- Potensial oleh banyak muatan titik
V = k (q1/r1 + q2/r2 + q3/r3 + .. qN/rN )
n
V = k
qj
j 1 r j
…….(5a)
8
.
- Potensial oleh distribusi muatan kontinu q
pada permukaan bola .
q
r
P
Bola
berjejari
r
dan
P
b
 O
bermuatan q serta
rb
berjarak rP dari titik P
Untuk titik-titik dalam bola , kuat medan listriknya adalah nol sedang untuk titik-titik diluar
bola adalah :rb
Vrb =
dr
- k {(  q 2
r

VrP = k
) + 0} → Vrb = k
q
, r ≥ rb
rP
q
, r ≤ rb
rb
......(06)
9
Grafik potensial sebagai fungsi jejari :
rb
V = kq/rb
r
- Potensial oleh bola konsentrik,bola dalam
jejari rd (A) bermuatan positif dan bola
luar jejari rl (B) bermuatan negatif .
 1 1
q
=  k  2 dr  kq  
r
 rd rl 
rl
rd
VBA
10
Potensial pada jarak r (antara rd dan rl ) yaitu
di titik P:
A dr
VPA = VA - VP =  kq 
r
r
2
 1 1
VPA  kq    →
 rA r 
1 1 
  
r rA 
. ............(07)

VP  VA 
VBA
1 1
  
 rA rB 
11
- Potensial oleh silinder bermuatan
panjang L jejari R di titik P yang berjarak
rP > R .
L
R
L >> R → silinder →∞
rP •P
sehingga seluruh
muatan seakan akan
terdistribusi merata sepanjang sb silinder
Kuat medan listrik dalam silinder adalah nol dan
kuat medan listrik diluar silinder dengan anggapan seluruh muatan terpusat pada sumbu silinder adalah :
12

Er 
2 0 r



ln r]R
VR   
dr 
20 r
2 0

R
Supaya punya arti maka diambil permukaan
silinder potensialnya nol. →

VP 
ln
20
.
.
R
rP
......(08)
- Potensial disekitar bidang tak berhingga
yang bermuatan serba sama σ C/m2 .
Dengan teorema Gauss kuat medan disekitar
13
.
.
sebuah bidang dengan luas tak berhingga
(bidang XY) yang bermuatan σ adalah
.
E = σ/(2ε0 ) i
Kalau potensial di x = o adalah Vo , maka
potensial di x = x menurut persamaan (03) :
Vx – V0 = - 0x E • dl = - 0x σ/(2ε0 )I • idl →
.
.
Vx = V0 – (q/2ε0 ) x , x > 0
.............(9a)
Vx = V0 – (q/2ε0 ) x , x > 0
.............(9b)
- Potensial disekitar garis tak berhingga
yang bermuatan serba sama λ C/m
Dengan teorema Gauss kuat medan disekitar
sebuah garis dengan panjang tak berhingga
14
.
yang bermuatan λ C/m adalah :
Er = 2 k λ / r
→
menurut persamaan (03) :
dV = - E • dl = - (2kλ/r) dr
V = - 0r (2kλ/r) dr = V0 – 2kλ ln r .........(10a)
Untuk pertambahan r >> maka V << → r = 
.
potensial V tak dapat dipilih nol , demikian pula
.
untuk r = 0 , Vr=0 .tak dapat dipilih 0 karen ln r
.
mendekati tak berhingga untuk r mendekati nol ,
.
sehingga dipilih Vr=a = 0 , sehingga persamaan .
(9a) menjadi :
0 = V0 – 2kλ ln a atau V0 = 2kλ ln a →
V = 2k λ ln (r/a)
..............(10b)
15
2. Tenaga potensial listrik(U)
Potensial = usaha persatuan muatan = W/q
→
W = qV
Tinjau dua muatan q1 dan q2 :
q1 ●
●q2
r12
Seandainya q2 dikembalikan ke tak terhingga
sehingga tempat tersebut menjadi kosong ma
ka potensial di titik tersebut adalah:
V21 = k q1 /r12
Kalau muatan q2 ditempatkan dari tak terhingga ke tempat semula maka usahanya
16
adalah:
U (=W) = k q1 q2 /r12 = q2 V21 ......(11a)
Kalau terdapat tiga muatan q1 ,q2 dan q3
dalam kedudukan tetap maka usaha untuk
menempatkan ketiga muatan tersebut pada
kedudukannya adalah :
U = 0 + q2 V21 + q3 V31 + q3 V32
atau U = 0 + q2V23 + q1 V13 + q1 V12
2U = 0 + q1 (V13 + V12 ) + q2 (V23 + V21 ) + ….
q3 (V31 + V32 ) → V 1 = V12 + V13
U = ½ {q1 V1 + q2 V2 + q3 V3
17
Tenaga potensial dari N buah system muatan
adalah :
...
U = U12 + U13 + U23 + …atau
U = ½∑j=1j=N qj Vj ; Vj = V j2+ Vj3 + ..VjN ....(11b)
Contoh soal : Berapakah tenaga yang tersim –
pan dalam sistem dua muatan q1 = 3nC dan
q2 = -3nCbila jarak antara ke duanya 0.2 cm .
Jawaban :
2 WE = q1 V1 + q2 V2 = (1/4πε0d)(q1q2 + q2q1)
9 2
(3 x 10 )
WE = q1q2/4πε0d = 
  405 J
9
4 (10 / 36  )0.2
Jelaskan mengapa nilainya negatif
18
3. Energi dalam medan listrik
W = ½ ∑ qn Vn
atau W = ½ ∫ D•E dv
Untuk kapasitor : W = ½ q V2
…..(12)
4. Gradien
Dalam suatu ruang terdapat fungsi scalar
V dan titik P dan K merupakan dua titik yang
berdekatan.
z
Z
V(x,y,z)*
P dr
d
r
r+dr
V(x,y,z)
Y
Y
X
X
19
dr = dx i + dy j + dz k
Perubahan potensial V dari titik P ke K adalah :
dV = ∂V/∂x dx + ∂V/∂y dy +∂V/∂z dz
Operator  = Del :
 = i ∂ ( )/ ∂x + j ∂ ( )/ ∂y + k ∂ ( )/ ∂z
▽V = grad V = i ∂V/∂x + j ∂V/∂y + k ∂V/∂z
dV = ▽V • dr
Gradien suatu fungsi potensial senantiasa
tegak lurus bidang ekipotensial
Gradien dalam system koordinat:
V 
V
V
V
ar 
a  k (silinder )
r
r
z
20
V
V
V
V 
ar 
a 
a (bola)
r
r  r sin
5. Hubungan antara E dan V :
dV = ▽V • dr
V = -  E  dr → dV = - E • dr
→ E=- V
……(13)
6. Dipol
Dipol adalah sepasang muatan listrik yang
berlawanan tanda dan yang jarak antara
keduanya sangat kecil dibandingkan dengan
jarak pengamatan medan listrik pasangan
tersebut .
21
z
+q •
d
R1
r
P
y
R2
-q •
Potensial oleh muatan +q dan -q di titik P
adalah :
VP = kq (1/R2 - 1/ R1) = kq (R2 – R) /(R1R2)
…….(14)
Bila titik P jauh maka :
R1 = R2 → R1R2 = r2 dan
R2 - R1 = d cos θ →
22
qd = p = momen dwikutub
Sehingga persamaan (11) , menjadi :
VP = k p (cos θ / r2 ) dan
E = -V
Dengan koordinat bola diperoleh
E = kp/r3 (2cos θ ar + sin θ aθ ) ...(14a)
Contoh 1: Diketahui fungsi potensial dalam
vakum V = (2x + 4y) volt.Tetapkan energi
yang tersimpan dalam volum 1m3 yang
berpusat di titik asal
Jawaban :
E = -V = ∂V/∂x i + ∂V/∂y j +∂V/∂z k
= -2i – 4j volt
23
(Ternyata harga medan besar dan arahnya
konstan diseluruh ruang , E= √20 volt).
Besar energi yang tersimpan adalah :
W = ½ ∫D•E dv = ½ ε0 E2 ∫dv→
w = kerapatan energi persatuan volum
w = ½ ε0 E2 = ½ x 10-9/36π x 20 J/m3
w = 10-8 /36π J/m3 →
untuk setiap 1 m terdapat : 10-8 /36π J
Contoh 2 : Lima muatan titik yang sama besar
35 nC berada masing-masing di x = ±3m ,
y = ± 3m dan di z = -3m .
a).Berapakah potensial di titik P(0,0,4)m.
b).Berapa energi system muatan tersebut?
24
a). V = = 9 x 109 Nm2 /C2 x 35 x 10-9 C x
{4(1/5m) + 1/7m} = 432 Nm/C = 432 J/C
V = 432 volt
b).W = ½ ∑ qn Vn
V1 = V2 = V3 = V4 = 9 x 109 x 35 x 10-9 x 1/5
= 49 v , V5 = 45 v
= ½ {4 x 35 x 10-9 x 49 + 35 x 10-9 x 45}J
W = 4.218 μJ
25
animasi / simulasi
http://www.cco.caltech.edu/~phys1/java/phys1/
MovingCharge/MovingCharge.html
http://www3.ltu.edu/~s_schneider/physlets/main/erings.shtml
26
Rangkuman :
1. Beda potensial didefinisikan sebagai usaha
. negatif persatuan muatan uji yang dikerjakan
. oleh medan saat muatan uji bergerak dari titik A
. ke titik B .
 V = VB – VA = - AB E . dl
.
.
.
.
.
- potensial di tak terhingga adalah nol , V = 0
- satuan potensial adalah volt (V) :
1V = 1J/C
- satuan medan listrik adalah :
1N/C = 1V/m
2. Potensial di titik P yang berjarak r dari muatan
27
.
titik q adalah :
- potensial untuk sistem muatan titik :
3. Potensial dari muatan terdistribusi merata adalah :
4. Energi potensial sistem muatan titik adalah usaha
.
untuk menempatkan muatan-muatan tersebut
.
pada tempatnya
5. Tenaga potensial dari N buah system muatan
titik adalah : ...
28
jN
U  1 2  q jV j ; V j  V j 2  V j 3  ...V jN
j 1
6. Gradien () adalah suatu operator matematik :



i
 j
 k
x
y
z
- gradien , , suatu potensial , V adalah :
▽V
7. Hubungan kuat medan listrik E fengan V
E = - grad V = - V
8. Potensial oleh sebuah dwikutub
VP = k p (cos θ / r2 )
29
<< CLOSING>>
Setelah menyelesaikan dengan baik mata kuliah ini dan
materi–materi sebelumnya mahasiswa diharapkan sudah
mampu membuat dan menyelesaikan masalah-masalah
yang berhubung an dengan energi dan potensial listrik
khususnya yang terkait dengan bidang sistem komputer
30
31