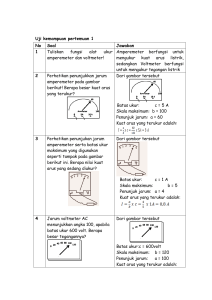
BAB IV METODA ANALISIS RANGKAIAN Metoda analisis rangkaian
advertisement

60 Rangkaian Listrik BAB IV METODA ANALISIS RANGKAIAN Metoda analisis rangkaian sebenarnya merupakan salah satu alat bantu untuk menyelesaikan suatu permasalahan yang muncul dalam menganalisis suatu rangkaian, bilamana konsep dasar atau hukum-hukum dasar seperti Hukum Ohm dan Hukum Kirchoff tidak dapat menyelesaikan permasalahan pada rangkaian tersebut. Pada bab ini akan dibahas tiga metoda analisis rangkaian yang akan dipakai, yaitu : analisis node, analisis mesh dan analisis arus cabang. Analisis Node Sebelum membahas metoda ini ada beberapa hal yang perlu diperhatikan yaitu pengertian mengenai tentang node. Node atau titik simpul adalah titik pertemuan dari dua atau lebih elemen rangkaian. Junction atau titik simpul utama atau titik percabangan adalah titik pertemuan dari tiga atau lebih elemen rangkaian. Untuk lebih jelasnya mengenai dua pengertian dasar diatas, dapat dimodelkan dengan contoh gambar berikut. Contoh : Jumlah node Jumlah junction = 5, yaitu : a, b, c, d, e=f=g=h = 3, yaitu : b, c, e=f=g=h Analisis node berprinsip pada Hukum Kirchoff I/ KCL dimana jumlah arus yang masuk dan keluar dari titik percabangan akan samadengan nol, dimana tegangan merupakan parameter yang tidak diketahui. Atau analisis node lebih mudah jika pencatunya semuanya adalah sumber arus. Analisis ini dapat diterapkan pada sumber searah/ DC maupun sumber bolak-balik/ AC. Beberapa hal yang perlu diperhatikan pada analisis node, yaitu : Tentukan node referensi sebagai ground/ potensial nol. Tentukan node voltage, yaitu tegangan antara node non referensi dan ground. Asumsikan tegangan node yang sedang diperhitungkan lebih tinggi daripada tegangan node manapun, sehingga arah arus keluar dari node tersebut positif. Jika terdapat N node, maka jumlah node voltage adalah (N-1). Jumlah node voltage ini akan menentukan banyaknya persamaan yang dihasilkan. Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 61 Rangkaian Listrik Contoh latihan : 1. Tentukan nilai i dengan analisis node ! Jawaban : - Tentukan node referensinya/ground - Tentukan node voltage - Jumlah N=3, jumlah persamaan (N - 1) = 2 Tinjau node voltage V1 : KCL : ∑ i = 0 → 4 − 7 − i1 − i2 = 0 i1 + i2 = −3 V1 − V g V1 − V2 = −3 → V g = 0 4 8 V1 − 0 V1 − V2 + = −3 4 8 2V1 + V1 − V2 = −24 + 3V1 − V2 = −24 KK (1) Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 62 Rangkaian Listrik Tinjau node voltage V2 : KCL : ∑ i = 0 → 7 − i1 − i2 = 0 i1 + i2 = 7 V2 − V1 V2 − V g + = 7 → Vg = 0 8 12 V2 − V1 V2 − 0 + =7 8 12 3(V2 − V1 ) + 2V2 = 168 5V2 − 3V1 = 168KK (2) Dari kedua persamaan diatas, dapat diselesaikan dengan 2 cara, yaitu : 1. Cara substitusi 3V1 − V2 = −24 − 3V1 + 5V2 = 168 + 4V2 = 144 → V2 = 36 ⋅ volt V2 dapat dimasukkan kesalah satu persamaan, misalkan persamaan (1) : 3V1 − V2 = −24 3V1 − 36 = −24 3V1 = 36 − 24 = 12 → V1 = 4 ⋅ volt V1 − V g 4−0 = 1⋅ A 4 4 2. Cara Metoda Cramer Menggunakan matrik : i= = 3V1 − V2 = −24 − 3V1 + 5V2 = 168 Matrik : 3 − 1 V1 − 24 = − 3 5 V2 168 Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 63 Rangkaian Listrik ∆= 3 −1 −3 5 = 3.5 − (−1).(−3) = 12 sehingga ; V1 = V2 = i= − 24 − 1 168 5 ∆ = − 24.5 − (−1).168 = 4 ⋅ volt 12 = 3.168 − (−24).(−3) = 36 ⋅ volt 12 3 − 24 − 3 168 ∆ V1 − V g 4 = 1⋅ A 2. Tentukan nilai tegangan v dengan analisis node ! Jawaban : - Tentukan node referensinya/ground - Tentukan node voltage Tinjau node voltage va : Σi = 0 v a − vb v a − 0 + −9 = 0 16 8 v a − vb v a + =9 16 8 3v a − vb = 144........(1) Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 64 Rangkaian Listrik Tinjau node voltage vb : Σi = 0 vb − v a vb − 0 + −3 = 0 16 12 vb − v a vb + =3 16 12 − 3v a + 7vb = 144........(2) Substitusikan pers. (1) dan (2) : 3v a − vb = 144 − 3v a + 7vb = 144 + 288 = 48V 6 Masukan nilai vb ke persamaan (1) : 3v a − vb = 144 6vb = 288 → vb = 3v a − 48 = 144 3v a = 144 + 48 = 192 va = 192 = 64V 3 3. Tentukan nilai arus i dengan analisis node! Jawaban : - Tentukan node referensinya/ground - Tentukan node voltage Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 65 Rangkaian Listrik Tinjau node voltage va : v a − vb v a + + 12 − 6i = 0 40 10 v dim ana : i = a 10 v a − vb v a 6v + + 12 − a = 0 40 10 10 19v a + vb = 480.......(1) Tinjau node voltage vb : vb − v a vb + + 6i − 2 = 0 40 20 vb − v a vb 6v a + + −2=0 40 20 10 23v a + 3vb = 80.......(2) Metoda Cramer : 19 1 v a 480 = 23 3 vb 80 480 80 va = 19 23 1 3 480.3 − 80.1 = = 40V 1 19.3 − 23.1 3 sehingga : v 40 = 4A i= a = 10 10 Analisis node mudah dilakukan bila pencatunya berupa sumber arus. Apabila pada rangkaian tersebut terdapat sumber tegangan, maka sumber tegangan tersebut diperlakukan sebagai supernode, yaitu menganggap sumber tegangan tersebut dianggap sebagai satu node. Contoh latihan : 1. Tentukan nilai i dengan analisis node ! Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 66 Rangkaian Listrik Jawaban : - Tentukan node referensinya/ground - Tentukan node voltage - Teg. Sumber sebagai supernode - Jumlah N=3, jumlah persamaan (N-1)=2 Tinjau node voltage di V : KCL : ∑i = 0 V − 20 V − Vg + − 1 = 0 → Vg = 0 10 10 V − 20 V + =1 10 10 2V − 20 = 10 → V = 15 ⋅ volt KK (1) 20 − V KK (2) 10 20 − 15 i= = 0,5 ⋅ A 10 i= 2. Tentukan nilai tegangan v dengan analisis node ! Jawaban : - Tentukan node referensinya/ground - Tentukan node voltage - Teg. Sumber sebagai supernode Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 67 Rangkaian Listrik Tinjau node voltage va : v a − 16 v a + −3 = 0 8 12 3v a − 48 + 2v a − 72 = 0 5v a − 120 = 0 120 = 24V 5 v = v a − 16 = 24 − 16 = 8V va = 3. Tentukan nilai arus i dengan analisis node! Jawaban : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 68 Rangkaian Listrik Tinjau node voltage va : v a − 14 v a v a + 4 v a + 4 + + + =0 4 2 12 4 3v a − 42 + 6v a + v a + 4 + 3v a + 12 = 0 13v a − 26 = 0 va = 26 = 2V 13 sehingga : i = va 2 = = 1A 2 2 Analisis Mesh atau Arus Loop Arus loop adalah arus yang dimisalkan mengalir dalam suatu loop (lintasan tertutup). Arus loop sebenarnya tidak dapat diukur (arus permisalan). Berbeda dengan analisis node, pada analisis ini berprinsip pada Hukum Kirchoff II/ KVL dimana jumlah tegangan pada satu lintasan tertutup samadengan nol atau arus merupakan parameter yang tidak diketahui. Analisis ini dapat diterapkan pada rangkaian sumber searah/ DC maupun sumber bolak-balik/ AC. Hal-hal yang perlu diperhatikan : Buatlah pada setiap loop arus asumsi yang melingkari loop. Pengambilan arus loop terserah kita yang terpenting masih dalam satu lintasan tertutup. Arah arus dapat searah satu sama lain ataupun berlawanan baik searah jarum jam maupun berlawanan dengan arah jarum jam. Biasanya jumlah arus loop menunjukkan jumlah persamaan arus yang terjadi. Metoda ini mudah jika sumber pencatunya adalah sumber tegangan. Jumlah persamaan = Jumlah cabang – Jumlah junction + 1 Contoh latihan : 1. Tentukan nilai arus i dengan analisis mesh! Jawaban : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 69 Rangkaian Listrik Tinjau loop I1 : Σv = 0 − 16 + 2 I 1 + 9 + 3( I 1 − I 2 ) = 0 5I 1 − 3I 2 = 7........(1) Tinjau loop I2 : Σv = 0 − 9 + 6 + 6 I 2 + 3( I 2 − I 1 ) = 0 − 3I 1 + 9 I 2 = 3........(2) Substitusikan persamaan (1) dan (2) : 5I 1 − 3I 2 = 7..........x3 − 3I 1 + 9 I 2 = 3........x1 + 12 I 1 = 24 24 = 2A 12 sehingga : i = I 1 = 2 A I1 = 2. Tentukan nilai tegangan v dengan analisis mesh! Jawaban : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 70 Rangkaian Listrik Tinjau loop I1: − 18 + 5 I 1 + 12( I 1 − I 2 ) = 0 17 I 1 − 12 I 2 = 18..........(1) Tinjau loop I2: 20 I 2 + 40 I 2 + 12( I 2 − I 1 ) = 0 − 12 I 1 + 72 I 2 = 0..........(2) substitusikan persamaan (1) dan (2) : 72 I2 − 12 I 1 + 72 I 2 = 0 → I 1 = 12 17 I 1 − 12 I 2 = 18 102 I 2 − 12 I 2 = 18 → 90 I 2 = 18 I2 = 18 2 = A 90 10 sehingga : v = I 2 x 40Ω = 2 x 40 = 8V 10 3. Tentukan nilai i dengan analisis mesh! Jawaban : Tinjau loop I1 : Σv = 0 − 5 + 6 I 1 − 5ia = 0 dim ana : I 1 = ia − 5 + 6ia − 5ia = 0 → ia = 5 A Tinjau loop I2 : Σv = 0 + 5ia + 10 I 2 + 25 = 0 25 + 10 I 2 + 25 = 0 → I 2 = − 50 = −5 A 10 i = − I 2 = −(−5) = 5 A Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 71 Rangkaian Listrik Apabila ada sumber arus, maka diperlakukan sebagai supermesh. Pada supermesh, pemilihan lintasan menghindari sumber arus karena pada sumber arus tidak diketahui besar tegangan terminalnya. Contoh latihan : 1. Tentukan nilai i dengan analisis mesh ! Jawaban : Tinjau loop I1 : I1 = 9 A Tinjau loop I2 dan I3 : I 3 − I 2 = 3A I 3 = 3 + I 2 .......................................(1) Tinjau lintasan supermesh : Σv = 0 8( I 2 − I 1 ) + 16 I 2 + 12 I 3 = 0..............(2) substitusikan persamaan (1) dan (2) : 8( I 2 − 9) + 16 I 2 + 12(3 + I 2 ) = 0 8 I 2 − 72 + 16 I 2 + 36 + 12 I 2 = 0 36 = 1A 36 sehingga : i = I 2 = 1A 36 I 2 = 36 → I 2 = Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 72 Rangkaian Listrik 2. Tentukan nilai V dengan analisis mesh ! Jawaban : Tinjau loop I1 dan I2 : I 2 − I1 = 6 A I 1 = I 2 − 6.................................(1) dim ana : i = I 1 Tinjau lintasan supermesh : Σv = 0 − 12 + 1.I 1 + 2i + 3I 2 = 0 − 12 + I 1 + 2 I 1 + 3I 2 = 0 3I 1 + 3I 2 = 12............................(2) Substitusikan persamaan (1) dan (2) : 3( I 2 − 6) + 3I 2 = 12 3I 2 − 18 + 3I 2 = 12 30 = 5A 6 sehingga : V = 3I 2 = 3 x5 = 15V 6 I 2 = 30 → I 2 = Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 73 Rangkaian Listrik 3. Tentukan nilai arus i dengan analisis mesh ! Jawaban : Tinjau loop I1 : 6 I 1 + 12 + 12( I 1 − I 2 ) = 0 18 I 1 − 12 I 2 = −12.............................(1) Tinjau loop I2 dan I3 : I 3 − I 2 = 3.........................................(2) Tinjau lintasan supermesh : Σv = 0 4 I 2 + 6 I 3 + 12( I 2 − I 1 ) − 12 = 0 16 I 2 − 12 I 1 + 6 I 3 = 12........................(3) Metoda Cramer : 18 − 12 0 I 1 − 12 − 1 1 I 2 = 3 0 − 12 16 6 I 12 3 18 − 12 − 12 I3 = 0 − 12 −1 16 3 12 18 − 12 0 0 −1 1 − 12 16 6 18 = 0 3 0 −1 3 −1 + 12 − 12 16 12 − 12 12 − 12 16 = 2A 0 1 −1 1 18 + 12 16 6 − 12 6 sehingga : i = I 3 − 2 A Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 74 Rangkaian Listrik Analisis Arus Cabang Arus cabang adalah arus yang benar-benar ada (dapat diukur) yang mengalir pada suatu cabang. Artinya arus cabang adalah arus yang sebenarnya mengalir pada percabangan tersebut. Arti cabang : Mempunyai satu elemen rangkaian Bagian rangkaian dengan dua terminal dengan arus yang sama Jumlah persamaan = Jumlah arus cabang yang ada Contoh latihan : 1. Tentukan semua persamaan yang ada ! Jawaban : Σ persamaan = Σ arus cabang = 3 Tinjau arus cabang i1 dan i2 : ΣV = 0 i1 R1 + i 2 R2 − V = 0 KK (1) Tinjau arus cabang i3 : i3 = I K.....................K (2) Tinjau arus cabang i2 : Σi = 0 i1 + i3 = i2 ........................(3) 2. Tentukan nilai i dengan analisis arus cabang ! Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 75 Rangkaian Listrik Jawaban : Tinjau arus cabang i1 dan i2 : i1 + i2 + 7 = 4 i1 + i2 = −3...............(1) Tinjau arus cabang i2 dan i3 : i 2 + 7 = i3 i2 − i3 = −7...............(2) Tinjau lintasan tertutup semua arus cabang Σv = 0 8i2 + 12i3 − 4i1 = 0..........(3) Metoda Cramer : 1 1 0 i1 − 3 0 1 − 1 i 2 = − 7 − 4 8 12 i 0 3 −3 1 0 − 7 1 −1 0 8 12 1 −1 − 7 −1 8 12 0 i1 = = 1 1 0 1 −1 0 1 −1 0 1 −1 8 12 −4 − 4 8 12 −3 −1 −7 +0 12 0 0 −1 +0 12 −4 1 8 24 = = 1A 1 24 8 sehingga : i = i1 = 1A Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 76 Rangkaian Listrik Soal – soal : 1. Tentukan arus i dengan analisis node ! 2. Tentukan tegangan v dengan analisis node ! 3. Tentukan tegangan v dengan analisis node ! 4. Tentukan i dengan analisis mesh ! Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 77 Rangkaian Listrik 5. Tentukan i dengan analisis mesh ! 6. Tentukan i dengan analisis node ! 7. Tentukan nilai ia dengan analisis node ! 8. Tentukan Vab dengan analisis mesh ! Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 78 Rangkaian Listrik 9. Tentukan tegangan V dengan metoda node : 10. Tentukan arus i dengan metoda node : 11. Tentukan arus i pada rangkaian berikut dengan metoda node : 12. Tentukan arus i dengan metoda node pada rangkaian berikut : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 79 Rangkaian Listrik 13. Tentukan arus i dengan metoda node pada rangkaian berikut : 14. Tentukan tegangan V dengan metoda node pada rangkaian berikut : 15. Tentukan arus i dengan metoda node (supernode) pada rangkaian berikut : 16. Tentukan arus i dengan metoda node (supernode) pada rangkaian berikut : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 80 Rangkaian Listrik 17. Tentukan tegangan V dengan metoda node (supernode) pada rangkaian berikut : 18. Tentukan tegangan V dengan metoda node (supernode) pada rangkaian berikut : 19. Tentukan tegangan V dengan metoda node (supernode) pada rangkaian berikut : 20. Tentukan arus pada R = 2Ω : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 81 Rangkaian Listrik 21. Tentukan V : 22. Tentukan daya yang diserap oleh sumber arus 1 mA : 23. Tentukan nilai tegangan V : 24. Tentukan V : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 82 Rangkaian Listrik 25. Tentukan V : 26. Tentukan V : 27. Tentukan V : 28. Tentukan Vx : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 83 Rangkaian Listrik 29. Tentukan V dan i : 30. Tentukan V1 dan i2 : 31. Tentukan ix dan Vx : 32. Tentukan i : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 84 Rangkaian Listrik 33. Tentukan Vx : 34. Tentukan i dengan node : 35. Tentukan i dengan node : 36. Tentukan tegangan V dengan node : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 85 Rangkaian Listrik 37. Tentukan i dengan node : 38. Tentukan tegangan VA dan V : 39. Tentukan arus i1 dengan node : 40. Tentukan tegangan V1 : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 86 Rangkaian Listrik 41. Tentukan i dengan node : 42. Tentukan tegangan V dengan node : 43. Tentukan arus i dengan node : 44. Tentukan arus i dngan node : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 87 Rangkaian Listrik 45. Tentukan arus i dengan node : 46. Tentukan nilai arus i dengan analisis mesh pada rangkaian berikut : 47. Tentukan tegangan V dengan mesh pada rangkaian berikut : 48. Tentukan arus i dengan analisis mesh pada rangkaian berikut : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 88 Rangkaian Listrik 49. Tentujkan tegangan V dengan analisis mesh pada rangkaian berikut : 50. Tentukan arus i denagan analisis mesh pada rangkaian berikut : 51. Tentukan arus i dengan analisis supermesh pada rangkaian berikut : 52. Tentukan tegangan V dengan analisis supermesh pada rangkaian berikut : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 89 Rangkaian Listrik 53. Tentukan tegangan V dengan analisis supermesh pada rangkaian berikut : 54. Tentukan arus i : 55. Tentukan i : 56. Tentukan i : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 90 Rangkaian Listrik 57. Tentukan i : 58. Tentukan i : 59. Tentukana i : 60. Tentukan daya pada R = 2Ω : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom 91 Rangkaian Listrik 61. Tentukan i : Mohamad Ramdhani Sekolah Tinggi Teknologi Telkom