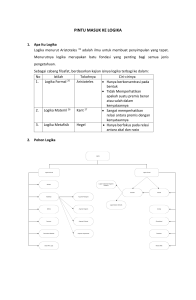
dasar-dasar logika

Logika Informatika
BAB I
DASAR LOGIKA
1.1 Kalimat Deklaratif
Ilmu logika berhubungan dengan kalimat-kalimat (argumen-argumen) dan hubungan
yang ada di antara kalimat-kalimat tersebut. Tujuannya adalah memeberikan aturanaturan sehingga orang dapat menentukan apakah suatu kalimat bernialai benar.
Kalimat yang dipelajari dalam logika bersifat umum, baik bahasa sehari-hari maupun
bukti matematika yang didasarkan atas hipotesa-hipotesa. Oleh karena itu, aturanaturan yang berlaku di dalamnya haruslah bersifat umum dan tidak tergantung pada
kalimat atau disiplin ilmu tertentu.Ilmu logika lebih mengarah pada bentuk kalimat
(sintaks) daripada arti kalimat itu sendiri (semantik)
Suatu Kalimat Deklaratif (Proposisi) adalah kalimat yang bernilai benar atau salah,
tetapi tidak keduanya.
Contoh Proposisi:
a. 2 + 2 = 4
(bernilai benar)
b. 4 adalah bilangan prima
(bernilai salah)
c. Jakarta adalah ibukota negara Indonesia. (bernilai benar)
d. Penduduk Indonesia berjumlah 50 juta.
(bernilai salah)
Contoh Bukan Proposisi :
a. Dimana letak pulau Bali ?
(kalimat tanya)
b. Simon lebih tinggi dari Lina
(ada banyak orang bernama Simon
atau Lina di dunia)
c. x + y = 2
(nilaikebenaran tergantung niali x
dan y)
d. 2 mencintai 3
(relasi mencintai tidak berlaku di
bilangan)
.
STMIK ‘Sinus’ Ska
i
Wawan Laksito YS
Logika Informatika -1
1.2 Penghubung Kalimat
Seringkali beberapa kalimat perlu digabungkan menjadi satu kalimat yang lebih
panjang, sehingga diperlukan penghubung kalimat. Dalam Logika dikenal 5
penghubung :
Simbol
Arti
Bentuk
~
Tidak / Not / Negasi
Tidak …..

Dan / And / konjungsi
…… dan …….

Atau / Or / Disjungsi
…… atau ……

Imlikasi
Jika …. Maka …..

Bi-Implikasi
….. bila dan hanya bila ….
Dalam matematika digunakan huruf-huruf kecil seperti p, q, r,…. Untuk menyatakan
sub kalimat dan simbol-simbol penghubung untuk menyatakan penghubung kalimat.
Contoh :
a. Misal p menyatakan kalimat “ 4 adalah bilangan genap”
q menyatakan kalimat “3 adalah bilangan ganjil”
maka kalimat “ 4 adalah bilangan genap dan 3 adalah bilangan ganjil” dapat
dinyatakan dengan simbol p  q
b. Misal p : 2 + 2 = 4
q : bunga melati berwarna putih.
maka kalimat “Jika 2 + 2 = 4, maka bunga melati berwarna putih” dapat
dinyatakan dengan simbol p  q
Pada contoh b diatas, kalau kalimat tersebut diartikan dalam kehidupan sehari
maka kalimat tersebut tidak berarti (tidak ada hubungan antara kedua kalimat
penyusunnya). Tetapi secara logika matematis hal tersebut dapat diterima, karena
di dalam matematika tidak disyaratkan adanya adanya hubungan antara kedua
kalimat penyusunnya. Dalam Logika matematika, penekanan lebih ditujukan
kepada bentuk/susunan kalimat saja (sintak), dan bukan pada arti kalimat
penyusunnya dalam kehidupan sehari-hari (semantik). Kebenaran suatu kalimat
berimplikasi semata-mata hanya tergantung pada nilai kebenaran kalimat
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -2
penyusunnya, dan tidak tergantung pada ada/tidaknya relasi antara kalimatkalimat penyusunnya.
Jika p dan q merupakan kalimat-kalimat, maka tabel kebenaran penghubung
tampak pada tabel berikut :
p
q
~p
pq
pq
pq
pq
T
T
F
T
T
T
T
T
F
F
F
T
F
F
F
T
T
F
T
T
F
F
F
T
F
F
T
T
( T = True/benar, F = False/salah )
Secara umum, jika ada n variabel (p,q,…), maka tabel kebenaran memuat 2n baris.
Dari tabel :
 p  q bernilai benar jika p maupun q benar, selain itu bernilai salah
 p  q bernilai benar jika ada sedikitnya satu variabel bernilai benar
 Dalam kalimat p  q , p disebut hipotesis (anteseden) dan q disebut konklusi
(konsekuen). Kalimat p  q disebut kalimat berkondisi karena kebenaran kalimat
q tergantung pada kebenaran kalimat p. kalimat p  q akan berniali salah kalau p
benar dan q salah. Sebagai contoh perhatikan apa yang diucapkan seorang pria
terhadap kekasihnya berikut ini :
“Jika besok cerah, maka aku datang” >> p : “besok cerah” , q : “aku akan
datang”
- Jika baik p maupun q keduanya benar (baris ke-1 tabel kebenaran), pria tersebut
tidak berbohong.
- jika p salah (ternyata keesokan harinya hujan, tidak cerah), maka pria tersebut
terbebas dari janjinya karena janji tersebut bersyarat, yaitu kalau besok cerah.
Jadi, baik pria tersebut datang (berarti q benar, sehingga menyatakan baris ke-3
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -3
tabel) maupun tidak datang (q salah ,sehingga menyatakan baris ke-4 tabel), pria
tersebut tidak akan disalahkan.
- Akan tetapi, pria tersebut akan disalahkan (berarti implikasi berniali salah)
apabila keesokkan harinya cuaca cerah ( p benar) tetapi ia tidak datang (q salah).
Ini sesuai baris ke-2 tabel.
 Kalimat kondisi ganda (biconditional) p  q ,berarti (p  q)  (q  p). Supaya
p  q berniali benar maka p  q maupun q  p, keduanya harus bernilai
benar (ingat bahwa kedua implikasi tersebut dihubungkan dengan kata hubung
“dan”). Perhatikan tabel berikut :
p
q
pq
qp
p  q atau (p  q) ( q  p)
T
T
T
T
T
T
F
F
T
F
F
T
T
F
F
F
T
T
T
T
Jadi p  q bernilai benar jika p dan q keduanya bernilai benar atau keduanya
bernilai salah
Soal Latihan :
1. Misal k : Monde orang kaya, s : Monde bersuka cita
Tulislah bentuk simbolis kalimat-kalimat berikut :
a. Monde orang yang miskin tetapi bersuka cita
b. Monde orang kaya atau ia sedih
c. Monde tidak kaya ataupun bersuka cita
d. Monde seorang yang miskin atau ia kaya tetapi sedih.
Anggaplah ingkaran kaya adalah miskin, ingkaran dari bersuka cita adalah
sedih.
2. Buatlah tabel kebenaran untuk kalimat dalam bentuk simbol-simbol logika dibawah
ini !
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -4
a. ~(~p  ~q)
c. (p  q)  ~(p  q)
b. ~(~p  q)
d. (~p  (~q  r))  (q  r)  (p  r)
3. Pada kondisi bagaimanakah agar kalimat di bawah ini bernilai benar ?
“Tidaklah benar kalau rumah kuno selalu bersalju atau angker, dan tidak juga
benar kalau sebuah hotel selalu hangat atau rumah kuno selalu rusak.”
4. Jika p dan q bernilai benar (T) ; r dan s bernilai salah (F)
Tentukan nilai kebenaran kalimat berikut ini :
a. p  (q  r)
b. (p  q  r)  ~((p  q)  ( r  s))
c. (~(p  q)  ~r)  (((~p  q)  ~r)  s)
Dua kalimat disebut Ekuivalen (secara logika) bila dan hanya bila keduannya
mempunyai nilai kebenaran yang sama untuk semua substitusi nilai kebenaran
masing-masing kalimat penyusunnya. Jika p dan q adalah kalimat-kalimat yang
ekuivalen, maka dituliskan p  q .
Soal Latihan
5. Tentukan apakah pasangan kalimat-kalimat di bawah ini ekuivalen
a. ~(~p) dengan p
b. ~(p  q) dengan ~p  ~q
c. p  q dengan ~p  q
Beberapa hukum ekuivalensi logika disajikan dalam daftar dibawah ini :
1. Hukum Komutatif
:pqqp ; pq qp
2. hukum Asosiatif
: (p  q)  r  p  (q  r)
(p  q)  r  p  (q  r)
3. Hukum Distributif
: p  (q  r)  (p  q)  (p  r)
p  (q  r )  (p  q)  (p  r)
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -5
4. Hukum Identitas
: pTp ; pFp
5. Hukum Ikatan
: pTT ; pFF
6. Hukum Negasi
: p  ~p  T ; p  ~p  F
7. Hukum Negasi Ganda : ~(~p)  p
8. Hukum Idempoten
: ppp ; ppp
9. Hukum De Morgan : ~(p  q)  ~p  ~q
~(p  q)  ~p  ~q
10. Hukum Absorbsi
: p  (p  q)  p
11. Negasi T dan F
: ~T  F
Dengan
hukum-hukum
tersebut,
; p  (p  q)  p
; ~F  T
kalimat-kalimat
yang
kompleks
dapat
disederhanakan.
Contoh :
Sederhanakan bentuk ~(~p  q)  (p  q)
Penyelesaian :
~(~p  q)  (p  q)
 (~(~p)  ~q)  (p  q)
 (p  ~q)  (p  q)
 p  (~q  q)
pF
p
Jadi
~(~p  q)  (p  q)  p
Dalam membuktikan ekuivalensi P  Q, ada 3 macam cara yang bisa dilakukan :
1. P diturunkan terus menerus (dengan menggunakan hukum-hukum yang ada),
sehingga akhirnya didapat Q
2. Q diturunkan terus menerus (dengan menggunakan hukum-hukum yang ada)
sehingga akhirnya didapat P.
3. P dan Q masing-masing diturunkan secara terpisah ( dengan menggunakan
hukum-hukum yang ada ) sehingga akhirnya sama-sama didapat R
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -6
Sebagai aturan kasar, biasanya bentuk yang lebih kompleks diturunkan ke bentuk
yang lebih sederhana.
Soal Latihan
6. Buktikan ekuivalensi kalimat-kalimat dibawah ini tanpa menggunakan tabel
kebenaran
a. ~(p  ~q) V (~p  ~q)  ~p
b. ~((~p  q)  (~p  ~q) )  (p  q)  p
c. (p  (~(~p  q)))  (p  q)  p
Untuk menunjukkan ekuivalensi 2 kalimat yang melibatkan penghubung

(implikasi) dan  (bi-implikasi), Kita harus terlebih ahulu mengubah penghubung
 dan  menjadi penghubung ,  dan ~. (kenyataan bahwa (p  q)  (~p  q)
mempermudah kita untuk melakukannya)
7. Buktikan ekuivalensi kalimat-kalimat dibawah ini tanpa menggunakan tabel
kebenaran
a. (q  p)  (~p  ~q)
b. (p  (q  r))  ((p  q)  r)
8. Ubahlah bentuk ~(p  q) sehingga hanya memuat penghubung ,  atau ~
1.3 Tautologi dan Kontradiksi
Tautologi adalah suatu bentuk kalimat yang selalu bernilai benar (T), Tidak peduli
bagaimanapun nilai kebenaran masing-masing kalimat penyusunnya. Sebaliknya,
Kontradiksi adalah suatu bentuk kalimat yang selalu bernilai salah (F), tidak peduli
nilai kebenaran masing-masing kalimat penyusunnya.
Dalam tabel kebenaran, suatu Tautologi selalu bernilai T pada semua barisnya, dan
kontradiksi selalu bernilai F pada semua barisnya. Kalau kalimat tautologi
diturunkan lewat hukum-hukum yang ada maka pada akhirnya selalu menghasilkan
T. Sebaliknya , Kontradisi akan selalu menghasilkan F.
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -7
9. Tunjukkan bahwa kalimat-kalimat di bawah ini adalah Tautologi dengan
menggunakan tabel kebenaran.
a. (p  q)  q
b. q  (p  q)
Kesatuan dari 2 buah kalimat ekuivalen p dan q yang dihubungkan dengan
penghubung  selalu merupakan Tautologi karena jika p  q maka p dan q selalu
mempunyai nilai kebenaran yang sama. Jika p dan q mempunyai nilai kebenaran
yang sama, maka p  q selalu akan berniali benar.
10. Tunjukkan bahwa (p  q)  (~q  ~p) berupakan Tautologi, tanpa
menggunakan tabel kebenaran
1.4 Konvers, Invers, dan Kontraposisi
Misal diketahui implikasi
pq
Konvers-nya adalah
qp
Invers-nya adalah
~p  ~q
Kontraposisinya adalah
~q  ~p
Suatu yang penting dalam logika adalah kenyataan bahwa suatu implikasi selalu
ekuivalen dengan konraposisinya. Akan tetapi, tidak demikian dengan Invers dan
konvers. Suatu implikasi tidak selalu ekuivalen dengan Invers ataupun Konvers-nya.
Hal ini dapat dilihat pada tabel kebenaran yang tampak pada pada tabel berikut :
p
q
~p
~q
pq
qp
~p  ~q
~q  ~p
T
T
F
F
T
T
T
T
T
F
F
T
F
T
T
F
F
T
T
F
T
F
F
T
F
F
T
T
T
T
T
T
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -8
Dalam tabel terlihat bahwa nilai kebenaran kolom p  q selalu sama dengan nilai
kebenaran kolom ~q  ~p (Kontraposisi), tetapi tidak selalu sama dengan kolom q
 p (konvers) maupun kolom ~p  ~q (invers).
Disimpulkan bahwa (p  q)  (~q  ~p) merupakan suatu Tautologi.
11. Apakah Konvers, invers, dan Kontraposisi kalimat dibawah ini :
a. Jika A merpakan suatu bujursangkar, maka A merupakan suatu persegi
panjang.
b. Jika n adalah bilangan prima > 2, maka n adalah bilangan ganjil
1.5 Inferensi Logika
Logika selalu berhubungan dengan pernyataan-pernyataan yang ditentukan nilai
kebenarannya. Sering kali diinginkan untuk menentukan benar tidaknya kesimpulan
berdasarkan sejumlah kalimat yang diketahui nilai kebenarannya.Argumen Valid
dan Invalid
Argumen adalah rangkaian kalimat-kalimat. Semua kalimat-kalimat tersebut kecuali
yang terakhir disebut Hipotesa (atau assumsi/premise). Kalimat terakhir disebut
kesimpulan.
Secara umum, hipotesa dan kesimpulan dapat digambarkan sebagai berikut :
p1
p2
}
hipotesa
…….
pn
q
} kesimpulan
(tanda  q dibaca “ jadi q”)
Suatu Argumen dikatakan Valid apabila untuk sembarang pernyataan yang disu yang
disubstitusikan ke dalam hipotesa, jika semua hipotesa tersebut benar, maka
kesimpulan juga benar. Sebaliknya, meskipun semua hipotesa benar tetapi ada
kesimpulan yang salah, maka argumen tersebut dikatakan Invalid.
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -9
Kalau suatu argumen dan semua hipotesanya bernilai benar, maka kebenaran nilai
konklusi dikatakan sebagai “diinfernsikan” (diturunkan) dari kebenaran hipotesa”
Untuk mengecek apakah suatu argumen merupakan kalimat yang valid, dapat
dilakukan langkah-langkah sebagai berikut :
1. Tentukan hipotesa dan kesimpulan kalimat
2. Buat tabel yang menunjukkan nilai kebenaran untuk semua hipotesa dan
kesimpulan.
3. Carilah baris kritis, yaitu baris dimana semua hipotesa bernilai benar.
4. Dalam Baris kritis tersebut, jika semua nilai kesimpulan benar, maka argumen itu
valid. Jika diantara baris kritis tersebut ada baris dengan nilai kesimpulan yang
salah, maka argumen tersebut invalid.
Contoh :
Tentukan apakah Argumen di bawah ini Valid/Invalid.
a.
p  (q  r)
b.
p  (q  ~r)
~r
q  (p  r)
--------------
----------------
pq
p r
Penyelesaian :
a. Ada 2 Hipotesa, masing-masing p  (q  r) dan ~ r. Kesimpulannya adalah p  q.
Tabel kebenaran hipotesa-hipotesa dan kesimpulan adalah sbb :
p
q
r
qr
p  (q  r)
~r
pq
1.
T
T
T
T
T
F
T
2. *
T
T
F
T
T
T
T
3.
T
F
T
T
T
F
T
4. *
T
F
F
F
T
T
T
5.
F
T
T
T
T
F
T
6. *
F
T
F
T
T
T
T
7.
F
F
T
T
T
F
F
8.
F
F
F
F
F
T
F
Baris ke
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -10
Baris Kritis adalah baris 2, 4, dan 6 (baris yang semua hipotesanya bernilai T ). Pada
baris-baris tersebut kesimpulannya juga bernilai T. Maka argumen tersebut bernilai
valid.
b. silahkan anda coba sendiri.
1.5.1 Metode-Metode Inferensi
Pada bagian ini dipelajari beberapa metode infernsi, yaitu teknik untuk
menurunkan kesimpulan berdasarkan hipotesayang ada, tanpa harus menggunakan
tabel kebenaran.
1. Modus Ponens
Perhatikan implikasi “ bila p maka q “ yang diasumsikan bernilai benar.
Apabila selanjutnya diketahui bahwa anteseden (p) benar, supaya implikasi p
 q benar, maka q juga harus bernilai benar. Infersi seperti itu disebut Modus
Ponens.
Secara simbolik, Modus Ponens dapat dinyatakan sbb :
pq
p
--------q
Hal ini dapat dilihat dari tabel kebenaran yang tampak pada tabel berikut.
Baris ke
1. *
2.
3.
4.
p
T
T
F
F
q
T
F
T
F
pq
T
F
T
T
p
T
T
F
F
q
T
F
T
F
Baris Kritis adalah baris pertama. Pada baris tersebut, konklusi (q) bernilai T
sehingga argumennya valid.
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -11
2. Modsus Tollens
Bentuk Modus Tollens mirip dengan Modus Pones, hanya saja hipotesa
kedua dan kesimpulan merupakan kontraposisi hipotesa pertama modus
ponens. Hal ini mengingat kenyataan bahwa suatu implikasi selalu
ekuivalen dengan kontraposisinya.
Secara simbolik, bentuk inferensi Modus Tollens adalah sebagai berikut :
pq
~q
-------- ~p
Contoh:
Jika Zeus seorang manusia, maka ia dapat mati
Zeus tidak dapat mati
-------------------------------------------------------- Zeus bukan seorang manusia.
3. Penambahan Disjungtif
Inferensi Penambahan Disjungtif didasarkan atas fakta bahwa suatu
kalimat dapat digeneralisasikan dengan penghubung “  ”. Alasannya
adalah karena penghubung “  “ bernilai benar jika salah satu
komponennya bernilai benar.
Sebagai contoh : “Ani suka jeruk” (bernilai benar). Kalimat tersebut tetap
bernilai benar jika ditambahkan kalimat lain dengan penghubung “  ”.
Jadi kalimat “Ani suka jeruk atau apel” juga tetap bernilai benar dan tidak
tergantung pa suka/tidaknya Ani akan apel.
Bentuk Simbolis metode Infernsi Penambahan Disjungtif adalah sebagai
berikut :
p
a.
---------p  q
STMIK ‘Sinus’ Ska
q
b.
---------pq
Wawan Laksito YS
Logika Informatika -12
4. Penyderhanaan Konjungtif
Inferensi penyederhanaan Konjungtif merupakan kebalikan dari inferensi
Penambahan Disjungtif. Jika beberapa kalimat dihubungkan dengan
penghubung ”  “, kalimat tersebut dapat diambil salah satunya secara
Khusus. Penyempitan kalimat ini merupakan kebalikan dari penambahan
Disjungtif yang merupakan perluasan kalimat.
Bentuk simbolis metode Inferensi penyederhanaan Konjungtif adalah sbb :
pq
---------b.
p
Contoh :
Lina menguasai bahasa Basic dan Pascal
------------------------------------------------ Lina mengusai bahasa Basic
a.
pq
--------- q
5. Silogisme Disjungtif
Prinsip dasar Silogisme Disjungtif adalah kenyataan bahwa apabila kita
diperhadapkan pada satu diantara 2 pilihan yang ditawarkan (A atau B),
sedangkan kita tidak memilih A, Maka satu-satunya pilihan yang mungkin
adalah memilih B. Hal ini sering dijumpai dalam kehidupan sehar-hari.
Jika seseorang ditanyai oleh penjual warung : “ Kamu minum es jeruk atau
es the?”. Dan orang yang ditanya tersebut harus memilih salah satu,
sedangkan ia tidak suka es jeruk, pastilah ia memilih es teh.
Secara simbolis, bentuk metode inferensi Silogisme Disjungtif adalah
sebagai berikut :
a.
pq
~p
---------q
b.
pq
~q
----------p
Contoh :
Kunci kamarku ada di sakuku atau tertinggal di rumah
Kunci kamarku tidak ada di sakuku
---------------------------------------------------------------- Kunci kamarku tertinggal di rumah
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -13
6. Silogisme Hipotesis
Prinsip Silogisme Hipotesis adalah sifat transitif pada implikasi. Jika
implikasi p  q dan q  r keduanya bernilai benar, maka implikasi p  r
bernilai benar pula.
Secara simbolis, bentuk metode inferensi Silogisme Hipotesis adalah sbb :
pq
qr
---------pr
Contoh :
Jika 18486 habis dibagi 18, maka 18486 habis dibagi 9
Jika 18486 habis dibagi 9, maka jumlah digit-digitnya habis dibagi 3
---------------------------------------------------------------------------------- 18486 habis dibagi 18, maka jumlah digit-digitnya habis dibagi 9.
7. Dilema (Pembagian Dalam Beberapa Kasus)
Kadeng-kadang, dalam kalimat yang dihubungkan dengan penghubung “
 “, Masing-masing kalimat dapat mengimplikasikan sesuatu yang sama.
Berdasrkan hal itu maka suatu kesimpulan dapat diambil.
Secara simbolis, bentuk metode infernsi Dilema adalah sebahgai berikut :
pq
pr
qr
--------r
Contoh :
Nanti malam Adi mengajak saya nonton atau mengajak saya makan di
restoran
Jika Adi mengajak saya nonton, maka saya akan senang
Jika Adi mengajak saya makan di restoran, maka saya akan senang
--------------------------------------------------------------------------------Nanti malam saya akan senang
STMIK ‘Sinus’ Ska
Wawan Laksito YS
Logika Informatika -14
8. Konjungsi
Inferensi Konjungsi sebenarnya sudah dibahas pada sub-bab awal. Jika ada
dua kalimat yang masing-masing benar, maka gabungan kedua kalimat
tersebut dengan menggunakan ““ (konjungsi) juga bernilai benar.
Bentuk Inferensi dengan Konjungsi adalah sbb :
p
q
-----------pq
Kedelapan bentuk infernsi dapat dirngkas pada tabel berikut :
Aturan
Bentuk Argumen
pq
p
--------q
Modus Ponen
pq
~q
-------- ~p
Modus Tollen
Penambahan Disjungtif
Penyederhanaan Konjungtif
Silogisme Disjungtif
Silogisme Hipotesis
Dilema
Konjungsi
STMIK ‘Sinus’ Ska
p
-------pq
pq
-----p
pq
~p
------q
q
-------pq
pq
-----q
pq
~q
------p
pq
qr
-------r
Pq
pr
qr
-------r
p
q
-------pq
Wawan Laksito YS
Logika Informatika -15
Soal latihan :
12. Pada suatu hari, Anda hendak pergi ke kampus dan baru sadar bahwa Anda tidak
memakai kacamata. Setelah mengingat-ingat, ada beberapa fakta yang Anda pastikan
kebenaranya :
a. Jika kacamataku ada di meja dapur, maka aku pasti sudah melihatnya ketika
sarapan pagi.
b. Aku membaca koran di ruang tamu atau akau membacanya di dapur.
c. Jika aku membaca koran di ruang tamu, maka pastilah kacamataku kuletakkan di
meja tamu.
d. Aku tidak melihat kacamataku pada waktu sarapan pagi
e. Jika aku membaca buku di ranjang, maka kacamata kuletakkan di meja samping
ranjang.
f. Jika aku membaca koran di dapur, maka kacamataku ada di meja dapur.
Berdasarkan fakta-fakta tersebut, tentukan dimana letak kacamata tersebut!
13. Buktikan Kevaidan Argumen di bawah ini dengan menggunakan prinsip=prinsip
infernsi Logika.
p q
(p  q)  r
-----------------
r
STMIK ‘Sinus’ Ska
Wawan Laksito YS